Chaque développeur Android a utilisé RecyclerView pour afficher les listes, et chacun a été confronté au problème de mise à jour des données de la liste jusqu'à l' DiffUtil la classe magique DiffUtil en 2016. Je vais expliquer aux doigts comment cela fonctionne réellement et essayer de dissiper sa magie.
Un peu d'histoire
L'un des éléments les plus courants dans les applications mobiles est la liste, dans notre cas RecyclerView . Il peut s'agir de listes de n'importe quoi: adresses de bureaux, listes d'amis sur les réseaux sociaux. réseaux, historique des commandes dans les applications de taxi, etc. Tous ces cas sont unis par la nécessité de changer constamment les données de la liste en nouvelles, lorsque, par exemple, l'utilisateur a fait glisser pour actualiser, filtré la liste ou reçu de toute autre manière un pack de nouvelles données à l'arrière.
Pour implémenter ce comportement, l'ancêtre du développeur Android moderne a sélectionné manuellement les données et la façon dont elles ont changé, et a appelé les méthodes appropriées à partir de RecyclerView . Cependant, tout a changé lorsque Google a publié la version 25.1.0 de la bibliothèque de support, y ajoutant DiffUtil , ce qui vous a permis de transformer comme par magie l'ancienne liste en une nouvelle sans reconstruire complètement RecyclerView . Dans cet article, je vais dissiper la magie de DiffUtil et expliquer comment cela fonctionne.
Comment travailler avec DiffUtil?
Pour travailler avec DiffUtil vous devez implémenter DiffUtil.Callback , appeler la méthode calculateDiff(@NonNull Callback cb) et appliquer le DiffResult reçu au RecyclerView à l'aide de la méthode dispatchUpdatesTo() . Que se passe-t-il lorsque la calucalteDiff(@NonNull Callback cd) est appelée? Cette méthode renvoie un DiffResult , qui contient un ensemble d'opérations pour convertir la liste d'origine en une nouvelle. Les mises à jour sont appliquées par des appels aux notifyItemRangeInserted , notifyItemRangeRemoved , notifyItemMoved et notifyItemRangeChanged . Les trois premières méthodes modifient la structure de la liste, à savoir les positions des éléments, sans modifier les éléments eux-mêmes et sans appeler onBindViewHolder() sur eux (à l'exception de l'élément ajouté). Ce dernier modifie l'élément lui-même et appelle onBindViewHolder() pour changer la vue de l'élément.
DiffUtil vérifie les deux listes pour les différences en utilisant l'algorithme Myers, qui détermine uniquement la présence / absence de changements, mais ne sait pas comment trouver le mouvement des éléments. Pour ce faire, DiffUtil parcourt les DiffUtil créés par l'algorithme de Myers (plus à ce sujet plus tard), puis recherche les mouvements. DiffResult est formé pour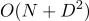 
si l'algorithme ne vérifie pas le mouvement des éléments et 
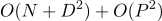, où P est le nombre d'éléments ajoutés et supprimés.
Algorithme Myers
Ensuite, une explication de l'algorithme Myers sur les doigts sera considérée, des liens vers des explications mathématiques de l'algorithme (ainsi que d'autres articles sympas sur le sujet) seront à la fin de l'article. Considérons deux séquences: BACAAC et CBCBAB. Il est nécessaire d'écrire une séquence de transformations sur la première séquence, après quoi nous obtenons la seconde. Nous écrivons les séquences dans le tableau comme suit: l'ancienne liste désignera les premiers éléments des colonnes, et la nouvelle liste sera les premiers éléments des lignes.
Rayer les cellules dans lesquelles des éléments identiques des deux séquences se croisent:
Une autre tâche consiste à passer du coin supérieur gauche de la matrice au coin inférieur droit en un minimum d'étapes. Vous pouvez vous déplacer le long des faces horizontales et verticales. Si vous atteignez le point de départ de la ligne diagonale, vous devez vous déplacer le long de celle-ci, mais le coût d'une telle étape est de 0. Par conséquent, le coût d'une étape le long des bords est de 1.
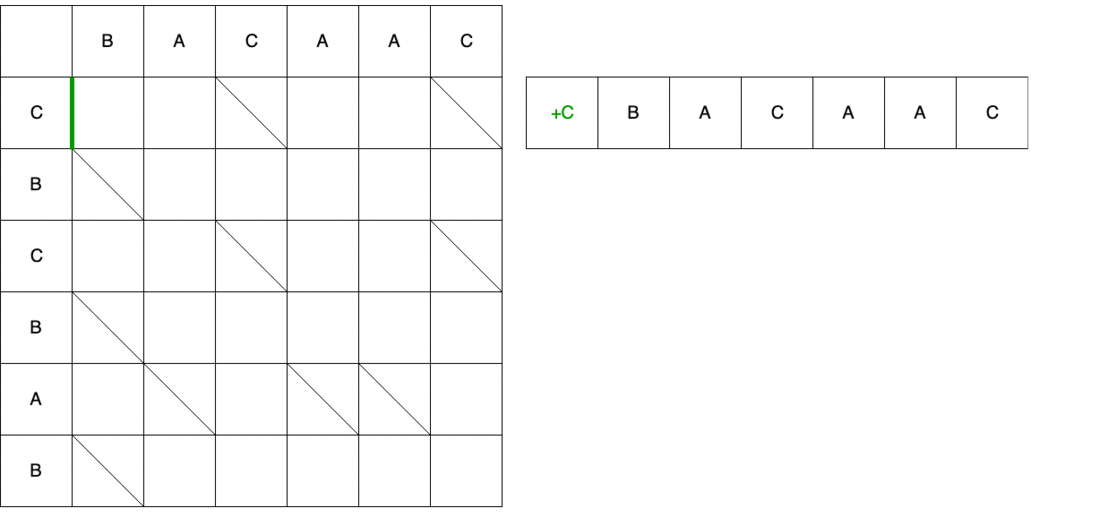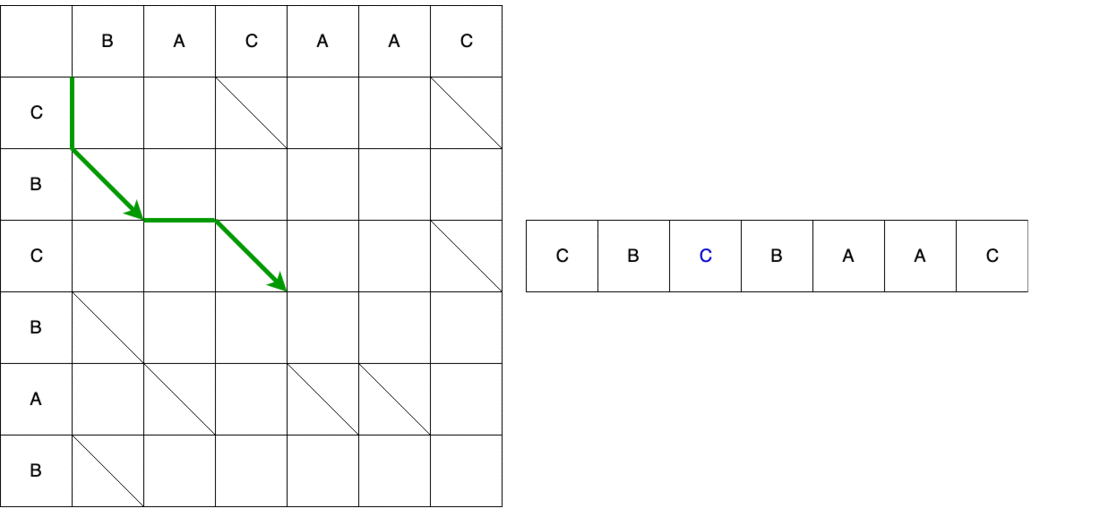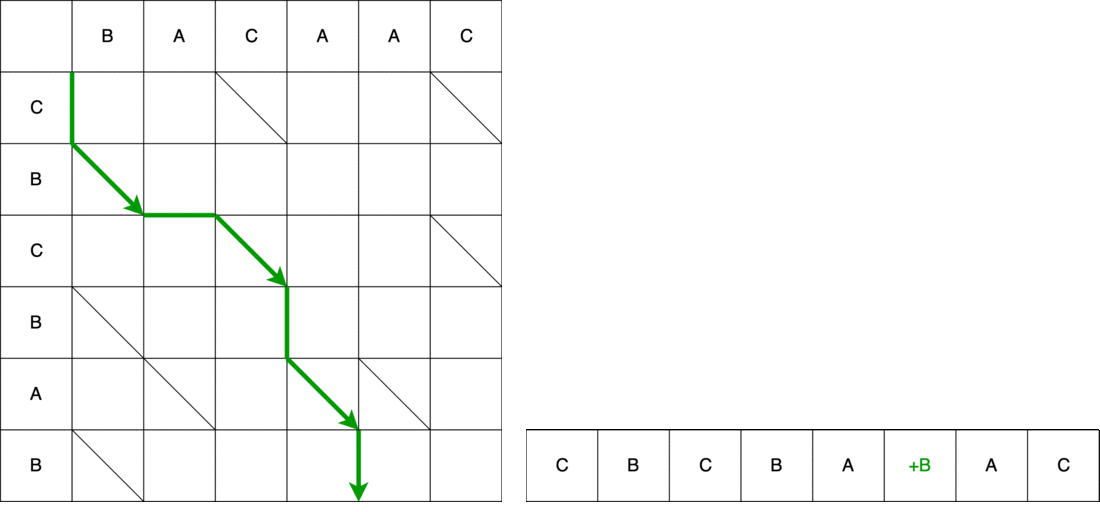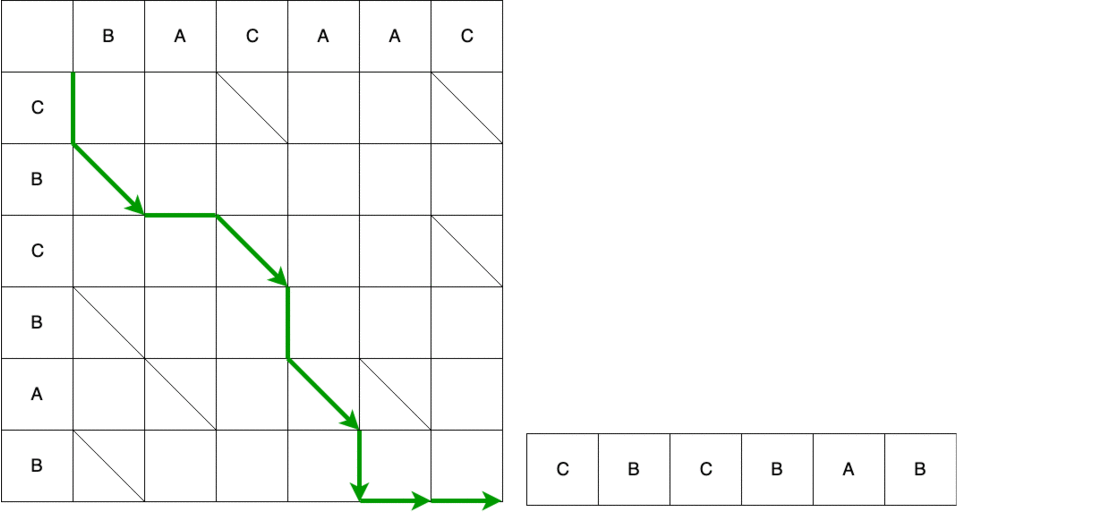
À partir du point (0; 0), nous pouvons nous déplacer vers la droite et vers le bas. Lorsque vous descendez, vous devez en outre aller en diagonale. Le mouvement effectué en une étape est appelé serpent, dans ce cas 2 serpents reçus: (0; 0) -> (0; 1) et (0; 0) -> (1; 2). La flèche indique la fin du serpent, c'est-à-dire si après l'étape verticale / horizontale il y a une étape obligatoire le long de la diagonale, alors la flèche sera sur l'étape le long de la diagonale. La construction complète des serpents du point de départ à la finale est illustrée ci-dessous. Certains chemins sur la vidéo ont été omis car n'étaient évidemment pas les plus courts.
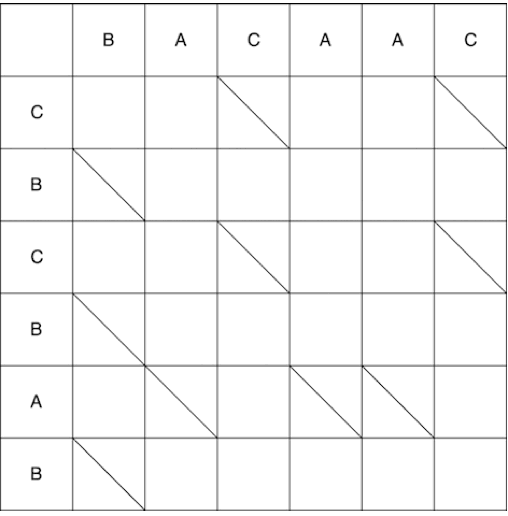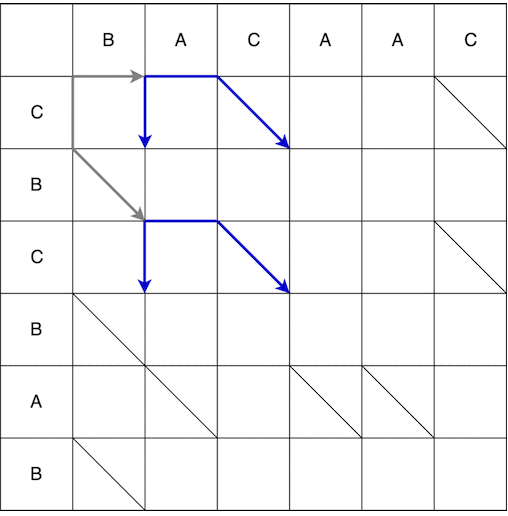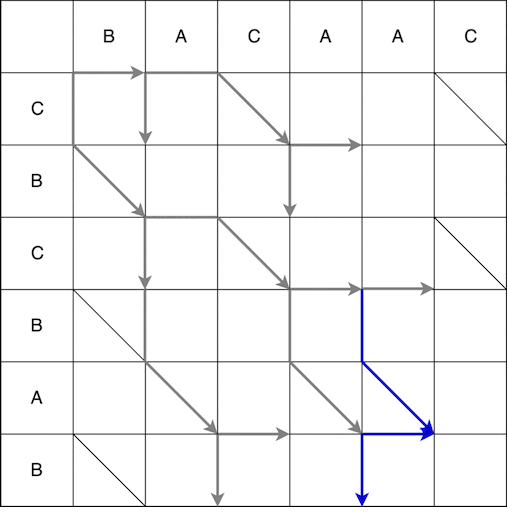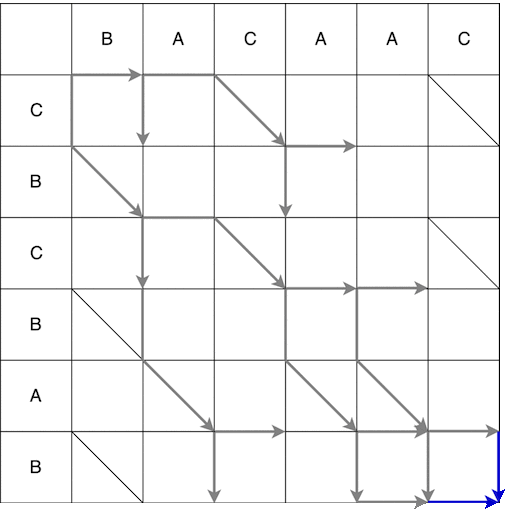
En conséquence, nous obtenons plusieurs chemins les plus courts possibles, certains d'entre eux sont affichés ci-dessous.
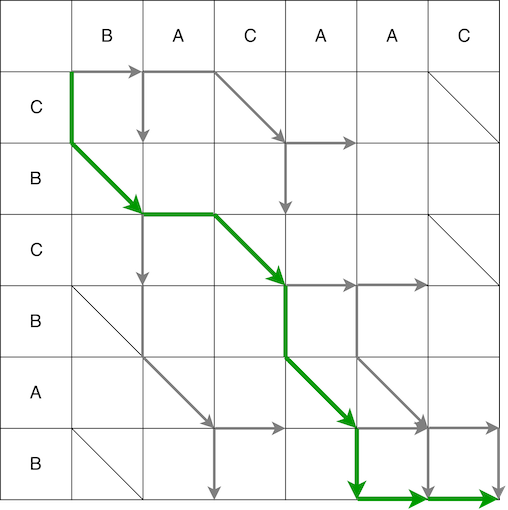
Comment le passage d'une matrice de l'extrême gauche à l'extrême droite peut-il déterminer la séquence d'actions (script) pour convertir une séquence en une autre? Que signifient les pas horizontaux, verticaux et diagonaux? Une étape le long de la matrice dans l'une des directions possibles est les actions sur l'ancienne ligne:
- Étape horizontale - supprimer de l'ancienne ligne
- Étape verticale - Ajouter à l'ancienne ligne
- Marche diagonale - pas de changement
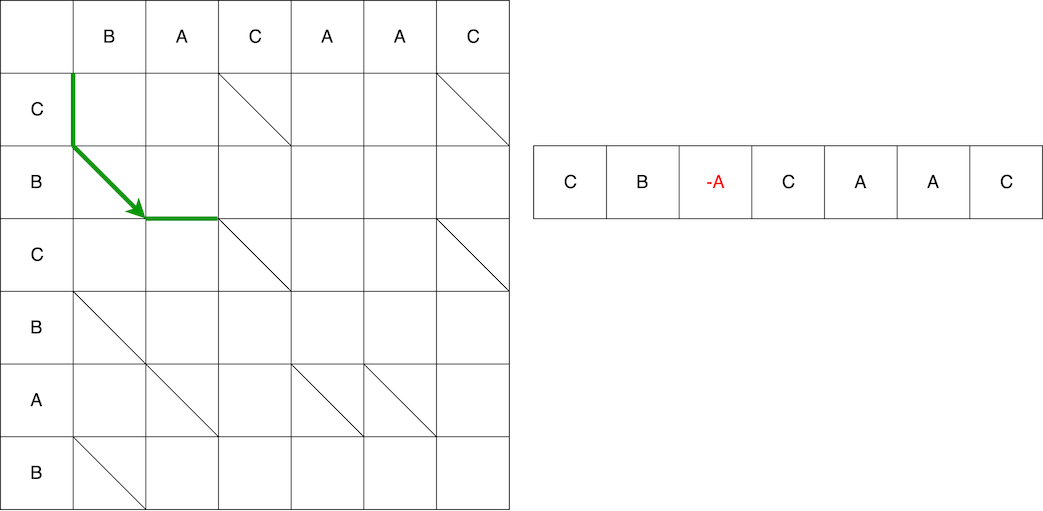
En utilisant le deuxième chemin comme exemple, nous comparons le chemin et le script résultant. La première étape est verticale, ce qui signifie que nous ajoutons le caractère «C» à la position 0 dans l'ancienne ligne.
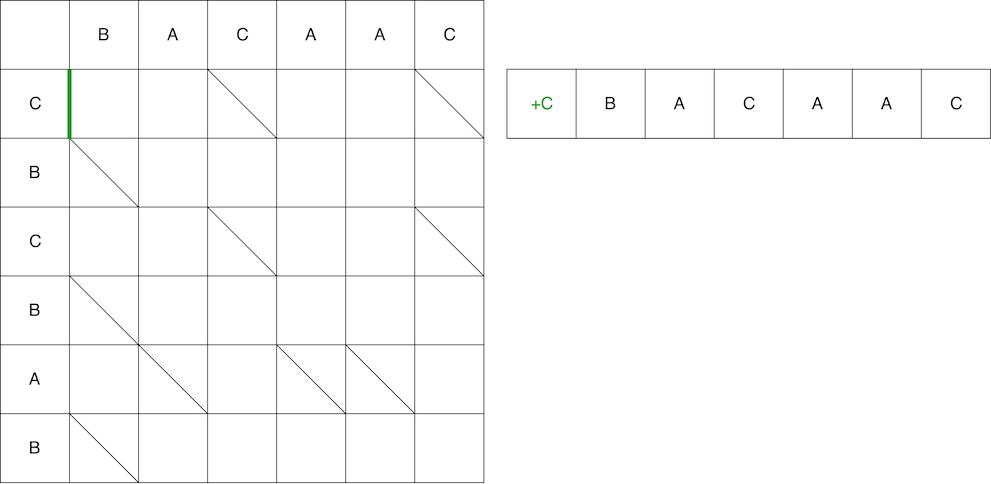
Cependant, ce n'est pas le serpent entier. Ensuite, nous devons nous déplacer en diagonale. Lors d'un déplacement en diagonale, l'élément B reste inchangé. En conséquence, le serpent se compose d'un mouvement vertical + d'un mouvement diagonal.
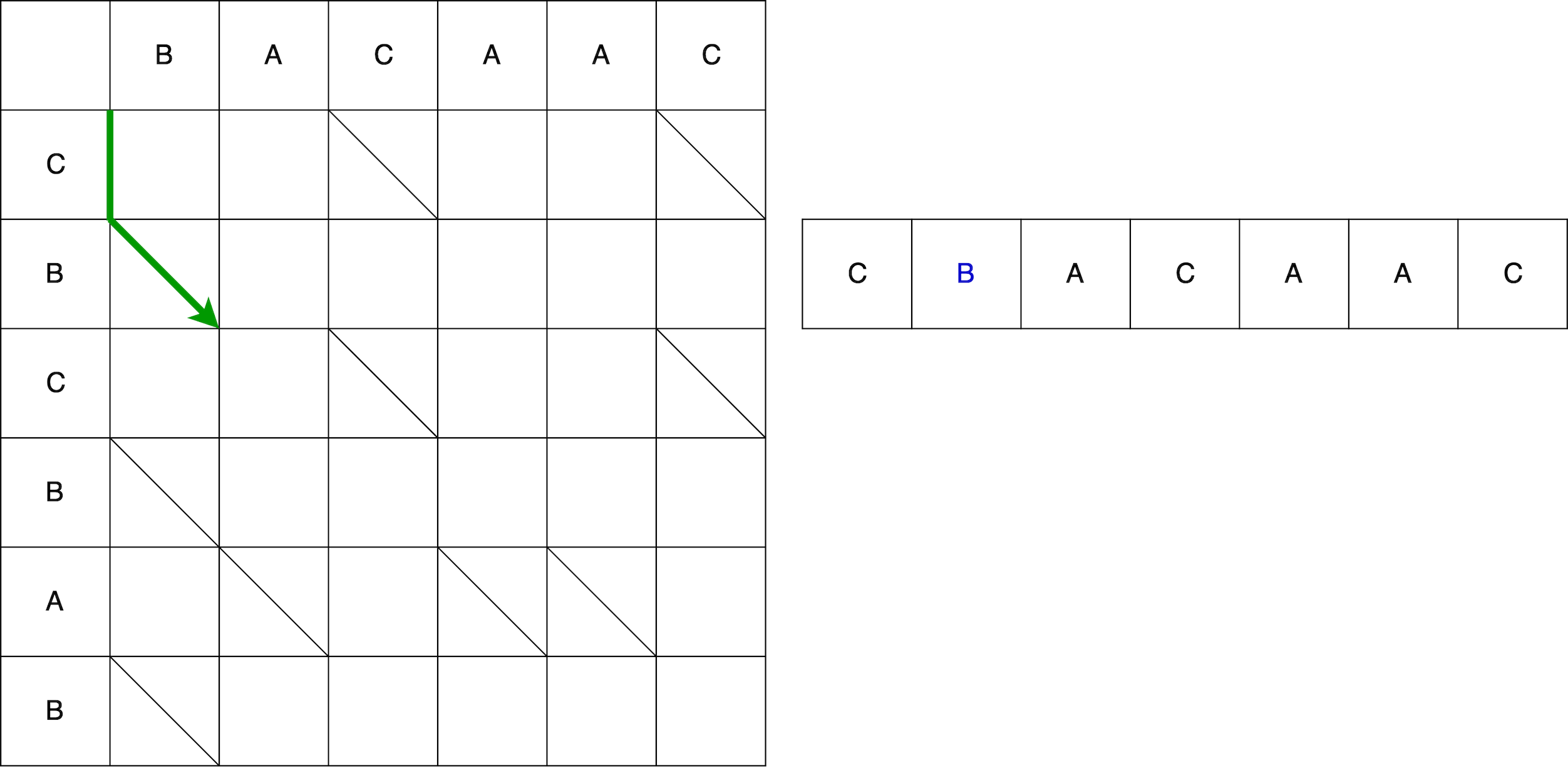
Ensuite, le serpent horizontalement - retirez l'élément A. de l'ancienne ligne
La vidéo montre le chemin complet du début à la fin avec un changement dans la chaîne source jusqu'à ce qu'il soit converti en le dernier.
Le résultat de l'algorithme Myers est un script avec un ensemble du nombre minimum d'actions qui doivent être effectuées pour convertir une séquence en une autre. Dans DiffUtil l'algorithme Myers est utilisé pour rechercher différents éléments qui sont déterminés par la méthode areItemsTheSame() . En plus de former une liste de serpents, en passant par des listes, l'algorithme Myers crée des listes de statuts d'éléments des anciennes et nouvelles listes. Toutes ces données, ainsi que l'indicateur detectMoves et le rappel implémenté par l'utilisateur, sont passés au constructeur DiffResult(Callback callback, List<Snake> snakes, int[] oldItemStatuses, int[] newItemStatuses, boolean detectMoves) .
Pendant que j'écrivais cet article, j'ai pu découvrir ce qui se passe exactement dans DiffResult : l'algorithme passe par les serpents et définit des drapeaux aux éléments (dans les listes d'état), ce qui détermine ce qui est exactement arrivé à l'élément. À l'aide de ces indicateurs, lors de l'application de modifications à RecyclerView est déterminé à quelle méthode appliquer les mises à jour: notifyItemRangeInserted, notifyItemRangeRemoved, notifyItemMoved notifyItemRangeChanged . Plus en détail, j'en parlerai la prochaine fois.
Les références