Réseaux de neurones et apprentissage profond, chapitre 3, partie 3: comment choisir les hyperparamètres de réseaux de neurones?

Jusqu'à présent, je n'ai pas expliqué comment je choisis les valeurs des hyperparamètres - le taux d'apprentissage η, le paramètre de régularisation λ, etc. Je viens de donner de belles valeurs de travail. En pratique, lorsque vous utilisez un réseau neuronal pour attaquer un problème, il peut être difficile de trouver de bons hyperparamètres. Imaginez, par exemple, qu'on vient de nous parler du problème MNIST, et que nous avons commencé à travailler dessus, sans rien savoir des valeurs des hyperparamètres appropriés. Supposons que nous ayons eu de la chance par hasard, et dans les premières expériences, nous avons choisi de nombreux hyperparamètres comme nous l'avons déjà fait dans ce chapitre: 30 neurones cachés, une taille de mini-paquet de 10, une formation de 30 époques et l'utilisation de l'entropie croisée. Cependant, nous avons choisi le taux d'apprentissage η = 10,0 et le paramètre de régularisation λ = 1000,0. Et voici ce que j'ai vu avec une telle course:

>>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10]) >>> net.SGD(training_data, 30, 10, 10.0, lmbda = 1000.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 1030 / 10000 Epoch 1 training complete Accuracy on evaluation data: 990 / 10000 Epoch 2 training complete Accuracy on evaluation data: 1009 / 10000 ... Epoch 27 training complete Accuracy on evaluation data: 1009 / 10000 Epoch 28 training complete Accuracy on evaluation data: 983 / 10000 Epoch 29 training complete Accuracy on evaluation data: 967 / 10000 

Notre classification ne fonctionne pas mieux que l'échantillonnage aléatoire! Notre réseau fonctionne comme un générateur de bruit aléatoire!

"Eh bien, c'est facile à résoudre", pourrait-on dire, "il suffit de réduire les hyperparamètres tels que la vitesse d'apprentissage et la régularisation". Malheureusement, a priori, vous n'avez pas d'informations sur ce que ces hyperparamètres doivent être ajustés. Peut-être que le principal problème est que nos 30 neurones cachés ne fonctionneront jamais, quelle que soit la façon dont les autres hyperparamètres sont sélectionnés? Peut-être avons-nous besoin d'au moins 100 neurones cachés? Ou 300? Ou beaucoup de couches cachées? Ou une approche différente du codage de sortie? Peut-être que notre réseau apprend, mais que nous devons le former à plusieurs époques? Peut-être que la taille des mini-paquets est trop petite? Peut-être aurions-nous mieux fait si nous étions revenus à la fonction quadratique de la valeur? Peut-être que nous devons essayer une approche différente pour initialiser les poids? Et ainsi de suite et ainsi de suite. Dans l'espace des hyperparamètres, il est facile de se perdre. Et cela peut vraiment entraîner beaucoup d'inconvénients si votre réseau est très grand ou utilise d'énormes quantités de données de formation, et vous pouvez les entraîner pendant des heures, des jours ou des semaines sans recevoir de résultats. Dans une telle situation, votre confiance commence à passer. Peut-être que les réseaux de neurones n'étaient pas la bonne approche pour résoudre votre problème? Peut-être que vous quittez et faites l'apiculture?

Dans cette section, je vais expliquer quelques approches heuristiques que vous pouvez utiliser pour configurer des hyperparamètres dans un réseau neuronal. L'objectif est de vous aider à élaborer un workflow qui vous permet de configurer assez bien les hyperparamètres. Bien sûr, je ne peux pas couvrir tout le sujet de l'optimisation hyperparamétrique. C'est un domaine immense, et ce n'est pas un problème qui peut être résolu complètement, ou selon les stratégies correctes de résolution qui font l'unanimité. Il y a toujours la possibilité d'essayer une autre astuce pour extraire des résultats supplémentaires de votre réseau neuronal. Mais l'heuristique de cette section devrait vous donner un point de départ.

Stratégie générale

Lors de l'utilisation d'un réseau neuronal pour attaquer un nouveau problème, la première difficulté est d'obtenir des résultats non triviaux du réseau, c'est-à-dire de dépasser une probabilité aléatoire. Cela peut être étonnamment difficile, surtout lorsque vous êtes confronté à une nouvelle classe de tâches. Examinons quelques stratégies qui peuvent être utilisées pour ce type de difficulté.

Supposons, par exemple, que vous soyez le premier à attaquer la tâche MNIST. Vous commencez avec beaucoup d'enthousiasme, mais l'échec complet de votre premier réseau est un peu décourageant, comme décrit dans l'exemple ci-dessus. Ensuite, vous devez démonter le problème en plusieurs parties. Vous devez vous débarrasser de toutes les images d'entraînement et de support, à l'exception des images de zéros et de uns. Ensuite, essayez de former le réseau pour distinguer 0 de 1. Cette tâche est non seulement essentiellement plus facile que de distinguer les dix chiffres, elle réduit également la quantité de données d'entraînement de 80%, accélérant ainsi l'apprentissage de 5 fois. Cela vous permet de mener des expériences beaucoup plus rapidement et vous donne la possibilité de comprendre rapidement comment créer un bon réseau.

Les expériences peuvent être encore accélérées en réduisant le réseau à une taille minimale susceptible d'être correctement formée. Si vous pensez que le réseau [784, 10] est très susceptible de classer les chiffres du MNIST mieux qu'un échantillon aléatoire, alors commencez à l'expérimenter. Ce sera beaucoup plus rapide que l'entraînement [784, 30, 10], et vous pouvez déjà y arriver plus tard.

Une autre accélération des expériences peut être obtenue en augmentant la fréquence de suivi. Dans le programme network2.py, nous surveillons la qualité du travail à la fin de chaque ère. En traitant 50 000 images par époque, nous devons attendre assez longtemps - environ 10 secondes par époque sur mon ordinateur portable pendant la formation réseau [784, 30, 10] - avant d'obtenir des commentaires sur la qualité de la formation réseau. Bien sûr, dix secondes, ce n'est pas si long, mais si vous voulez essayer quelques dizaines d'hyperparamètres différents, cela commence à ennuyer, et si vous voulez essayer des centaines ou des milliers d'options, cela dévaste simplement. Les commentaires peuvent être reçus beaucoup plus rapidement en suivant plus souvent la précision de la confirmation, par exemple, toutes les 1000 images d'entraînement. De plus, au lieu d'utiliser l'ensemble complet de 10 000 images de confirmation, nous pouvons obtenir une estimation beaucoup plus rapidement en utilisant seulement 100 images de confirmation. L'essentiel est que le réseau voit suffisamment d'images pour vraiment apprendre et pour obtenir une estimation suffisamment bonne de l'efficacité. Bien sûr, notre network2.py ne fournit pas encore ce suivi. Mais en tant que béquilles pour obtenir cet effet à des fins d'illustration, nous recadrons nos données d'entraînement aux 1000 premières images MNIST. Essayons de voir ce qui se passe (pour la simplicité du code, je n'ai pas utilisé l'idée de ne laisser que les images 0 et 1 - cela peut aussi être réalisé avec un peu plus d'effort).

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 1000.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 10 / 100 Epoch 1 training complete Accuracy on evaluation data: 10 / 100 Epoch 2 training complete Accuracy on evaluation data: 10 / 100 ... 

Nous obtenons toujours du bruit pur, mais nous avons un gros avantage: le feedback est mis à jour en quelques fractions de seconde, et pas toutes les dix secondes. Cela signifie que vous pouvez expérimenter beaucoup plus rapidement avec la sélection d'hyperparamètres, ou même expérimenter avec de nombreux hyperparamètres différents presque simultanément.

Dans l'exemple ci-dessus, j'ai laissé la valeur de λ égale à 1000,0, comme précédemment. Mais puisque nous avons changé le nombre d'exemples d'entraînement, nous devons changer λ de sorte que l'affaiblissement des poids soit le même. Cela signifie que nous changeons λ de 20,0. Dans ce cas, les éléments suivants se révéleront:

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 12 / 100 Epoch 1 training complete Accuracy on evaluation data: 14 / 100 Epoch 2 training complete Accuracy on evaluation data: 25 / 100 Epoch 3 training complete Accuracy on evaluation data: 18 / 100 ... 

Ouais! Nous avons un signal. Pas particulièrement bon, mais il y en a. Cela peut déjà être pris comme point de départ et modifier les hyperparamètres pour essayer d'obtenir de nouvelles améliorations. Supposons que nous décidions que nous devons augmenter la vitesse d'apprentissage (comme vous l'avez probablement compris, nous avons décidé incorrectement, pour la raison que nous discuterons plus tard, mais essayons de le faire pour l'instant). Pour tester notre supposition, nous tournons η à 100,0:

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 100.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 10 / 100 Epoch 1 training complete Accuracy on evaluation data: 10 / 100 Epoch 2 training complete Accuracy on evaluation data: 10 / 100 Epoch 3 training complete Accuracy on evaluation data: 10 / 100 ... 

Tout va mal! Apparemment, notre supposition était incorrecte et le problème n'était pas dans la très faible valeur de la vitesse d'apprentissage. Nous essayons de resserrer η à une petite valeur de 1,0:

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 1.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 62 / 100 Epoch 1 training complete Accuracy on evaluation data: 42 / 100 Epoch 2 training complete Accuracy on evaluation data: 43 / 100 Epoch 3 training complete Accuracy on evaluation data: 61 / 100 ... 

C'est mieux! Et ainsi nous pouvons continuer plus loin, en tordant chaque hyperparamètre et en améliorant progressivement l'efficacité. Après avoir étudié la situation et trouvé une valeur améliorée pour η, nous procédons à la recherche d'une bonne valeur pour λ. Ensuite, nous allons mener une expérience avec une architecture plus complexe, par exemple, avec un réseau de 10 neurones cachés. Ensuite, nous ajustons à nouveau les paramètres pour η et λ. Ensuite, nous augmenterons le réseau à 20 neurones cachés. Un peu de réglage des hyperparamètres. Et ainsi de suite, évaluer l'efficacité à chaque étape en utilisant une partie de nos données de support, et en utilisant ces estimations pour sélectionner tous les meilleurs hyperparamètres. En cours d'améliorations, il faut de plus en plus de temps pour voir l'effet du réglage des hyperparamètres, afin que nous puissions réduire progressivement la fréquence de suivi.

En tant que stratégie globale, cette approche semble prometteuse. Cependant, je veux revenir à cette première étape dans la recherche d'hyperparamètres qui permettent au réseau d'apprendre au moins en quelque sorte. En fait, même dans l'exemple ci-dessus, la situation était trop optimiste. Travailler avec un réseau qui n'apprend rien peut être extrêmement ennuyeux. Vous pouvez ajuster les hyperparamètres pendant plusieurs jours et ne pas recevoir de réponses significatives. Par conséquent, je voudrais souligner une fois de plus que dans les premières étapes, vous devez vous assurer que vous pouvez obtenir un retour rapide des expériences. Intuitivement, il peut sembler que simplifier le problème et l'architecture ne fera que vous ralentir. En fait, cela accélère le processus, car vous pouvez trouver un réseau avec un signal significatif beaucoup plus rapidement. Après avoir reçu un tel signal, vous pourrez souvent obtenir des améliorations rapides lors du réglage des hyperparamètres. Comme dans de nombreuses situations de la vie, le plus difficile est de démarrer le processus.

D'accord, c'est une stratégie générale. Voyons maintenant les recommandations spécifiques pour prescrire des hyperparamètres. Je me concentrerai sur la vitesse d'apprentissage η, le paramètre de régularisation L2 λ et la taille du mini-paquet. Cependant, de nombreux commentaires seront applicables à d'autres hyperparamètres, y compris ceux liés à l'architecture de réseau, à d'autres formes de régularisation et à certains hyperparamètres, que nous apprendrons dans le livre plus tard, par exemple, le coefficient de momentum.

Vitesse d'apprentissage

Supposons que nous ayons lancé trois réseaux MNIST avec trois vitesses d'apprentissage différentes, η = 0,025, η = 0,25 et η = 2,5, respectivement. Nous laisserons le reste des hyperparamètres tels qu'ils étaient dans les sections précédentes - 30 époques, la taille du mini-paquet est de 10, λ = 5,0. Nous reviendrons également sur l'utilisation des 50 000 images d'entraînement. Voici un graphique montrant le comportement du coût de la formation (créé par le programme multiple_eta.py):



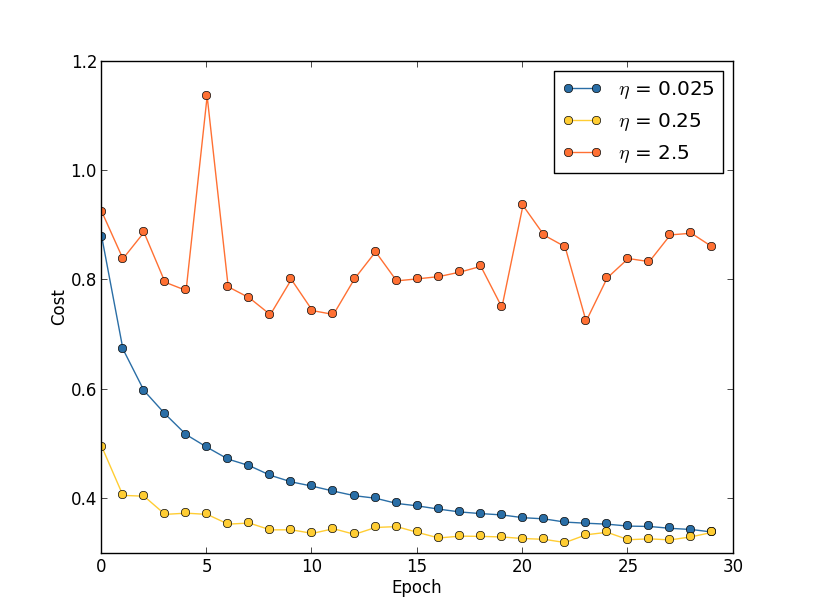
À η = 0,025, le coût diminue en douceur jusqu'à la dernière ère. Avec η = 0,25, le coût diminue initialement, mais après 20 époques, il est saturé, de sorte que la plupart des changements se révèlent être de petites fluctuations et, évidemment, aléatoires. Avec η = 2,5, le coût varie considérablement dès le départ. Pour comprendre la raison de ces fluctuations, nous rappelons que la descente de gradient stochastique devrait progressivement nous abaisser dans la vallée de la fonction de coût:



Cette image aide à imaginer intuitivement ce qui se passe, mais n'est pas une explication complète et complète. Plus précisément, mais brièvement, la descente de gradient utilise une approximation de premier ordre pour la fonction de coût afin de comprendre comment réduire le coût. Pour des η plus grands, les membres d'une fonction de coût d'ordre supérieur deviennent plus importants et ils peuvent dominer le comportement en interrompant la descente de gradient. Cela est particulièrement probable à l'approche des minima et des minima locaux de la fonction de coût, car à côté de ces points, le gradient devient petit, ce qui facilite la domination des membres d'un ordre supérieur.

Cependant, si η est trop grand, alors les marches seront si grandes qu'elles pourront sauter un minimum, grâce à quoi l'algorithme grimpera de la vallée. C'est probablement ce qui fait osciller le prix à η = 2,5. Le choix de η = 0,25 conduit au fait que les étapes initiales nous conduisent vraiment vers un minimum de la fonction de coût, et ce n'est que lorsque nous y arrivons que nous commençons à éprouver des difficultés à sauter. Et lorsque nous choisissons η = 0,025, nous n’avons pas de telles difficultés au cours des 30 premières époques. Bien sûr, le choix d'une si petite valeur de η crée une autre difficulté - à savoir, il ralentit la descente du gradient stochastique. La meilleure approche serait de commencer avec η = 0,25, d'apprendre 20 époques, puis de passer à η = 0,025. Plus tard, nous discuterons d'un tel taux d'apprentissage variable. En attendant, arrêtons-nous sur la question de trouver une valeur appropriée pour la vitesse d'apprentissage η.

Dans cet esprit, nous pouvons choisir η comme suit. Premièrement, nous évaluons la valeur seuil η à laquelle le coût des données de formation commence immédiatement à diminuer, mais ne fluctue pas et n'augmente pas. Cette estimation n'a pas besoin d'être exacte. L'ordre peut être estimé en commençant par η = 0,01. Si le coût diminue au cours des premières époques, il vaut la peine d'essayer η = 0,1, puis 1,0, et ainsi de suite, jusqu'à ce que vous trouviez une valeur à laquelle la valeur fluctue ou augmente au cours des premières époques. Et vice versa, si la valeur fluctue ou augmente dans les premières époques avec η = 0,01, essayez alors η = 0,001, η = 0,0001, jusqu'à ce que vous trouviez la valeur à laquelle le coût diminue dans les premières époques. Cette procédure vous donnera l'ordre de la valeur seuil η. Si vous le souhaitez, vous pouvez affiner votre évaluation en choisissant la valeur la plus élevée pour η, à laquelle le coût diminue dans les premières époques, par exemple, η = 0,5 ou η = 0,2 (l'ultra-précision n'est pas nécessaire ici). Cela nous donne une estimation de la valeur seuil η.

La valeur réelle de η ne doit évidemment pas dépasser le seuil sélectionné. En fait, pour que la valeur η reste utile pendant de nombreuses époques, il vaut mieux utiliser une valeur deux fois plus petite que le seuil. Un tel choix vous permettra généralement d'apprendre de nombreuses époques sans ralentir considérablement votre apprentissage.

Dans le cas des données MNIST, suivre cette stratégie conduira à une estimation de l'ordre seuil de η à 0,1. Après un certain raffinement, nous obtenons la valeur η = 0,5. En suivant la recette ci-dessus, nous devrions utiliser η = 0,25 pour notre vitesse d'apprentissage. Mais en fait, j'ai trouvé que η = 0,5 fonctionnait bien pendant 30 époques, donc je ne craignais pas de le diminuer.

Tout cela semble assez simple. Cependant, l'utilisation du coût de la formation pour sélectionner η semble contredire ce que j'ai dit plus tôt - que nous choisissons des hyperparamètres, évaluant l'efficacité du réseau en utilisant des données de confirmation sélectionnées. En fait, nous utiliserons la précision de la confirmation pour sélectionner les hyperparamètres de régularisation, la taille du mini-paquet et des paramètres de réseau tels que le nombre de couches et de neurones cachés, etc. Pourquoi faisons-nous les choses différemment avec la vitesse d'apprentissage? Honnêtement, ce choix est dû à mes préférences esthétiques personnelles et est probablement biaisé. L'argument est que d'autres hyperparamètres devraient améliorer la précision de classification finale sur l'ensemble de test, il est donc logique de les choisir en fonction de la précision de la confirmation. Cependant, le taux d'apprentissage n'affecte qu'indirectement la précision de la classification finale. Son objectif principal est de contrôler la taille du pas de la descente en pente et de suivre le coût de la formation de la meilleure façon afin de reconnaître une taille de pas trop grande. Mais c'est toujours une préférence esthétique personnelle. Dans les premiers stades de la formation, le coût de la formation ne diminue généralement que si la précision de la confirmation augmente, donc dans la pratique, peu importe les critères à utiliser.

Utiliser un arrêt précoce pour déterminer le nombre d'époques d'entraînement

Comme nous l'avons mentionné dans ce chapitre, un arrêt précoce signifie qu'à la fin de chaque ère, nous devons calculer la précision de la classification sur les données justificatives. Quand il cesse de s'améliorer, nous arrêtons de travailler. En conséquence, la définition du nombre d'époques devient une affaire simple. En particulier, cela signifie que nous n'avons pas besoin de comprendre spécifiquement comment le nombre d'époques dépend d'autres hyperparamètres. Cela se produit automatiquement. De plus, un arrêt précoce nous empêche également automatiquement de se recycler. Ceci, bien sûr, est bon, bien que dans les premiers stades des expériences, il puisse être utile de désactiver l'arrêt précoce afin que vous puissiez voir des signes de recyclage et les utiliser pour affiner l'approche de régularisation.

Pour mettre en œuvre l'OR, nous devons décrire plus précisément ce que signifie «arrêter l'amélioration de la précision de la classification». Comme nous l'avons vu, la précision peut aller très loin, même lorsque la tendance générale s'améliore. Si nous nous arrêtons pour la première fois, lorsque la précision diminue, nous n'atteindrons certainement pas de nouvelles améliorations possibles. La meilleure approche consiste à arrêter l'apprentissage si la meilleure précision de classification ne s'améliore pas pendant longtemps. Supposons, par exemple, que nous soyons engagés dans le MNIST. Ensuite, nous pouvons décider d'arrêter le processus si la précision de la classification ne s'est pas améliorée au cours des dix dernières époques. Cela garantit que nous ne nous arrêtons pas trop tôt en raison d'un échec de la formation, mais nous n'attendrons pas éternellement les améliorations qui ne se produiront pas.

Cette règle «aucune amélioration sur dix époques» convient bien à l'étude initiale du MNIST. Cependant, les réseaux peuvent parfois atteindre un plateau proche d'une certaine précision de classification, y rester pendant un certain temps, puis recommencer à s'améliorer. Si vous devez obtenir de très bonnes performances, la règle «pas d'amélioration sur dix époques» peut être trop agressive pour cela. Par conséquent, je recommande d'utiliser la règle «pas d'amélioration pendant dix époques» pour les expériences primaires, et d'adopter progressivement des règles plus souples lorsque vous commencez à mieux comprendre le comportement de votre réseau: «sans améliorations en vingt époques», «sans améliorations en cinquante époques», etc. plus loin. Bien sûr, cela nous donne un autre hyperparamètre pour l'optimisation! Mais en pratique, cet hyperparamètre est généralement facile à régler pour de bons résultats. Et pour les tâches autres que le MNIST, la règle «pas d'amélioration sur dix époques» peut être trop agressive, ou pas assez agressive, selon les détails d'une tâche particulière.Cependant, après avoir expérimenté un peu, il est généralement assez facile de trouver une stratégie d'arrêt précoce appropriée.

Nous n'avons pas encore utilisé d'arrêt précoce dans nos expériences avec MNIST. Cela est dû au fait que nous avons fait de nombreuses comparaisons de différentes approches de l'apprentissage. Pour de telles comparaisons, il est utile d'utiliser le même nombre d'époques dans tous les cas. Cependant, cela vaut la peine de changer network2.py en introduisant le RO dans le programme.

Les tâches

• Modifiez network2.py pour que le bon de commande y apparaisse selon la règle «pas de changement pour n époques», où n est un paramètre configurable.
• Pensez à une règle d'arrêt précoce autre que «inchangée dans n ères». Idéalement, la règle devrait rechercher un compromis entre l'obtention d'une précision avec une confirmation élevée et un temps d'entraînement assez court. Ajoutez une règle à network2.py et exécutez trois expériences comparant la précision de validation et le nombre d'époques d'apprentissage avec la règle «aucun changement sur 10 époques».

Plan de changement de vitesse d'apprentissage

Alors que nous avons gardé la vitesse d'apprentissage η constante. Cependant, il est souvent utile de le modifier. Aux premiers stades du processus de formation, les poids sont plus susceptibles d'être attribués complètement faux. Par conséquent, il sera préférable d'utiliser une vitesse d'entraînement élevée, ce qui accélérera le changement de poids. Ensuite, vous pouvez réduire la vitesse de l'entraînement pour effectuer un réglage plus fin des échelles.

Comment esquisser un plan pour changer la vitesse d'apprentissage? Ici, vous pouvez appliquer de nombreuses approches. Une option naturelle consiste à utiliser la même idée de base que dans RO. Nous maintenons la vitesse d'apprentissage constante jusqu'à ce que la précision de la confirmation commence à se détériorer. Ensuite, nous réduisons le CO d'une certaine quantité, disons, deux ou dix fois. Nous répétons cela plusieurs fois jusqu'à ce que le CO soit 1024 (ou 1000) fois inférieur à celui initial. Et terminer la formation.

Un plan pour changer la vitesse d'apprentissage peut améliorer l'efficacité et ouvre également de grandes opportunités pour choisir un plan. Et cela peut être un casse-tête - vous pouvez passer une éternité à optimiser le plan. Pour les premières expériences, je suggérerais d'utiliser une seule valeur constante de CO. Cela vous donnera une bonne première approximation. Plus tard, si vous voulez retirer la meilleure efficacité du réseau, cela vaut la peine d'expérimenter le plan pour changer la vitesse d'apprentissage comme je l'ai décrit. Un travail scientifique assez facile à lire de 2010 démontre les avantages des vitesses d'apprentissage variables lors de l'attaque du MNIST.

Exercice

• Modifiez network2.py afin qu'il implémente le plan suivant pour changer la vitesse d'apprentissage: divisez par deux le CR à chaque fois que la précision de la confirmation satisfait à la règle «pas de changement dans 10 époques», et arrêtez l'apprentissage lorsque la vitesse d'apprentissage tombe à 1/128 de la vitesse initiale.

Le paramètre de régularisation λ

Je recommande de commencer sans aucune régularisation (λ = 0,0) et de déterminer la valeur de η, comme indiqué ci-dessus. En utilisant la valeur sélectionnée de η, nous pouvons ensuite utiliser les données de support pour sélectionner une bonne valeur de λ. Commencez avec λ = 1.0 (je n'ai pas de bons arguments en faveur d'un tel choix), puis augmentez ou diminuez-le de 10 fois afin d'augmenter l'efficacité du travail avec les données de confirmation. Après avoir trouvé le bon ordre de grandeur, nous pouvons affiner la valeur de λ plus précisément. Après cela, il est nécessaire de revenir à nouveau à l'optimisation η.

Exercice

• , , λ η. , λ? , η?

Si vous utilisez les recommandations de cette section, vous verrez que les valeurs sélectionnées de η et λ ne correspondent pas toujours exactement à celles que j'ai utilisées précédemment. C'est juste que le livre a des limitations de texte, ce qui rend parfois impossible l'optimisation des hyperparamètres. Rappelez-vous toutes les comparaisons des différentes approches de formation sur lesquelles nous avons travaillé - comparer la fonction de coût quadratique et l'entropie croisée, les anciennes et les nouvelles méthodes d'initialisation des poids, en commençant par et sans régularisation, etc. Pour donner un sens à ces comparaisons, j'ai essayé de ne pas modifier les hyperparamètres entre les approches comparées (ou de les mettre à l'échelle correctement). Bien sûr, il n'y a aucune raison pour que les mêmes hyperparamètres soient optimaux pour toutes les différentes approches d'apprentissage, donc les hyperparamètres que j'utilise sont le résultat d'un compromis.

Comme alternative, je pourrais essayer d'optimiser tous les hyper paramètres pour chaque approche d'apprentissage au maximum. Ce serait une approche meilleure et plus honnête, car nous tirerions le meilleur parti de chaque approche de l'apprentissage. Cependant, nous avons fait des dizaines de comparaisons, et en pratique, cela serait trop coûteux en calcul. Par conséquent, j'ai décidé de faire un compromis, d'utiliser des options d'hyperparamètre assez bonnes (mais pas nécessairement optimales).

Taille du mini pack

Comment choisir la taille du mini-package? Pour répondre à cette question, supposons d'abord que nous sommes engagés dans une formation en ligne, c'est-à-dire que nous utilisons un mini-package de taille 1.

Le problème évident de l'apprentissage en ligne est que l'utilisation de mini-packages consistant en un seul exemple de formation entraînera de graves erreurs dans l'estimation du gradient. Mais en fait, ces erreurs ne présenteront pas un problème aussi grave. La raison en est que les estimations de gradient individuelles n'ont pas besoin d'être très précises. Nous avons juste besoin d'obtenir une estimation suffisamment précise pour que notre fonction de coût diminue. C'est comme si vous essayiez d'atteindre le pôle magnétique nord, mais vous auriez une boussole peu fiable, avec chaque mesure erronée de 10 à 20 degrés. Si vous vérifiez la boussole assez souvent et qu'elle indique en moyenne la bonne direction, vous pourrez éventuellement vous rendre au pôle magnétique nord.

Compte tenu de cet argument, il semble que nous devrions utiliser l'apprentissage en ligne. Mais en réalité, la situation est un peu plus compliquée. Dans la tâche du dernier chapitre, j'ai souligné que pour calculer la mise à jour du gradient pour tous les exemples dans le mini-package, vous pouvez utiliser des techniques de matrice en même temps, plutôt qu'une boucle. En fonction des détails de votre matériel et de la bibliothèque d'algèbre linéaire, il peut s'avérer beaucoup plus rapide de calculer une estimation pour un mini-paquet de, disons, 100 que de calculer une estimation de gradient pour un mini-paquet dans un cycle pour 100 exemples de formation. Cela peut s'avérer, par exemple, seulement 50 fois plus lent, et non 100.

Au début, il semble que cela ne nous aide pas beaucoup. Avec une taille de mini-paquet de 100, la règle de formation pour les poids ressemble à:

$$

$$w \rightarrow w' = w-\eta \frac{1}{100} \sum_x \nabla C_x \tag{100}$$

où la sommation passe en revue les exemples de formation dans le mini-package. Comparez avec

$$

$$w \rightarrow w' = w-\eta \nabla C_x \tag{101}$$

pour l'apprentissage en ligne. Même s'il faut 50 fois plus de temps pour mettre à jour le mini-package, la formation en ligne semble toujours être la meilleure option, car nous serons mis à jour plus souvent. Mais supposons, cependant, que dans le cas du mini-package, nous avons augmenté la vitesse d'apprentissage de 100 fois, puis la règle de mise à jour se transforme en:

$$

$$w \rightarrow w' = w-\eta \sum_x \nabla C_x \tag{102}$$

Cela est similaire à 100 étapes distinctes de l'apprentissage en ligne avec une vitesse d'apprentissage de η. Cependant, une étape de l'apprentissage en ligne ne prend que 50 fois plus de temps. Bien sûr, en réalité, il ne s'agit pas exactement de 100 niveaux d'apprentissage en ligne, car dans le mini-package, tous les ∇C _x sont évalués pour le même ensemble de poids, contrairement à l'apprentissage cumulatif qui se produit dans le cas en ligne. Et pourtant, il semble que l'utilisation de mini-packages plus grands accélérera le processus.

Compte tenu de tous ces facteurs, choisir la meilleure taille de mini-pack est un compromis. Choisissez trop petit et ne profitez pas pleinement des bonnes bibliothèques de matrices optimisées pour un matériel rapide. Choisissez trop grand et ne mettra pas à jour le poids assez souvent. Vous devez choisir une valeur de compromis qui maximise la vitesse d'apprentissage. Heureusement, le choix de la taille du mini-paquet à laquelle la vitesse est maximisée est relativement indépendant des autres hyperparamètres (à l'exception de l'architecture générale), donc, pour trouver une bonne taille de mini-paquet, il n'est pas nécessaire de les optimiser. Par conséquent, il suffira d'utiliser des valeurs acceptables (pas nécessairement optimales) pour d'autres hyperparamètres, puis d'essayer plusieurs tailles différentes de mini-paquets, en mettant à l'échelle η, comme indiqué ci-dessus.Construisez un graphique de la précision de la confirmation en fonction du temps (temps réel écoulé, pas des époques!), Et choisissez une taille de mini-paquet qui donne l'amélioration des performances la plus rapide. Avec la taille de mini-paquet sélectionnée, vous pouvez procéder à l'optimisation d'autres hyperparamètres.

Bien sûr, comme vous l'avez sans doute déjà compris, dans notre travail, je n'ai pas effectué une telle optimisation. Dans notre mise en œuvre de l'Assemblée nationale, une approche rapide pour la mise à jour des mini-packages n'est pas du tout utilisée. J'ai simplement utilisé le mini-paquet de taille 10 sans le commenter ni l'expliquer, dans presque tous les exemples. En général, nous pourrions accélérer l'apprentissage en réduisant la taille du mini-package. Je ne l'ai pas fait, en particulier, car mes premières expériences suggéraient que l'accélération serait plutôt modeste. Mais dans les implémentations pratiques, nous aimerions certainement mettre en œuvre l'approche la plus rapide pour mettre à jour les mini-packages, et essayer d'optimiser leur taille afin de maximiser la vitesse globale.

Techniques automatisées

J'ai décrit ces approches heuristiques comme quelque chose qui doit être modifié à la main. L'optimisation manuelle est un bon moyen de se faire une idée du fonctionnement de NS. Cependant, et d'ailleurs, il n'est pas surprenant que beaucoup de travail ait déjà été fait sur l' automatisation de ce projet. Une technique courante est une recherche de grille qui tamise systématiquement une grille dans l'espace des hyperparamètres. Un aperçu des réalisations et des limites de cette technique (ainsi que des recommandations sur des alternatives faciles à mettre en œuvre) peut être trouvé en 2012 . De nombreuses techniques sophistiquées ont été proposées. Je ne les passerai pas en revue tous, mais je veux noter le travail prometteur de 2012, utilisant l'optimisation bayésienne des hyperparamètres. Le code du travail est ouvert à tous , et avec un certain succès a été utilisé par d'autres chercheurs.

Résumer

En utilisant les règles de pratique que j'ai décrites, vous n'obtiendrez pas le meilleur résultat possible de votre PS. Mais ils sont susceptibles de vous fournir un bon point de départ et une base pour de nouvelles améliorations. En particulier, j'ai essentiellement décrit les hyperparamètres indépendamment. En pratique, il existe un lien entre eux. Vous pouvez expérimenter avec η, décider que vous avez trouvé la valeur correcte, puis commencer à optimiser λ et constater qu'elle viole votre optimisation η. Dans la pratique, il est utile de se déplacer dans différentes directions, en s'approchant progressivement des bonnes valeurs. Surtout, gardez à l'esprit que les approches heuristiques que j'ai décrites sont de simples règles de pratique, mais pas quelque chose de gravé dans la pierre. Vous devez rechercher des signes que quelque chose ne fonctionne pas et avoir le désir d'expérimenter. En particuliersurveillez attentivement le comportement de votre réseau de neurones, en particulier l'exactitude de la confirmation.

La complexité du choix des hyperparamètres est aggravée par le fait que la connaissance pratique de leur choix est répartie sur de nombreux travaux et programmes de recherche, et n'est souvent que dans la tête des praticiens individuels. Il y a énormément de travail avec des descriptions de ce qu'il faut faire (souvent en conflit les uns avec les autres). Cependant, il existe plusieurs travaux particulièrement utiles qui synthétisent et mettent en évidence une grande partie de ces connaissances. Dans le Joshua Benji de 2012 donne des conseils pratiques sur l'utilisation de descente de gradient de rétropropagation et de formation pour l'Assemblée nationale, y compris l'Assemblée nationale et profonde. Benjio décrit de nombreux détails de manière beaucoup plus détaillée. Que moi, y compris une recherche systématique d'hyperparamètres. Un autre bon travail est le travail.1998 Yanna Lekuna et autres. Les deux ouvrages figurent dans le livre extrêmement utile de 2012, qui contient de nombreuses astuces souvent utilisées à l'Assemblée nationale: " Réseaux de neurones: astuces d'artisanat ". Le livre coûte cher, mais bon nombre de ses articles ont été publiés sur Internet par leurs auteurs, et ils peuvent être trouvés dans les moteurs de recherche.

A partir de ces articles, et surtout de nos propres expériences, une chose devient claire: le problème de l'optimisation des hyperparamètres ne peut être qualifié de complètement résolu. Il y a toujours une autre astuce que vous pouvez essayer d'améliorer l'efficacité. Les écrivains ont un dicton selon lequel un livre ne peut pas être terminé, mais peut seulement être abandonné. Il en va de même pour l'optimisation NS: l'espace des hyperparamètres est si vaste que l'optimisation ne peut pas être terminée, mais ne peut être arrêtée, laissant la NS aux descendants. Votre objectif sera donc de développer un workflow qui vous permettra de réaliser rapidement une bonne optimisation, tout en vous laissant la possibilité d'essayer des options d'optimisation plus détaillées si nécessaire.

Les difficultés de sélection des hyperparamètres font que certaines personnes se plaignent que les NS nécessitent trop d'efforts par rapport aux autres techniques de MO. J'ai entendu de nombreuses variantes de plaintes comme: «Oui, une NS bien réglée peut donner la meilleure efficacité lors de la résolution d'un problème. Mais d'un autre côté, je peux essayer une forêt aléatoire [ou SVM, ou toute autre technologie préférée], et ça marche. Je n'ai pas le temps de déterminer quelle NA me convient. " Bien sûr, d’un point de vue pratique, il est bon d’avoir des techniques faciles à utiliser avec un ami. C'est particulièrement bon lorsque vous commencez tout juste à travailler sur une tâche, et il n'est toujours pas clair si le MO peut aider à la résoudre. D'un autre côté, s'il est important pour vous d'obtenir des résultats optimaux, vous devrez peut-être essayer plusieurs approches qui nécessitent des connaissances plus spécialisées. Ce serait génialsi la MO était toujours facile, mais il n'y a aucune raison pour que ce soit a priori trivial.

Autres techniques

Chacune des techniques développées dans ce chapitre est valable en soi, mais ce n'est pas la seule raison pour laquelle je les ai décrites. Il est plus important de vous familiariser avec certains des problèmes qui peuvent survenir dans le domaine de l'AN, et avec un style d'analyse qui peut aider à les surmonter. D'une certaine manière, nous apprenons à penser à la NS. Dans la suite de ce chapitre, je décrirai brièvement un ensemble d'autres techniques. Leurs descriptions ne seront pas aussi profondes que dans les précédentes, mais elles devraient transmettre certaines sensations concernant la variété des techniques rencontrées dans le domaine de la NA.

Variations de descente de gradient stochastique

La descente du gradient stochastique par rétropropagation nous a bien servi lors de l'attaque du problème de la classification des nombres manuscrits du MNIST. Cependant, il existe de nombreuses autres approches pour optimiser la fonction de coût, et elles montrent parfois une efficacité supérieure à celle de la descente de gradient stochastique avec des mini-packages. Dans cette section, je décris brièvement deux de ces approches, la Hesse et l'élan.

Hessian

Pour commencer, mettons de côté l'Assemblée nationale. Au lieu de cela, nous considérons simplement le problème abstrait de minimisation de la fonction de coût C de nombreuses variables, w = w1, w2, ..., c'est-à-dire C = C (w). Selon le théorème de Taylor, la fonction de coût au point w peut être approximée:

$$

$$C(w+\Delta w) = C(w) + \sum_j \frac{\partial C}{\partial w_j} \Delta w_j \nonumber \\ + \frac{1}{2} \sum_{jk} \Delta w_j \frac{\partial^2 C}{\partial w_j \partial w_k} \Delta w_k + \ldots \tag{103}$$

Nous pouvons le réécrire de manière plus compacte

$$

$$C(w+\Delta w) = C(w) + \nabla C \cdot \Delta w + \frac{1}{2} \Delta w^T H \Delta w + \ldots \tag{104}$$

où ∇C est le vecteur de gradient ordinaire et H est la matrice, connue sous le nom de matrice de Hesse , à la place de jk dans laquelle ∂ ² C / ∂w _j ∂w _k . Supposons que nous approchions C en abandonnant les termes d'ordre supérieur se cachant derrière les points de suspension dans la formule:

$$

$$C(w+\Delta w) \approx C(w) + \nabla C \cdot \Delta w + \frac{1}{2} \Delta w^T H \Delta w \tag{105}$$

En utilisant l'algèbre, il peut être démontré que l'expression sur le côté droit peut être minimisée en sélectionnant:

$$

$$\Delta w = -H^{-1} \nabla C \tag{106}$$

À strictement parler, pour que ce ne soit qu'un minimum, et pas seulement un extremum, nous devons supposer que la matrice de Hesse est plus définitivement positive. Intuitivement, cela signifie que la fonction C est comme une vallée, pas une montagne ou une selle.

Si (105) est une bonne approximation de la fonction de coût, il est prévu que la transition du point w au point w + Δw = w - H - 1 −C devrait réduire considérablement la fonction de coût. Cela offre un algorithme de minimisation des coûts possible:

• Sélectionnez le point de départ w.
• Mettez à jour w en un nouveau point, w ′ = w - H ⁻¹ ∇C, où les H de Hesse et ∇C sont calculés en w.
• w' , w′′=w′−H′ ⁻¹ ∇′C, H ∇C w'.
• ...

En pratique, (105) n'est qu'une approximation, et il vaut mieux faire des pas plus petits. Nous le ferons en mettant constamment à jour w par Δw = −ηH - 1∇C, où η est la vitesse d'apprentissage.

Cette approche de minimisation de la fonction de coût est connue sous le nom d'optimisation de Hesse. Il existe des résultats théoriques et empiriques montrant que les méthodes de Hesse convergent vers un minimum en moins d'étapes qu'une descente de gradient standard. En particulier, en incluant des informations sur les changements de second ordre dans la fonction de coût, il est possible d'éviter de nombreuses pathologies rencontrées en descente de gradient dans l'approche hessoise. De plus, il existe des versions de l'algorithme de rétropropagation qui peuvent être utilisées pour calculer la Hesse.

Si l'optimisation de la Hesse est si cool, alors pourquoi ne l'utilisons-nous pas dans notre NS? Malheureusement, bien qu'il possède de nombreuses propriétés souhaitables, il en existe une très indésirable: elle est très difficile à mettre en pratique. Une partie du problème est la taille énorme de la matrice de Hesse. Supposons que nous ayons un NS avec 10 ⁷ poids et décalages. Ensuite, dans la matrice de Hesse correspondante, il y aura 10 ⁷ × 10 ⁷ = 10 ¹⁴ éléments. Trop! En conséquence , il s'avère très difficile de calculer H ⁻¹ ∇C en pratique. Mais cela ne signifie pas qu'il est inutile de la connaître. De nombreuses options de descente de gradient sont inspirées de l'optimisation de la Hesse, elles évitent simplement le problème des matrices excessivement grandes. Jetons un œil à l'une de ces techniques, la descente en gradient d'impulsion.

Descente de gradient basée sur les impulsions

Intuitivement, l'avantage de l'optimisation de Hesse est qu'elle inclut non seulement des informations sur le gradient, mais également des informations sur son changement. La descente de gradient basée sur les impulsions est basée sur une intuition similaire, mais évite les grandes matrices des dérivées secondes. Pour comprendre la technique de l'impulsion, rappelons notre première image de descente en gradient, dans laquelle nous avons examiné une balle roulant dans une vallée. Ensuite, nous avons vu que la descente en pente, contrairement à son nom, ne ressemble que légèrement à une boule tombant au fond. La technique d'impulsion modifie la descente du gradient à deux endroits, ce qui la rend plus semblable à une image physique. Elle introduit d'abord le concept de «vitesse» pour les paramètres que nous essayons d'optimiser. Le gradient essaie de changer la vitesse, pas "l'emplacement" directement, de la même manière que les forces physiques modifient la vitesse,et n'affectent qu'indirectement l'emplacement. Deuxièmement, la méthode des impulsions est une sorte de terme de friction qui réduit progressivement la vitesse.

Donnons une définition mathématique plus précise. Nous introduisons les variables de vitesse v = v1, v2, ..., une pour chaque variable correspondante w _j (dans le réseau neuronal, ces variables incluent naturellement tous les poids et déplacements). Ensuite, nous changeons la règle de mise à jour de la descente de gradient w → w ′ = w - η∇C en

$$

$$v \rightarrow v' = \mu v - \eta \nabla C \tag{107}$$

$$

$$w \rightarrow w' = w+v' \tag{108}$$

Dans les équations, μ est un hyperparamètre qui contrôle la quantité de freinage ou de friction du système. Pour comprendre la signification des équations, il est tout d'abord utile de considérer le cas où μ = 1, c'est-à-dire lorsqu'il n'y a pas de frottement. Dans ce cas, l'étude des équations montre que maintenant la «force» ∇C change la vitesse v, et la vitesse contrôle le taux de changement w. Intuitivement, la vitesse peut être gagnée en y ajoutant constamment des membres de gradient. Cela signifie que si le gradient se déplace dans environ une direction pendant plusieurs étapes de l'entraînement, nous pouvons gagner une vitesse de mouvement suffisamment élevée dans cette direction. Imaginez, par exemple, ce qui se passe en descente:



À chaque descente de la pente, la vitesse augmente et nous nous déplaçons de plus en plus vite au fond de la vallée. Cela permet à la technique de vitesse de fonctionner beaucoup plus rapidement que la descente à gradient standard. Bien sûr, le problème est que, ayant atteint le fond de la vallée, nous allons la traverser. Ou, si le gradient change trop rapidement, il se peut que nous nous déplacions dans la direction opposée. C'est le point d'introduire l'hyperparamètre μ dans (107). J'ai dit plus tôt que μ contrôle la quantité de friction dans le système; plus précisément, la quantité de frottement doit être imaginée comme 1-μ. Lorsque μ = 1, comme nous l'avons vu, il n'y a pas de frottement, et la vitesse est complètement déterminée par le gradient ∇C. Et vice versa, lorsque μ = 0, il y a beaucoup de friction, aucune vitesse n'est gagnée et les équations (107) et (108) sont réduites aux équations habituelles de descente de gradient, w → w ′ = w - η∇C. En pratique,l'utilisation de la valeur de μ dans l'intervalle entre 0 et 1 peut nous donner l'avantage de pouvoir gagner en vitesse sans risque de glisser au minimum. Nous pouvons choisir une telle valeur pour μ en utilisant les données de confirmation en attente de la même manière que nous avons choisi les valeurs pour η et λ.

Jusqu'à présent, j'ai évité de nommer l'hyperparamètre μ. Le fait est que le nom standard de μ a été mal choisi: il s’appelle le coefficient de moment. Cela peut être déroutant car μ n'est pas du tout comme le concept de momentum de la physique. Elle est beaucoup plus fortement associée au frottement. Cependant, le terme «coefficient de momentum» est largement utilisé, nous continuerons donc à l'utiliser également.

Une caractéristique intéressante de la technique d'impulsion est que presque rien ne doit être fait pour modifier la mise en œuvre de la descente de gradient pour y inclure cette technique. Nous pouvons toujours utiliser la rétropropagation pour calculer les gradients, comme précédemment, et utiliser des idées comme la vérification de mini-packs sélectionnés stochastiquement. Dans ce cas, nous pouvons obtenir certains des avantages de l'optimisation de Hesse en utilisant des informations sur les changements de gradient. Cependant, tout cela se passe sans défauts et avec seulement des changements de code mineurs. En pratique, la technique de l'impulsion est largement utilisée et contribue souvent à accélérer l'apprentissage.

Exercices

• Que se passera-t-il si nous utilisons μ> 1 dans la technique d'impulsion?
• Que se passera-t-il si nous utilisons μ <0 dans la technique d'impulsion?

Défi

• Ajoutez une descente de gradient stochastique basée sur l'élan à network2.py.

Autres approches pour minimiser la fonction de coût

De nombreuses autres approches ont été développées pour minimiser la fonction de coût, et aucun accord n'a été trouvé sur la meilleure approche. En approfondissant le sujet des réseaux de neurones, il est utile de se plonger dans d'autres technologies, de comprendre comment elles fonctionnent, quelles sont leurs forces et leurs faiblesses et comment les mettre en pratique. Dans le travail que j'ai mentionné plus tôt , plusieurs de ces techniques sont introduites et comparées, y compris la descente en gradient apparié et la méthode BFGS (et étudient également la méthode BFGS étroitement liée avec restriction de mémoire, ou L-BFGS ). Une autre technologie qui a récemment montré des résultats prometteurs., il s'agit du gradient accéléré de Nesterov, améliorant la technique d'impulsion. Cependant, la descente de gradient simple fonctionne bien pour de nombreuses tâches, en particulier lorsque vous utilisez l'élan, nous allons donc nous en tenir à la descente de gradient stochastique jusqu'à la fin du livre.

Autres modèles de neurones artificiels

Jusqu'à présent, nous avons créé notre NS en utilisant des neurones sigmoïdes. En principe, NS construit sur des neurones sigmoïdes peut calculer n'importe quelle fonction. Mais en pratique, les réseaux construits sur d'autres modèles de neurones sont parfois en avance sur ceux sigmoïdes. Selon l'application, les réseaux basés sur de tels modèles alternatifs peuvent apprendre plus rapidement, mieux se généraliser aux données de vérification, ou faire les deux. Permettez-moi de mentionner quelques modèles alternatifs de neurones pour vous donner une idée de certaines options couramment utilisées.

La variation la plus simple serait peut-être un neurone tang, remplaçant la fonction sigmoïde par une tangente hyperbolique. La sortie d'un neurone tang avec l'entrée x, un vecteur de poids w et un décalage b est spécifié comme

$$

$$\tanh(w \cdot x+b) \tag{109}$$

où tanh est naturellement tangent hyperbolique . Il s'avère qu'il est très étroitement lié au neurone sigmoïde. Pour voir cela, rappelez-vous que tanh est défini comme

$$

$$\tanh(z) \equiv \frac{e^z-e^{-z}}{e^z+e^{-z}} \tag{110}$$

En utilisant une petite algèbre, il est facile de voir que

$$

$$\sigma(z) = \frac{1+\tanh(z/2)}{2} \tag{111}$$

c'est-à-dire que tanh met à l'échelle le sigmoïde. Graphiquement, vous pouvez également voir que la fonction tanh a la même forme que le sigmoïde: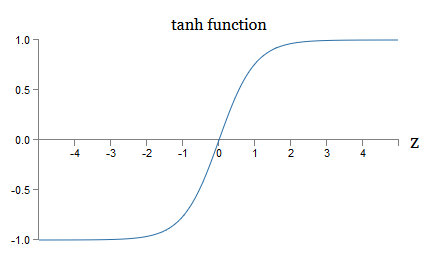



une différence entre les neurones tang et les neurones sigmoïdes est que la sortie du premier s'étend de -1 à 1, et non de 0 à 1. Cela signifie que lors de la création d'un réseau basé sur des neurones tang, vous devrez peut-être normaliser vos sorties (et, selon les détails de l'application, peut-être les entrées) un peu différemment que dans les réseaux sigmoïdes.

Comme les sigmoïdes, les neurones tang peuvent, en principe, calculer n'importe quelle fonction (bien qu'il y ait quelques astuces), marquant les entrées de -1 à 1. De plus, les idées de propagation arrière et de descente de gradient stochastique sont tout aussi faciles à appliquer à tang -neurons, ainsi que sigmoïde.

Exercice

• Démontrer l'équation (111).

Quel type de neurone doit être utilisé dans les réseaux, tang ou sigmoïde? La réponse, pour ne pas dire plus, n'est pas évidente! Cependant, il existe des arguments théoriques et certaines preuves empiriques que les neurones tang fonctionnent parfois mieux. Passons brièvement en revue l'un des arguments théoriques en faveur des neurones tang. Supposons que nous utilisons des neurones sigmoïdes et que toutes les activations sur le réseau soient positives. Considérons les poids w ^{l + 1} _jk inclus pour le neurone n ° j dans la couche n ° l + 1. Les règles de rétropropagation (BP4) nous indiquent que le gradient qui lui est associé sera égal à a ^l _k δ ^{l + 1} _j . Les activations étant positives, le signe de ce gradient sera le même que celui de δ ^{l + 1} _j. Cela signifie que si δ ^{l + 1} _{j est} positif, alors tous les poids w ^{l + 1} _jk diminueront pendant la descente du gradient, et si δ ^{l + 1} _{j est} négatif, alors tous les poids w ^{l + 1} _jkaugmentera pendant la descente du gradient. En d'autres termes, tous les poids associés au même neurone augmenteront ou diminueront ensemble. Et c'est un problème, car vous devrez peut-être augmenter certains poids tout en en réduisant d'autres. Mais cela ne peut se produire que si certaines activations d'entrée ont des signes différents. Cela suggère la nécessité de remplacer le sigmoïde par une autre fonction d'activation, par exemple la tangente hyperbolique, qui permet aux activations d'être à la fois positives et négatives. En effet, puisque tanh est symétrique par rapport à zéro, tanh (−z) = −tanh (z), on peut s'attendre à ce qu'en gros, les activations dans les couches cachées soient également réparties entre positif et négatif. Cela contribuera à garantir qu'il n'y a pas de biais systématique dans les mises à jour des échelles dans un sens ou dans l'autre.

Dans quelle mesure cet argument doit-il être pris au sérieux? Après tout, il est heuristique, ne fournit pas de preuve stricte que les neurones tang sont supérieurs aux neurones sigmoïdes. Peut-être que les neurones sigmoïdes ont des propriétés qui compensent ce problème? En effet, dans de nombreux cas, la fonction tanh a montré des avantages minimes à nuls par rapport à la sigmoïde. Malheureusement, nous n'avons pas de méthodes simples et rapidement mises en œuvre pour vérifier quel type de neurone apprendra plus rapidement ou se révélera plus efficace pour généraliser pour un cas particulier.

Une autre variante d'un neurone sigmoïde est un neurone linéaire rectifié, ou unité linéaire rectifiée, ReLU. La sortie ReLU avec l'entrée x, le vecteur des poids w et le décalage b est spécifié comme suit:

$$

$$\max(0, w \cdot x+b) \tag{112}$$

La fonction de redressement graphique max (0, z) ressemble à ceci:



De tels neurones, évidemment, sont très différents des neurones sigmoïdes et tang. Cependant, ils sont similaires en ce sens qu'ils peuvent également être utilisés pour calculer n'importe quelle fonction, et ils peuvent être entraînés à l'aide de la propagation arrière et de la descente de gradient stochastique.

Quand devrais-je utiliser ReLU au lieu des neurones sigmoïdes ou tang? Dans des travaux récents sur la reconnaissance d'image ( 1 , 2 , 3 , 4) Les avantages sérieux de l'utilisation de ReLU ont été trouvés sur presque tout le réseau. Cependant, comme avec les neurones tang, nous n'avons pas encore une compréhension vraiment approfondie de quand exactement quelles ReLU seront préférables, et pourquoi. Pour avoir une idée de certains problèmes, rappelez-vous que les neurones sigmoïdes cessent d'apprendre lorsqu'ils sont saturés, c'est-à-dire lorsque la sortie est proche de 0 ou 1. Comme nous l'avons vu à plusieurs reprises dans ce chapitre, le problème est que les membres σ 'réduisent le gradient qui ralentit l'apprentissage. Les neurones Tang souffrent de difficultés similaires de saturation. Dans le même temps, une augmentation de l'entrée pondérée sur ReLU ne la rendra jamais saturée, par conséquent, aucun ralentissement correspondant de la formation ne se produira. D'un autre côté, lorsque l'entrée pondérée sur le ReLU est négative, le gradient disparaît et le neurone cesse d'apprendre du tout.Ce ne sont là que quelques-uns des nombreux problèmes qui rendent difficile de comprendre quand et comment les ReLU se comportent mieux que les neurones sigmoïdes ou tang.

J'ai brossé un tableau de l'incertitude, en soulignant que nous n'avons pas encore une solide théorie du choix des fonctions d'activation. En effet, ce problème est encore plus compliqué que je l'ai décrit, car il existe une infinité de fonctions d'activation possibles. Lequel nous donnera le réseau le plus rapide à apprendre? Lequel donnera la plus grande précision dans les tests? Je suis surpris du peu d'études vraiment approfondies et systématiques sur ces questions. Idéalement, nous devrions avoir une théorie qui nous explique en détail comment choisir (et éventuellement changer à la volée) nos fonctions d'activation. D'un autre côté, il ne faut pas se laisser arrêter par l'absence d'une théorie complète! Nous avons déjà des outils puissants, et avec leur aide, nous pouvons réaliser des progrès significatifs. Jusqu'à la fin du livre, j'utiliserai les neurones sigmoïdes comme principaux,car ils fonctionnent bien et donnent des illustrations concrètes des idées clés liées à l'Assemblée nationale. Mais gardez à l'esprit que les mêmes idées peuvent être appliquées à d'autres neurones, et ces options ont leurs avantages.

: , , ? ?

: , . , . . : , , ?

—

Lors d’une conférence sur les bases de la mécanique quantique, j’ai remarqué quelque chose qui semblait une drôle d’habitude de discours: à la fin du rapport, les questions du public commençaient souvent par la phrase: «J'aime vraiment votre point de vue, mais ...» Les fondamentaux quantiques ne sont pas tout à fait mon domaine habituel, et j'ai attiré l'attention sur ce style de poser des questions parce que lors d'autres conférences scientifiques, je ne me suis pratiquement pas réuni pour que le questionneur montre de la sympathie pour le point de vue de l'orateur. À ce moment-là, j'ai décidé que la prévalence de telles questions indiquait que les progrès dans les fondamentaux quantiques avaient été réalisés un peu, et que les gens commençaient tout juste à prendre de l'élan. Plus tard, j'ai réalisé que cette évaluation était trop sévère. Les orateurs ont lutté avec certains des problèmes les plus difficiles que les esprits humains aient jamais rencontrés. Naturellement, les progrès ont été lents!Cependant, il était toujours utile d'entendre des nouvelles de la pensée des gens sur ce domaine, même s'ils n'avaient rien ou presque.

Dans ce livre, vous avez peut-être remarqué une «tique nerveuse» semblable à la phrase «Je suis très impressionné». Pour expliquer ce que nous avons, j'ai souvent eu recours à des mots comme «heuristiquement» ou «à peu près», suivis d'une explication d'un phénomène particulier. Ces histoires sont crédibles, mais les preuves empiriques étaient souvent assez superficielles. Si vous étudiez la littérature de recherche, vous verrez que des histoires de ce genre apparaissent dans de nombreux articles de recherche sur les réseaux de neurones, souvent en compagnie d'une petite quantité de preuves à l'appui. Comment nous relions-nous à ces histoires?

Dans de nombreux domaines scientifiques - en particulier lorsque des phénomènes simples sont considérés - on peut trouver des preuves très strictes et fiables d'hypothèses très générales. Mais à l'Assemblée nationale, il existe un grand nombre de paramètres et d'hyperparamètres, et il existe des relations extrêmement complexes entre eux. Dans de tels systèmes incroyablement complexes, il est extrêmement difficile de faire des déclarations générales fiables. La compréhension de la NS dans toute sa plénitude, comme les fondements quantiques, teste les limites de l'esprit humain. Souvent, nous devons nous passer de preuves en faveur ou contre plusieurs cas particuliers spécifiques d'une déclaration générale. En conséquence, ces déclarations doivent parfois être modifiées ou abandonnées, à mesure que de nouvelles preuves émergent.

L'une des approches de cette situation consiste à considérer que toute histoire heuristique sur la NS implique un certain défi. Par exemple, considérez l'explication que j'ai citée pour expliquer pourquoi une exception (abandon) du travail en 2012 fonctionne.: «Cette technique réduit l'adaptation articulaire complexe des neurones, car un neurone ne peut pas compter sur la présence de certains voisins. En fin de compte, il doit apprendre des traits plus fiables qui peuvent être utiles pour travailler avec de nombreux sous-ensembles aléatoires différents de neurones. » Une déclaration riche et provocante, sur la base de laquelle vous pouvez construire tout un programme de recherche, dans lequel vous devrez découvrir ce qui est vrai, où c'est faux, et ce qui doit être clarifié et changé. Et maintenant, il y a vraiment toute une industrie de chercheurs qui étudient l'exception (et ses nombreuses variantes), essayant de comprendre comment cela fonctionne et quelles sont ses limites. C'est donc avec de nombreuses autres approches heuristiques que nous avons discuté. Chacun d'eux n'est pas seulement une explication potentielle,mais aussi un défi pour la recherche et une compréhension plus approfondie.

Bien sûr, pas une seule personne n'aura assez de temps pour enquêter suffisamment en profondeur sur toutes ces explications heuristiques. Il faudra des décennies à l'ensemble de la communauté des chercheurs de la Nouvelle-Écosse pour élaborer une théorie de la formation de la Nouvelle-Écosse vraiment puissante fondée sur des preuves. Est-ce à dire qu'il vaut la peine de rejeter les explications heuristiques comme laxistes et manquant de preuves? Non!Nous avons besoin d'une heuristique qui inspirera notre réflexion. Cela ressemble à l'ère des grandes découvertes géographiques: les premiers érudits ont souvent agi (et fait des découvertes) sur la base de croyances qui se sont trompées de manière sérieuse. Plus tard, nous avons corrigé ces erreurs, reconstituant nos connaissances géographiques. Lorsque vous comprenez mal quelque chose - comme les chercheurs ont compris la géographie et comme nous comprenons la NS aujourd'hui - il est plus important d'étudier hardiment l'inconnu que d'avoir scrupuleusement raison à chaque étape de votre raisonnement. Par conséquent, vous devriez considérer ces histoires comme des instructions utiles sur la façon de réfléchir sur les SN, en maintenant une bonne conscience de leurs limites et en surveillant attentivement la fiabilité des preuves dans chaque cas. En d'autres termes, nous avons besoin de bonnes histoires pour la motivation et l'inspiration, et des enquêtes approfondies scrupuleuses - afin depour découvrir des faits réels.