🏐 👵 ☝️ Physique et économie. Différence gnoséologique et sa manifestation en informatique 👩‍❤️‍👩 💃🏻 🆎

Je suis venu dans le monde de l'informatique de la physique théorique. Il était principalement engagé dans des tâches économiques. Engagé - ceci: analyse, savoirs traditionnels, déclaration, conception, programmation. Naturellement, j'ai constamment comparé les approches physiques et économiques pour comprendre les lois de la nature et de l'économie, respectivement. Un certain point de vue a mûri sur ce sujet. À son sujet et sera discuté.

1. À propos de la cognition en général

Il existe deux approches de la cognition:

L'approche d'Aristote . Il s'agit d'une approche holistique et traite l'objet comme une boîte noire. Le phénomène, l'objet est étudié dans toute la réalité dans son ensemble. Et la réalité dit, par exemple, que les corps lourds tombent au sol plus rapidement que les corps légers; qui a laissé à lui-même un corps en mouvement s'arrête progressivement. L'approche d'Aristote traite le phénomène comme une réalité intégrale, il peut donc être qualifié de phénoménologique.

L'approche de Galileo . Il s'agit d'une approche systémique analytique. C'est l'approche diviser pour mieux régner. Le phénomène, l'objet sont décomposés en ses parties constitutives et chacune d'elles est étudiée séparément, abstraite du reste (analyse). Ensuite, les images résultantes peuvent être combinées en une seule, en tenant compte de l'interaction des composants (synthèse). Par exemple, la chute de corps est considérée comme la chute de corps dans le vide. Et là, ils se révèlent tomber avec la même accélération. Mais en réalité, les frottements contre l'air les empêchent de tomber également. Après avoir étudié cette force séparément, nous pouvons expliquer le résultat d'Aristote. De même, si nous nous désengageons des forces de frottement, le corps en mouvement se déplacera sans s'arrêter. Et si l'on prend en compte la force de frottement, on obtient le résultat d'Aristote. L'approche de Galileo conduit immédiatement à la nécessité d'étudier les forces. En fin de compte, cela se traduit par un système cohérent de physique classique.

Encore une fois, pour plus de clarté.

L'approche d'Aristote . Il y a un phénomène à l'étude, "La chute du corps dans l'air au sol" - le phénomène F. Nous prenons différents corps et constatons que les corps plus lourds tombent au sol plus rapidement que les corps légers.

L'approche de Galileo . Lors de l'étude du phénomène de F, il faut tenir compte non seulement du poids. Nous étudions la chute dans l'air. Et changeons non seulement le poids, mais aussi l'air. Essayons de réduire sa densité, pour qu'au final, il n'y ait pas d'air. Ensuite, nous constatons que tous les corps tombent dans le vide avec la même accélération. Nous trouvons les paramètres d'influence sur le phénomène et essayons de créer des conditions dans lesquelles un seul paramètre est significatif. Ce n'est pas dans la nature. Par conséquent, un physicien a besoin d'un laboratoire où il pourrait faire varier les paramètres. Après avoir étudié l'influence d'un paramètre, nous pouvons procéder à l'étude de l'influence d'un autre paramètre. Nous essayons de réduire la complexité de l'approche globale à la composition d'approches plus simples. En variant la forme du corps qui tombe, on peut étudier la dépendance de la force de frottement à l'air selon la forme du corps. En faisant varier le taux de chute, nous pouvons détecter la dépendance de la force de friction sur la vitesse. En variant la hauteur de la chute, on peut détecter la dépendance de l'accélération sur la hauteur. En variant la situation géographique sur terre, nous trouvons la dépendance de l'accélération de la chute sur la géographie.

En gros, dans l'approche d'Aristote, ils étudient la réalité, et dans l'approche de Galilée, ils étudient les abstractions, et à partir d'eux, par la synthèse, ils vont à la réalité.

2. Le modèle des connaissances physiques

La physique est une théorie idéale pour de nombreuses sciences, y compris l'économie. Dans les expériences physiques, des séries discrètes de valeurs sont obtenues. Mais ils sont considérés comme une approximation des fonctions continues, qui sont en réalité des indicateurs physiques. Et les physiciens essaient de deviner ces fonctions. Galilée devina donc la parabole pour la trajectoire d'une pierre lancée en biais par rapport à l'horizon; Kepler a deviné les trajectoires des planètes - ellipses, etc. Après avoir deviné la trajectoire, nous obtenons un appareil prédictif - la capacité de calculer la valeur de coordonnées inexplorées de la trajectoire. Pour tester, ils ont mis une expérience - créer les conditions permettant à l'expérimentation d'obtenir la valeur d'intérêt. Ensuite, après avoir vérifié la valeur prédite et la valeur expérimentale, nous obtenons une confirmation ou une réfutation de la théorie. Ici parfois, l'erreur de l'erreur expérimentale joue un rôle important. La connaissance physique se résume à l'identification du déterminisme - la loi d'obtention d'un état à partir d'un état initial:

$S (t) = D (Q, S (0))$

S(0) -   D –  – ,  S(t)  S(0) Q –       . ,  ,      .

Donc, pour une pierre lancée à partir d'un point (0,0) avec une vitesse $v_0$ à un angle $α$ à l'horizon que nous avons

$$ afficher $$ x (t) = v_0 t cos⁡ (α), y (t) = v_0 t sin⁡ (α) - (gt ^ 2) / 2 $$ afficher $$

L'état initial S (0) est défini par trois paramètres: point de départ (0,0), vitesse initiale $v_0$ angle $α$ .
L'impact de l'environnement Q est donné par l'accélération de la gravité g. Lors de l'élargissement de la portée du problème (vitesse initiale élevée), g n'est plus constant.
Le déterminisme D est donné par la formule ci-dessus.

Pour une tâche plus réaliste, la friction contre l'air doit être prise en compte. Cela complique le calcul du problème, mais le principe reste le même. Au lieu de pierre, vous pouvez envisager un avion. La force de poussée de l'avion entre alors en jeu, et sa régulation par le pilote. Un facteur non physique apparaît également - la volonté du pilote. Nous ne pouvons pas en tenir compte. Mais nous savons qu'elle n'est pas illimitée: la traction ne peut pas être infinie, l'accélération ne peut pas être infinie. Cela introduit un élément de certitude dans le mouvement. Ils l'utilisent, par exemple, pour construire la trajectoire d'un missile de défense aérienne.

Revenons à la pierre volante. Il se caractérise par un nombre infini de paramètres physiques. Par exemple, seule sa forme peut être arbitrairement complexe. Mais nous sommes sûrs que dans certains domaines utiles, nous pouvons considérer la pierre comme un point matériel. Il s'agit de la principale abstraction de la mécanique classique. Tous les systèmes sont représentés comme des ensembles de points matériels en interaction. Cela fait la principale réduction cognitive - réduire le comportement d'un système complexe au comportement de ses composants élémentaires.

En relation avec la réduction cognitive mentionnée, deux approches épistémologiques peuvent être distinguées - le réductionnisme et l'holisme.

3. Réductionnisme et holisme

Le réductionnisme est le principe de la réduction des caractéristiques d'un système des caractéristiques des sous-systèmes et des caractéristiques de l'interaction des sous-systèmes. Fonctionne avec succès en physique.
Prenons par exemple le gaz. Sans le décomposer en sous-systèmes, nous pouvons opérer avec des concepts phénoménologiques expérimentaux: pression P, température T, volume V. Empiriquement, nous trouvons la relation reliant ces paramètres - l'équation d'état du gaz:

$PV = constT$

C'est ce que l'on appelle le niveau phénoménologique - travailler avec des phénomènes (phénomènes) sans entrer dans leur structure. Telle est l'approche d'Aristote.

Appliquez maintenant l'approche de Galileo. Nous décomposons le système «gaz»: imaginez-le comme un ensemble de molécules en collision. Ensuite, nous définissons P et T à travers les paramètres mécaniques de la molécule. Cela se fait en physique moléculaire. Ainsi, nous réduisons le système de gaz à des sous-systèmes de molécules. Cela clarifiera l'équation d'état ou la déduira pour les nouveaux systèmes.

En conséquence, dans les affaires, nous avons une analogie: la macroéconomie se décompose en entreprises et en ménages. Mais ici, la réduction n'est pas encore parfaite. Hélas, il n'y a pas de Newton économique. Le problème est la complexité et la disponibilité d'un facteur subjectif qui n'est pas en physique (bien qu'il y ait un débat sur le rôle du sujet en mécanique quantique).

Et maintenant sur l'holisme.

L'holisme est le principe selon lequel il peut y avoir des propriétés non réductibles dans un système. Ainsi, en biologie, la doctrine du vitalisme est basée sur le concept d'entéléchie, la force vitale inhérente au corps dans son ensemble et irréductible.

Jusqu'à présent, la physique renonce au concept de l'holisme.

4. Formule et modèles algorithmiques

Un modèle de formule est un modèle défini par une formule. Le concept de «formule» sera considéré comme connu.

Exemples en physique: équations de Newton, équations de Lagrange, équations de Maxwell, équations de Navier-Stokes, équations de Heisenberg-Schrödinger, équations d'Einstein.

Exemples tirés de l'économie: formule de Black-Scholes pour le prix de l'option, formule de masse monétaire, modèle de programmation linéaire pour l'optimisation du portefeuille financier, formules de calcul des intérêts, formules de calcul des risques.

Avec un modèle de formule, une personne peut travailler sans ordinateur. Telles sont presque toutes les mathématiques pures. Mais ici, l'algorithmique joue un rôle de plus en plus important. La solution au problème des quatre couleurs n'était donc pas réduite à une formule, mais nécessitait une solution de force brute pour de nombreux cas particuliers. Ce buste a été fait par des ordinateurs.

Modèle algorithmique - un modèle défini par un algorithme, éventuellement non réductible à une formule. Bien sûr, il est possible de classer l'algorithme en formules, mais ce ne sont pas les mêmes formules classiques. Le modèle algorithmique n'est initialement réaliste qu'à l'aide d'un ordinateur
Un modèle formel peut toujours être réduit à un modèle algorithmique.

Un exemple du premier modèle algorithmique est le problème de Fermi-Pasta-Ulam. Voici une citation du livre d'Ulam, The Adventures of Mathematics.

Devis

_{Dès l'achèvement des machines, Fermi, avec son intuition et son grand bon sens, a immédiatement compris toute leur importance dans l'étude des problèmes de physique théorique, d'astrophysique et de physique classique.} _{Nous avons discuté de ce problème de la manière la plus détaillée et avons décidé d'essayer de formuler un problème qui serait simple dans sa formulation, mais qui aurait une solution nécessitant de très longs calculs, impossible à l'aide d'un stylo et du papier ou de dispositifs informatiques mécaniques existants.} _{Après avoir discuté d'un certain nombre de problèmes possibles, nous nous sommes installés sur un problème typique lié au comportement à long terme d'un système dynamique et nécessitant une prédiction à long terme.} _{Il a considéré une chaîne élastique à deux extrémités fixes, qui est affectée non seulement par la force de déformation élastique habituelle proportionnelle à la déformation, mais également par une petite force physique non linéaire.} _{Il était nécessaire de savoir comment, après un très grand nombre de périodes d'oscillations, cette non-linéarité affectera progressivement le comportement périodique connu des oscillations dans une touche, comment les autres touches acquerront leurs amplitudes et comment, nous l'avons raisonné, le mouvement sera thermisé, imitant, peut-être, le comportement les liquides qui, étant initialement laminaires, deviennent de plus en plus turbulents, jusqu'à ce que, finalement, leur mouvement macroscopique se transforme en chaleur.}

John Pasta, un physicien récemment arrivé à Los Alamos, nous a aidés à créer des organigrammes, à programmer et à traiter des tâches chez MANIAC. Fermi a décidé d'apprendre à programmer une machine. À cette époque, c'était plus difficile à faire que maintenant, alors qu'il existait déjà des programmes prêts à l'emploi et des règles établies, et que cette procédure elle-même était automatisée. Ensuite, il a fallu apprendre différentes astuces. Fermi les a maîtrisés très rapidement et m'a appris quelque chose, bien que j'en sache déjà assez pour pouvoir évaluer quel type de tâches peuvent être résolues de cette manière, déterminer leur durée en nombre d'étapes de calcul et comprendre les principes de leur mise en œuvre.

En fin de compte, nous avons très bien sélectionné la tâche. Les résultats obtenus en termes qualitatifs étaient complètement différents même de ceux que Fermi attendait avec sa connaissance approfondie des mouvements des vagues. L'objectif initial était de voir à quelle vitesse l'énergie de la corde, à l'origine intégrée dans une simple onde sinusoïdale (une note était prise comme un ton), créerait progressivement des harmoniques plus élevées, et comment le système atteindrait un état chaotique final, décrivant comment la forme de la corde , donc la nature de la répartition de l'énergie entre des touches de plus en plus élevées. Mais rien de tel ne s'est produit. À notre grande surprise, la corde n'a commencé à jouer que sur quelques notes sourdes et, ce qui est probablement encore plus étonnant, après plusieurs centaines de vibrations alternatives réciproques, elle a de nouveau pris presque la même forme sinusoïdale qu'au début.

Je sais que Fermi considérait cela comme une «découverte mineure», comme il l'a lui-même dit. Mais il allait parler de lui un an plus tard, quand il a été invité à donner une conférence de Gibbs (un événement très honorable lors de la réunion annuelle de l'American Mathematical Society). Il est tombé malade avant la réunion et cette conférence n'a jamais eu lieu. Cependant, un rapport sur ce travail, écrit par Fermi, Pasta et moi, a néanmoins été publié - en tant que rapport sur le travail à Los Alamos.

Je dois expliquer que le mouvement d'un milieu continu, comme une chaîne par exemple, peut être étudié à l'aide d'un ordinateur si nous imaginons qu'une chaîne est constituée d'un nombre fini de particules - dans notre cas, soixante-quatre ou cent vingt-huit. (Le nombre d'éléments est mieux représenté par une puissance de deux, car cela facilite le traitement sur un ordinateur.) Ces particules sont interconnectées par des forces qui, en plus des termes de distance linéaire, contiennent également de petits termes quadratiques non linéaires. Ensuite, la machine calcule rapidement le mouvement de chacun de ces points en de courts pas de temps. Après avoir calculé une position, elle passe à une autre étape de temps et calcule une nouvelle position, et elle se répète donc plusieurs fois. Il n'y a absolument aucun moyen de faire ce calcul manuellement, cela prendrait littéralement des milliers d'années. La solution sous une forme analytique utilisant des méthodes mathématiques d'analyse classique des XIXe et XXe siècles est totalement inacceptable ici.

Les résultats étaient vraiment stupéfiants. De nombreuses tentatives ont été faites pour élucider les causes d'un tel comportement périodique et régulier, qui est devenu une source pour la littérature volumineuse sur les oscillations non linéaires existant aujourd'hui. Les travaux ont été rédigés par Martin Kruskal, un physicien de Princeton, et Norman Zabuski, un mathématicien qui travaillait au Bell Telephone Laboratory. Plus tard, Peter Lake a apporté sa brillante contribution à cette théorie. Tous ont mené une analyse intéressante des problèmes de ce type. Le mathématicien sait que le soi-disant système dynamique de Poincaré, qui comprend tant de particules, est de longueur gigantesque - en fait, à l'échelle astronomique - et qu'il revient si rapidement à sa position d'origine est le plus surprenant.

Un autre physicien de Los Alamos, James So, a décidé de voir si la période suivant ce retour très proche de la position initiale recommence à partir du même état, et que se passera-t-il après cette deuxième «période». Avec Pasta et Metropolis, il a répété toute la procédure et, étonnamment, le retour s'est produit à nouveau, mais avec une précision inférieure à environ un pour cent. Cette image a été répétée plus loin, mais après six ou douze de ces périodes, la précision a recommencé à augmenter, ce qui a indiqué l'apparition d'une certaine «super période». Ainsi, une étrangeté a été suivie d'une autre, pas moins.

Et voici un article sur Habré, racontant l'état actuel du problème Fermi-Pasta-Ulam:
Les mathématiciens ont résolu le problème de Fermi-Pasta-Ulam

5. Coordination

Par coordination du système, j'entends la définition de paramètres de base qui, en principe, déterminent l'évolution du système. Par exemple, dans la mécanique d'un point matériel, la coordination est définie par:

Force externe F
- Masse m point matériel
- Coordonnées spatiales (x, y, z) = r du point matériel
- Temps t

L'évolution du système est donnée par l'équation de Newton

$(d ^ 2 r (t)) / (dt ^ 2) = (F (t)) / m$

Quelle est la coordination de l'entité économique? J'ai déjà travaillé sur un système de Business Intelligence. Son terme principal est indicateur. La base du système est un tableau de bord. Des centaines d'indicateurs. Mais j'ai cherché en vain sur Internet une description de la base des indicateurs - un ensemble d'indicateurs qui ne peuvent être réduits à d'autres et qui, en principe, déterminent complètement l'évolution d'une entité économique. C'est-à-dire, si je comprends bien, aucune coordination n'a été faite dans l'économie. Et, par conséquent, parler d'une loi dynamique de base n'est pas encore possible. Il est seulement possible, sur la base de la connexion des indicateurs, de mener une analyse de scénario - pour répondre à la question «Qu'adviendra-t-il des indicateurs dérivés si les indicateurs sous-jacents changent en fonction du scénario donné?»

6. Exemple abstrait. Les prévisions chronologiques comme la physique

Vous pouvez poser le problème de prévision sur la base de la série temporelle réelle: ayant un certain nombre de valeurs réelles, vous devez obtenir la valeur prédite de l'indicateur - la valeur future. Cela implique une sorte de déterminisme caché des séries chronologiques. Il y a eu de nombreuses spéculations scientifiques et pseudoscientifiques à ce sujet. J'ai moi-même eu affaire à des docteurs en sciences qui ont affirmé que leur méthodologie leur permettrait d'obtenir une prévision du taux de change et ont montré les thèses correspondantes avec toutes sortes d'intervalles de confiance et d'autres attributs des lois de distribution. Mais face à la réalité, les techniques sont époustouflées.

Parfois, pour obtenir une prévision, procédez comme suit:

Prenez la série en temps réel {V (ti)}. Calendrier - étape ligne brisée.
Prenez une fonction continue W (t) telle que W (ti) = V (ti). Le graphique est une courbe continue.
Un polynôme P (t) est sélectionné qui se rapproche de W (t) avec un degré de précision suffisant. Un polynôme peut être considéré pour tous les t.
Ensuite, nous avons une prévision pour le temps futur T: V (T) = P (T)
Tout cela donne l'impression de la science, mais seulement à première vue. Oui, l'existence d'un polynôme approximatif pour W (t) est garantie par le théorème de Weierstrass issu de la matanalyse. On peut polynomiser arbitrairement précisément W (t). Mais il ne peut pas être utilisé pour des prédictions.

La valeur approximative de la série réelle est de 100% et la valeur prédictive est nulle. Les polynômes peuvent être inventés arbitrairement, mais ils donneront tous des prévisions différentes.

Lorsque le jour T arrive et que nous découvrons le vrai V (T), alors pour la série {{V (ti)}, V (T)} nous pouvons construire un nouveau polynôme Q (t) qui se rapproche arbitrairement précisément de cette série, mais le temps T n'est plus l'avenir et Q (T) n'est plus une prévision, mais une réalité. Les polynômes P (t) et Q (t) ne doivent absolument pas coïncider et pour le nouveau temps de prévision T '> T, ils afficheront des résultats différents. Autrement dit, il n'y a aucune prévision. Il semble y avoir de la science, mais aucune prévision. C'est comme une théorie médiévale des anges. Elle peut tout expliquer, mais elle ne peut rien prédire.

La différence entre l'interpolation physique et l'extrapolation de l'économie:

La précision des données empiriques : approximative en physique, précise en économie
Fonctions de domaine : continue en physique, discontinue, pas à pas en économie
Données empiriques : en physique, discrète, en économie continue avec discontinuités discrètes
Lois fondamentales : en physique là-bas. F = ma, par exemple; dans l'économie encore

7. Économie et physique

En économie, les trajectoires réelles - essentiellement discontinues - sont des fonctions constantes par morceaux. Par exemple, l'indicateur «Taux de change» peut faire un bond à tout moment. Fonctions économiques continues - approximations pour une bonne analyse (si vous avez un marteau entre les mains, alors vous voulez considérer n'importe quel objet comme un clou ...). Chaque opération comptable provoque des sauts dans les valeurs des indicateurs des dérivés des comptes. Et ce sont la majorité des indicateurs. De plus, chaque changement dans le nombre de travailleurs est discret, etc. La continuité des trajectoires économiques contraste avec la continuité de la plupart des trajectoires physiques. Par conséquent, l'appareil de la matanalyse n'est pas directement applicable aux trajectoires économiques.

Image pour la cognition physique. La trajectoire d'une pierre lancée en biais par rapport à l'horizon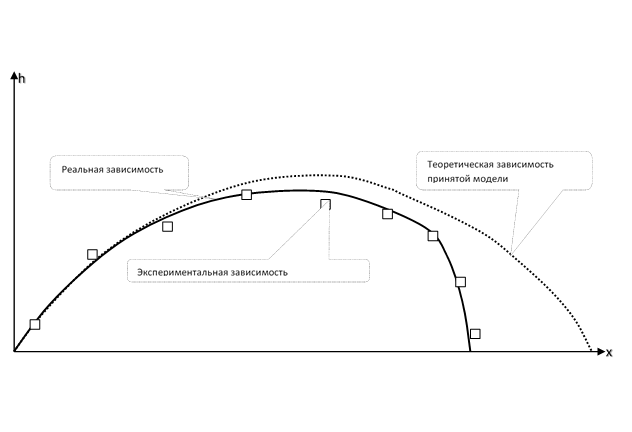

Image pour la connaissance économique. Taux de change à la banque centrale.

Il s'agit d'une véritable fonction expérimentale exacte. Il est discontinu à des moments où le taux de change change.

En physique:

Les valeurs physiques expérimentales sont presque toujours approximatives
Les valeurs physiques expérimentales forment une série discrète.
Une série discrète expérimentale est considérée comme un polygone pour une approximation continue car la réalité est continue. La notion de continuité peut s'avérer être un mensonge à de petites échelles spatiales et temporelles. La physique changera alors de visage.
Indicateurs de base bien définis
Les trajectoires théoriques et réelles sont presque toujours continues et presque toujours différenciables (la trajectoire d'un point matériel est toujours deux fois différenciable dans le temps)
Du fait de la continuité de la dynamique réelle et de la trajectoire réelle, sa bonne approximation continue a un pouvoir prédictif: dans un voisinage suffisamment petit, la fonction n'ira pas loin de sa dernière valeur réelle.

Dans l'économie:

Les valeurs économiques expérimentales peuvent être considérées comme exactes. Ce n'est qu'en macroéconomie qu'il y a un problème de précision en raison du grand nombre d'entités commerciales.
Les valeurs économiques expérimentales consistent en des intervalles de constance, interrompus à certains moments dans le temps lorsque la valeur change brusquement
Les données expérimentales ne peuvent pas être considérées comme un terrain d'essai pour une approximation continue car la réalité est discontinue.
Indicateurs de référence non entièrement définis. On ne sait pas pourquoi danser.
En raison de la discontinuité de la trajectoire réelle, toute approximation continue arbitrairement bonne ne garantit pas les prédictions dans un voisinage arbitrairement petit.
Les trajectoires réelles sont presque toujours discontinues. Cela signifie que la détermination économique nécessite une approche différente de la mécanique classique.
Dans l'économie, il existe initialement un facteur de libre arbitre d'une entité économique. Son aire de répartition est réglementée par l'État. Les limites extrêmes de cette liberté:
- Liberté totale sur un marché non réglementé par l'État
- Liberté partielle dans un marché partiellement réglementé par l'État
- Absence totale de liberté dans un État totalement centralisé où il n'y a pas de marché libre

La connaissance économique n'a pas atteint un niveau similaire à la mécanique classique:

Les composants élémentaires du type de point matériel ne sont pas définis
Non défini Q (paramètres environnementaux), on ne sait pas ce qui est important, ce qui ne l'est pas,
,
; .

. – . – . ? , . . . . , – .

, . , , - .

8. IT

8.1.

. . . . , . . . . . . . , , . . … , . . , . . . , . . . . . . . . . . . – " . - "!? , . -1840( , ). . . , . , . , . , . . , , . (). . , , , : ", . ". ! . , , - .

8.2. -

. — . , , .. . . , . . – . , . , . – . . …

. . , . , , , . , . . . . . , - . . . . , : , . . . , , . . ? . . , .

. - , .

, , . , . . , .

. . . , . , . , : , . , . . .

, – Jump Processing. , . Mais c'est une histoire complètement différente.

, . “ ”. , – . , , . – , . . , – .

8.3.

( ). . “”. . , . , . . – . . , . . . . , . . – . . , . … . ? , . , - . . . , . , , . . .

. , . , . , – . , . , – ( – ?).

8.4.

_{“ ”}

. () . . . , , . . , . . , , . . . – . , , . , . . , . Sympa. . – . , . – . . , (, ). , . . , . . , , , . . . – . . . . . . . . . : , , , , , , , , … . 100 . ( , , ) . , ( , (SQL-) ). , . C'est-à-dire . . . , . . , : ”, . . . ”.

. , . , . : . , , .

. . . , , . . . . -.

() . , , ( ), . , . , – . , , , , , . . . , , . , “” “”. , “” “”. ? , .

: . . . , . . . . — . . : . : , …

. . , . . .

Résumé

, . . - . . — . Pourquoi ça? .

: IT. .

Physique et économie. Différence gnoséologique et sa manifestation en informatique