Nous procédons au calcul des fonctions logiques selon le graphique pour une classe plus large de comportements. Nous considérons les comportements cycliques autonomes qui ne contiennent pas de signaux multiples (ou d'une autre manière: ne contiennent pas d'événements indexés). Autre limitation: pour plus de commodité, nous ne considérerons pas la connexion de branches parallèles en OR. Nous considérons uniquement une connexion par AND, c'est-à-dire qu'un événement est déclenché uniquement lorsque tous ses événements prédécesseurs sont déclenchés.
Nous utiliserons STG pour décrire le comportement, mais avec des restrictions supplémentaires. Pour chaque lieu, le nombre d'arcs entrant et sortant est strictement égal à un chacun. En conséquence, un endroit avec des arcs entrants et sortants peut être considéré comme un arc reliant deux événements (transitions). En conséquence, le marquage se déplace le long des arcs. Comme les comportements avec plusieurs signaux ne sont pas pris en compte maintenant, les indices d'événements sont interdits, ils ne sont pas nécessaires. Les événements vides sont interdits. La situation est également interdite lorsque deux arcs inclus dans un événement sortent d'événements qui ne sont pas parallèles (un cas particulier provient du même événement). Le but de ceci est de se débarrasser des arcs qui ne portent pas de charge sémantique. Le reste est considéré comme correct (normal, en direct, sûr) du point de vue du comportement STG, en tenant compte des limitations ci-dessus. Le comportement ne contient pas de conflits CSC.
Définition 1. L'événement dans lequel l'arc entre est une conséquence de l'événement d'où sort cet arc. Inversement, l'événement d'où sort l'arc est la cause de l'événement dans lequel cet arc entre.
Définition 2. Un chemin - une séquence infinie d'événements - le résultat de changements dans l'étiquetage d'un graphique, en commençant par un spécifique. Chaque événement entre dans la séquence un nombre infini de fois. Chacune de ces entrées est unique.
Définition 3. La trace de l'événement A est le chemin dans lequel tous les événements sont soit la conséquence directe de l'événement A, soit le résultat de la fermeture transitive de la relation de la conséquence des événements par rapport à l'événement A. Le marquage initial de la trace de l'événement A est établi comme suit. Si le marquage est modifié arbitrairement, après le déclenchement de l'événement A, les marqueurs dans les arcs de sortie de l'événement A sont fixes. Ensuite, le reste des marqueurs se déplace jusqu'à ce que le mouvement des marqueurs devienne impossible sans libérer les marqueurs dans les arcs de sortie de l'événement A. Le marquage résultant est le marquage initial pour la trace de l'événement A.
Définition 4. Nous introduisons la relation d'ordre pour trois événements (A, B, C). Trois événements sont ordonnés (écrits A> B> C) si et seulement si, pour toute trace d'événement A, la première occurrence de l'événement B dans la séquence se produira toujours plus tôt que la première occurrence de l'événement C.
Remarque. L'événement A peut être parallèle aux événements B et C (ou seulement C), ou les deux événements A et B peuvent être parallèles à l'événement C.
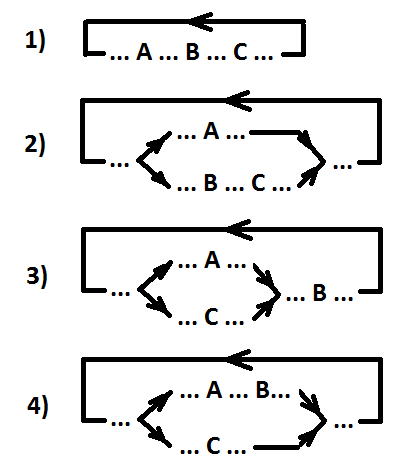
Options de localisation pour les événements ordonnés A, B et C (A> B> C).
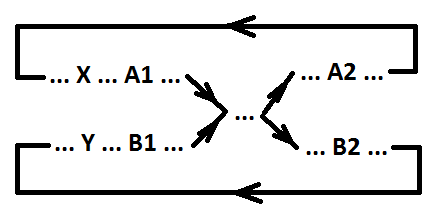
Définition 5. Le signal b (commutation B1 et B2) capte le signal a (commutation A1 et A2) par rapport aux événements X et Y (les événements X et Y sont parallèles ou coïncident) si les conditions suivantes sont remplies:
1) X> A1> A2;
2) si l'événement A2 est parallèle à l'événement X et non parallèle à l'événement Y, alors X> A2> Y;
3) Y> B1> B2;
4) si l'événement B2 est parallèle à l'événement Y et non parallèle à l'événement X, alors Y> B2> X;
5) Y> B1> A2;
6) si l'événement A2 est parallèle à l'événement Y et non parallèle à l'événement X, alors Y> A2> X.
Remarque 1. Les conditions 1, 2 et 3, 4 déterminent respectivement l'ordre de commutation des signaux a et b. Les conditions 5, 6 spécifient l'ordre de l'événement de capture B1 et de l'événement de capture A2.
Remarque 2. L'événement X peut être l'événement A1. Dans ce cas, les conditions 1 et 2 dégénèrent.
Remarque 3. L'événement Y peut être l'événement B1. Dans ce cas, les conditions 3, 4 et 5 dégénèrent.
Remarque 4. L'événement X peut être l'événement A1, et également l'événement B1 peut être l'événement Y. Dans ce cas, les conditions 1, 2, 3, 4 et 5 dégénèrent.
Maintenant, nous commençons à considérer ce qu'est un implant. L'implicant est caractérisé par des événements, à la suite desquels l'implicant change de sens.
Définition 6. Un événement, à la suite duquel l'impliquant ET (OU) change sa valeur de 1 (0) à 0 (1), nous appellerons la limite droite de l'implicant. Le signal correspondant à cet événement sera appelé mise sous tension. L'implicant s'allume.
Définition 7. Un événement, à la suite duquel l'impliquant ET (OU) change sa valeur de 0 (1) à 1 (0), nous appellerons la bordure gauche de l'implicant. Le signal correspondant à cet événement sera désactivé. L'implicant s'éteint.
Définition 8. Un implicant dans lequel deux frontières droites (ou deux gauches) ne sont pas parallèles l'une à l'autre sera appelé discontinu.
Pour l'instant, nous ne considérerons pas les implants interrompus. Nous reviendrons sur leur considération ci-dessous.
Donc, nous avons: toutes les bordures droites des implicants sont parallèles par paires les unes aux autres, ainsi que les bordures gauches des implicants sont parallèles par paires les unes aux autres.
Une propriété importante. L'implicant s'active quand au moins un événement se produit, qui est la bordure droite de l'implicant. L'implicant se désactive uniquement lorsque tous les événements qui sont les limites gauches de l'implicant se produisent.
Reste maintenant à identifier les propriétés des signaux formant l'implant.
Définition 9. Le signal inclus dans l'implant sera appelé variable.
La première propriété des variables. L'activation et la désactivation des signaux sont variables.
La deuxième propriété des variables. Pour toute variable de commutation (l'un des commutateurs est la bordure gauche de l'implicant L, l'autre est un événement X), il doit y avoir un événement - une bordure droite R du même implicant est telle que X et R sont le même événement, ou R > X> L.
La troisième propriété des variables. Pour toute variable inclusive (dont l'un des commutateurs est la bordure droite de l'implicant R, l'autre est un événement X), il doit y avoir un événement - une bordure gauche L du même implicant est telle que X et L sont le même événement, ou R > X> L.
La quatrième propriété des variables. Pour toute variable (commutation X1 et X2) qui ne s'allume ou ne s'éteint pas, il doit y avoir deux événements: une bordure gauche de l'implicant L et une bordure droite de l'implicant R telle que R> X1> L et R> X2> L . Sinon, l'implicant ne pourrait pas maintenir une valeur constante en position d'arrêt.
La cinquième propriété des variables. Pour toute paire: une variable de commutation et une variable de commutation, il doit y avoir une séquence de variables se ramassant par rapport à certaines bordures droites de l'implicant (pour différents micros, les bordures droites peuvent varier), en commençant par cette variable de commutation et en terminant par cette variable de commutation . Sinon, l'implicant ne pourrait pas maintenir une valeur constante en position de marche.
Sixième propriété des variables. Pour toute variable inclusive a, si la limite droite de l'implicant est l'événement a + (a-), alors une telle variable est incluse dans l'enregistrement de l'implicant AND (OR) avec inversion, et dans l'enregistrement de l'implicant OR (AND) sans inversion. Pour toute variable de commutation a, si la bordure gauche de l'implicant est l'événement a- (a +), alors une telle variable a est incluse dans l'enregistrement de l'implicant AND (OR) avec inversion, et dans l'enregistrement de l'implicant OR (AND) sans inversion.
La septième propriété des variables. En vertu de la quatrième propriété des variables, pour chaque variable a qui ne s'active ou ne s'éteint pas, il existe une frontière droite pour les implicants R et une frontière gauche pour les implicants L telles que R> a +> L et R> a-> L. Si R> a +> a-, alors une telle variable entre l'implicant de And avec inversion, et l'implicant de OR sans inversion. Si R> a-> a +, alors une telle variable entre l'implicant ET sans inversion, et l'implicant OU avec inversion.
Les sept propriétés listées des variables sont des propriétés nécessaires de l'implicant. De plus, ces propriétés sont suffisantes pour décrire les implants.
Remarque. La description ci-dessus de l'implant n'interdit pas la situation où une bordure gauche de l'implant peut être parallèle à une bordure droite du même implicant. La signification de ce phénomène est que, selon la vitesse des processus parallèles, un tel implant en temps réel peut ne pas être nécessaire pour la mise en œuvre du signal correspondant et en temps réel il peut ne pas s'éteindre (si la limite droite fonctionne plus tôt que la limite gauche).
Nous allons maintenant examiner comment la forme normale d'une fonction logique est construite à partir de l'implicant.
Définition 10. Si pour certains états l'implicant est en position arrêt (la valeur de l'implant ET (OU) est 1 (0)), nous disons que l'implicant couvre cet état.
Considérons un certain signal x, pour lequel nous devons calculer une fonction logique. Pour construire un DNF (CNF), il est nécessaire que les implicants ET (OU) couvrent tous les états où la fonction x est 1 (0). Dans ce cas, il est nécessaire qu'aucun de ces implicants ET (OU) ne couvre les états dans lesquels la fonction x est 0 (1). De plus, lors du calcul des fonctions logiques, il est nécessaire de prendre en compte les spécificités des circuits: les implicants doivent «se chevaucher». Autrement dit, si dans un certain état l'implicant peut s'allumer (c'est-à-dire qu'un événement peut être déclenché qui est la limite droite de cet implicant) et que la valeur de la fonction de signal x ne change pas pendant cette commutation, alors il doit y avoir un autre implicant qui couvre cet état et ne s'allume pas lorsque cet événement est déclenché.
Maintenant, nous devons clarifier trois questions. Qu'est-ce qu'un état en termes de graphique? Comment déterminer les états dans lesquels la fonction de signal x est 1 (0)? Comment déterminer les conditions que couvre l'implant?
Commençons par les états. Tout étiquetage réalisable est une condition. Puisqu'il n'y a aucun conflit CSC, chaque étiquette réalisable correspond à un état unique (réalisable). Dans les états inaccessibles, la valeur de la fonction est arbitraire et il n'est pas nécessaire de les prendre en compte. Ainsi, chaque état que nous considérons est uniquement décrit par l'étiquetage correspondant. La position de chaque marqueur est uniquement déterminée par l'arc qu'il marque. Chaque arc est associé de façon unique à une paire d'événements (ordonnés): l'événement à partir duquel l'arc sort et l'événement dans lequel l'arc entre. Ainsi, tout état réalisable est uniquement décrit par un ensemble composé de paires ordonnées d'événements.
Définition 11. Une paire d'événements désignant un arc marqué sera écrite {P, S}, où P est l'événement de cause et S est l'événement de conséquence.
Définition 12. MM sera appelé l'ensemble des paires ordonnées {P, S}, qui décrit un état réalisable.
Déterminons maintenant pour quels états la valeur de la fonction x est 1 et pour laquelle elle est 0. Soit les événements x + causés par n événements A1, A2, ..., An, et les événements x- provoqués par m événements B1, B2, ..., Bm.
La valeur de la fonction x est 1 si:
ou 1) pour chaque i de 1 à n, la paire {Ai, x +} appartient à l'ensemble MM;
ou 2) une paire {x +, S} telle que x +> S> x- appartient à l'ensemble MM;
ou 3) une paire {P, S} telle que x +> P> x- et x +> S> x- appartient à l'ensemble MM;
ou 4) une paire {P, x-} telle que x +> P> x- appartient à l'ensemble MM et il existe i de 1 à m tel que la paire {Bi, x-} n'appartienne pas à l'ensemble MM.
La valeur de la fonction x est 0 si:
ou 1) pour chaque i de 1 à m, la paire {Bi, x-} appartient à l'ensemble MM;
ou 2) une paire {x-, S} telle que x-> S> x + appartient à l'ensemble MM;
ou 3) une paire {P, S} telle que x-> P> x + et x-> S> x + appartient à l'ensemble MM;
ou 4) une paire {P, x +} telle que x-> P> x + appartient à l'ensemble MM et il existe i de 1 à n tel que la paire {Ai, x +} n'appartienne pas à l'ensemble MM.
Nous découvrons maintenant les conditions couvertes par l'implant. Soit l'implicant a n bornes gauche L1, L2, ..., Ln et m bornes droite R1, R2, ..., Rm.
L'implicant ne couvre pas l'état décrit par l'ensemble MM si au moins une des paires {P, S} appartenant à l'ensemble MM satisfait à la condition suivante: il existe i de 1 à n et j de 1 à m tels que
soit 1) Li et S sont le même événement et Rj> P> Li,
ou 2) Rj et P sont le même événement et Rj> S> Li,
ou 3) Rj> P> Li et Rj> S> Li.
Cette affirmation est vraie en vertu de la cinquième propriété des variables.
L'implicant couvre l'état décrit par l'ensemble MM si pour aucune des paires {P, S} appartenant à l'ensemble MM la condition suivante est satisfaite: il existe i de 1 à n et j de 1 à m tels que
soit 1) Li et S sont le même événement et Rj> P> Li,
ou 2) Rj et P sont le même événement et Rj> S> Li,
ou 3) Rj> P> Li et Rj> S> Li.
Cette affirmation est vraie en raison des deuxième, troisième et quatrième propriétés des variables.
Au sens figuré, un implicant couvre l'état si tous les marqueurs se trouvent entre les limites gauche et droite de l'implicant. Si au moins un marqueur est situé en dehors de ces limites, l'implant ne couvre pas cet état.
Nous avons maintenant un outil pour calculer les formes normales (ce n'est toujours pas clair, cependant, il y a encore une question avec les implants intermittents). Mais nous nous intéressons aux formes normales minimales (en tenant compte des spécificités des circuits). Avant de poursuivre, revenons à la considération des implicants intermittents. Considérons l'implicant I pour le signal DNF x (le cas avec l'implicant OR pour CNF est similaire). Supposons que les deux limites gauches des mêmes implicants L1 et L2 ne soient pas parallèles entre elles et L1> L2> x- (le cas de deux limites droites est considéré de la même manière). Ensuite, il doit y avoir deux limites droites des implicants R1 et R2 de telle sorte que pour les paires de L1 et R2 et L2 et R1, les deuxième, troisième, quatrième et cinquième propriétés des variables doivent être satisfaites. S'il y a une frontière gauche L3 parallèle à L1, alors pour la paire L3 et R2, les propriétés ci-dessus doivent également être remplies (de même, dans le cas de l'existence de frontières correspondantes, implicants parallèles aux frontières L2, R1 et R2). Mais, comme plusieurs signaux ne sont pas utilisés, il doit y avoir un implicant non discontinu avec les limites L1 et R2 (et avec des limites correspondantes parallèles, si l'un des implicants interrompus en avait). Dans ce cas, l'implicant non discontinu se compose de moins de variables et couvre tous les états couverts par l'implicant discontinu, sur lesquels la valeur de la fonction de signal x est 1. D'où la conclusion: les implicants discontinus ne sont pas des extrêmes et ils ne peuvent pas être utilisés pour calculer des fonctions minimales.
Plus d'informations sur le calcul des fonctions minimales dans la partie suivante.