Ville sans embouteillage

Chapitre deux
( lien vers le premier chapitre )

L'art de concevoir des réseaux routiers

Problèmes de transport de la ville à travers les yeux d'une personne de l'informatique

Si on me recommandait un article intitulé «L'art de concevoir des réseaux routiers», je demanderais immédiatement combien de réseaux routiers ont été construits avec la participation de son auteur. Je dois avouer que mon activité professionnelle était loin de la construction de routes et était récemment associée à la conception de microprocesseurs, où j'étais, entre autres, engagé dans la consommation de ressources de la commutation de données. Il se trouve que ma table s'est alors tenue juste en face de la fenêtre panoramique, ce qui a ouvert une belle vue sur la longue section de la route de Volgograd et une partie du troisième anneau de transport avec leurs embouteillages sans fin du matin au soir, d'horizon en horizon. Et puis, un jour, je me suis soudainement rendu compte: "Merde, car la complexité du processus de commutation de données avec laquelle je lutte avec une puce devrait exactement être similaire aux difficultés que le flux de voitures rencontre à l'intérieur du réseau de routes."
Probablement, c'était juste une vue de l'extérieur et l'application de méthodes qui n'étaient pas traditionnelles pour la zone étudiée qui m'ont permis de comprendre la cause des embouteillages et de faire des recommandations sur la façon de surmonter leur problème dans la pratique.

Alors, quelle est la nouveauté de l'approche?

Historiquement, l'objectif principal des routes est considéré comme l'opportunité qu'elles offrent de parcourir rapidement de longues distances (entre Rome et les provinces). Un tel jugement est justifié en ce qui concerne le réseau routier interurbain de niveau fédéral: les villes qu'elles relient ressemblent à de petits points rares sur l'atlas, et la plupart des voitures voyageant entre ces villes passent leur chemin sans tourner nulle part.

Cependant, il suffit de tourner plusieurs pages et d'ouvrir une carte détaillée d'une grande ville, car l'image change immédiatement: les adresses seules, où le voyage peut être commencé ou terminé, sont déjà environ dix mille, toutes sont assez densément et relativement de petite taille. Dans le même temps, des centaines de milliers de voitures peuvent être en mouvement dans les rues d'une telle ville à la fois, de plus, le but de chacune d'entre elles n'est pas seulement de remplir des routes déjà vides, mais de déplacer une personne ou une cargaison d'un point avec une adresse spécifique " X " à un point avec une adresse spécifique " Y ". Dans l'ensemble, cela signifie que le système de transport urbain doit être adapté pour résoudre efficacement le problème de l'adressage parallèle multiple . Ainsi, les fonctions du système de transport urbain deviennent encore plus similaires au réseau téléphonique ou informatique qu'au réseau routier interurbain.

Considérer le réseau routier comme un schéma de commutation pour un développeur ou un ingénieur matériel dans le domaine des technologies de transfert d'informations est une manière tout à fait naturelle de parler d'un problème, mais parmi les personnes impliquées dans la recherche sur les problèmes de transport, ce point de vue est, à ma connaissance, nouveau.

La théorie de la commutation des signaux est une science de l'ingénierie étroite et, à elle seule, bien sûr, ne suffira pas à planifier une rue séparée, un carrefour ou à prédire le comportement d'un flux de circulation sur une section droite et isolée d'une autoroute. Heureusement, les problèmes énumérés ci-dessus sont bien étudiés aujourd'hui et les méthodes développées pour les résoudre ont déjà été utilisées avec succès. La théorie de la commutation, à son tour, permet à l'architecte de se débarrasser du risque lorsque tous les éléments du réseau routier sont parfaitement exécutés, et la ville entre toujours dans un état d'effondrement des transports. Ce risque existe car l'exécution de plusieurs adressages simultanés nécessite beaucoup de ressources.
tâche fastidieuse, dont la clé d'une solution efficace n'est pas tant la largeur des rues et la commodité des échangeurs de transport, mais le choix compétent du schéma de commutation particulier que le réseau routier proposé mettra en œuvre.

A partir de ces travaux, par exemple, vous découvrirez pourquoi les réseaux de transport de type «artériel», qui sont encore souvent utilisés dans les villes modernes, sont «mauvais» et avec la croissance de la population entraîneront nécessairement des embouteillages. Un autre résultat intéressant, qui est en bon accord avec les observations, explique pourquoi l'expansion des routes à elle seule, si avant tous les embouteillages se sont produits exclusivement à proximité des échangeurs, est peu susceptible d'améliorer en quelque sorte la situation même si le nombre de voitures dans la ville reste le même.

Quand j'ai écrit cet article, il était important pour moi qu'il soit compréhensible pour l'architecte le plus ordinaire, puisse être utile à travers son travail. J'ai essayé d'initier le lecteur aux problèmes de commutation dans un langage simple, d'élaborer des critères pour évaluer dans quelle mesure un réseau routier particulier fera face à la tâche d'adressage parallèle, en utilisant des exemples de modèles, j'ai montré comment utiliser ces connaissances dans la pratique.

L'article est destiné à un large cercle de lecteurs qui connaissent un peu le cours universitaire de mathématiques et la théorie des algorithmes et sont prêts à y consacrer 1 à 5 jours.

Séparation et fusion des flux automobiles

Pour de nombreux conducteurs, il est évident que les difficultés de circulation surviennent principalement aux endroits de la route où les voitures, pour une raison ou une autre, sont obligées de changer de voie. Les exemples incluent les fourches, les rétrécissements, les zones de jonction et les routes d'accès aux autoroutes, les sections d'une autoroute où certaines voies sont bloquées par un accident ou la réparation de la route.
Dans cette section, nous tenterons de donner une description quantitative des processus qui se produisent dans de tels cas, et nous commencerons par comprendre comment les voitures sont reconstruites d'une voie à l'autre.

Deux stratégies pour reconstruire dans une rangée adjacente

Le mouvement de la circulation le long de l'autoroute présente une irrégularité naturelle: quelqu'un préfère conduire un peu plus vite, quelqu'un un peu plus lentement, entre certaines voitures, la distance diminue et devient à peine confortable pour la conduite, tandis qu'entre les autres, elle augmente tellement qu'elle permet aux voitures de s'y adapter. des voies adjacentes. L'apparition de tels écarts dans l'écoulement de la voie adjacente directement du côté du conducteur aléatoire peut être fréquente ou peu. Si, au moment où il a besoin de faire une manœuvre, il n'y a pas d'écart, le conducteur peut recourir à au moins deux stratégies comportementales:

Stratégie n ° 1
Plusieurs espaces appropriés peuvent simplement être situés à proximité de son emplacement. Si le mouvement est suffisamment dense, il est peu probable que le conducteur puisse augmenter la vitesse et rattraper l'écart nécessaire, mais ralentir un peu le mouvement et laisser le ruisseau voisin se dépasser pour égaler l'écart qui était à l'origine - il n'y aura pas de gros problème. Les coûts de cette stratégie sont évidents: le conducteur lui-même et les voitures conduisant derrière dans sa voie perdent du temps en raison de la nécessité de réduire la vitesse.

Stratégie n ° 2
Pour attendre, vous devez avoir de la patience et disposer du temps nécessaire pour cela. Une alternative peut être une tentative d'effectuer la manœuvre nécessaire «ici» et «maintenant». Selon cette idée, le conducteur donne un signe aux voitures derrière lui de la bande dans laquelle il va se déplacer. Ceux-ci, à leur tour, en réponse à son signal devraient ralentir un peu et "lâcher" en avant, les voitures se déplaçant devant elles, donnant ainsi à l'écart la taille nécessaire, se formeront dans leur flux. Les coûts de temps dans ce cas sont répartis entre les voitures de la voie où le conducteur a finalement reconstruit.

Dans la vie réelle, les deux stratégies sont impliquées en même temps: tout d'abord, le conducteur ralentit, attendant un écart relativement important dans le flux de la voie voisine, et ne fait ensuite qu'informer les voitures qui s'y déplacent de leur intention d'effectuer une manœuvre de reconstruction.

Bien sûr, les entrées, les rampes et les rétrécissements ne sont pas la seule raison du changement de voie à voie, ce qui mérite d'être rappelé lors de la conception des routes. La capacité des voitures à des vitesses plus élevées de dépasser la circulation sans hâte est nécessaire pour que la situation sur l'autoroute ne se dégrade pas en une grande file d'attente rampant à la vitesse du tracteur le plus lent. Néanmoins, le problème de la coexistence de véhicules circulant à des vitesses différentes sur la route est de nature légèrement différente et peut être séparé des problèmes abordés dans cet article, car le processus de dépassement et les réarrangements associés ne sont pas des actions forcées du conducteur qui l'obligent à se précipiter. . S'il y a du temps pour attendre, alors selon la théorie des probabilités, c'est une opportunité pratique pour effectuer une manœuvre à laisser au conducteur seul et pour cela cela n'interfère pas nécessairement avec le mouvement des autres automobilistes.

Coût d'un coup
Le comportement des conducteurs peut en réalité être très difficile, mais il est important pour nous tout d'abord que le résultat obtenu dans les conditions du modèle reste plausible: chaque mouvement forcé d'une voiture d'une voie à l'autre impose une pénalité temporaire aux participants au trafic.

Voyons maintenant comment la quantité de temps perdu dépend de la densité des voitures sur la route.

Nous considérerons le mouvement le long de chaque voie comme un ruisseau distinct. En essayant de rester à une distance confortable des voitures qui sont dans la même voie, les conducteurs réservent ainsi une partie d'une certaine longueur caractéristique d dans le flux. Laissez ρ les voitures tomber dans un flux par unité de longueur. Nous convenons d'appeler la densité de flux petite , ou, la même chose, de dire que ρ est petit si le produit ρ × d est bien inférieur à l'unité.

Au moment où le conducteur se rend compte de la nécessité de passer à la ligne suivante, la probabilité que la section de la quantité d qu'il allait y occuper ne soit pas libre, à petit ρ elle sera approximativement proportionnelle à ρ lui-même. Si l'événement décrit a réellement lieu, alors au total deux voitures en compétition pour une place connaîtront à la suite de manœuvres un certain retard dans la valeur constante moyenne δ .

En supposant que ρ est petit, la probabilité que leurs actions à ce moment affectent le mouvement des autres voitures peut être négligée. Ainsi, dans le premier ordre de petitesse par rapport à ρ , la perte de temps d'un mouvement sera α ⋅ ρ , où le coefficient α est une quantité mesurable empiriquement, en fonction de la culture, du temps, des limites de vitesse (et ainsi de suite), mais restant approximativement constant localement dans le temps et pour cette ville dans son ensemble.

L'intensité des pertes sur le site avant la sortie
Les voitures qui partent pour le congrès, avant d'arriver à la rampe (Fig. 2), doivent, parfois même plusieurs fois, être reconstruites dans la rangée adjacente à droite. Chacune de ces manœuvres rend la circulation difficile et, par conséquent, la vitesse moyenne dans le tronçon avant la sortie est sensiblement plus faible que dans les tronçons «transit» (privés des sorties, «entrées» et fourches) de l'autoroute.


fig. 2

Passer une partie du chemin à une vitesse inférieure - fait demi-tour pour les conducteurs (et leurs passagers) un temps supplémentaire consacré au voyage. En d'autres termes, la zone de l'autoroute directement adjacente à la rampe est un générateur constant de pertes temporaires.

Supposons que la vitesse moyenne de la machine ν et la densité de flux ρ à la frontière frontale de cette région soient les mêmes pour toutes les bandes.

Supposons par ailleurs que la densité ρ et le débit q sortant de la sortie (le nombre moyen de voitures entrant sur la rampe par unité de temps) soient simultanément petits, et s est le nombre de voies sur l'autoroute. Pour arriver à la sortie, le conducteur effectuera 1 à s manoeuvres de reconstruction. Si la densité de flux sur la rampe est bien inférieure à ρ , alors seule la dernière manœuvre lui coûtera pratiquement «gratuitement», tandis que le reste entraînera en tout cas des pertes de α ⋅ ρ . En moyenne, vous devrez effectuer (0 + 1 + 2 + ... + s - 1) / s = ( s - 1) / 2 manœuvres «coûteuses».

Étant donné les difficultés causées par toutes les voitures qui partent pour le congrès, nous pouvons écrire la formule de l'intensité des pertes temporaires:

I _out = q ⋅ α ρ ⋅ ( s - 1) / 2 = ( α / 2 ν ) ⋅ q ⋅ ( sρν ) ⋅ (1 - 1 / s )

La valeur p = ( sρν ) n'est rien de plus que le débit de toutes les voitures se déplaçant le long de l'autoroute dans la direction en question (le nombre moyen de voitures passant par la colonne par unité de temps). La dernière remarque nous donne l'occasion de réécrire la formule de I sous une forme plus symétrique:

I _out = ( α / 2 ν ) ⋅ pq ⋅ (1 - 1 / s )

Taux de perte dans la section adjacente de la route d'accès
La situation qui se présente sur l'autoroute derrière l'endroit où la route d'accès se connecte avec elle reprend en grande partie la situation sur le site devant le congrès, bien qu'il y ait quelques différences.
Laissez un petit flux de wagons de puissance q traverser la rampe latérale verser le trafic principal de l'autoroute (Fig. 3).


fig. 3

La rampe n'a qu'une longueur finie, donc toutes les voitures nouvellement arrivées devraient être construites bon gré mal gré dans la voie la plus à droite de l'autoroute. En conséquence, la densité de la circulation dans la voie la plus à droite est localement supérieure à la moyenne sur la route, donc certains des conducteurs décident de changer de voie pour une rangée adjacente moins occupée sur la gauche, ce qui, à son tour, conduit à une augmentation locale de la densité déjà dans la seconde bande. Ce processus de migration inter-bandes se poursuivra jusqu'à ce que la densité de l'écoulement soit nivelée sur toute la largeur de l'autoroute. En supposant que la vitesse moyenne ν soit la même pour toutes les n bandes, nous pouvons nous attendre à ce qu'à la fin des processus de migration, la puissance d'écoulement dans chacune d'entre elles augmente exactement (1 / s ) ⋅ q .

Pour voir combien ce «roque» coûte aux conducteurs, nous calculons d'abord la puissance de tous les flux de migration. Le débit de la rampe à la première voie de l'autoroute que nous connaissons déjà: il est égal à q . Pour obtenir un équilibre sous la forme d'une augmentation de (1 / s ) ⋅ q , le flux dans la deuxième voie du côté de la première doit déjà être (1 - 1 / s ) ⋅ q , de la deuxième à la troisième - (1 - 2 / s ) ⋅ q , du kième côté au ( k + 1) e - (1 - k / s ) ⋅ q . Selon la dernière formule, la capacité du flux de migration vers la voie la plus à gauche sera de (1 - ( s - 1) / s ) ⋅ q = (1 / s ) ⋅ q , comme le veut le bon sens.

Puisque nous connaissons la pénalité temporelle d'une seule reconstruction et la puissance de tous les flux migratoires, nous pouvons maintenant calculer l'intensité totale des pertes générées par ceux-ci:

I _in = α ρ ⋅ q + α ρ ⋅ (1 - 1 / s ) ⋅ q + α ρ ⋅ (1 - 2 / s ) ⋅ q + ... + α ρ ⋅ (1 / s ) ⋅ q =

α ρ q (1 + 2 + ... + s ) / s =

α ρ q ( s + 1) / 2 =

( α / 2 ν ) ⋅ q ⋅ ( sρν ) ⋅ (1 + 1 / s ).

En rappelant à nouveau que sρν est la puissance p du flux de toutes les voitures le long de l'autoroute, nous obtenons la formule de coût dans sa forme finale:

I _in = ( α / 2 ν ) ⋅ pq ⋅ (1 + 1 / s ).

Taux de perte de fourche symétrique
Dans les paragraphes précédents, nous avons constaté des pertes dues à l'interaction des flux, dont l'un était nécessairement important et l'autre était nécessairement faible. Pour démontrer l'approche de résolution de problèmes lorsque les capacités des deux flux sont comparables en ampleur, considérons un autre extrême: une fourche dans laquelle les deux directions «filles» sont également populaires pour les conducteurs (Fig. 4).


fig. 4

Pour plus de commodité, les voitures allant à droite sur la fourche seront appelées «bleues», et les voitures partant à gauche - «rouges». Au départ, les voitures des deux «couleurs» se déplacent de façon mixte, dispersées entre les 2 voies de l'autoroute. À l'approche de la jonction, les voitures rouges commencent à dériver lentement vers la gauche sur les n voies, et les bleues vers la droite sur les voies: la migration s'écoule dans les deux sens entre les voies adjacentes. Contrairement à l'exemple de la route d'accès, ces flux ne sont plus «relativement faibles». Soit dit en passant, seulement entre les deux voies centrales, il y a un échange de trafic forcé, dont l'intensité dans toutes les directions (de gauche à droite ou de droite à gauche) est égale à un quart de la puissance de l'ensemble du flux se déplaçant le long de l'autoroute des voitures. Heureusement, dans cette situation, il existe un moyen suffisant pour estimer les coûts générés. Tout d'abord, nous notons que le processus de division des voitures en «rouge» et «bleu» commence très probablement bien avant la fourche et se déroule lentement, par conséquent, d'une part, il devrait avoir peu d'effet sur la densité du trafic dans une ligne distincte, et d'autre part, effectuer la migration des flux étirés sur de longues distances, donnant ainsi la possibilité de représenter chacun d'eux comme une combinaison d'un grand nombre de flux de faible puissance (Fig. 5).


fig. 5

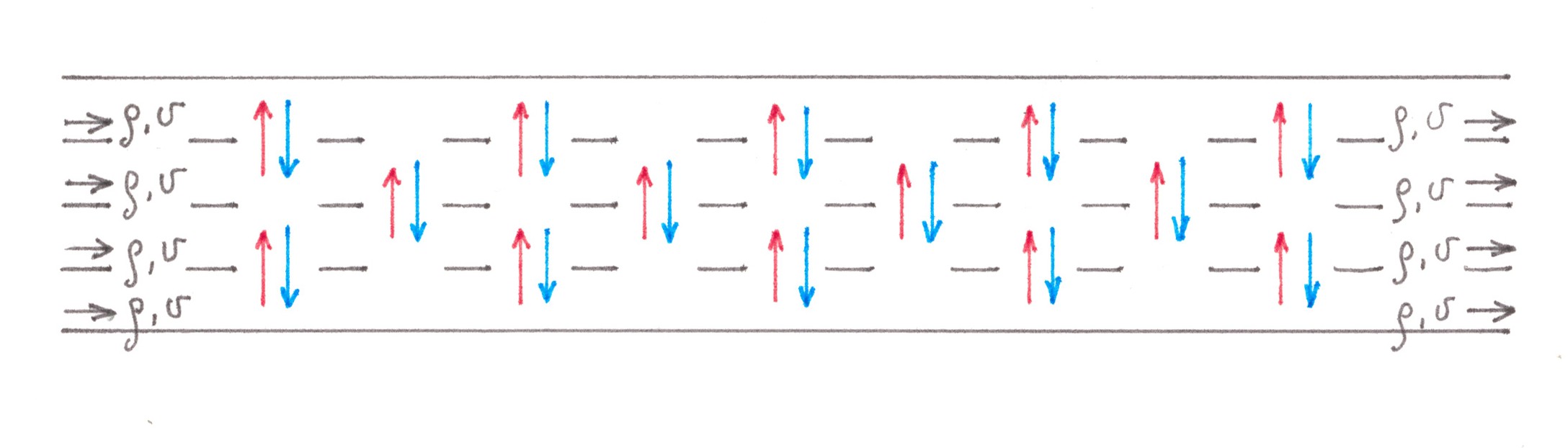
Puisque nous parlons maintenant de petits flux, quoique en plus grand nombre, rien ne nous empêche de réduire le problème considéré à des problèmes déjà résolus. Divisez mentalement l'autoroute au centre en deux parties égales, puis connectez-les ensemble avec un grand nombre de routes jumelées à voie unique, permettant aux voitures rouges d'atteindre le côté gauche et aux voitures bleues à droite (Fig.6). En raison de la symétrie évidente, lors du calcul des pertes générées, nous pouvons nous concentrer sur des machines de n'importe quelle couleur, par exemple le bleu, et au final, simplement doubler le résultat.


fig. 6

Donc, la vitesse ν et la densité ρ soient les mêmes pour toutes les voies et restent constantes dans toute la zone où les voitures sont séparées par des couleurs.Dans ce cas, le débit de toutes les voitures circulant sur l'autoroute sera:

p = 2 sρv .

Soit q ₁ , q ₂ , ... q _m désignent les flux de voitures bleues se déplaçant le long de cavaliers imaginaires vers la moitié droite de l'autoroute. Supposons que peu de temps avant le site de séparation dans chaque voie de l'autoroute, les deux couleurs soient représentées avec des proportions égales de 50%, ce qui implique qu'au total
q ₁ + q ₂ + ... + q _m sont égaux à sρv / 2, qui est p / 4.

Pertes générées par le flux q_i , en raison de sa petitesse, nous pouvons calculer par la formule:

I _i =I _out +I _in = (α/ 2ν)⋅(p/ 2)⋅ q _i (1 - 1 /s) + (α/ 2ν)⋅(p/ 2)⋅ q _i (1 + 1 /s) = (α/ 2ν)p q _i

Addition de la dernière expression sur touti, Trouver la perte générée uniquement les voitures bleues:

I _bleu = ( α / 2 ν ) ⋅ p ⋅ ( q ₁ + q ₂ + ... + q _m ) = ( α / 2 ν ) p ² /4.

perte complète, comme déjà mentionné, est doublée et la quantité deux fois:

I _div = ( α / 2 ν ) p ² /2.

Analyse des formules obtenues
Si l'on sépare l'intensité Ic'est-à-dire le temps total perdu par seconde par le nombre de flux latéraux q , qui est par définition égal au nombre de voitures connectant ou quittant le trafic sur l'autoroute en une seconde, nous obtenons les pertes moyennes générées par une telle voiture:

i _in = I _in / q = ( α / 2 ν ) ⋅ p ⋅ (1 + 1 / s )

i _out = I _out / q = ( α / 2 ν ) ⋅ p ⋅ (1 - 1 /s ) La

chose la plus importante dans ces formules est peut-être la proportionnalité directe entre le flux de puissance des voitures sur l'autoroute p et les coûts unitaires i . Tout ressemble à une voiture cherchant à rejoindre, ou vice versa - à quitter le flux du mouvement principal, causant ainsi des dommages constants à chaque conducteur à proximité.

La deuxième observation, intéressante et très inattendue, concerne l'effet extrêmement faible sur l'intensité des pertes générées du nombre de voies à proximité de l'autoroute juste à côté de la jonction. Comme vous pouvez le voir, en regardant la formule pour I _out , le congrès est généralement le moins cher pour une route à voie unique ( s = 1, i _out = 0), et les difficultés causées par la route d'accès adjacente pour une autoroute à trois voies et une autoroute à six voies ne diffèrent que de

100% ⋅ [(1 + 1/3) - (1 + 1/6)] / (1 + 1/3) = 12,5%.

Si nous prenons en compte que chaque voiture qui a déjà rejoint le trafic sur l'autoroute devra éventuellement la quitter, il semble tout à fait légal d'utiliser la valeur unifiée i _av = ( i _in + i _in au lieu de i _in et i _out ) / 2 = ( α / 2 ν ) ⋅ p .



Malgré l'absence dans la formule pour i _{av d'} une dépendance explicite du nombre de voies, il faut se rappeler que sa conclusion (voir les hypothèses pour I _in et I _out ) repose fortement sur l'hypothèse d'une faible densité de voitures sur la route, il est donc peu probable de donner des résultats satisfaisants, étant appliqué à une autoroute trop étroite avec trop de trafic.

Constatations préliminaires
Dans les zones proches des carrefours, le trafic se produit inévitablement, prenant du temps aux conducteurs, réduisant la vitesse moyenne, ce dernier conduit à une augmentation de la densité des voitures et, par conséquent, à l'apparition possible d'embouteillages. Les coûts de temps associés à la séparation et à la fusion des flux automobiles seront appelés commutation.

Les pertes d'un type similaire sont présentes d'une manière ou d'une autre dans n'importe quel schéma de commutation: qu'il s'agisse d'un réseau téléphonique ou informatique, d'un microprocesseur multicœur ou d'un service de distribution de courrier.

Lorsqu'un conducteur rejoint, ou inversement, quitte la circulation sur l'autoroute, les coûts de commutation occasionnés par ses actions sont proportionnels à la puissance du flux de voitures observé à ce moment sur l'autoroute.

Pour réduire les pertes de commutation dans toute la ville, il est nécessaire de considérer attentivement le réseau routier qui y est mis en œuvre au stade de la conception. Un peu plus tard, nous analyserons cette tâche en détail, mais certaines recommandations évidentes peuvent être répertoriées maintenant:

1. les pertes de commutation sont proportionnelles à la capacité de débit sur l'autoroute - il n'est pas nécessaire d'agrandir les routes sans la nécessité, deux petites autoroutes sont deux fois plus bonnes qu'une grande;
2. les pertes de commutation sont proportionnelles à la puissance des flux latéraux - il convient de concevoir le réseau de sorte que le conducteur ait dû se dérober le moins de fois possible pendant son trajet;
3. l'interférence mutuelle causée par les conducteurs des flux principal et latéral devrait devenir plus petite à l'échelle de la ville si vous essayez d'empêcher des itinéraires qui ne se chevauchent que sur une courte section de la piste dans un flux.

Conditions économiques préalables à l'existence des villes.
Modèle de ville d'accès uniforme

La première chose à entreprendre pour planifier (ou replanifier) ​​le système de transport urbain est peut-être d'essayer de déterminer le type de migration dont la ville a réellement besoin maintenant et comment ses besoins évolueront à l'avenir.

Une telle analyse peut être effectuée si vous divisez d'abord la ville en zones territoriales pas trop grandes, mais pas trop petites, puis pour chaque paire de telles zones, indiquez le nombre approximatif de déplacements d'un côté ou de l'autre dont leurs habitants ont besoin à un moment ou à un autre. du jour. En plaçant les prévisions faites dans un tableau carré, vous recevrez ainsi une matrice des besoins migratoires des habitants de la ville.

C'est pour cette matrice qu'il vaut alors la peine de chercher un réseau qui permette aux conducteurs et aux passagers de passer le moins de temps possible sur un trajet séparé et qui demande aux autorités de la ville le moins de ressources possible pour leur construction.

En ce qui concerne les villes existantes, il est important ici de ne pas se tromper et de ne pas remplacer le nombre de voyages dont les gens ont vraiment besoin par le nombre de voyages qui ont été historiquement établis sous l'influence de certains obstacles ou difficultés au moment du travail de conception. Probablement, le réseau de transport de Berlin «avant» et «après» la chute du mur de séparation peut servir d'illustration la plus frappante de ce qui a été dit.

Cette section traitera principalement des questions humanitaires dans lesquelles je ne suis pas un spécialiste, mais je pense que les discuter en tant qu'amateur est néanmoins plus correct que de simplement éviter le problème.

Pour mieux représenter les besoins migratoires de la population, il convient de commencer par la question fondamentale: «Pourquoi les villes ont-elles vraiment besoin et quelle fonction utile remplissent-elles?» .

Essayons d'y répondre non pas en tant que résidents ordinaires des villes (et des villages), mais du point de vue de la personne responsable du processus d'urbanisation dans un État vaste et développé. De ce point de vue, il n'est plus important de savoir quelles motivations historiques faisaient autrefois tant de gens entassés dans un petit morceau de terre, ou les raisons pour lesquelles elles continuent de le faire maintenant, il est important - quel effet économique crée des villes d'une taille ou d'une autre et pour en raison de quels mécanismes cet effet est obtenu.

À mon avis, la principale raison de l'existence des grandes villes est, d'une part, l'opportunité pour les entreprises technologiques de trouver des employés de professions rares, et d'autre part, l'opportunité pour les personnes ayant maîtrisé des professions rares de vendre leurs services à des entreprises intéressées à des conditions compétitives. Dans une petite ville (non spécialisée), la production de nombreux biens et services est soit tout simplement impossible, soit met les entreprises technologiques et leurs employés en train de la mettre en otage mutuelle, sans donner à l'une ou à l'autre aucune alternative.

Par exemple, prenez le métier pas si rare d'un professeur d'école de littérature. Selon les statistiques, leur besoin est d'environ 1 enseignant pour 1 000 habitants. Dans une école ordinaire, 3-4 personnes enseignent la littérature. Le choix d'un emploi pour un professeur de littérature peut être qualifié de compétitif s'il existe au moins 4 à 5 écoles secondaires dans sa ville, qui, en termes de population, est d'environ 15 000 personnes.

Apparemment, les personnes ayant une spécialité en ingénierie se sentent à l'aise sur le marché du travail dans les villes comptant au moins 100 000 habitants. Bien sûr, il existe également de telles professions, dont la demande n'apparaît que dans les villes d'un million d'habitants, mais le sens économique de plusieurs millions de villes reste pour moi un mystère.

Après tout ce qui précède, deux hypothèses semblent assez motivées (dont la validité, cependant, n'affecte pas la vérité du contenu principal de l'article):

1. les voyages les plus fréquents que l'adulte moyen a besoin de parcourir sur des distances qui capturent 4-5 des emplois les plus prometteurs pour lui;
2. pour une partie importante de la population qui possède les professions rares et les plus économiquement précieuses, la distance des déplacements les plus fréquents pourrait bien être comparable au rayon de la ville.

Pour mieux refléter les hypothèses 1) et 2), dans mes exemples, j'utiliserai souvent le modèle de la ville à «accès uniforme», en supposant que la puissance des flux de déplacements demandés est la même entre les deux quarts de celle-ci, ou, en d'autres termes, dans toutes les cellules de la matrice les besoins migratoires valent le même nombre positif. Si vous regardez au hasard les enregistrements de voyages effectués dans une telle ville pendant la journée, alors pour le prochain voyage marqué, tous les quartiers auront les mêmes chances d'être le début de ce voyage et de le servir de fin, et il n'y a pas de relation entre la position de la «initiale» et de la «finale» »Les trimestres ne doivent pas être observés.

Réseaux de topologie de réseau simple

Essayons d'appliquer les idées décrites dans les paragraphes précédents à certains types de plans de ville tirés de la vie.

Ville linéaire
Les premières grandes colonies se sont établies principalement le long de la côte, dans des zones d'une mince bande de terre entre la mer et les falaises, ou le long des sentiers de routes très fréquentées, de sorte qu'au cours de leur croissance, elles ont acquis des frontières étroites et allongées. Beaucoup de ces colonies ont survécu à ce jour, conservant leur forme allongée et se transformant en villes modernes (illustration ci-dessous).


(zone isolée de Rio de Janeiro, auteur inconnu)

Souvent, dans une telle ville, il n'y a qu'une seule route large autour de laquelle elle est construite. Supposons que chaque quartier (zone de division territoriale) génère un flux de déplacements d'une seule capacité, de tous ces quartiers - n , et que la ville elle-même obéit au modèle de migration «d'accès uniforme».


fig. 7

Essayons de trouver pour les conditions énumérées ci-dessus comment le temps de trajet moyen et la surface de route requise changent avec l'augmentation de n .

Donc, laissez tous les quartiers avoir la même forme et la même taille, et leur nombre augmente de λ (lambda) fois. De toute évidence,

• la longueur de la route principale augmente d'un facteur λ .

En vertu du modèle adopté «d'accès uniforme», 50% des trajets qui ont commencé dans la moitié droite de la ville se terminent dans sa moitié gauche (exactement le contraire), donc, avec une augmentation du nombre de quartiers d'un facteur λ, la puissance du ruisseau traversant le centre de la ville augmentera également de λ fois Un raisonnement similaire avec la même conclusion sera vrai si, au lieu du milieu, nous prenons un point quelconque divisant la ville dans un rapport donné (1: 3, 2: 5), ce qui implique que

• le flux de puissance des voitures le long de la route principale augmente d'un facteur λ .
• le nombre de voies de la route principale nécessaires dans chaque section augmente d'un facteur λ .

Plus ou moins évident que la durée moyenne du voyage, et avec elle

• le temps de trajet net consacré à parcourir la distance augmente d'un facteur λ .

Il ne nous reste plus qu'à calculer combien de fois le temps perdu en raison des coûts de changement de poste en un seul voyage augmentera. Dans chaque quartier, un flux latéral de puissance unitaire entre et sort, ce qui génère ensemble des pertes d'intensité temporaires:

I = I _in + I _out = ( α / 2 ν ) p ⋅ 2,

où p est le débit sur la route principale. Nous savons déjà que le nombre de trimestres et le débit sur la route principale croissent comme λ , donc les pertes de temps totales générées par le réseau augmentent d'un facteur ² . En revanche, le nombre de déplacements générés par le réseau, entre lesquels toutes ces pertes se répartissent, augmente d'un facteur λ , d'où l'on obtient que

• le temps de trajet net perdu en raison des coûts de commutation augmente d'un facteur λ .

Collectons tous les résultats dans une seule plaque:

Topologie linéaire
Nombre de points d'adresse (trimestres) de capacité unitaire ............................... n
La superficie totale des routes ............................................... ........................................ O ( n ² )
Temps de voyage pur
dépensé pour couvrir la distance .............................................. ..... O ( n )
Temps de voyage pur
perdu en raison des coûts de changement ............................................ ......... O ( n )
Le nombre de nœuds de commutation ............................................... .................................... O ( n )
Le nombre de nœuds de commutation, en tenant compte de la puissance des flux latéraux ..................... O ( n )

Notation utilisée: " y = O ( x )", signifie que les quantités x et y sont fonctionnellement dépendantes, et lorsque x croît sans limite, le rapport x / y tend vers un nombre fini non nul.

Cell City
La deuxième méthode de planification, assez courante, consiste à disposer les blocs sous la forme d'une matrice rectangulaire, semblable à la façon dont les morceaux portionnés sont placés dans une barre de chocolat.

Nous acceptons d'appeler ces villes «cellulaires».


(Los Angeles, photo: Stepanov Glory)

La figure 8 montre un schéma de la ville cellulaire, composée de n (en tenant compte des "moitiés") des quartiers, formant ensemble un carré régulier. Les quartiers sont séparés les uns des autres par un total de √ n routes, allant conditionnellement d'ouest en est, et √ n autres routes, s'étendant du sud au nord. Au total, ces routes forment des intersections √ n × √ n , chacune pouvant être réalisée comme une intersection de feux de circulation, ou mise en œuvre à travers un pont routier et des viaducs.


fig. 8

Que le trafic dans les rues soit à sens unique ou à double sens, tout trajet du point «A» au point «B» dans une ville à damiers peut être effectué le long d'un itinéraire qui ne traverse pas plus de deux rues et ne nécessite pas plus d'un tour à l'intersection. cher.

Supposons que, comme dans l'exemple précédent, chaque trimestre génère un flux de déplacements de capacité unitaire et que les besoins migratoires de la population soient décrits par le modèle de «l'accès uniforme». Calculons maintenant, pour la ville cellulaire, les lois par lesquelles le temps de trajet moyen et la consommation de ressources de la construction d'un réseau routier avec une augmentation du nombre de trimestres changent.

Si le nombre de trimestres augmente d'un facteur λ , alors:

• la superficie de la ville augmente en λ fois, et ses dimensions linéaires tout en conservant les proportions -
  en √ λ ,
• la longueur moyenne du trajet et le temps net pour parcourir la distance, étant proportionnels aux dimensions linéaires, augmentent √ λ fois,
• le nombre de rues et le nombre de quartiers adjacents à une rue augmente √ λ fois,
• la puissance du flux de trafic, étant proportionnelle au nombre de quartiers avec lesquels le flux est «en contact» (une explication de ce fait sera donnée plus loin), augmente de √ λ fois,
• la superficie requise de toutes les routes augmente en tant que (nombre de rues) × (longueur d'une rue) × (puissance du flux routier) = √ λ ⋅ √ λ ⋅ √ λ = λ √ λ

Les flux latéraux sont divisés en ceux qui vont de ou vers les quartiers et les flux de trafic qui passent d'une rue à l'autre à leurs intersections. Le premier, selon les conditions, reste toujours égal à l'unité, après le second, si l'on tient compte du fait qu'il y a beaucoup plus de quartiers dans la ville que de quartiers sur une seule rue, presque tout le trafic qui se déplace le long de celle-ci arrive ou sort de la rue. En conséquence, le changement de l'ampleur des flux latéraux du second peut être estimé par la formule (changement de la puissance du flux de la rue) / (augmentation du nombre d'intersections sur une seule rue) = √ λ / √ λ = 1. L'égalité du dernier rapport à la constante suggère que ces flux ne changent pas spécialement avec une augmentation du nombre de trimestres, par conséquent, l'augmentation des coûts de commutation générés par le réseau dans son ensemble sera: (augmentation du nombre total de trimestres + intersections) × (variation de la valeur du flux sur une seule rue) = λ √ λ . Puisque la puissance du flux de déplacement généré par tous les trimestres a augmenté en λ , alors

• le temps de trajet net perdu en raison des coûts de changement augmente de √ λ

Imaginez le résultat sous la forme d'une tablette:

"Topologie cellulaire"
Nombre de points d'adresse (trimestres) de capacité unitaire ............................... n
La superficie totale des routes ............................................... .................................... O ( n √ n )
Temps de voyage pur
dépensé pour couvrir la distance .............................................. ... O (√ n )
Temps de voyage pur
perdu en raison des coûts de changement ............................................ ....... O (√ n )
Le nombre de nœuds de commutation ............................................... .................................... O ( n )
Le nombre de nœuds de commutation, en tenant compte de la puissance des flux latéraux ..................... O ( n )

En comparant les réseaux linéaires et cellulaires, il est difficile de ne pas remarquer que l'augmentation des ressources nécessaires à la construction et le temps consacré à un voyage avec la croissance de la ville pour le premier réseau est beaucoup plus rapide que pour le second. Par exemple, une ville cellulaire sur 100 quartiers nécessite 10 fois moins d'asphalte et un trajet à travers elle nécessite en moyenne 10 fois moins de temps que ce qui est nécessaire dans une ville linéaire de même taille. Ainsi, il est logique d'utiliser des réseaux routiers à topologie linéaire uniquement dans les très petites villes.

Si pendant un certain temps vous oubliez l'existence de coûts de commutation, la topologie cellulaire peut être considérée comme un moyen idéal pour concevoir des réseaux routiers, car elle donne une estimation O asymptotiquement optimale à la fois pour la longueur moyenne du trajet et la zone de route requise. En effet, pour tout emplacement plus ou moins «compact» de la ville (avec un accès uniforme), la durée du trajet ne croîtra pas plus lentement que la racine carrée de sa superficie, qui est généralement directement proportionnelle à la population. En conséquence, nous obtenons tout de même O (√ n ).

Le fait qu'un itinéraire typique dans la ville cellulaire longe un «coin» plutôt qu'une ligne droite, donne en principe le droit de chercher de meilleures façons de planifier les villes, mais 20% d'économies (c'est combien vous pouvez gagner à la limite si les voitures apprennent à traverser les murs) est peu probable un jour, ils forceront les architectes à abandonner la disposition rectangulaire des rues et des routes.

La limite inférieure possible du coût de construction (et d'entretien) du réseau peut être obtenue en se rappelant que chaque voiture réserve une partie de la voie pour son déplacement, par conséquent, la superficie totale des routes est proportionnelle au produit du temps de trajet moyen (durée moyenne du trajet) par le nombre de voitures dans la ville : O (√ n ) × O ( n ) = O ( n √ n ) (comparer avec le tableau pour la ville cellulaire).

Si nous parlons de la quantité de temps perdue en voyage en raison des coûts de commutation, alors, de manière surprenante, sa relation avec la durée nécessaire pour couvrir la distance ne dépend pas asymptotiquement du nombre de quartiers individuels dans une ville cellulaire ou linéaire (O (√ n ) / O (√ n ) = O (1), O ( n ) / O ( n ) = O (1)). En d'autres termes, le pourcentage de temps perdu en voyage à cause des changements d'événements dans la grande ville et la petite sera le même. De cela, nous pouvons conclure que, s'il n'y avait pas de problèmes sérieux avec les coûts de changement dans une petite ville (disons, ils s'élevaient à 10-20%), alors dans une grande ville, ils ne devraient toujours pas être observés, et s'ils l'étaient, alors eux-mêmes ils n'iront nulle part, peu importe la façon dont la ville s'est développée et agrandie.

Puisque nous ne savons pas laquelle des alternatives est vraie (ou plutôt, nous savons que des problèmes de circulation automobile existent dans les grandes villes), il vaut la peine d'essayer d'améliorer la topologie de la ville cellulaire afin que les coûts de commutation y diminuent au moins d'un temps constant.

Exemples utiles de réseaux irréalistes

Voyons si la topologie cellulaire suit les recommandations que nous avons développées en analysant la commutation des flux sur l'autoroute.

1) N'agrandissez pas les routes sans en avoir besoin.
- Oui. Le trafic est réparti sur de nombreuses routes (comparer avec Linear City).

2) Évitez de créer des conditions lorsque vous devez effectuer un grand nombre de virages en un seul voyage.
- Oui. Tout voyage sera très probablement effectué le long d'un itinéraire ne nécessitant qu'un seul virage dans les rues de la ville.

3) Évitez les situations lorsque vous voyagez sur une section de la route, dont les itinéraires n'ont qu'une petite section du chemin commun.
- Ici, peut-être, il y a quelque chose à travailler. Malgré le nombre minimum de virages par trajet, son itinéraire dans le cadre du flux de la route principale passe par un grand nombre de nœuds de commutation (O ( n )), dans chacun desquels un temps précieux est perdu.

La dernière remarque incite à enquêter sur la question suivante: «Quelle est la valeur minimale du nombre moyen de nœuds de commutation par lesquels un trajet doit passer au sein d'un réseau routier reliant n blocs?»

La tâche de recherche d'un tel réseau n'a de sens, bien entendu, qu'à la condition que le nombre de flux combinés ou partagés par un nœud de commutation soit préalablement limité par le haut par une certaine valeur fixe. Sinon, vous pouvez toujours présenter un réseau routier avec n points d'adresse et une seule méga-jonction.


(auteur inconnu)

Il est beaucoup plus facile d'étudier le problème réel s'il était auparavant possible de révéler au moins une partie des modèles à l'aide d'exemples de modèles simples, voire pas du tout réalistes. Suivant cette logique, nous oublierons temporairement les limites géométriques de la construction d'une route permettant aux voyageurs de parcourir des distances, en concentrant toute leur attention sur la façon dont les réseaux abstraits résolvent le problème d'adressage parallèle. En ce qui concerne les nœuds de commutation, nous supposerons pour l'instant que chacun d'eux divise le flux en deux parties (le nœud de division) ou combine deux flux en un.


fig. 9

Adresse arbre
Supposons que nous avons un départ adresse au point où tout commence, sans exception, Voyage, et même n finition adresse les points où ils se terminent (figure 9) avec une probabilité égale.

Il est nécessaire de construire un réseau de transport qui permette aux déplacements de passer par le moins de nœuds de commutation possible.

La solution évidente (pour les programmeurs), qui se demande ici, est d'utiliser un arbre binaire équilibré, en même temps, vous devez placer un seul point de départ en haut de l'arbre et placer les n derniers points d'arrivée un dans chacune de ses feuilles (Fig.10). Le réseau construit de la manière décrite sera appelé arbre d'adresse directe.


fig. 10

En changeant les directions de tous les flux à l'inverse dans l'arbre d'adresse direct, nous obtenons ainsi l'arbre d'adresse inverse, dont le but est de connecter n points de départ avec une seule arrivée.

Dans les cas où n est une puissance de deux, toute route à l'intérieur de l'arborescence d'adresses passe exactement par les noeuds de commutation log ₂ n , ce qui est sans aucun doute (asymptotiquement) inférieur au même indicateur pour un réseau avec Cellulaire (O (√ n )), ou Linéaire ( O ( n )) topologie.

Les deux types de réseaux logarithmiques les plus simples
En utilisant des réseaux "arborescents" comme blocs de construction, il n'est pas difficile de généraliser la solution précédente au cas où il y a plus d'un point de départ, mais -k . Il existe deux façons simples de procéder.

La première façon consiste à utiliser l'arborescence d'adresses inverse pour collecter d'abord les itinéraires de tous les trajets dans un flux commun, puis, à l'aide de l'arborescence d'adresses directe, diviser ce flux en sous-flux, chacun adressé à sa destination (réseau en haut sur la figure 11). )


fig. 11

Si k et n sont des puissances de deux, à la fin, tout itinéraire passe exactement par les nœuds de commutation log ₂ k + log ₂ n . Réseaux construits selon l'algorithme qui vient d'être décrit, nous acceptons d'appeler (unidirectionnel) Logarithmique avec fusion préalable .

La deuxième façon de résoudre le même problème peut être obtenue en inversant dans la première solution l'ordre des opérations de fusion et de séparation. Son implémentation est la suivante: pour chaque point de départ, créez un ensemble unique de doublons imaginaires de tous les points d'adresse d'arrivée, puis connectez-le à ces doublons (pas du tout imaginaires) avec une arborescence d'adresses directe.

Pour achever la construction du réseau, il ne reste plus qu'à connecter maintenant chaque point d'arrivée avec une arborescence d'adresses inversée avec k doublons imaginaires (le réseau du bas sur la Fig. 11).

Chaque fois que n et k sont des puissances de deux, le nombre de nœuds de commutation sur le chemin de n'importe quelle route au sein du réseau nouvellement construit sera à nouveau égal à log ₂ k + log ₂ n . Nous acceptons d'appeler des réseaux de ce type (unidirectionnel) Logarithmique avec séparation préalable .

Transformation de réseaux unidirectionnels en réseaux symétriques
En général, les réseaux unidirectionnelsnous appellerons n'importe quel réseau si les points d'adresse connectés par lui sont strictement divisés en début et fin. Par défaut, pour les réseaux unidirectionnels, on supposera qu'il fournit au moins une route de déplacement possible de tout point de départ à tout point d'arrivée.

En plus d'un voyage de toute une vie, il est difficile de citer des exemples où certains points d'adresse ne serviraient d'itinéraires que le début, et d'autres - ne pourraient être que leur fin. Nous rapprocherons notre raisonnement de la réalité si nous incluons également des réseaux dans lesquels deux points d'adresse sont connectés par des itinéraires dans les deux sens. Nous acceptons d'appeler de tels réseaux symétriques .

En fait, il n'y a pas de fossé idéologique entre les réseaux unidirectionnels et symétriques: chaque réseau symétrique peut être utilisé comme un réseau unidirectionnel, et chaque réseau unidirectionnel, connectant initialement un nombre égal de points de départ et d'arrivée, peut être converti en un réseau symétrique (Fig.12).


fig. 12

Les figures 13a et 13b montrent les formes "symétriques" du réseau logarithmique avec fusion préliminaire et du réseau logarithmique avec séparation préliminaire. Leurs exemples montrent la possibilité fondamentale de connecter n blocs avec ce type de réseau, dans lequel le nombre de nœuds de commutation visités au cours d'un voyage sera proportionnel au logarithme du nombre de blocs dans la ville.


fig. 13 a


fig. 13 b

Estimation précise du fond
A ce jour, une riche collection de réseaux a déjà été accumulée avec diverses fonctions en fonction du nombre moyen de nœuds visités au cours du voyage sur le nombre de points d'adresse dans la ville. Néanmoins, nous ne savons toujours pas à quel point ce nombre peut être faible en principe pour un nombre donné de trimestres. La borne inférieure de sa valeur peut être obtenue en utilisant l'approche informationnelle.

En fait, même si un certain réseau routier relie n points d’adresse et que les besoins migratoires de la population sont tels que tout voyage, quel que soit son point de départ, a une chance égale de se terminer n’importe où dans la ville.

Pour résoudre le problème prévu, nous générerons un message d'information auxiliaire, en suivant cette recette: pendant une longue période, nous collecterons les enregistrements de tous les voyages qui ont un point fixe au début, et dans un ordre aléatoire, nous noterons les adresses auxquelles ces voyages se sont terminés. Le message résultant sera une séquence aléatoire composée des noms de n points d'adresse de la ville.

Une façon de transmettre ce message à Mars consiste à coder d'abord tous les noms avec des mots binaires de la même longueur, transformant ainsi le message d'origine en une séquence de zéros et de uns, puis d'envoyer la séquence résultante via un canal de communication numérique. Puisque pour un codage distinct, l'ensemble nSi des noms binaires de longueur log ₂ n sont requis , alors la longueur du message numérique sera:

(nombre d'enregistrements) × log ₂ n caractères.

La chose la plus intéressante est que selon la théorie de l'information, quel que soit l'algorithme de codage utilisé, il est tout simplement impossible de transmettre le même message en moyenne avec un plus petit nombre de caractères binaires.

Une alternative à la transmission directe des noms codés des points d'extrémité peut être une méthode dans laquelle, pour chaque trajet, il est indiqué dans laquelle des directions possibles a tourné son itinéraire à la prochaine bifurcation de la route. Selon nos hypothèses, toutes les fourches du réseau ne peuvent être que doubles, par conséquent, pour indiquer la direction dans chaque cas, exactement 1 bit est requis. Quiconque possède une carte de la ville et connaît le point de départ, la chaîne de bits adoptée sera suffisante pour tracer chaque itinéraire et restaurer la séquence d'origine de leurs destinations. Si le nombre moyen de fourches (nœuds de division) visités au cours d'un trajet est de x , la longueur du message binaire avec la nouvelle méthode de codage sera: (nombre d'enregistrements) × x.

Comme cela a été dit précédemment, une nouvelle méthode de codage ne peut pas être plus efficace que la méthode de transfert direct d'adresses binaires, donc: (nombre d'enregistrements) × x ≥ (nombre d'enregistrements) × log ₂ n , d'où:

x ≥ log ₂ n .

Bien que la dernière inégalité ait été initialement déduite pour un groupe de déplacements ayant un point de départ fixe commun, son apparence s'est révélée indépendante du choix spécifique de ce point, nous avons donc le droit d'étendre immédiatement le résultat à tous les déplacements dans la ville, obtenant ainsi la première partie de l'estimation souhaitée:

P1 ) Pourvu que chaque nouveau voyage ait une chance égale de se terminer par npoints d’adresse de la ville, le nombre moyen de nœuds de division par itinéraire ne peut être inférieur à log ₂ n .

En tournant mentalement l'horloge en arrière, vous ferez de chaque point de terminaison de voyage le point de départ et de chaque nœud de division de réseau binaire un nœud de fusion binaire. Cette petite astuce vous permet d'obtenir automatiquement la deuxième partie manquante de l'estimation de P1:

P2 ) À condition que chaque voyage terminé ait des chances égales de commencer à l'un des n points d'adresse de la ville, le nombre moyen de nœuds de fusion par itinéraire ne peut pas être inférieur à log ₂ n .

Si nous rappelons l'existence d'un réseau logarithmique avec fusion préliminaire et d'un réseau logarithmique avec séparation préliminaire, nous obtenons immédiatement deux exemples de réseaux qui sont optimaux en termes de nombre de nœuds de commutation, qui, en moyenne, sont visités à l'intérieur d'eux pendant un voyage. Voyons si cette qualité les aide à réduire l'intensité des pertes de commutation générées.

Coûts de commutation dans les réseaux logarithmiques

Si nous comparons les réseaux avec une fusion et une séparation préliminaires, le premier semble beaucoup plus attrayant en raison de sa simplicité. Malheureusement, cette simplicité a aussi un revers à la médaille: la combinaison de toutes les routes en un seul flux contredit la recommandation i1 , devenant ainsi une cause potentielle de pertes de temps importantes. Un réseau avec séparation préliminaire semble suivre les recommandations i1 - i3 , cependant, à en juger par la figure 13b, il a tendance à augmenter rapidement le nombre de bords de route et de nœuds de commutation utilisés. Cette dernière qualité peut rendre les réseaux de ce type trop coûteux pour une utilisation pratique.

Nous analyserons ces problèmes plus en détail. Pour commencer, nous convenons que la ville est soumise au modèle de migration d'accès uniforme et que le flux de déplacements généré par l'un de ses points d'adresse a une capacité unitaire.

Pertes dans un réseau avec fusion préliminaire
Dans la figure 14, vous pouvez voir un diagramme des flux résultant des dispositions indiquées au sein du réseau avec fusion préliminaire.


fig. 14

Il m'a semblé commode de représenter le réseau sous sa forme unidirectionnelle, impliquant que chaque point de départ et d'arrivée, non signé avec les mêmes numéros, signifie en fait le même point d'adresse dans la ville.

Sur la base du diagramme, nous calculons l'intensité des coûts de commutation générés dans le réseau. Commençons par la moitié gauche, où à travers l'arborescence d'adresses inversée, toutes les routes sont collectées dans un flux. Chaque nœud de commutation dans cette partie du réseau représente l'endroit où deux autoroutes unidirectionnelles fusionnent en une (Fig. 15).


fig. 15

Si, au départ, chacune des routes est chargée efficacement, après leur unification, il n'est pas nécessaire de réduire le nombre de voies, par conséquent, il ne devrait pas y avoir de réduction associée des coûts de commutation.

Supposons qu'un flux de puissance unitaire soit déjà suffisant pour remplir efficacement la route sur au moins deux voies. Dans ce cas, nous arrivons à une conclusion plutôt inattendue: l'union des flux de voitures à l'intérieur du réseau logarithmique avec la fusion préliminaire se produit absolument «gratuitement», sans causer de pertes temporaires.

Calculer les coûts qui surviennent dans la moitié droite droite n'est pas beaucoup plus difficile. Cette partie du réseau est un arbre d'adresse directe, dont chaque nœud est une fourche symétrique dans les routes que nous avons déjà étudiées. Lorsque la puissance de l'écoulement incident p intensité débouchant à la perte de fourche est égal à ( α / 2 ν ) ⋅ p ² /2. La puissance du flux entrant dans la fourche racine est: n , par conséquent, l'intensité des pertes dans le nœud racine est: ( α / 2 ν ) ⋅ n ²/ 2. Dans chaque génération suivante de l'arborescence d'adresses, le nombre de fourches double et la puissance du flux qui les exécute est divisée par deux. Par conséquent, la formule de perte à l'intérieur de l'arbre entier prendra la forme:

I _{t_div1} = ( α / 2 ν ) ⋅ (1/2) ⋅ [ n ² + 2 ( n / 2) ² + 4 ( n / 4) ² + ... + ( n / 2) ⋅ 2 ² ] =

( α / 2 ν ) ⋅ ( n / 2) ² [1 + 1/2 + 1/4 + ... + 2 /n ] ≈ ( α / 2 ν ) ⋅ n ²

Étant donné que la puissance du flux de déplacement généré conjointement par tous les points d'adresse est n , les coûts de temps par trajet sont en moyenne ( α / 2 ν ) ⋅ n , montrant ainsi un linéaire dépendance à la taille de la ville.

En ce qui concerne les réseaux abstraits, il est difficile de donner une estimation significative de la superficie des routes qu'ils utilisent. Comme mesure alternative de la complexité structurelle, la puissance totale de tous les flux latéraux peut être calculée. Comme prévu, la valeur résultante devrait refléter le coût en ressources de l'érection de tous les échangeurs requis par le réseau. Je ne peux pas dire que dans la pratique, cette méthode aura toujours une bonne interprétation, mais je serai probablement en mesure d'avoir une idée approximative de la quantité de travail à venir.

À l'intérieur du réseau logarithmique avec fusion préliminaire, les flux latéraux ne sont présents que dans l'arborescence d'adresses directe, et leur puissance totale pour chaque génération de nœuds est la même: n / 2. Journal de l'arbre total ₂ ngénérations de nœuds, donc une nouvelle façon d'évaluer la complexité donne une estimation de la complexité: O ( n log ₂ n ).

Réseau logarithmique avec fusion préliminaire
Nombre de points d'adresse de la puissance de l'unité ........................................ ............ n
Temps de trajet moyen
perdu à cause des coûts de changement:
comportement asymptotique ........................ .................................................. ............................ O ( n )
valeur exacte ................ .................................................. ........................... ( α / 2 ν ) ⋅ n
Le nombre de nœuds de commutation ............................................... .................................. O ( n )
Le nombre de nœuds de commutation en tenant compte de la puissance des flux latéraux .... ............... O ( n log ₂ n )

Pertes dans le réseau avec séparation préliminaire
Passons maintenant à l'analyse du réseau logarithmique avec séparation préliminaire, en supposant à nouveau que le réseau est utilisé pour connecter des points d'adresse de l'alimentation de l'unité dans la ville de «l'accès uniforme».

La figure 16 en montre un fragment, composé d'un point d'adresse et d'arbres d'adresses directs et inverses adjacents à ce point.


fig. 16

Tout d'abord, nous estimons l'intensité des pertes de commutation générées par le fragment.
Les coûts encourus pour diviser les flux peuvent être trouvés en substituant dans la formule I _{t_div1} = ( α / 2 ν ) ⋅ n ² , dérivée pour l'arbre d'adresse directe dans l'exemple précédent, au lieu de n - un. En effet, les arbres d'adresse directe des figures 16 et 14 ont la même profondeur et conduisent des flux d'épaisseur similaire ( _{env.la similitude signifie la possibilité d'obtenir un ensemble de valeurs en multipliant les valeurs d'un autre ensemble par un certain nombre fixe, pour illustrer, la similitude entre les triangles de leurs côtés peut être utilisée} ). En raison de la dépendance quadratique entre la valeur des coûts de commutation résultant d'une fourche séparée et la puissance du flux qui lui est fourni, une diminution simultanée de tous les flux de n fois réduira les pertes dans l'arbre entier de n ² fois, donc au lieu de l'ancien ( α / 2 ν ) ⋅ n ² nous on obtient une valeur égale à:

I _{t_div2} = ( α / 2 ν ).

Nous calculons maintenant la valeur des coûts dans la moitié gauche du fragment.
En raison de l'étroitesse des débits combinés de la route à l'intérieur de l'arbre d'adresse inversé, cette fois, il ne serait pas raisonnable de construire plus de deux voies. Les fusions dans ces conditions ne coûtent plus rien: contrairement à l'exemple précédent, il y a des points de rétrécissement sur l'autoroute (Fig. 17), où des coûts de changement seront nécessaires.


fig. 17

En supposant que le conducteur est au courant du rétrécissement à venir, nous pouvons supposer que le processus de déplacement des voitures de la voie sans issue est lent, s'étendant sur des centaines de mètres le long de l'autoroute. Dans ce cas, nous avons le droit de recourir à l'astuce que nous avons utilisée plus tôt pour calculer les pertes à la fourche symétrique - pour diviser le flux de migration total q en plusieurs petites parties q _i , puis interpréter chacune d'elles comme un flux latéral du côté de la rampe. Les pertes générées par chacun de ces sous-flux sont calculées par la formule:
I _i = ( α / 2 ν ) ⋅ p q _i ⋅ (1 + 1 / s), cependant, il existe deux subtilités.

Le premier est que les voitures ne migreront pas plus loin que la rangée suivante.
Et en fait: les flux dans les deux voies centrales, en raison d'une symétrie évidente, devraient toujours avoir approximativement la même densité, de sorte que les conducteurs n'auront pas beaucoup de raisons de traverser la ligne médiane. De l'observation faite, il s'ensuit que dans la formule pour les pertes causées par le flux latéral partiel, s est égal à 1.

Au fur et à mesure que les machines quittent les voies extrêmes, se réorganisant en deux rangées centrales, la puissance de flux à l'intérieur des bandes centrales augmente progressivement, changeant dans chaque cas de P / 2 à P . Ainsi, la deuxième subtilité est une dépendance significative de pà partir du numéro du sous-flux i , ce qui nous oblige à écrire non:

I _i = ( α / 2 ν ) ⋅ p q _i ⋅ (1 + 1 / s ),
mais:
I _i = ( α / 2 ν ) p ( i ) ⋅ q _i ⋅ (1 + 1 / s ).
Dans le cas où de nombreuses petites parties dans lesquelles le flux migratoire a été divisé étaient toutes de taille égale, la dépendance p ( i ) est exprimée par un graphique linéaire (Fig.18)


fig. 18

Pour calculer l'intensité des pertes totales, il faut soit recourir à l'intégration, soit (cela permet de faire une forme particulièrement simple d'une fonction intégrable) car p ( i ) prendre la valeur moyenne sur le graphique égale à 3 P / 4. Étant donné que le flux de migration total du côté de chaque bande extrême est P / 2, l'intensité des pertes lors d'une fusion distincte sera:

je _fusionne = 2 ⋅ ( α / 2 ν ) ⋅ (3 P / 4) ⋅ ( P / 2)

= ( α / 2 ν ) 3 P ²/ 4.

Pour trouver les pertes de temps générées à l'intérieur du fragment sur l'arbre d'adresse inverse, nous appliquons la formule pour I _fusionner à chacun de ses _nœuds :

I _{t_merge} = (3/4) ⋅ ( α / 2 ν ) [1 ⋅ (1/2) ² + 2 ⋅ (1/4) ² + 4 ⋅ (1/8) ² + ... + ( n / 2) ⋅ (1 / n ) ² ] ≈

≈ (3/4) ⋅ ( α / 2 ν ) [1/4 + 1/8 + 1/16 + ...] =

= (3/8)⋅ ( α / 2 ν ) [1/2 + 1/4 + 1/8 + ...] =

= (3/8) ⋅ ( α / 2 ν ).

Les coûts totaux engagés dans le fragment en raison de la fusion et de la séparation des flux seront:

I _{t_merge} + I _{t_div2} = ( α / 2 ν ) [1 + 3/8] = 11/8 ( α / 2 ν ).

Un réseau logarithmique fractionné préliminaire ne contient que n de tels fragments, et exactement nles flux unitaires sont générés par ses points d'adresse, par conséquent, la valeur que nous venons de trouver est juste égale aux pertes de commutation qui se produisent en moyenne par trajet.

En fait, il est plus important pour nous, même pas un nombre spécifique, qui est égal aux coûts de commutation spécifiques, mais le fait que ces coûts restent constants avec l'augmentation de n . Cette dernière circonstance fait que le réseau logarithmique avec séparation préliminaire est asymptotiquement le plus économique en termes de pertes de commutation, parmi tous les types de réseaux que nous avons étudiés précédemment.

Malheureusement, le leadership ne coûte pas «gratuitement». Malgré la taille extrêmement faible du nombre écrasant de flux, chaque arbre d'adresses inclus dans le réseau contient environ 2 nnervures de route à deux voies et environ n nœuds de commutation de taille normale. Il y a 2 n arbres dans le réseau , ce qui signifie O ( n ² ) arêtes et nœuds, ce qui le rend non seulement le plus économique dans le temps, mais aussi le réseau le plus cher à construire, parmi tous les exemples considérés.

Quant à la somme des flux latéraux, sa valeur, facile à calculer, croît avec la vitesse O ( n log2 n ) et dans ce cas n'a pas beaucoup de sens.

Réseau logarithmique avec séparation préliminaire
Nombre de points d'adresse de la puissance de l'unité ........................................ ............ n
Durée moyenne du trajet,
perdu en raison des coûts de commutation:
asymptotique .......................................... .................................................. .......... O (1)
valeur exacte .................................. .................................................. ........... 11/8 ( α / 2 ν ).
Le nombre de nœuds de commutation ............................................... .................................. O ( n ² )
Le nombre de nœuds de commutation en tenant compte de la puissance des flux latéraux ... ................ O ( n log ₂ n )

Réseau logarithmique équilibré

Des pertes de commutation exceptionnellement faibles, avec l'utilisation possible d'un réseau logarithmique avec séparation préliminaire, mais en même temps trop gourmande en ressources de sa construction, provoquent le désir de trouver un moyen de modifier sa conception afin que la consommation de ressources soit considérablement réduite et que les coûts de commutation n'augmentent pas de manière significative.

De toute évidence, le principal coupable d'un nombre excessivement élevé de routes du réseau est la très faible efficacité de leur utilisation. Ce dernier est clairement visible sur la figure 19, qui montre un diagramme détaillé des flux à l'intérieur d'une arborescence d'adresses directe adjacente au i- ème point d'adresse.


fig. 19

Dans le diagramme, le nombre situé au-dessus du bord de l'arbre indique la puissance du flux de déplacement passant le long du bord, et l'intervalle ci-dessous est l'ensemble des points d'adresse entre lesquels ce flux sera éventuellement distribué. On pense que tous les bords présents sur le diagramme sont des autoroutes à deux voies, le nombre de bords dans chaque génération de l'arbre est indiqué au bas de la figure.

En y regardant de plus près, vous remarquerez peut-être que la règle selon laquelle le flux de déplacement est divisé en un nœud particulier est déterminée uniquement par la position de ce nœud dans l'arborescence d'adresses et ne dépend pas du numéro du point d'adresse qui a donné lieu à ces déplacements.

S'il y a plusieurs flux adressés au même ensemble de points, et que chacun d'eux n'est pas assez puissant pour remplir son chemin alloué, alors pourquoi ne pas les combiner ensemble sur une même route. En fait, cette idée essentiellement simple permet de construire un bon réseau abstrait, générant des pertes de commutation relativement faibles, et économique en nombre de routes utilisées.

En revenant à l'arborescence d'adresses du i- ème point, nous voyons que le flux entrant dans le nœud racine est divisé en deux flux enfants d'une capacité de 1/2 chacun. Le premier flux beau-fils se compose de trajets adressés à des points de l'intervalle [1; n / 2], le second - voyages adressés aux points de l'intervalle [( n / 2) + 1;n ].
Suivant l'idée décrite ci-dessus, nous combinons le même type de flux beau-fils à chaque point impair et au point d'adresse suivant avec un nombre pair qui le suit dans l'ordre. Une telle technique permet à chaque paire de points sélectionnée d'avoir au lieu de quatre flux avec une puissance de 1/2 seulement deux flux de grandeur unitaire (Fig. 20). Nous donnerons l'abréviation BN ₂ [i; i +1].


fig. 20

Si les flux du beau-fils n'étaient pas combinés, mais étaient toujours à l'intérieur de l'arborescence d'adresses, alors dans la prochaine génération de nœuds atteints, chacun d'entre eux serait à nouveau divisé en deux parties, égales en puissance et en taille des ensembles de ces points auxquels composantes de leurs voyages.

Pourquoi briser la tradition établie, car après l'unification, nous avons toujours le même ensemble de types de flux qu'auparavant, mais avec seulement moins de représentants de chaque type? - applicable à chacun des flux de sortie BN ₂ [i; i +1] exactement la même règle de séparation qui s'appliquerait à un flux de son type à l'intérieur de l'arborescence d'adresses.

Il n'y a aucune raison pour que la construction logique décrite ci-dessus pour combiner-diviser les mêmes flux ne puisse pas être répétée de manière inductive. La figure 21 montre un diagramme de combinaison de deux fragments de
BN ₂ en un fragment de BN ₄ , et la figure 22 montre à quoi ressemble l'algorithme dans le cas général.


fig. 21


fig. 22

Au final, le processus d'agrandissement de la fragmentation sera achevé et nous conduira au seul élément BN _n [1; n ], nous l'appellerons le réseau équilibré de type logarithmique (Fig. 23).


fig. 23

Examinons ce réseau pour la complexité et l'ampleur des pertes de commutation générées.
En fonction de la nature inductive de la procédure de construction du réseau équilibré, le nombre de nœuds de commutation inclus dans sa structure peut être décrit par l'équation de retour:

nœuds (BN _k ) = 2 nœuds (BN _{k / 2} ) + 2 k ,

avec la condition aux limites:

nœuds (BN ₁ ) = 0. La

solution à ce système d'équations est la fonction:

nœuds (BN _n ) = 2 n log ₂ n .

Depuis pour construire BN _nSi log ₂ n étapes d'induction sont nécessaires , alors chaque trajet passera par les nœuds de séparation log ₂ n et le même nombre de nœuds de fusion, en les alternant sur son chemin (Fig. 24).


fig. 24

Les pertes générées dans chaque ensemble de séparation:
( α / 2 ν ) ⋅ (1) ² /2.

Les pertes générées dans chaque noeud de fusion:
( α / 2 ν ) ⋅ 3 ⋅ (1/2) ² /4 = 3/16 ( α / 2 ν ).

En considérant que les deux dans le réseau équilibré sont n log ₂ n , nous obtenons la valeur exacte des pertes de commutation totales:
11/16 ( α / 2 ν ) n log ₂ n ,

qui par trajet est:
11/16 ( α / 2 ν ) log ₂ n

Réseau équilibré de type logarithmique
Nombre de points d'adresse de la puissance de l'unité ................... ................................. n
Temps de trajet moyen
perdu à cause des coûts de changement:
comportement asymptotique ... .................................................. ................................................. O (log ₂ n )
valeur exacte ........................................... .................................................. Journal ..11 / 16 ( α / 2 ν )₂ n
Nombre de nœuds de commutation ............................................. .................................... O ( n log ₂ n )
Le nombre de nœuds de commutation, en tenant compte de la puissance du côté threads ................... O ( n log ₂ n )

Les chiffres ci-dessus permettent au réseau équilibré d'être considéré comme un bon compromis entre la quantité de perte de temps introduite et la complexité structurelle globale. Son utilisation comme réseau routier d'une ville réelle est en principe possible, mais difficilement économiquement réalisable. Il me semble que le domaine dans lequel l'utilisation du réseau équilibré peut réellement être très utile est celui des systèmes d'information à grande échelle avec des exigences strictes en matière de retard du signal, telles que les communications cellulaires, Internet, l'informatique distribuée, les ordinateurs multiprocesseurs. Pour nous, la valeur principale du Réseau équilibré est la méthode par laquelle il a été construit. Un peu plus tard, en utilisant une modification de cette méthode, nous pourrons améliorer les réseaux de centres linéaires et cellulaires qui sont vraiment importants sur le plan pratique.

Pourquoi les villes historiques sont condamnées aux embouteillages

Ma déclaration peut sembler inattendue, mais la réponse à la raison pour laquelle les villes en développement naturel, souffrent généralement d'embouteillages, a déjà été trouvée par nous dans les paragraphes précédents. En quoi cela consiste-t-il?

Le fait est que de nombreuses villes historiques qui ont survécu à l'époque des forteresses médiévales (par exemple, presque toutes les capitales du «Vieux Monde») ont hérité de cette époque de la structure radiale des rues. Malheureusement (pour leurs habitants modernes), un réseau routier de topologie similaire n'est pas très évolutif: la localisation dense des routes radiales à proximité du centre devient trop rare en périphérie. En conséquence, dans le processus de croissance démographique, les rues qui étaient initialement situées en marge des quelques routes menant à la forteresse sont devenues plus grandes et les rues qui sont apparues à la périphérie étaient courtes et n'ont pas acquis une importance de transport suffisante pour croître en largeur. En conséquence, le réseau routier que nous voyons maintenant dans les grandes villes historiques se réfère maintenant le plus souvent à des systèmes de transport de type artériel,et dans notre terminologie, au type de réseaux logarithmiques avec fusion préliminaire (incomplète).


(Routes de Moscou, photo: Stepanov Slava)

Si nous parlons de la longueur du chemin qu'un conducteur doit parcourir le long des routes, la mise en œuvre de ce type de réseau n'est pas mauvaise: la distance parcourue diffère souvent peu de la distance en ligne droite, et sa valeur moyenne dans la ville, comme il devrait l'être pour les systèmes de transport «décents», il croît à une vitesse de O (√ n ). Tout le problème est qu'avec l'élargissement de la ville au réseau logarithmique avec une fusion préliminaire, les coûts de commutation générés par celui-ci augmentent trop rapidement: la durée pendant laquelle le voyage est prolongé en moyenne en raison d'eux dépend du nombre de personnes vivant dans la ville comme O ( n ) Il est clair qu'à partir de certains n, ce temps l'emportera sur le temps pur pour surmonter la distance, en d'autres termes, des embouteillages apparaîtront dans la ville.

Il ne fait aucun doute que la réorganisation du système de transport dans les grandes villes historiques est une tâche qui peut être résolue. Cependant, il est important de comprendre ici que la construction d'une autre, deux ou cinq grandes artères de transport améliore certes légèrement la situation dans la ville, mais la cause profonde des embouteillages ne sera pas éliminée. Apparemment, la seule façon de surmonter les lacunes du réseau logarithmique avec une fusion préliminaire est d'utiliser un autre réseau. Un bon candidat ici peut être un réseau avec des topologies cellulaires, pour lequel le taux de croissance du temps pour couvrir la distance, au moins, coïncide avec le taux de croissance des pertes de commutation.


(nuit Berlin, photo: Vincent Laforet)

C'est peut-être pour cela que le Berlin moderne, bien qu'il ait de grandes autoroutes artérielles, se distingue déjà par une structure en mailles clairement visible.

Il existe de nombreuses solutions intéressantes dans le monde pour rendre les habitants des villes historiques plus mobiles, mais le prix principal de la lutte pour l'accessibilité des transports devrait probablement être remis aux ingénieurs de Barcelone.


(Réseau routier modernisé de Barcelone, photo: Vincent Laforet)

Un aperçu détaillé des réseaux de villes linéaires et cellulaires

Après avoir trouvé et affiné les méthodes d'analyse sur des réseaux abstraits, il était temps de les appliquer à des cas plus réalistes de villes à topologie linéaire et cellulaire. Dans cette section, nous essaierons d'analyser en détail les caractéristiques de leurs liaisons de transport, d'établir la valeur numérique de l'intensité de la perte de commutation, de trouver comment sa valeur dépend de la taille des quartiers et de discuter des variations et améliorations possibles.

Ville linéaire
Cette fois, considérons un exemple de ville dans laquelle il y a deux rues à sens unique: l'ouest avec un mouvement vers le nord et l'est avec un mouvement vers le sud (figure 25).


fig. 25

Laissez chaque trimestre générer un flux de déplacement de la puissance unitaire. Dans ce cas, un itinéraire menant d'un bloc à un autre représente 1 / n flux de trafic .

Nous définissons pour commencer la puissance des flux latéraux sur les autoroutes. La
rue Zapadnaya est le seul moyen de se rendre au bloc i à partir de
( n - i ) quartiers se trouvant au sud, et le seul moyen de se rendre du quartier i à ( i - 1) quartiers au nord . Il s'ensuit que la capacité des flux d'échange de trafic entre la rue Zapadnaya et le i- ème trimestre est égale à:

q _{W_out} = ( n - i ) / n - pour le flux latéral quittant West Street,
q _{W_in} = ( i - 1) / n - pour le flux latéral adjacent au trafic sur celui-ci. Il est clair que la puissance des flux latéraux sur la rue Vostochnaya dépend de i symétriquement:
q _{E_out} = ( i - 1) / n est la puissance de celui qui part,
q _{E_in} = ( n - i ) / n est la puissance du flux latéral adjacent au trafic sur la rue Vostochnaya .

Bien sûr, la somme des flux sortant du ième trimestre:

q _{E_in} + q _{W_in} = ( n - 1) / n ,
coïncide avec la somme des flux qui y entrent:
q _{E_out} + q _{E_out} = ( n - 1) / n ,
et les deux les valeurs ne dépendent en aucune façon de i (chaque trimestre a un flux de déplacement de magnitude 1 / n , qui commencent et se terminent à l'intérieur de lui-même).

Pour trouver la puissance des principaux flux, tracez une ligne imaginaire à travers la Western Highway au même niveau que i-th trimestre. Au total, cette ligne sera franchie par:
(le nombre de trimestres d'en bas) × (le nombre de trimestres d'en haut) = ( n - i ) ( i - 1) des itinéraires créant ensemble un flux de grandeur:

P _W ( i ) = ( n - i ) ( i - 1 ) / n .

La même formule:
(nombre de trimestres d'en bas) × (nombre de trimestres d'en haut) / n , la
puissance P _E du flux de circulation sur la rue Vostochnaya doit être exprimée , en d'autres termes:

P _E ( i ) = P _W( i ) = P ( i ).

Connaissant la puissance de tous les flux principaux et secondaires, nous pouvons calculer l'intensité des pertes qui se produisent dans le réseau dans la zone proche du i- ème trimestre:

I ( i ) = ( α / 2 ν ) ⋅ P ( i ) ⋅ [( q _{E_in} + q _{W_in} ) ⋅ (1 + 1 / s ) + ( q _{E_out} + q _{E_out} ) ⋅ (1 - 1 / s )] =
= ( α / 2 ν ) ⋅ P ( i ) ⋅ [(1 - 1 / n ) ⋅ (1 + 1 / s ) + (1 - 1 / n ) ⋅ (1 - 1 / s )] =
= ( α / 2 ν ) ⋅ 2 P ( i ) ⋅ (1 - 1 / n ) =
= 2 ( α / 2 ν ) ⋅ (1 - 1 / n ) ⋅ ( n - i) ( i - 1) / n =
= 2 ( α / 2 ν ) ⋅ (1 - 1 / n ) ⋅ ( n - i ) ⋅ ( i - 1) ⋅ (1 / n ).

Si nous additionnons la dernière expression sur i , alors nous obtenons l'intensité des pertes générées par l'ensemble du réseau dans son ensemble.

I = ∑ _i I ( i )
= ∑ _i 2 ( α / 2 ν ) ⋅ (1 - 1 /n ) ⋅ ( n - i ) ⋅ ( i - 1) ⋅ (1 / n ) =
= 2 ( α / 2 ν ) ⋅ (1 - 1 / n ) ⋅ n ² ⋅ ∑ _i (1 - i / n ) ⋅ ( i / n - 1 / n ) ⋅ (1 / n ) ≈
≈ 2 ( α / 2 ν ) ⋅ n ² ⋅ ∑ _i ( i / n ) ⋅ (1 - i / n ) ⋅ (1 / n ).

La somme ∑ _i ( i / n ) ⋅ (1 - i / n ) ⋅ (1 / n ) pour tout grand n peut être remplacée avec une bonne précision par l'intégrale:

∫ t (1 - t ) d t ( t ∈ [0; 1]) = 1/2 - 1/3 = 1/6.

Ce qui implique que l'intensité des pertes de commutation à la distance linéaire de n blocs de capacité unitaire de:

I = ( α / 2 ν ) n ² /3.

Jusqu'à ce moment, nous n'avons considéré que des exemples dans lesquels les trimestres généraient toujours des flux de puissance unitaire. Voyons si la formule des pertes de commutation de la ville linéaire change s'il n'y a pas une seule source de puissance unitaire pour chaque trimestre, mais - λ (les trimestres deviendront λ fois plus grands).

Prenez une ville avec m blocs. Si les trimestres ont généré des flux de puissance 1, alors les pertes de commutation seraient ( α/ 2 ν ) m ² /3. Augmenter chaque Voyage quart de la production d'énergie à X fois conduit à une augmentation de λ et le principal et le côté cours d' eau en même temps, de sorte que le coût à chaque jonction, et des moyens au sein du réseau dans son ensemble augmente dans X ² fois, et la perte de formule prend la forme:

I = ( α / 2 ν ) m ² ⋅ X ² /3.

Dans l'ensemble, peu importe comment les pertes de commutation dépendent du nombre de quartiers dans la ville, l'essentiel pour nous est de savoir comment elles dépendent du flux de puissance de tous les déplacements générés à l'intérieur, ou en d'autres termes, du nombre n de sources d'énergie unitaires. Dans ce cas , n est égal à m ⋅ X , donc:

I = ( α / 2 ν ) m ² ⋅ X ² /3 =
= ( α / 2 ν ) ( m ⋅ X ) ² /3 =
= ( α / 2 ν) N ^deux / 3.

En d'autres termes, les pertes de commutation dans la ville linéaire ne dépendent pas de la petitesse de sa division en quartiers.

Cellular City
Imaginez une ville cellulaire dans laquelle les autoroutes perpendiculaires les unes aux autres sont espacées à différentes hauteurs. Cela est possible, par exemple, si toutes les routes menant du nord au sud sont surélevées sur des ponts et que des routes s'étendant d'ouest en est sont construites à la surface de la terre. Si, en outre, toutes les rues ont un trafic à double sens, la feuille de route dans une telle ville sera référée à la topologie cellulaire standard (Fig. 26).

Il ne s'agit bien sûr pas de mettre sérieusement en pratique le réseau décrit ci-dessus: il ne serait pas trop esthétique sur le fond du paysage urbain et, en outre, en raison de la nécessité d'échanges à plusieurs niveaux, il consommerait une bonne moitié de l'espace de la rue. Néanmoins, ce réseau purement hypothétique est un bon moyen d'obtenir les estimations nécessaires, qui pourront ensuite être facilement étendues à des réseaux routiers vraiment intéressants du point de vue de leur applicabilité dans les villes réelles.

Comme d'habitude, nous supposerons que les besoins migratoires des résidents sont décrits par le modèle «d'accès uniforme», et nous commencerons notre examen par le cas où la capacité de tous les flux de déplacement générés par un trimestre distinct est de 1.

Dans l'exemple de la ville cellulaire standard, il est commode de s'éloigner de la tradition établie et de considérer le point d'adresse non pas comme un quartier séparé, mais comme une zone territoriale de forme carrée, qui capture l'intersection des autoroutes et du quart de tous les quartiers adjacents. La figure 27 montre le positionnement relatif de plusieurs de ces zones et montre un modèle de trafic à l'intérieur de l'une d'entre elles. Ce diagramme montre clairement que tout conducteur, quittant le quartier, a la possibilité de monter sur l'autoroute, en direction de l'une des quatre parties du monde.


fig. 26

Pour trouver la valeur des coûts de commutation générés par la ville, nous calculons la puissance de tous les flux principaux et secondaires au sein de chacune de ses zones territoriales. La forme et l'agencement mutuel des zones nous permettent de recourir à une analogie aux échecs pour résoudre le dernier problème, en considérant les zones comme des cellules du champ et le mouvement des voitures entre elles - les mouvements du bateau (Fig.27). D'une cellule à l'autre, à condition qu'elles soient en «position générale» l'une par rapport à l'autre, la tour peut être déplacée en deux mouvements, et si les deux cellules se trouvent sur la même horizontale ou une même verticale, puis en une seule.


fig. 27

Afin d'éviter de nombreuses réservations gênantes, nous supposons que le mouvement dans lequel la tour ne se déplace nulle part est également autorisé selon nos règles. L'itinéraire de déplacement de la tour, composé de deux mouvements, dont l'un est nécessairement exécuté verticalement et l'autre horizontalement, est appelé le plus simple. Il est raisonnable de considérer le déplacement «en place» à la fois vertical et horizontal en même temps. Dans ce cas, l'affirmation est vraie que deux cellules de la carte sont connectées l'une à l'autre par exactement deux routes les plus simples différentes.

Pour les conducteurs, l'itinéraire «le plus simple» est le moyen le plus simple de se déplacer avec une interférence minimale d'une zone territoriale à une autre, il est donc raisonnable de supposer que de vrais trajets auront lieu le long des lignes de route élémentaires. Selon le modèle d '«accès uniforme» généré par le point d'adresse (zone territoriale), le flux de puissance unitaire devrait être réparti également entre tous les n = d ² points d'adresse de la ville, ainsi la capacité du flux de circulation se déplaçant le long d'une ligne de route est de 1 / (2 n ).

Nous calculons le flux de quelle grandeur passe à travers la cellule ( i , j ) dans la direction du sud au nord. L'itinéraire le plus simple traverse la cellule (i , j ) du sud au nord dans seulement deux situations. Le premier d'entre eux (Fig.28 à gauche):

1a) la cellule initiale de l'itinéraire est située dans l'une des dernières ( d - i ) courbes de niveau (lignes);
2a) le point final de l'itinéraire est l'une des premières ( i - 1) cellules de la jième verticale (colonne);
3a) itinéraire commence par la section horizontale, ou se trouve entièrement à l'intérieur de la j -ième colonne.


fig. 28

Les conditions décrivant la deuxième situation semblent symétriques (Fig. 28 à droite):

1b) le point de départ de l'itinéraire est l'une des dernières ( d - i ) cellules de la jième verticale;
2b) de la route finale , la cellule est dans l' un des premier ( i - 1) contour
3b) itinéraire commence par la partie verticale ou se trouve entièrement à l'intérieur de la j la colonne.

Il n'y a que 2 × [ d ⋅ ( i - 1) + 1 ⋅ ( i - 1)] × ( d - i sur le terrain d'échecs) adapté aux exigences des routes les plus simples, qui créent ensemble un flux de capacité:

P _SN ( i , j ) = ( d + 1) ⋅ ( i - 1) ⋅ ( d - i ) / n (= P _SN ( i )).

En fixant j , on obtient la fonction

( P _SN ) _j ( i ) = P _SN ( i , j = Const),

décrivant la dépendance du flux de puissance, au nord de j autoroute verticale, la distance de la ville de bordure supérieure mesurée dans les cellules.
Il y a plusieurs observations plus ou moins évidentes concernant les fonctions ( P _SN ) _j ( i ), discutons-en.

Nous commençons peut-être par une circonstance qui serait difficile à ignorer: P _SN ( i , j ) est en fait indépendant du deuxième argument. En conséquence, les fonctions ( P _SN ) _j ( i ) = P _SN ( i) ont la même forme pour toutes les valeurs de j , en d'autres termes, la position spécifique de la rue à l'intérieur de la ville cellulaire n'affecte en rien sa charge. Formellement, la dernière déclaration n'est prouvée que pour l'autoroute menant au nord, mais en raison des symétries de la ville, elle s'étend automatiquement à l'autoroute d'autres directions également.

Examinons maintenant la formule elle-même pour P _SN ( i ):

( d + 1) ⋅ ( i - 1) ⋅ ( d - i ) / (2 n ).

Comme nous le voyons, toute la dépendance de P _SN sur iréside dans l'expression ( i - 1) ⋅ ( d - i ). Cette expression peut être interprétée comme le produit des longueurs des intervalles droit et gauche dans lesquels le segment entier de longueur d se divise après que le i- ème élément en soit éliminé (Fig. 29a).


fig. 29a


fig. 29b

Il est clair que si vous changez «droite» en «gauche» et «gauche» en «droite» (Fig. 29b), le résultat du travail restera le même. À partir d'une observation aussi simple, il y a essentiellement deux conclusions qui nous sont très utiles:

1. P _SN ( i ) i = ( d + 1)/2, , Δ , Δ .
2. - , ( P _NS ) _j ( i ), j - , , - ( P _SN ) _j ( i ) i = ( d + 1)/2. ( P _SN ) _j ( i ) = P _SN ( i ), P _SN ( i ) i = ( d + 1)/2 , ( P _NS ) _j ( i ) = P _SN ( i ) = P _vert ( i ), , . P _SN ( i ) 30 (, d >> 1, i >> 1, d − i >> 1).

fig. 30

Les puissances des principaux flux le long des routes horizontales sont facilement trouvées en utilisant des symétries de rotation; formellement, ce processus se résume à un simple remplacement de i par j dans P _SN ( i ) et une petite version de l'indice inférieur.

La prochaine chose à faire est de trouver la puissance des flux latéraux. Les déplacements qui entrent ou sortent de la circulation sur une autoroute verticale à l'intérieur de la cellule ( i , j ) peuvent être commodément divisés en quatre catégories:

1. écoulement q _{in_transit} : initiale - une cellule i -ième horizontal fini - une cellule j -ième verticalement, à l' exception de la ( i , j ) (figure 31a);
2. q _{out_transit} : — j - , ( i , j ), — i - ( 31b);
3. q _in : — ( i , j ), — i - ( 31c);
4. q _out : — i - . — ( i , j ) ( 31d).

fig. 32: abcd Après avoir

raconté le nombre de lignes de route appartenant à chaque catégorie distincte, nous concluons que les puissances des quatre flux sont identiques et égales:

q ₀ = d ⋅ ( d - 1) / (2 n )

Avoir les valeurs des puissances des flux principal et latéral sur une autoroute verticale, il n'est pas difficile de calculer le montant des coûts engendrés par leur commutation. A l'intérieur d'une seule cellule ( i , j ), les coûts seront égaux à:

I _vert ( i , j ) = ( α / 2 ν ) ⋅ P _vert( i ) ⋅ [( q _in + q _{in_transit} ) ⋅ (1 + 1 / s ) + ( q _out + q _{out_transit} ) ⋅ (1 - 1 / s )]
= 4 ( α / 2 ν ) ⋅ ( d + 1) ( i - 1) ( d - i ) ⋅ d ( d - 1) / 2 n ² ≈
≈ 2 ( α / 2 ν) ⋅ d ⁵ ⋅ ( i / d ) (1 - i / d ) ⋅ (1 / d ) ⁴ =
= 2 ( α / 2 ν ) ⋅ d ² ⋅ ( i / d ) (1 - i / d ) ⋅ (1 / j ).

Pour trouver les coûts encourus sur les rues verticales dans toute la ville, nous devons additionner I _vert ( i , j) pour les deux indices:

I _vert = ∑ _ij I _vert ( i , j ) =
2 ( α / 2 ν ) ⋅ d ² ⋅ ∑ _ij ( i / d ) (1 - i / d ) ⋅ (1 / d ) .

Étant donné que l'ampleur des termes ne dépend en aucune façon de j , la sommation sur le deuxième indice équivaut à la multiplication par d :

∑ _ij ( i / d) (1 - i / d ) ⋅ (1 / d ) = d ⋅ ∑ _i ( i / d ) (1 - i / d ) ⋅ (1 / d ).

La dernière somme peut être approximée par l'intégrale qui nous est déjà familière:

∑ _i ( i / d ) (1 - i / d ) ⋅ (1 / d ) ≈ ∫ t (1 - t ) d t ( t∈ [0; 1]) = 1/2 - 1/3 = 1/6. Ce

qui implique que

I _vert = ( α / 2 v ) ⋅ d ³ /3 = ( α / 2 v ) ⋅ n √ n / 3.

À la question de savoir quelle est la valeur des coûts I _horiz résultant des autoroutes horizontales, en utilisant la symétrie de la ville, la réponse est:

I _horiz = I _vert = ( α / 2 ν ) ⋅ n √ n / 3.

Ainsi, l'intensité des pertes de commutation au sein de l'ensemble du réseau de la ville cellulaire standard est:

I = I _vert + I _horiz = 2/3 ⋅ ( α / 2 ν ) ⋅ n √ n ,

et le coût moyen par trajet est de

2/3 ⋅ ( α / 2 ν ) ⋅ √ n

Effet de la taille des cellules sur la valeur des pertes de commutation
Les trimestres générant des flux de puissance unitaire constituent une limitation plutôt artificielle des conditions du problème. Nous étendons les résultats obtenus ci-dessus aux cas où la puissance du flux de déplacement généré par une cellule territoriale est égale à λ .
Soit la ville composée de m de telles cellules. Si toutes les cellules n'avaient qu'une puissance unitaire, alors l'intensité des pertes de commutation totales serait I ₁ = 2/3 ⋅ ( α / 2 ν ) ⋅ m √ m . Une augmentation du nombre de voyages effectués par λ fois en λles temps augmenteront la puissance de tous les flux principaux et latéraux des autoroutes, ce qui entraînera à son tour une augmentation de λ ² de tous les coûts de commutation générés dans la ville. La nouvelle formule de l'intensité des pertes prendra donc la forme:

I = 2/3 ⋅ ( α / 2 ν ) λ ² ⋅ m √ m

Si nous supposons que la cellule est constituée de λ adresses de points de puissance unitaire, alors le nombre total de ces points sera: n = λ m . Exprimons I en fonction de n et λ :

I= 2/3 ⋅ ( α / 2 ν ) λ ² ⋅ m √ m =
= 2/3 ⋅ ( α / 2 ν ) ⋅ √ λ ⋅ ( λ √ λ ) ⋅ ( m √ m )
= 2/3 ⋅ √ λ ( α / 2 ν ) ⋅ ( λ m ) √ ( λ m )
= 2/3 ⋅√ λ ( α / 2 ν ) ⋅ n √ n .

Le coût moyen par trajet dans les nouvelles conditions sera de 2/3 ⋅ √ λ ( α / 2 ν ) ⋅ √ n , soit √ λ fois supérieur à leur valeur dans une ville composée d'unités de capacité unitaire.

La dernière formule nous dit que pour la même population, densité de population et superficie totale de toutes les routes, le coût des coûts de commutation est plus élevé, plus les quartiers au moment de la conception de la ville ont été choisis par son architecte. Dans le cas où la population de la ville est inégalement répartie sur son territoire, il ne faut bien sûr pas prêter attention aux dimensions géométriques, mais principalement au nombre moyen de personnes à l'intérieur du quartier et à leur activité migratoire.


(Photo du centre-ville de New York: Vincent Laforet)

La remarque ci-dessus est particulièrement importante lors de la conception de zones avec des bâtiments de gratte-ciel. En raison de la combinaison d'une densité de population élevée et de sa grande mobilité, il est souhaitable de faire des quartiers dans des zones de haute altitude plusieurs fois plus petites que ce qui est habituel pour la construction d'étages standard. Dans les civilisations, où la construction de gratte-ciel a une longue histoire, la pratique d'isoler même de grands bâtiments séparés comme un bloc est répandue.

Feux de circulation Cellular City
Dans chaque cas, lorsque les lignes de deux routes très fréquentées se croisent sur la carte, l'architecte doit faire un choix: soit soulever l'une de ces routes jusqu'au pont, permettant à l'écoulement de l'autre de passer librement par le bas, soit réaliser l'intersection sous la forme d'une intersection régulière, et résoudre le conflit de flux entraînant un trafic réglementation. La deuxième option attire par sa simplicité, l'absence de la nécessité de construire des structures d'ingénierie à grande échelle, et en plus, elle fournit un moyen facile de traverser la route pour les piétons, pour ces raisons dans les villes, ils la préfèrent souvent.


(après-midi du centre-ville de Los Angeles, photo: Boris Shein)

L'utilisation des feux de circulation dans les réseaux à topologie cellulaire a ses propres caractéristiques. Dans le chapitre 1, il a été montré qu'avec une bonne synchronisation des feux de circulation, les voitures, lorsqu'elles circulent dans la même rue, n'ont même pas à s'arrêter aux intersections: le feu vert s'allume toujours dans leur direction. Ce type de phénomène est généralement appelé le régime des vagues vertes . Pour le créer, les flux de trafic doivent être divisés en deux zones alternées de deux types: remplies de voitures et libres de celles-ci. Ensuite, un tel mode de fonctionnement des feux de circulation est sélectionné pour que pendant la période où la prochaine «portion» passe l'intersection le long d'une des rues, la portion précédente des voitures se déplaçant le long de la rue perpendiculaire l'a déjà dépassée et la suivante n'est pas encore arrivée (Fig. 33).


fig. 33

La capacité de conduire du trafic en mode vert entraîne ses propres coûts et impose certaines restrictions sur la disposition des rues de la ville.

Si l'on regarde de nouveau la figure 33, il est facile de voir qu'à un moment donné exactement la moitié de la superficie de toutes les routes n'est pas réellement utilisée. Afin de compenser la simplicité, sur la moitié de la chaussée utilisée, la puissance locale des flux automobiles et le nombre de voies nécessaires doivent être deux fois plus importants que dans une ville avec des viaducs.

La deuxième circonstance la plus importante associée à l'utilisation des vagues vertes est la réglementation stricte de la taille autorisée des quartiers: leur longueur (pour les rues à double sens) doit être un multiple de la longueur de la vague verte remplie (une section du ruisseau à l'intérieur de laquelle un mouvement sans entrave est possible), soit environ 500 mètres. Comme indiqué au paragraphe précédent, les zones à forte densité de population nécessitent une fréquence accrue de localisation des routes, de sorte que la restriction par le bas de la distance entre les autoroutes peut potentiellement entraîner des problèmes de circulation.

Il est intéressant de noter que dans le mode des vagues vertes, les règles changent légèrement en fonction des itinéraires de voyage qui sont commutés à l'intérieur du réseau. Par exemple, la connexion d'une autre voiture au flux de circulation principal sur une route de rue peut être effectuée entre les zones remplies, n'entraînant ainsi pas de coûts de commutation graves (point «1» sur la figure 34a).


fig. 34

Bien sûr, cette voiture elle-même devra perdre un peu de temps à attendre la zone vide la plus proche avant de monter sur l'autoroute, et après cela, restez au feu jusqu'à ce que la prochaine zone pleine l'atteigne (point «2», Fig. 34a), cependant l'ampleur de ces pertes ne dépend ni de la taille de la ville, ni de la fréquentation de la circulation dans la rue, de sorte qu'elles peuvent être négligées à grande échelle.

La situation est complètement différente si une voiture essaie de laisser la circulation sur une autoroute (Fig. 34b). Ici, selon toute vraisemblance, il n'y a déjà aucun moyen difficile de réduire les pertes de commutation créées par lui. De plus, en raison du doublement de la puissance locale du débit à l'intérieur des zones remplies, la suppression d'une voiture choisie arbitrairement en coûte deux fois plus cher que dans une ville avec des viaducs. Au total, le coût réduit de «l'entrée» et la «sortie» plus chère des flux de la rue se compensent mutuellement, ce qui rend le Traffic Light Cell City à cet égard pas encore meilleur, mais pas pire que Standard.

Ville cellulaire à sens unique
En plus de l'utilisation des feux de circulation, il y a au moins une autre opportunité de s'éloigner des échangeurs monstrueux de la ville standard. Elle consiste à diviser spatialement (Fig. 35) les routes à sens de déplacement opposé.


fig. 35

À la suite de ces changements, le nombre de rues doublera, elles deviendront toutes à sens unique, mais surtout, les échangeurs seront grandement simplifiés (Fig. 36).


fig. 36
Étant donné que le nombre d'autoroutes menant à chacune des Parties au monde et le nombre de trajets les traversant sont restés les mêmes, les capacités de tous les flux et, avec eux, les coûts de commutation dans la ville cellulaire à sens unique et la ville standard avec deux grands quartiers (linéaires) devraient correspondre. Si nous comparons les villes standard et unilatérales avec les mêmes tailles de quartier, la seconde aura deux fois les pertes de commutation.

Rue "linéaire".

Comment réduire les pertes de commutation dans un réseau cellulaire? La réponse à cette question nous permettra de sélectionner avec succès l'analogie et un peu de bon sens.

Considérons une modification quelque peu inhabituelle du réseau cellulaire, ce qui implique que toutes les autoroutes qui s'étendent d'ouest en est sont à double sens, tandis que sur les routes perpendiculaires à celles-ci, la circulation n'est autorisée que dans une seule direction: au nord ou au sud, et ces directions alternent de rue en rue.

Comme toujours, nous supposerons que la ville obéit au modèle d'accès uniforme et que chaque quart de celui-ci génère un flux de déplacements de puissance unitaire conditionnelle.

Dans ce cas, il semble plausible que le noyau à l'intérieur du quartier ( i , j) le flux de déplacements, en le quittant, est réparti entre les rues les plus proches comme suit: 1/4 de celui-ci arrive à la route horizontale par le haut, 1/4 de plus à la route horizontale par le bas, 1/4 ⋅ i / d s'écoule vers le nord le long de la route verticale et
1/4 ⋅ (1 - i / d ) - le long de la deuxième autoroute verticale au sud (Fig.37).

fig. 37

En effet, selon les algorithmes de construction d'itinéraire précédemment discutés, selon les statistiques, la moitié des trajets commencera à partir d'une section horizontale, et pour les conducteurs qui préfèrent cette moitié, cela devrait avoir peu importe si leur chemin se situe au nord du quartier ( i , j ) ou au sud de lui. La moitié restante des trajets débutera par une section verticale de la circulation et sera divisée entre les autoroutes sud et nord en fonction du nombre de quartiers situés ( i , j ) au sud et du nombre de quartiers situés au nord.

Quant au flux de voyage dirigé vers l'intérieur ( i , j), alors la règle de sa division par rapport à l'autoroute entourant le quartier sera symétrique (Fig.38).


fig. 38

Parmi les quatre intersections adjacentes au quartier ( i , j ), nous considérons séparément les flux latéraux à l'intersection de la route horizontale inférieure et de la rue verticale avec circulation vers le nord (Fig.38). Machine à flux entrant dans une position horizontale pour un aperçu vertical est la suivante :
1/2 ⋅ (le nombre de blocs dans le plan horizontal) x (le nombre de blocs en vertical pas au- dessous ( i , j )) ⋅ 1 / d ² =
= 2.1 ⋅ d ⋅ i / d ² =
= 1/2 ⋅ i / d .
L'ampleur de l'écoulement latéral dans la direction opposée est la suivante :
1/2 ⋅ (le nombre de blocs verticaux strictement inférieure à ( i , j )) x (le nombre de blocs en vertical) ⋅ 1 / d ² =
= 2.1 ⋅ ( d - i ) ⋅ d / d ² =
= 1/2 ⋅ (1 - i / d ).

Tournons maintenant notre attention de la ville cellulaire dans son ensemble vers l'une de ses rues verticales, appelons-la My_street. En raison de symétries, nous ne limiterons pas du tout notre raisonnement, si nous supposons que le mouvement le long de My_street est dirigé du sud au nord (Fig. 39).


fig. 39

La figure 40 représente les graphiques de la puissance des flux principaux et latéraux sur l'autoroute le long de My_street, qui, comme le lecteur le remarquera peut-être, sont incroyablement similaires à des graphiques similaires pour l'autoroute à sens unique de Linear City (figure 26).



fig. 40

Dans ces exemples, les diagrammes de flux coïncident complètement si à l'intérieur de My_street les flux latéraux liés à chaque paire de quartiers opposés et la route horizontale en dessous d'eux sont officiellement affectés à une cellule territoriale imaginaire. Comme le montrent les tableaux précédents, le réseau routier de la ville linéaire génère certaines des pertes de commutation les plus importantes parmi les réseaux des architectures que nous avons déjà étudiés. De ce point de vue, le modèle de circulation dans une rue de ville à cellule unique semble extrêmement inefficace et est un élément qui devrait être essayé d'améliorer en premier lieu.

Réseau avancé pour Linear City
Et donc, nous sommes confrontés à la tâche d'améliorer le réseau linéaire afin qu'il ne se transforme pas en réseau "carré". La circonstance qui introduit la plus grande inefficacité dans le fonctionnement du réseau linéaire est son unification de toutes les routes en seulement deux flux de trafic très importants. Dans cette situation, une étape raisonnable consisterait à diviser les débits le long de ses deux autoroutes en Q parties égales. Étant donné que les coûts de temps causés par chaque voiture entrant ou sortant du trafic sont proportionnels à l'intensité du trafic sur celle-ci, en raison de la division des lignes de rue en Q parties isolées (Fig.41a), les pertes de commutation à l'intérieur de la ville linéaire auraient dû diminuer d'un facteur Q.


fig. 41

Il suffit de construire dix routes à proximité et d'espérer que les conducteurs eux-mêmes soient également répartis entre eux - malheureusement, il ne semble pas y avoir de chance de succès. Une décision beaucoup plus réfléchie est de concevoir le réseau de sorte que chaque route ne mène pas à tous les quartiers, mais seulement à un petit «segment» de la ville, où il serait difficile de la contourner (Fig. 41b).

Vous pouvez voir une idée similaire dans le schéma de mouvement des ascenseurs à l'intérieur des bâtiments à plusieurs étages. Là, chaque ascenseur vous permet d'entrer et de sortir non pas à tous les étages, mais uniquement dans une certaine plage de hauteurs. Reprenant ce concept, regardons de plus près la route r _k , qui ouvre l'accès au segment Δ _k = ( x _k ,x _{k +1} ] pour les déplacements qui ont commencé (non strictement) au sud de x _k (on pense que la numérotation des blocs se fait de bas en haut). Du côté de chaque trimestre, dont le nombre (strictement) inférieure à x _{les k} , la route r _k entre le flux q _en puissance | Δ _k | / n (1 / n chaque adresse de chaque quartier à l'intérieur de Δ _k ), en même temps, on suppose que la capacité de s'effondrer avec r _kvers l'un des quartiers mentionnés est manquant soit en raison des règles de circulation établies, soit en raison de la conception spéciale du réseau routier.

Accumulée sur l'intervalle [1, x _k ] voitures ont finalement été également réparties entre les quartiers du delta _{du k} , donc si vous ne voyageraient pas là, le début et la fin qui se trouvent dans le delta _{du k} , l'écoulement latéral q _hors dans la direction de chacun des blocs dans ce domaine aurait une puissance x _k / n (Fig. 42).


fig. 42

En fait, la contribution des voyages «internes» à la puissance des flux latéraux a également lieu, cependant, la valeur de cette contribution ne dépasse jamais | Δ _k | / n , donc dans le cas où x _k >> | Δ _k |, il peut être simplement négligé. La puissance p _{k du} flux principal le long de r _k avec les simplifications apportées sera représentée par un graphique de deux sections droites avec un maximum P _k égal à x _k ⋅ | Δ _k | / n . La valeur approximative des pertes de commutation à r _k peut être trouvée par la formule:

I _k = ( α / 2 ν ) ⋅ ∑ _x [ q _in ( x ) ⋅ p _k ( x ) ⋅ (1 + 1 / s )] + ( α / 2 ν ) ⋅ ∑ _x [ q _out ( x ) ⋅ p _k ( x ) ⋅ (1 - 1 / s )] =

= ( α / 2 ν ) ⋅ (1 + 1 / s ) ∑ _x [| Δ _k | / n ⋅ p _k ( x )] + ( α / 2 ν ) ⋅ (1 - 1 / s ) ∑ _x [ x _k / n ⋅ p _k ( x )] =

= ( α / 2 ν ) ⋅ (1 + 1 / s ) ⋅ ( x _k ⋅ | Δ _k | / n ) ⋅ ( ∑ _x p _k ( x )) / x _k + ( α / 2 ν ) ⋅ (1 - 1 / s ) ⋅ ( x _k ⋅ | Δ _k | / n ) ⋅ ( ∑ _x p _k ( x )) / | Δ _k |,

où la première somme est prise sur l'aire x ∈ [1, x _k ], et la seconde sur x ∈ Δ _k . Expressions:

( ∑ _x p _k ( x )) / x _k , x ∈ [1, x _k ] et

( ∑ _x p _k ( x )) / | Δ _k |, x ∈ Δ _k

il n'y a rien de plus que la puissance moyenne du flux le long de r _k à l'intérieur des intervalles indiqués. Étant donné que le graphique de puissance dans ces intervalles a la forme d'une ligne droite, la puissance moyenne dans les deux cas est P _k / 2. Remplacement
x _k ⋅ | Δ _k | / n sur
P _k
nous donnons enfin la formule de l'intensité de la perte à sa forme la plus simple:

I _k = 2 ( α / 2 ν ) ⋅ P _k ⋅ P _k / 2 = ( α / 2 ν ) ⋅ P _k ²

Essayons maintenant de calculer la séquence x _{k des} nombres de ces quartiers par lesquels la ville linéaire doit être divisée en segments. Comme critère de sélection des segments, nous prenons l'exigence que la puissance maximale des flux de trafic P _k sur des routes adaptées ait la même valeur, indépendamment de k , en d'autres termes, l'égalité

x _k ⋅ | Δ _k | = Const.

Se souvenir de cela | Δ _k | = x _{k + 1} - x _k , on arrive à l'équation de différence:

x _{k + 1} - x _k = Const / x _k .

En supposant que x et k sont des variables continues et en remplaçant

x _{k + 1} - x _k = x ( k + 1) - x ( k )

sur d x / d k ⋅ 1,

on peut approximer l'équation de différence par différentiel:

d x / d k = Const / x <=> x d x = Const ⋅ d k .

D'où on obtient pour x _{k une} solution sous la forme générale:

x _k = C ₁ √ ( k + C ₂ ).

Il nous reste à déterminer la valeur des constantes C ₁ et C _{2 à} partir des conditions aux limites, cependant, il y a une subtilité importante dans cette matière. Contrairement à la situation dans les segments restants, toutes les voitures arrivant de l'autoroute ouest aux quartiers du segment au numéro 1, à l'intérieur du même segment, ont commencé leur voyage. En conséquence, le graphique de la puissance d'écoulement sur la première autoroute au nord aura la forme d'une parabole inversée régulière.

En même temps, les conditions a priori à partir desquelles la formule de x _{k a} été obtenue suggéraient essentiellement que les graphiques de puissance d'écoulement sur toutes les autoroutes devraient être proches d'une vue triangulaire, et que les voyages eux-mêmes devraient commencer principalement en dehors du segment où ils sont dirigés. Ces exigences peuvent être satisfaites avec une précision raisonnable si nous divisons formellement le premier segment en deux parties égales (la parabole est approchée par un triangle isocèle et la plupart des trajets le long de la première autoroute sont en effet dirigés de la moitié sud du segment numéro 1 à sa moitié nord), sans augmenter le nombre de routes ( fig 43).


fig. 43

C'est le milieu du premier segment qui doit être considéré comme le point x ₁ dans la formule de x _k . De là, nous obtenons la première condition aux limites:

x ₂ = 2 x ₁ ou

√ (2 + C ₂ ) = 2 ⋅ √ (1 + C ₂ ) =>

C ₂ = - 2/3.

La deuxième condition aux limites est obtenue à partir de l'exigence que les routes et les segments soient exactement Q , ce qui signifie que x _{Q + 1} doit être égal au trimestre suivant avec le plus grand nombre dans la ville:

C ₁ √ ( Q + 1 - 2/3) = n + 1, d'où

C ₁ ≈ ( n + 1) / √ Q.

De cette façon:

x _k ≈ ( n + 1) ⋅ √ ( k - 2/3) / √ Q ,

| Δ _k | ≈ d x / d k = ( n + 1) / 2√ ( k - 2/3) ⋅ √ Q

P _k = x _k ⋅ | Δ _k | / n =

= ( n + 1) 2/2 n ⋅ Q ≈ n / 2 Q

I _k = ( α / 2 ν ) ⋅ P _k ² =

= ( α / 2 ν ) ⋅ ( n / 2 Q ) ² .

Étant donné que toutes les autoroutes 2 Q génèrent des pertes de même intensité, la valeur des coûts de commutation dans l'ensemble du réseau dans son ensemble sera:

I = 2 Q ⋅ ( α / 2 ν ) ⋅ ( n / 2 Q ) ² = ( α / 2 ν ) ⋅ n 2/2 Q.

Comme vous pouvez le voir, le résultat souhaité est atteint: après la division des autoroutes principales en parties Q , les pertes ont vraiment diminué d'un facteur Q (à l'exception du coefficient constant 1/3 à 1/2 qui a augmenté par rapport à la formule de la ville linéaire habituelle). Eh bien, la moitié du travail est fait, il reste à appliquer le résultat pour améliorer la ville avec l'architecture cellulaire.

Ascenseur de gratte-ciel dans la ville cellulaire
Par souci de simplicité, nous nous contenterons d'un exemple de ville dans laquelle toutes les rues sont à sens unique. En utilisant l'analogie entre la ville linéaire et les rues individuelles de la ville cellulaire, nous divisons l'autoroute le long de cette dernière en parties Q. Par défaut, on pense qu'en quittant le quartier, vous pouvez emprunter n'importe quelle autoroute qui passe à proximité. En même temps, parmi toutes les autoroutes tracées le long d'une rue, il y a un virage vers un quartier spécifique avec exactement l'une d'entre elles. Dans le processus d'établissement des règles, leur uniformité et leur simplicité sont extrêmement importantes. Jetez un oeil à la figure 44:


fig. 44

toutes les rues ont la même apparence et les mêmes règles, lesquelles de leurs routes dans quels blocs de compte ouvrent l'accès. La figure 45 montre un diagramme des virages autorisés entre les autoroutes. En regardant cette photo, il est difficile de ne pas se confondre. La même chose est souvent dite à propos du réseau de métro dans certaines grandes villes. Cependant, dans les deux cas, tout devient clair et simple si vous connaissez la logique de l'idée. La règle logique des virages autorisés semble assez simple: si vous conduisez le long d'une autoroute, vous traversez des routes perpendiculaires à votre mouvement et vous pouvez vous transformer en un quartier situé directement derrière eux, vous pouvez tourner sur l'une de ces routes.


fig. 45

La topologie du Skyscraper Lift est compatible avec les feux de circulation et les viaducs. Il est difficile, mais peut être généralisé à des réseaux pas nécessairement de structure cellulaire ou linéaire. Ce dernier est vraiment important pour les villes historiques, où il est peu probable qu'il soit juste de démolir la moitié des monuments historiques afin de créer de nombreuses petites rues droites, mais dans lesquelles il existe déjà de très grandes rues pouvant accueillir plusieurs autoroutes à deux ou trois voies.

A propos des problèmes de transport et du travail des mathématiques

Il est agréable de terminer le travail minutieux semestriel. Le travail que j'ai écrit, bien sûr, ne résout pas tous les problèmes et difficultés de la conception des routes - cette entreprise nécessite un grand nombre de personnes très diverses. Néanmoins, ses résultats fournissent une occasion de voir des erreurs importantes dans des villes déjà construites et fournissent des méthodes pour éviter de telles erreurs à l'avenir. Cet article n'a pas été conçu comme un ouvrage de référence couvrant tous les cas possibles qu'un ingénieur peut rencontrer dans la pratique - j'ai considéré que ma tâche principale était de donner un nouveau point de vue, de développer une nouvelle façon de raisonner et de parler du problème, de fournir le minimum nécessaire d'exemples de modèles simples préparés par le lecteur. pourrait déjà me développer.

Cela devient triste quand vous réalisez combien de temps a été perdu par les habitants de la ville dans les embouteillages simplement parce qu'au bon moment, aucun mathématicien ne pouvait passer la soirée sur un problème complètement résoluble. Combien de ces problèmes entourent encore notre vie ou se cachent dans votre profession? Est-ce qu'une personne assise près de chez vous au travail dont les outils ont un crayon et une feuille de papier?

J'espère que tout change pour le mieux.

Merci pour votre attention et bonne chance!
Sergey Kovalenko.

2019 année
magnolia@bk.ru


(Photo: Vincent Laforet)