Approche gourmande et machines à sous. Analyse des tâches de la piste ML du championnat de programmation

Nous continuons à publier des analyses des tâches qui ont été proposées lors du récent championnat. Viennent ensuite les tâches issues du cycle de qualification pour les spécialistes de l'apprentissage automatique. Il s'agit de la troisième piste sur quatre (backend, frontend, ML, analytics). Les participants devaient créer un modèle pour corriger les fautes de frappe dans les textes, proposer une stratégie pour jouer sur les machines à sous, évoquer un système de recommandations de contenu et composer plusieurs autres programmes.

A. Typos

Condition

(épigraphe) (d'un forum)
- Qui a composé ce non-sens?
- Astrophysiciens. Ce sont aussi des gens.
- Vous avez fait 10 erreurs dans le mot «journalistes».

De nombreux utilisateurs font des fautes de frappe, certaines à cause de la frappe des touches et d'autres à cause de leur analphabétisme. Nous voulons vérifier si l'utilisateur pourrait réellement avoir à l'esprit un autre mot que celui qu'il a tapé.

Plus formellement, supposons que le modèle d'erreur suivant se produise: l'utilisateur commence par un mot qu'il veut écrire, puis y fait ensuite un certain nombre d'erreurs. Chaque erreur est une substitution d'une sous-chaîne du mot pour une autre sous-chaîne. Une erreur correspond au remplacement d'une seule position (c'est-à-dire que si l'utilisateur veut faire une seule erreur par la règle "abc" → "cba", alors à partir de la chaîne "abcabc" il peut obtenir soit "cbaabc" ou "abccba"). Après chaque erreur, le processus se répète. La même règle peut être utilisée plusieurs fois à différentes étapes (par exemple, dans l'exemple ci-dessus, «cbacba» peut être obtenu en deux étapes).

Il est nécessaire de déterminer le nombre minimum d'erreurs qu'un utilisateur pourrait commettre s'il avait en tête un mot donné et en écrivait un autre.

Solution

Essayons de générer à partir de l'orthographe correcte tous les mots possibles avec pas plus de 4 erreurs. Dans le pire des cas, il peut y avoir O ((L﹒N) ⁴ ). Dans les limites du problème, il s'agit d'un nombre assez important, vous devez donc comprendre comment réduire la complexité. Au lieu de cela, vous pouvez utiliser l'algorithme de rencontre au milieu: générer des mots avec pas plus de 2 erreurs, ainsi que des mots à partir desquels vous pouvez obtenir un mot écrit par l'utilisateur avec pas plus de 2 erreurs. Notez que la taille de chacun de ces ensembles ne dépassera pas 10 ⁶ . Si le nombre d'erreurs commises par l'utilisateur ne dépasse pas 4, ces ensembles se recouperont. De même, nous pouvons vérifier que le nombre d'erreurs ne dépasse pas 3, 2 et 1.

 struct FromTo { std::string from; std::string to; }; std::pair<size_t, std::string> applyRule(const std::string& word, const FromTo &fromTo, int pos) { while(true) { int from = word.find(fromTo.from, pos); if (from == std::string::npos) { return {std::string::npos, {}}; } int to = from + fromTo.from.size(); auto cpy = word; for (int i = from; i < to; i++) { cpy[i] = fromTo.to[i - from]; } return {from, std::move(cpy)}; } } void inverseRules(std::vector<FromTo> &rules) { for (auto& rule: rules) { std::swap(rule.from, rule.to); } } int solve(std::string& wordOrig, std::string& wordMissprinted, std::vector<FromTo>& replaces) { std::unordered_map<std::string, int> mapping; std::unordered_map<int, std::string> mappingInverse; mapping.emplace(wordOrig, 0); mappingInverse.emplace(0, wordOrig); mapping.emplace(wordMissprinted, 1); mappingInverse.emplace(1, wordMissprinted); std::unordered_map<int, std::unordered_set<int>> edges; auto buildGraph = [&edges, &mapping, &mappingInverse](int startId, const std::vector<FromTo>& replaces, bool dir) { std::unordered_set<int> mappingLayer0; mappingLayer0 = {startId}; for (int i = 0; i < 2; i++) { std::unordered_set<int> mappingLayer1; for (const auto& v: mappingLayer0) { auto& word = mappingInverse.at(v); for (auto& fromTo: replaces) { size_t from = 0; while (true) { auto [tmp, wordCpy] = applyRule(word, fromTo, from); if (tmp == std::string::npos) { break; } from = tmp + 1; { int w = mapping.size(); mapping.emplace(wordCpy, w); w = mapping.at(wordCpy); mappingInverse.emplace(w, std::move(wordCpy)); if (dir) { edges[v].emplace(w); } else { edges[w].emplace(v); } mappingLayer1.emplace(w); } } } } mappingLayer0 = std::move(mappingLayer1); } }; buildGraph(0, replaces, true); inverseRules(replaces); buildGraph(1, replaces, false); { std::queue<std::pair<int, int>> q; q.emplace(0, 0); std::vector<bool> mask(mapping.size(), false); int level{0}; while (q.size()) { auto [w, level] = q.front(); q.pop(); if (mask[w]) { continue; } mask[w] = true; if (mappingInverse.at(w) == wordMissprinted) { return level; } for (auto& v: edges[w]) { q.emplace(v, level + 1); } } } return -1; } 

Bandit armé de plusieurs armes

Condition

Il s'agit d'une tâche interactive.

Vous ne savez pas comment cela s'est passé, mais vous vous êtes retrouvé dans une salle avec des machines à sous avec un sac entier de jetons. Malheureusement, au box-office, ils refusent d'accepter les jetons et vous avez décidé de tenter votre chance. Il y a beaucoup de machines à sous dans la salle que vous pouvez jouer. Pour un jeu avec une machine à sous, vous utilisez un jeton. En cas de victoire, la machine vous donne un dollar, en cas de perte - rien. Chaque machine a une probabilité fixe de gagner (que vous ne connaissez pas), mais elle est différente pour différentes machines. Après avoir étudié le site Web du fabricant de ces machines, vous avez découvert que la probabilité de gagner pour chaque machine est sélectionnée au hasard au stade de la fabrication à partir de la distribution bêta avec certains paramètres.

Vous souhaitez maximiser vos gains attendus.

Solution

Ce problème est bien connu, il pourrait être résolu de différentes manières. La décision principale du jury a mis en œuvre la stratégie d' échantillonnage de Thompson , mais comme le nombre d'étapes était connu au début du programme, il existe des stratégies plus optimales (par exemple, UCB1). De plus, on pourrait même s'en sortir avec la stratégie epsilon-greedy: avec une certaine probabilité ε jouer une machine aléatoire et avec une probabilité (1 - ε) jouer une machine avec les meilleures statistiques de victoire.

 class SolverFromStdIn(object): def __init__(self): self.regrets = [0.] self.total_win = [0.] self.moves = [] class ThompsonSampling(SolverFromStdIn): def __init__(self, bandits_total, init_a=1, init_b=1): """ init_a (int): initial value of a in Beta(a, b). init_b (int): initial value of b in Beta(a, b). """ SolverFromStdIn.__init__(self) self.n = bandits_total self.alpha = init_a self.beta = init_b self._as = [init_a] * self.n # [random.betavariate(self.alpha, self.beta) for _ in range(self.n)] self._bs = [init_b] * self.n # [random.betavariate(self.alpha, self.beta) for _ in range(self.n)] self.last_move = -1 random.seed(int(time.time())) def move(self): samples = [random.betavariate(self._as[x], self._bs[x]) for x in range(self.n)] self.last_move = max(range(self.n), key=lambda x: samples[x]) self.moves.append(self.last_move) return self.last_move def set_reward(self, reward): i = self.last_move r = reward self._as[i] += r self._bs[i] += (1 - r) return i, r while True: n, m = map(int, sys.stdin.readline().split()) if n == 0 and m == 0: break alpha, beta = map(float, sys.stdin.readline().split()) solver = ThompsonSampling(m) for _ in range(n): print >> sys.stdout, solver.move() + 1 sys.stdout.flush() reward = int(sys.stdin.readline()) solver.set_reward(reward) 

C. Alignement des peines

Condition

L'une des tâches les plus importantes pour former un bon modèle de traduction automatique est un bon cas de phrases parallèles. En règle générale, la source des offres parallèles est constituée de documents parallèles. Il s'avère que souvent pour construire un certain corpus de phrases parallèles, il n'est pas nécessaire de connaître autre chose que leur longueur. En particulier, vous remarquerez peut-être que plus la phrase est longue dans la langue source, plus elle sera traduite longtemps. Une certaine difficulté réside dans le fait que pendant la traduction, le nombre de phrases dans le texte peut changer: parfois deux phrases adjacentes dans la traduction peuvent être combinées en une seule, ou vice versa - une phrase peut être divisée en deux. Dans certains cas rares, des phrases peuvent être entièrement omises dans une traduction, ou une traduction peut apparaître dans une traduction qui n'était pas dans l'original.

Plus formellement, supposons que le modèle génératif suivant pour les enceintes parallèles soit vrai. À chaque étape, nous effectuons l'une des opérations suivantes:

1. Arrêtez

Avec la probabilité p _{h, la} génération des coques se termine.

2. [1-0] Ignorer les offres

Avec la probabilité p _{d, nous} attribuons une phrase au texte original. Nous n'attribuons rien à la traduction. La longueur de la phrase dans la langue d'origine L ≥ 1 est choisie dans la distribution discrète:

.

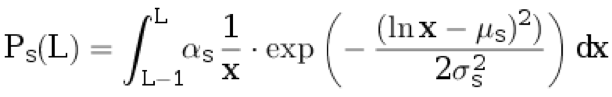
Ici μ _s , σ _s sont les paramètres de distribution, et α _s est le coefficient de normalisation choisi pour que .

3. [0-1] Insérer une proposition

Avec la probabilité p _{i nous} attribuons une phrase à la traduction. Nous n'attribuons rien à l'original. La longueur d'une phrase dans une langue de traduction L ≥ 1 est choisie dans une distribution discrète:

.

Ici μ _t , σ _t sont les paramètres de distribution, et α _t est le coefficient de normalisation choisi pour que .

4. Traduction

Avec la probabilité (1 - p _d - p _i - p _h ) on prend la longueur de la phrase dans la langue d'origine L _s ≥ 1 de la distribution p _s (avec arrondi). Ensuite, nous générons la longueur de la phrase dans la langue de traduction L _t ≥ 1 à partir de la distribution discrète conditionnelle:

.

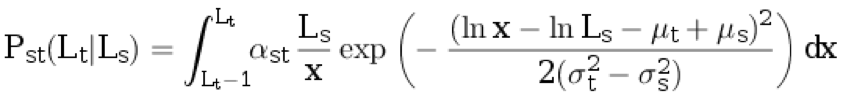
Ici, α _st est le coefficient de normalisation, et les paramètres restants sont décrits dans les paragraphes précédents.

La prochaine étape est une autre:

1. [2-1] Avec la probabilité p _{divisé s, la} phrase générée dans la langue d'origine se divise en deux phrases non vides, de sorte que le nombre total de mots augmente exactement d'un . La probabilité qu'une phrase de longueur L _{s se} décompose en parties de longueur L ₁ et L ₂ (c'est-à-dire L ₁ + L ₂ = L _s + 1) est proportionnelle à P _s (L ₁ ) ⋅ P _s (L ₂ ).

2. [1-2] Avec la probabilité p _{divisée t, la} phrase générée dans la langue cible se divise en deux phrases non vides, de sorte que le nombre total de mots augmente d'exactement une. La probabilité qu'une phrase de longueur L _{t se} désagrège en parties de longueur L1 et L2 (c'est-à-dire L ₁ + L ₂ = L _t + 1) est proportionnelle à P _t (L ₁ ) ⋅ P _t (L ₂ ).

3. 3. [1-1] Avec une probabilité de (1 - p _{split s} - p _{split t} ), aucune des deux phrases générées ne se désintègre.

Solution

La tâche est un cas particulier d'alignement utilisant des modèles de Markov cachés (alignement HMM). L'idée principale est que vous pouvez calculer la probabilité de générer une paire spécifique de documents en utilisant ce modèle et l'algorithme de transfert : dans ce cas, l'état est une paire de préfixes de document. Par conséquent, la probabilité requise d'alignement d'une paire spécifique de phrases parallèles peut être calculée par l'algorithme avant-arrière .

D. Bande de recommandations

Condition

Considérez un flux de recommandations pour le contenu hétérogène. Il mélange des objets de différents types (photos, vidéos, actualités, etc.). Ces objets sont généralement classés par pertinence pour l'utilisateur: plus l'objet est pertinent (intéressant) pour l'utilisateur, plus il se trouve en haut de la liste des recommandations. Cependant, avec un tel classement, des situations surviennent souvent dans lesquelles plusieurs objets du même type apparaissent dans la liste des recommandations. Cela aggrave considérablement la variété externe de nos recommandations et les utilisateurs n'aiment donc pas. Il est nécessaire de mettre en œuvre un algorithme qui, selon la liste des recommandations, constituera une nouvelle liste qui sera exempte de ce problème et sera la plus pertinente.

Soit une liste initiale de recommandations donnée a = [a ₀ , a ₁ , ..., a _{n - 1} ] de longueur n> 0. Un objet avec le nombre i a le type avec le nombre b _i ∈ {0, ..., m - 1}. De plus, un objet sous le numéro i a une pertinence r (a _i ) = 2 _−i . Considérons la liste obtenue à partir de l'initial en choisissant un sous-ensemble d'objets et en les réarrangeant: x = [a _{i 0} , a _{i 1} , ..., a _{i k - 1} ] de longueur k (0 ≤ k ≤ n). Une liste est dite admissible si deux objets consécutifs ne coïncident pas en type, c'est-à-dire b _{i j} ≠ b _{i j + 1} pour tout j = 0, ..., k - 2. La pertinence de la liste est calculée par la formule $$$\ sum_ {j = 0} ^ {k-1} 2 _ {- j} r (a_ {i_j})$. Vous devez trouver la liste de pertinence maximale parmi toutes les valides.

Solution

À l'aide de calculs mathématiques simples, on peut montrer que le problème peut être résolu par une approche «gourmande», c'est-à-dire que dans la liste optimale de recommandations, chaque élément a l'objet le plus pertinent de tous qui sont valides au même début de la liste. La mise en œuvre de cette approche est simple: nous prenons des objets dans une rangée et les ajoutons à la réponse, si possible. Lorsqu'un objet invalide est rencontré (dont le type coïncide avec le type du précédent), nous le mettons de côté dans une file d'attente séparée, à partir de laquelle nous l'insérons dans la réponse dès que possible. Notez qu'à chaque instant, tous les objets de cette file d'attente auront un type correspondant. À la fin, plusieurs objets peuvent rester dans la file d'attente, ils ne seront plus inclus dans la réponse.

  std::vector<int> blend(int n, int m, const std::vector<int>& types) { std::vector<int> result; std::queue<int> repeated; for (int i = 0; i < n; ++i) { if (result.empty() || types[result.back()] != types[i]) { result.push_back(i); if (!repeated.empty() && types[repeated.front()] != types[result.back()]) { result.push_back(repeated.front()); repeated.pop(); } } else { repeated.push(i); } } return result; } 

D. Clusterisation des séquences de caractères

Il y a un alphabet fini A = {a ₁ , a ₂ , ..., a _{K - 1} , a _K = S}, a _i ∈ {a, b, ..., z}, S est la fin de la ligne.

Considérez la méthode suivante pour générer des chaînes aléatoires sur l'alphabet A:

1. Le premier caractère x ₁ est une variable aléatoire de distribution P (x ₁ = a _i ) = q _i (on sait que q _K = 0).
2. Chaque caractère suivant est généré sur la base du précédent conformément à la distribution conditionnelle P (x _i = a _j || x _{i - 1} = a _l ) = p _jl .
3. Si x _i = S, la génération s'arrête et le résultat est x ₁ x ₂ ... x _{i - 1} .

L'ensemble des lignes générées à partir d'un mélange de deux modèles décrits avec des paramètres différents est donné. Il est nécessaire que chaque ligne donne l'index de la chaîne à partir de laquelle elle a été générée.

Solution

Le problème est résolu en utilisant l' algorithme EM : on suppose que l'échantillon présenté est généré à partir d'un mélange de deux chaînes de Markov dont les paramètres sont restaurés au cours des itérations. Une restriction de 80% des bonnes réponses est faite afin que l'exactitude de la solution ne soit pas affectée par les exemples qui ont une forte probabilité dans les deux chaînes. Par conséquent, lorsqu'ils sont correctement restaurés, ces exemples peuvent être affectés à une chaîne incorrecte en termes de réponse générée.

 import random import math EPS = 1e-9 def empty_row(size): return [0] * size def empty_matrix(rows, cols): return [empty_row(cols) for _ in range(rows)] def normalized_row(row): row_sum = sum(row) + EPS return [x / row_sum for x in row] def normalized_matrix(mtx): return [normalized_row(r) for r in mtx] def restore_params(alphabet, string_samples): n_tokens = len(alphabet) n_samples = len(string_samples) samples = [tuple([alphabet.index(token) for token in s] + [n_tokens - 1, n_tokens - 1]) for s in string_samples] probs = [random.random() for _ in range(n_samples)] for _ in range(200): old_probs = [x for x in probs] # probs fixed p0, A = empty_row(n_tokens), empty_matrix(n_tokens, n_tokens) q0, B = empty_row(n_tokens), empty_matrix(n_tokens, n_tokens) for prob, sample in zip(probs, samples): p0[sample[0]] += prob q0[sample[0]] += 1 - prob for t1, t2 in zip(sample[:-1], sample[1:]): A[t1][t2] += prob B[t1][t2] += 1 - prob A, p0 = normalized_matrix(A), normalized_row(p0) B, q0 = normalized_matrix(B), normalized_row(q0) trans_log_diff = [ [math.log(b + EPS) - math.log(a + EPS) for b, a in zip(B_r, A_r)] for B_r, A_r in zip(B, A) ] # A, p0, B, q0 fixed probs = empty_row(n_samples) for i, sample in enumerate(samples): value = math.log(q0[sample[0]] + EPS) - math.log(p0[sample[0]] + EPS) for t1, t2 in zip(sample[:-1], sample[1:]): value += trans_log_diff[t1][t2] probs[i] = 1.0 / (1.0 + math.exp(value)) if max(abs(x - y) for x, y in zip(probs, old_probs)) < 1e-9: break return [int(x > 0.5) for x in probs] def main(): N, K = list(map(int, input().split())) string_samples = [] alphabet = list(input().strip()) + [''] for _ in range(N): string_samples.append(input().rstrip()) result = restore_params(alphabet, string_samples) for r in result: print(r) if __name__ == '__main__': main() 

---

.