Une explication accessible de l'algorithme d'effondrement de la fonction d'onde

L'algorithme d'effondrement de la fonction d'onde enseigne à un ordinateur à improviser. En entrée, il reçoit des données archétypales et crée des données générées de manière similaire à l'original.


( Source )

Le plus souvent, il est utilisé pour créer des images, mais il peut également construire des villes , des skateparks et écrire de terribles poèmes .


( Source )

L'effondrement de la fonction d'onde est un algorithme très indépendant qui ne nécessite pratiquement aucune aide ou instruction de l'extérieur. Vous n'avez besoin que d'un exemple du style que vous souhaitez atteindre, et il fera le reste. Malgré son autosuffisance, il est étonnamment simple. Il n'utilise pas de réseaux de neurones, de forêts aléatoires ou de tout ce qui ressemble à l'apprentissage automatique. Si vous traitez avec l'idée, elle deviendra très compréhensible et intuitive pour vous.

La plupart des implémentations et explications de l'effondrement de la fonction d'onde sont une version complète et optimisée de la vitesse de l'algorithme. Bien sûr, tous sont importants et nécessaires, mais il est difficile de les comprendre à partir de zéro. Dans cet article, je vais tout expliquer dans un langage simple que je comprends, en me concentrant sur la version limitée de Wavefunction, que j'ai appelée Even Simpler Tiled Model . De plus, j'ai publié un exemple d'implémentation d'ESTM sur Github . Le code qu'il contient est inefficace et lent, mais très lisible et commenté en détail. Dès que vous comprendrez la technologie sous-jacente ESTM, vous vous rapprocherez de la compréhension de versions plus complexes de l'algorithme. Si vous voulez comprendre l'algorithme d'effondrement de la fonction d'onde, cet article sera un bon début.

Commençons par l'histoire.

Le mariage

Imaginez que vous planifiez votre mariage. En plus de la sélection de bijoux et de musique, vous devez créer un plan de salle pour les invités pour le dîner. Votre famille aime discuter et être méchante, donc cela peut être difficile. Un père ne peut s'asseoir à moins de deux tables de sa mère. Un cousin devient solitaire s'il ne s'assoit pas avec un autre cousin. Et il vaut mieux ne pas planter Oncle Roy à côté des membres respectueux de l'environnement de la famille de votre partenaire. Il ne reste que 5 heures avant l'arrivée de la nourriture, vous décidez donc d'attaquer cette tâche tenace en utilisant l'algorithme d'effondrement de la fonction d'onde.

Vous commencez avec une longue liste de règles et un plan de salle vide.


Vous créez la fonction d'onde d' origine du plan. Elle lie chaque chaise à une liste de personnes qui peuvent s'y asseoir. Alors que toute personne peut s'asseoir sur n'importe quelle chaise. La fonction d'onde des sièges assis commence par une superposition complète (le concept est emprunté à la physique quantique) de chaque schéma possible.


Le chat de Schrödinger était mort et vivant en même temps jusqu'à ce que quelqu'un ouvre la boîte et vérifie; votre plan est en même temps tous les schémas possibles jusqu'à ce que vous mettiez les choses en ordre. Une superposition complète est une construction théorique utile, mais cela n'aidera pas votre grand-mère à comprendre où elle doit s'asseoir. Vous devez amener la fonction d'onde de l'emplacement des invités à un certain état, qui peut ensuite être transformé en cartes de visite ordinaires et non quantiques.

Nous commençons à le faire en effectuant l' effondrement de la fonction d'onde pour une chaise. Nous sélectionnons une chaise, examinons la liste des personnes qui peuvent s'y asseoir et l'assignons au hasard à l'une d'entre elles. Dans ce cas, la fonction d'onde du tabouret s'effondre.


Ce choix a des conséquences s'étendant aux fonctions d'onde des chaises restantes. Si l'oncle Roy est assis à la table 2, alors le cousin Frank et Michelle Obama (un ami de la famille de votre partenaire) ne seront certainement pas à côté de lui. Et si Michelle ne siège pas à la table 2, alors Barack ne sera pas non plus derrière lui. Nous mettons à jour la fonction d'onde du plan de localisation en supprimant des personnes des listes de candidats possibles.


Dès que les vibrations se sont calmées, nous répétons ce processus. Nous sélectionnons une autre chaise avec plusieurs candidats possibles et réduisons sa fonction d'onde, en choisissant au hasard l'une des personnes acceptables pour elle. Encore une fois, nous étendons les vibrations causées par ce choix au reste du plan, en retirant les gens de la fonction d'onde de la chaise s'ils ne peuvent plus s'y asseoir.

Nous répétons ce processus soit jusqu'à ce que la fonction d'onde s'effondre (c'est-à-dire qu'il ne reste plus qu'une personne assise), soit jusqu'à ce que nous arrivions à une contradiction . La contradiction est une chaise sur laquelle personne ne peut siéger, car ils ont tous été expulsés en raison des élections précédentes. La contradiction rend l'impossibilité de l'effondrement de la fonction d'onde entière.

Si vous avez atteint une contradiction, le plus simple est de recommencer. Jetez tous les travaux précédents, trouvez un nouveau plan vide et redémarrez l'algorithme, complétant l'effondrement de la fonction d'onde pour une autre chaise aléatoire. Vous pouvez également mettre en œuvre un système de retour en arrière qui vous permet d'annuler un choix particulier, plutôt que de tout abandonner immédiatement ("et si Sheila est transférée sur la chaise 54?").

Après quelques faux départs, vous atteindrez enfin un état complètement effondré dans lequel chaque chaise est attribuée à exactement une personne et toutes les règles sont suivies. C'est fait!

Du mariage aux bitmaps

Ce n'est pas un exemple théorique. Vous pouvez vraiment réaliser une variante de l'effondrement de la fonction d'onde, qui créera un plan de salle pour les invités pour le mariage. Cependant, dans l'effondrement de la fonction d'onde plus traditionnel, nous essayons généralement de ne pas asseoir les gens au mariage, mais de disposer les pixels dans l'image de sortie. Cependant, le processus sera très similaire. Nous enseignons à l'algorithme un ensemble de règles que la sortie doit satisfaire. Nous initialisons la fonction d'onde. Nous effectuons l'effondrement d'un élément et étendons les conséquences au reste de la fonction d'onde. Et nous continuons à le faire, soit jusqu'à ce que la fonction d'onde s'effondre complètement, soit jusqu'à ce que nous arrivions à une contradiction.

L'effondrement traditionnel de la fonction d'onde diffère de l'effondrement du mariage par la façon dont nous enseignons à l'algorithme les règles qu'il doit suivre. Dans la version mariage, nous devions écrire les règles nous-mêmes. Mais dans la version traditionnelle, nous donnons simplement à l'algorithme une image d'exemple, et sur cette base, l'algorithme crée le reste. Il analyse un exemple, analyse ses motifs et découvre comment les pixels ou les tuiles doivent s'aligner.

Commençons à rechercher l'effondrement réel d'une fonction d'onde en examinant un cas spécial simple, que ExUtumno (le créateur de l'algorithme) appelle le modèle en ExUtumno simple .

Modèle carrelé simple

Dans le modèle de tuile simple, les images d'entrée et de sortie sont construites à partir d'un petit nombre de tuiles prédéfinies, et chaque carré de l'image de sortie est limité à ses quatre voisins les plus proches. Par exemple, supposons que nous générions des mondes aléatoires pour un jeu à deux dimensions avec une vue de dessus. Nous pouvons avoir des tuiles pour la terre, la côte et la mer, ainsi qu'un ensemble de règles telles que «la côte peut être près de la mer», «la terre peut être près de la côte» et «la mer peut être à côté d'une autre mer».


Le modèle de tuile simple prend en compte la symétrie et la rotation de ses tuiles. Par exemple, la terre peut être près de la côte, mais uniquement dans le bon sens.


Ce traitement de symétrie fournit de meilleures images de sortie, mais complique le code. Pour garder les choses simples, regardons une vue encore plus simple de l'effondrement de la fonction d'onde, que j'ai appelé un modèle en mosaïque encore plus simple .

Modèle carrelé encore plus simple

Même le modèle de tuile plus simple («un modèle de tuile encore plus simple») est similaire au modèle de tuile simple, mais ses tuiles n'ont pas de propriétés de symétrie. Chaque tuile est un pixel de la même couleur, c'est-à-dire que nous ne pourrons en aucun cas confondre leurs bords.


Des règles de modèle de tuiles encore plus simples déterminent quelles tuiles peuvent être placées les unes à côté des autres et dans quelle orientation. Chaque règle est un tuple de trois éléments (3-tuple): deux tuiles et une direction. Par exemple, (SEA, COAST, LEFT) signifie que la tuile SEA (mer) peut être de la tuile COAST (côte). Cette règle doit être accompagnée d'une autre règle qui décrit la situation en termes de COAST - (COAST, SEA, RIGHT) .


Si vous voulez que les tuiles SEA soient situées non seulement vers la , mais aussi vers la depuis les tuiles COAST . alors ils ont besoin de règles supplémentaires: (SEA, COAST, RIGHT) et (COAST, SEA, LEFT) .

Comme je l'ai dit plus haut, nous n'avons pas besoin de créer nous-mêmes une liste de toutes ces règles. L'effondrement de la fonction d'onde peut créer un ensemble de règles pour le modèle de tuile encore plus simple en analysant une image d'exemple et en collectant une liste de tous les 3 tuples qu'elle contient.


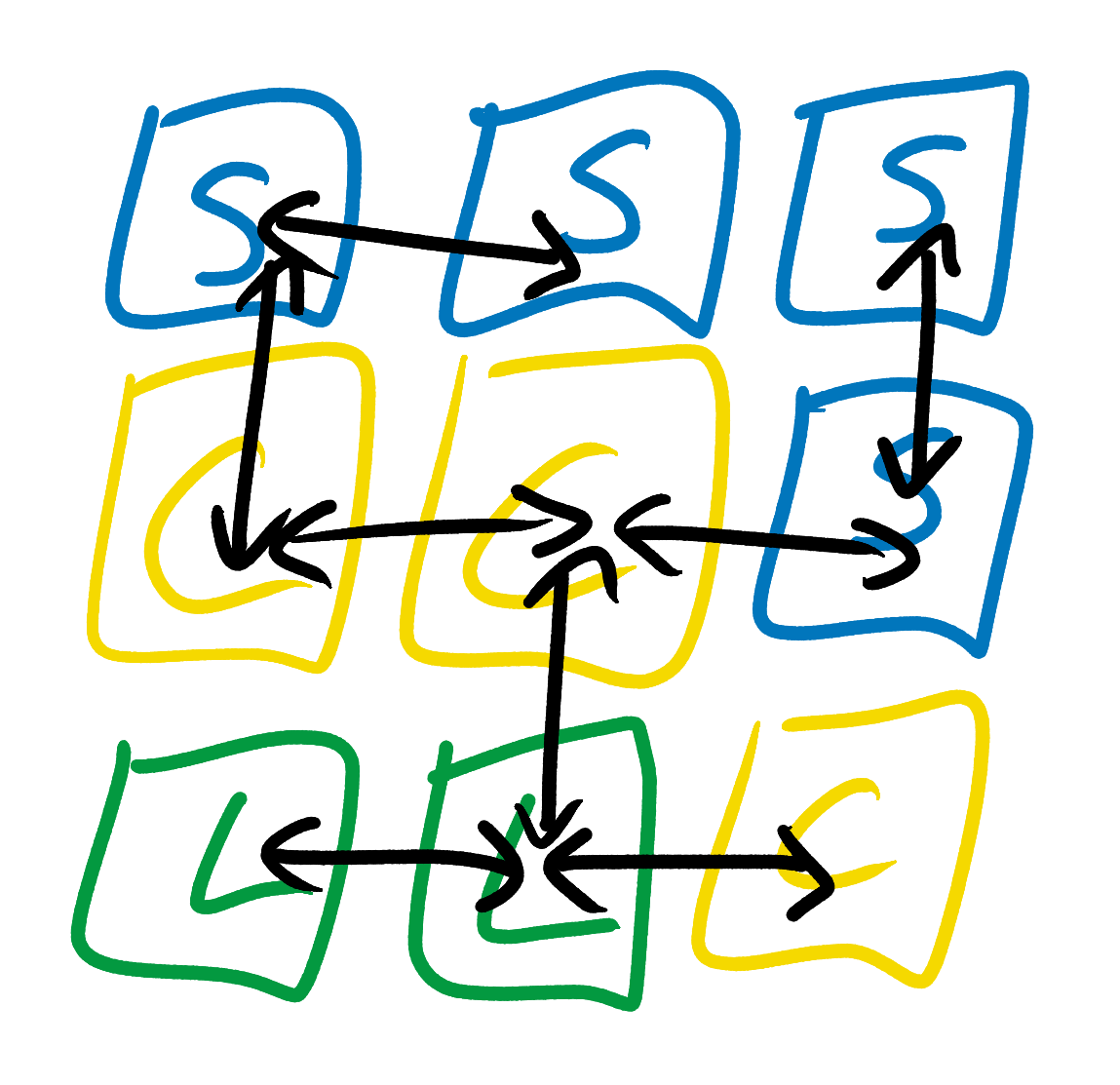
Après avoir examiné l'exemple d'image ci-dessus, le modèle de tuiles encore plus simple remarque que les tuiles de mer ne peuvent être que sous ou sur le côté des tuiles de côte, ou n'importe où près d'autres tuiles de mer. Elle note également que les tuiles côtières peuvent être situées à côté des tuiles terre, mer ou autres côtes, mais uniquement au-dessus des tuiles mer et sous les tuiles terre. Elle n'essaie pas de dériver de règles plus complexes, par exemple, "les tuiles de mer doivent être proches d'au moins une tuile de mer" ou "chaque île doit contenir au moins une tuile de terre". Aucune des tuiles ne peut affecter le fait que certains types de tuiles peuvent ou ne peuvent pas être situés à deux ou plusieurs carrés d'eux. Ceci est similaire à un modèle de plan de mariage dans lequel la seule règle est: "X peut s'asseoir à côté de Y".

Lors de l'analyse de l'image entrante, nous devons également enregistrer la fréquence à laquelle chacune des tuiles se rencontre. Plus tard, nous utilisons ces nombres comme poids lors du choix de la fonction d'onde du carré, dont l'effondrement doit être effectué, et également lors du choix de la tuile affectée au carré lors de son effondrement.

Après avoir appris les règles auxquelles l'image de sortie doit adhérer, nous sommes prêts à construire l'effondrement de la fonction d'onde de l'image de sortie.

Réduire

Comme dans l'exemple de mariage, nous commençons le processus d'effondrement avec une fonction d'onde dans laquelle chaque carré de l'image de sortie est en superposition de chaque type de carreau.


On commence par choisir un carré dont la fonction d'onde va s'effondrer. Dans l'exemple du mariage, ce choix a été fait par hasard. Cependant, comme l' ExUtumno noté ExUtumno , les gens abordent généralement ces tâches différemment. Au lieu de cela, ils recherchent des carrés avec l' entropie la plus faible. L'entropie est une mesure de l'incertitude et du désordre. En général, un carré à entropie élevée est un carré avec de nombreuses tuiles possibles restant dans sa fonction d'onde. On ne sait toujours pas à quelle tuile il s'effondre finalement. Un carré à faible entropie est un carré avec le moins de tuiles possible dans la fonction d'onde. L'ensemble des tuiles, à laquelle il s'effondre en conséquence, est déjà très limité.

Par exemple, dans le modèle de carreaux encore plus simple, un carré sans information sur les carrés environnants est illimité et peut devenir n'importe quel carreau. Par conséquent, il a une entropie très élevée. Mais un carré autour duquel plusieurs carrés se sont déjà effondrés peut avoir le choix de seulement 2 tuiles.


La fonction d'onde du carré central dans la figure ci-dessus ne s'est pas complètement effondrée, mais nous savons déjà qu'il ne peut pas s'agir d'une tuile terrestre. Cependant, il est déjà limité, ce qui signifie qu'il a une entropie inférieure à celle du carré supérieur droit, qui peut encore être terrestre, maritime ou côtier.

Ce sont des tuiles tellement limitées avec une faible entropie que les gens font généralement attention lorsqu'ils résolvent manuellement de tels problèmes. Même si vous n'utilisez pas l'effondrement de la fonction d'onde pour créer un plan pour accueillir les invités au mariage et que vous le rédigerez par vous-même, concentrez-vous toujours sur les zones du plan qui ont déjà le plus de restrictions. Vous ne mettrez pas Dwayne au tableau 1, puis vous sauterez au hasard pour obtenir Katie au tableau 7 (qui est vide jusqu'à présent). Vous mettez d'abord Dwayne, puis vous découvrirez qui peut s'asseoir à côté de lui, puis qui peut s'asseoir à côté de cette personne, et ainsi de suite. Je n'ai pas encore vu de justification à cela, mais mon intuition dit que l'utilisation de cette heuristique d'entropie minimale est susceptible de produire moins de contradictions que si vous sélectionnez au hasard des carrés pour l'effondrement.

La formule de Shannon est utilisée comme formule d'entropie dans l'algorithme d'effondrement de la fonction d'onde. Il utilise les poids des tuiles que nous avons analysés à partir de l'image entrante à l'étape précédente:

 # Sums are over the weights of each remaining # allowed tile type for the square whose # entropy we are calculating. shannon_entropy_for_square = log(sum(weight)) - (sum(weight * log(weight)) / sum(weight)) 

Après avoir calculé le carré de la fonction d'onde avec la plus petite entropie, nous réduisons sa fonction d'onde. Pour ce faire, nous choisissons au hasard l'une des tuiles qui sont toujours disponibles pour le carré, pondérée par le poids des tuiles que nous avons analysées à partir de l'image entrante. Les poids sont utilisés car ils fournissent une image de sortie plus réaliste. Supposons que la fonction d'onde d'un carré indique qu'il peut être terrestre ou côtier. Nous n'avons pas toujours à choisir l'une des options avec une probabilité de 50%. Si l'image d'entrée a plus de tuiles terrestres que la côte, alors nous devons refléter cet avantage dans l'image de sortie. Ceci est réalisé en utilisant des poids globaux simples. Si, dans l'image d'exemple, il y a 20 tuiles terre et 10 tuiles côte, alors le carré s'effondre en terre avec une probabilité de 2/3 , et en côte avec une probabilité restante de 1/3 .

Ensuite, nous étendons les conséquences du choix au reste de la fonction d'onde de la sortie ("si cette tuile s'est avérée être la mer, alors cette tuile ne peut pas être la terre, c'est-à-dire que cela ne peut pas être la côte"). Lorsque tous ces tremblements se sont installés, nous répétons le processus en utilisant l'heuristique d'entropie minimale pour sélectionner la tuile qui s'effondre suivante. Nous répétons ce cycle d'effondrement-propagation, soit jusqu'à ce que toute la fonction d'onde de l'image de sortie s'effondre complètement et que nous puissions retourner le résultat, ou jusqu'à ce que nous atteignions une contradiction et renvoyions une erreur.

En conséquence, nous avons créé un monde (ou une erreur).

Où aller ensuite

Après avoir traité du modèle en mosaïque encore plus simple, vous êtes prêt à gravir les échelons de la puissance et de la complexité de l'algorithme. Commencez avec le modèle simple en mosaïque que nous avons mentionné au début de cet article, puis passez au modèle de chevauchement complet. Dans le modèle à chevauchement, les tuiles ou les pixels s’affectent à distance. Si vous comprenez de telles choses, ExUtumno remarque que le modèle en ExUtumno simple est similaire à la chaîne Markov d'ordre 1, et les modèles plus complexes ressemblent à des chaînes d'ordre plus important.

L'effondrement de la fonction d'onde peut même prendre en compte des restrictions supplémentaires, par exemple, "cette tuile doit être mer" ou "ce pixel doit être rouge" ou "il ne peut y avoir qu'un seul monstre dans la sortie". Tout cela est décrit dans le README du projet principal . Vous pouvez également étudier les optimisations de vitesse apportées à l'implémentation complète. Il n'est pas nécessaire de recalculer l'entropie de chaque carré à chaque itération, et la diffusion des informations par la fonction d'onde peut se faire beaucoup plus rapidement. Ces aspects deviennent plus importants à mesure que la taille des images de sortie augmente.

L'effondrement de la fonction d'onde est un outil magnifique et puissant qui mérite d'être maîtrisé. Pensez-y la prochaine fois que vous planifiez un mariage ou générez un monde procédural.