Réseaux de neurones et apprentissage profond, Chapitre 4: Preuve visuelle que les réseaux de neurones peuvent calculer n'importe quelle fonction

Dans ce chapitre, je donne une explication simple et surtout visuelle du théorème de l'universalité. Pour suivre le contenu de ce chapitre, il n'est pas nécessaire de lire les précédents. Il est structuré comme un essai indépendant. Si vous avez la compréhension la plus élémentaire de NS, vous devriez être capable de comprendre les explications.


L'un des faits les plus étonnants sur les réseaux de neurones est qu'ils peuvent calculer n'importe quelle fonction. Autrement dit, supposons que quelqu'un vous donne une sorte de fonction complexe et sinueuse f (x):



Et quelle que soit cette fonction, il est garanti un réseau de neurones tel que pour toute entrée x la valeur f (x) (ou une approximation proche) sera la sortie de ce réseau, c'est-à-dire:



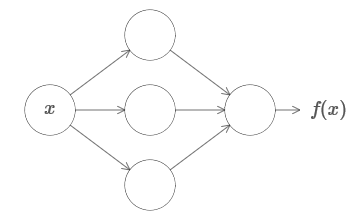
Cela fonctionne même si c'est une fonction de nombreuses variables f = f (x ₁ , ..., x _m ), et avec de nombreuses valeurs. Par exemple, voici un réseau calculant une fonction avec m = 3 entrées et n = 2 sorties:



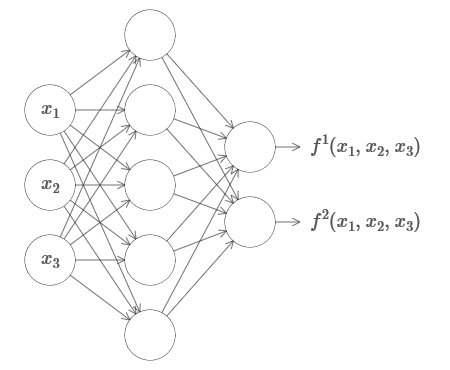
Ce résultat suggère que les réseaux de neurones ont une certaine universalité. Quelle que soit la fonction que nous voulons calculer, nous savons qu'il existe un réseau neuronal qui peut le faire.

De plus, le théorème d'universalité tient même si nous limitons le réseau à une seule couche entre les neurones entrants et sortants - ce qu'on appelle dans une couche cachée. Ainsi, même les réseaux avec une architecture très simple peuvent être extrêmement puissants.

Le théorème de l'universalité est bien connu des personnes utilisant des réseaux de neurones. Mais bien qu'il en soit ainsi, la compréhension de ce fait n'est pas si répandue. Et la plupart des explications à cela sont trop complexes sur le plan technique. Par exemple, l' un des premiers articles prouvant ce résultat a utilisé le théorème de Hahn-Banach , le théorème de représentation de Riesz et une analyse de Fourier. Si vous êtes mathématicien, il est facile pour vous de comprendre ces preuves, mais pour la plupart des gens, ce n'est pas si facile. C’est dommage, car les raisons fondamentales de l’universalité sont simples et belles.

Dans ce chapitre, je donne une explication simple et surtout visuelle du théorème de l'universalité. Nous allons parcourir pas à pas les idées qui le sous-tendent. Vous comprendrez pourquoi les réseaux de neurones peuvent vraiment calculer n'importe quelle fonction. Vous comprendrez certaines des limites de ce résultat. Et vous comprendrez comment le résultat est associé à une NS profonde.

Pour suivre le contenu de ce chapitre, il n'est pas nécessaire de lire les précédents. Il est structuré comme un essai indépendant. Si vous avez la compréhension la plus élémentaire de NS, vous devriez être capable de comprendre les explications. Mais je fournirai parfois des liens vers des documents précédents pour aider à combler les lacunes dans les connaissances.

Les théorèmes d'universalité se trouvent souvent en informatique, alors parfois nous oublions même à quel point ils sont incroyables. Mais cela vaut la peine de vous le rappeler: la capacité de calculer n'importe quelle fonction arbitraire est vraiment incroyable. Presque tous les processus que vous pouvez imaginer peuvent être réduits au calcul d'une fonction. Considérez la tâche de trouver le nom d'une composition musicale sur la base d'un bref passage. Cela peut être considéré comme un calcul de fonction. Ou considérez la tâche de traduire un texte chinois en anglais. Et cela peut être considéré comme un calcul de fonction (en fait, de nombreuses fonctions, car il existe de nombreuses options acceptables pour traduire un seul texte). Ou considérez la tâche de générer une description de l'intrigue du film et de la qualité du jeu sur la base du fichier mp4. Cela aussi peut être considéré comme le calcul d'une certaine fonction (la remarque faite sur les options de traduction de texte est également correcte ici). L'universalité signifie qu'en principe, les SN peuvent effectuer toutes ces tâches et bien d'autres.

Bien sûr, seulement du fait que nous savons qu'il existe des NS capables de traduire, par exemple, du chinois vers l'anglais, il ne s'ensuit pas que nous ayons de bonnes techniques pour créer ou même reconnaître un tel réseau. Cette restriction s'applique également aux théorèmes d'universalité traditionnels pour les modèles tels que les schémas booléens. Mais, comme nous l'avons déjà vu dans ce livre, le NS dispose de puissants algorithmes d'apprentissage des fonctions. La combinaison d'algorithmes d'apprentissage et de polyvalence est un mélange attrayant. Jusqu'à présent, dans le livre, nous nous sommes concentrés sur les algorithmes de formation. Dans ce chapitre, nous nous concentrerons sur la polyvalence et ce que cela signifie.

Deux astuces

Avant d'expliquer pourquoi le théorème d'universalité est vrai, je veux mentionner deux astuces contenues dans l'énoncé informel «un réseau de neurones peut calculer n'importe quelle fonction».

Premièrement, cela ne signifie pas que le réseau peut être utilisé pour calculer avec précision n'importe quelle fonction. Nous pouvons obtenir une approximation aussi bonne que nécessaire. En augmentant le nombre de neurones cachés, nous améliorons l'approximation. Par exemple, j'ai précédemment illustré un réseau calculant une certaine fonction f (x) en utilisant trois neurones cachés. Pour la plupart des fonctions, en utilisant trois neurones, seule une approximation de faible qualité peut être obtenue. En augmentant le nombre de neurones cachés (disons, jusqu'à cinq), nous pouvons généralement obtenir une meilleure approximation:



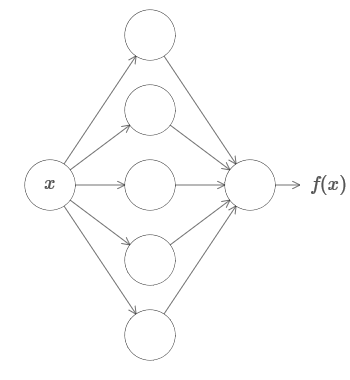
Et pour améliorer la situation en augmentant encore le nombre de neurones cachés.

Pour clarifier cette affirmation, disons qu'on nous a donné une fonction f (x), que nous voulons calculer avec une certaine précision nécessaire ε> 0. Il est garanti qu'en utilisant un nombre suffisant de neurones cachés, nous pouvons toujours trouver un NS dont la sortie g (x) satisfait l'équation | g (x) −f (x) | <ε pour tout x. En d'autres termes, l'approximation sera réalisée avec la précision souhaitée pour toute valeur d'entrée possible.

Le deuxième problème est que les fonctions qui peuvent être approximées par la méthode décrite appartiennent à une classe continue. Si la fonction est interrompue, c'est-à-dire qu'elle fait des sauts brusques et soudains, alors dans le cas général, il sera impossible de se rapprocher à l'aide de NS. Et cela n'est pas surprenant, car nos NS calculent les fonctions continues des données d'entrée. Cependant, même si la fonction que nous devons vraiment calculer est discontinue, l'approximation est souvent assez continue. Si oui, alors nous pouvons utiliser NS. En pratique, cette limitation n'est généralement pas importante.

En conséquence, une déclaration plus précise du théorème d'universalité sera que NS avec une couche cachée peut être utilisée pour approximer n'importe quelle fonction continue avec la précision souhaitée. Dans ce chapitre, nous prouvons une version légèrement moins rigoureuse de ce théorème, utilisant deux couches cachées au lieu d'une. Dans les tâches, je décrirai brièvement comment cette explication peut être adaptée, avec des modifications mineures, à une preuve qui utilise une seule couche cachée.

Polyvalence avec une entrée et une valeur de sortie

Pour comprendre pourquoi le théorème d'universalité est vrai, nous commençons par comprendre comment créer une fonction d'approximation NS avec une seule entrée et une seule valeur de sortie:



Il s'avère que c'est l'essence même de la tâche d'universalité. Une fois que nous aurons compris ce cas particulier, il sera assez facile de l'étendre à des fonctions avec de nombreuses valeurs d'entrée et de sortie.

Pour comprendre comment construire un réseau pour compter f, nous commençons avec un réseau contenant une seule couche cachée avec deux neurones cachés, et avec une couche de sortie contenant un neurone de sortie:



Pour imaginer comment fonctionnent les composants du réseau, nous nous concentrons sur le neurone supérieur caché. Dans le diagramme de l' article d'origine, vous pouvez modifier le poids de manière interactive avec la souris en cliquant sur «w» et voir immédiatement comment la fonction calculée par le neurone supérieur caché change:



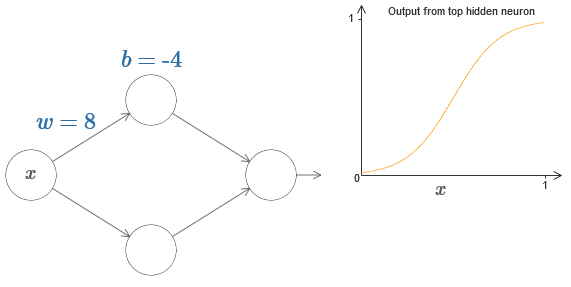
Comme nous l'avons appris plus tôt dans le livre, un neurone caché compte σ (wx + b), où σ (z) ≡ 1 / (1 + e ^−z ) est un sigmoïde . Jusqu'à présent, nous avons utilisé cette forme algébrique assez souvent. Cependant, pour prouver l'universalité, il serait préférable d'ignorer complètement cette algèbre et de manipuler et d'observer la forme sur le graphique. Cela vous aidera non seulement à mieux ressentir ce qui se passe, mais nous donnera également une preuve d'universalité applicable à d'autres fonctions d'activation en plus de sigmoïde.

À strictement parler, l'approche visuelle que j'ai choisie n'est traditionnellement pas considérée comme une preuve. Mais je crois que l'approche visuelle fournit plus de perspicacité dans la vérité du résultat final que la preuve traditionnelle. Et, bien sûr, une telle compréhension est le véritable objectif de la preuve. Dans les preuves que je propose, des lacunes se présenteront parfois; Je fournirai des preuves visuelles raisonnables, mais pas toujours rigoureuses. Si cela vous dérange, considérez qu'il est de votre devoir de combler ces lacunes. Cependant, ne perdons pas de vue l'objectif principal: comprendre pourquoi le théorème de l'universalité est vrai.

Pour commencer avec cette épreuve, cliquez sur le décalage b dans le diagramme d'origine et faites glisser vers la droite pour l'agrandir. Vous verrez qu'avec une augmentation du décalage, le graphique se déplace vers la gauche, mais ne change pas de forme.

Faites-le ensuite glisser vers la gauche pour réduire le décalage. Vous verrez que le graphique se déplace vers la droite sans changer de forme.

Réduisez le poids à 2-3. Vous verrez qu'à mesure que le poids diminue, la courbe se redresse. Pour que la courbe ne s'échappe pas du graphique, vous devrez peut-être corriger le décalage.

Enfin, augmentez le poids à des valeurs supérieures à 100. La courbe deviendra plus raide et finira par s'approcher de l'étape. Essayez d'ajuster le décalage de sorte que son angle soit dans la région du point x = 0,3. La vidéo ci-dessous montre ce qui devrait arriver:



Nous pouvons grandement simplifier notre analyse en augmentant le poids afin que la sortie soit vraiment une bonne approximation de la fonction de pas. Ci-dessous, j'ai construit la sortie du neurone caché supérieur pour le poids w = 999. Ceci est une image statique:



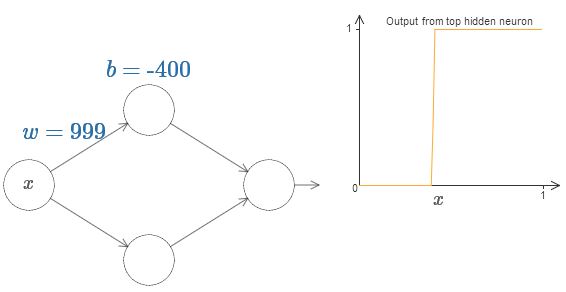
L'utilisation des fonctions pas à pas est un peu plus facile qu'avec un sigmoïde typique. La raison en est que les contributions de tous les neurones cachés sont additionnées dans la couche de sortie. La somme d'un ensemble de fonctions pas à pas est facile à analyser, mais il est plus difficile de parler de ce qui se passe lorsqu'un groupe de courbes est ajouté en tant que sigmoïde. Par conséquent, il sera beaucoup plus simple de supposer que nos neurones cachés produisent des fonctions pas à pas. Plus précisément, nous le faisons en fixant le poids w à une valeur très élevée, puis en affectant la position du pas à travers le décalage. Bien sûr, travailler avec une sortie en tant que fonction pas à pas est une approximation, mais c'est très bien, et jusqu'à présent, nous traiterons la fonction comme une vraie fonction pas à pas. Plus tard, je reviendrai sur la discussion de l'effet des écarts par rapport à cette approximation.

Quelle valeur de x est le pas? En d'autres termes, comment la position de la marche dépend-elle du poids et du déplacement?

Pour répondre à la question, essayez de modifier le poids et le décalage dans le graphique interactif. Pouvez-vous comprendre comment la position de l'étape dépend de w et b? En pratiquant un peu, vous pouvez vous convaincre que sa position est proportionnelle à b et inversement proportionnelle à w.

En fait, le pas est à s = ​​−b / w, comme on le verra si on ajuste le poids et le déplacement aux valeurs suivantes:



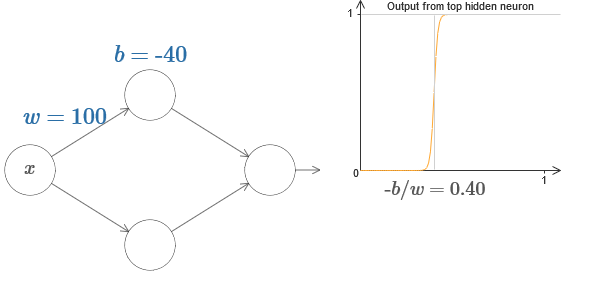
Notre vie sera grandement simplifiée si nous décrivons des neurones cachés avec un seul paramètre, s, c'est-à-dire par la position du pas, s = −b / w. Dans le diagramme interactif suivant, vous pouvez simplement modifier s:



Comme indiqué ci-dessus, nous avons spécialement attribué un poids w à l'entrée à une très grande valeur - suffisamment grande pour que la fonction de pas devienne une bonne approximation. Et nous pouvons facilement ramener le neurone paramétré de cette manière à sa forme habituelle en choisissant le biais b = −ws.

Jusqu'à présent, nous nous sommes concentrés sur la sortie du seul neurone caché supérieur. Examinons le comportement de l'ensemble du réseau. Supposons que les neurones cachés calculent les fonctions de pas définies par les paramètres des pas s ₁ (neurone supérieur) et s ₂ (neurone inférieur). Leurs poids de sortie respectifs sont w ₁ et w ₂ . Voici notre réseau:



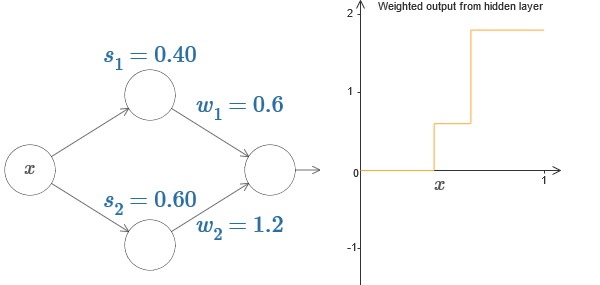
À droite, un graphique de la sortie pondérée w ₁ a ₁ + w ₂ a _{2 de la} couche cachée. Ici, a ₁ et a ₂ sont respectivement les sorties des neurones cachés supérieur et inférieur. Ils sont désignés par «a», car ils sont souvent appelés activations neuronales.

Soit dit en passant, nous notons que la sortie de l'ensemble du réseau est σ (w ₁ a ₁ + w ₂ a ₂ + b), où b est le biais du neurone de sortie. Ce n'est évidemment pas la même chose que la sortie pondérée de la couche cachée, dont nous construisons le graphique. Mais pour l'instant, nous nous concentrerons sur la sortie équilibrée de la couche cachée et ne penserons que plus tard à la façon dont elle se rapporte à la sortie de l'ensemble du réseau.

Essayez d'augmenter et de diminuer l'étape s _{1 du} neurone supérieur caché sur le diagramme interactif dans l'article d'origine . Découvrez comment cela modifie la sortie pondérée du calque masqué. Il est particulièrement utile de comprendre ce qui se passe lorsque s ₁ dépasse s ₂ . Vous verrez que le graphique dans ces cas change de forme, lorsque nous passons d'une situation dans laquelle le neurone caché supérieur est activé en premier à une situation dans laquelle le neurone caché inférieur est activé en premier.

De même, essayez de manipuler le pas s _{2 du} neurone caché inférieur et voyez comment cela modifie la sortie globale des neurones cachés.

Essayez de réduire et d'augmenter les poids de sortie. Remarquez comment cela modifie la contribution des neurones cachés correspondants. Que se passe-t-il si l'un des poids est égal à 0?

Enfin, essayez de régler w ₁ à 0,8 et w ₂ à -0,8. Le résultat est une fonction de «saillie», avec un début à s ₁ , une fin à s ₂ et une hauteur de 0,8. Par exemple, une sortie pondérée pourrait ressembler à ceci:



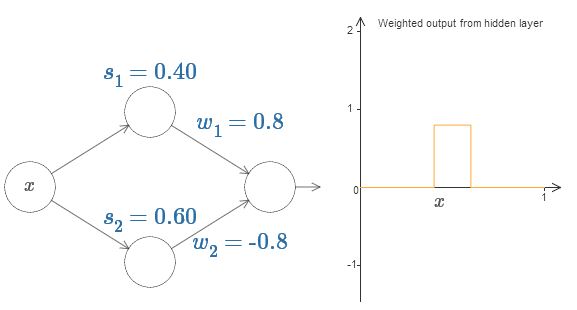
Bien sûr, la saillie peut être mise à l'échelle à n'importe quelle hauteur. Utilisons un paramètre, h, indiquant la hauteur. Aussi, pour simplifier, je vais me débarrasser des notations "s ₁ = ..." et "w ₁ = ...".



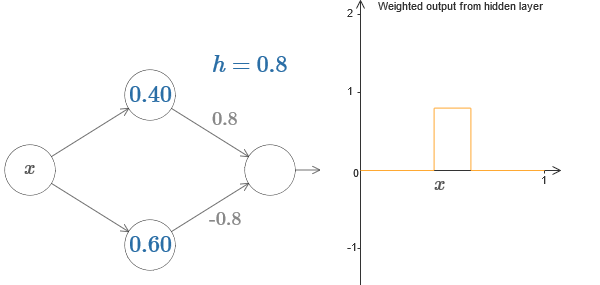
Essayez d'augmenter et de diminuer la valeur h pour voir comment la hauteur de la saillie change. Essayez de rendre h négatif. Essayez de modifier les points des étapes pour observer comment cela modifie la forme de la saillie.

Vous verrez que nous utilisons nos neurones non seulement comme des primitives graphiques, mais aussi comme des unités plus familières aux programmeurs - quelque chose comme une instruction si-alors-autre dans la programmation:

si entrée> = début de l'étape:
ajouter 1 à la sortie pondérée
sinon:
ajouter 0 à la sortie pondérée

Pour la plupart, je m'en tiendrai à la notation graphique. Cependant, il vous sera parfois utile de passer à la vue si-alors-autre et de réfléchir à ce qui se passe en ces termes.

Nous pouvons utiliser notre astuce de protrusion en collant deux parties de neurones cachés ensemble sur le même réseau:



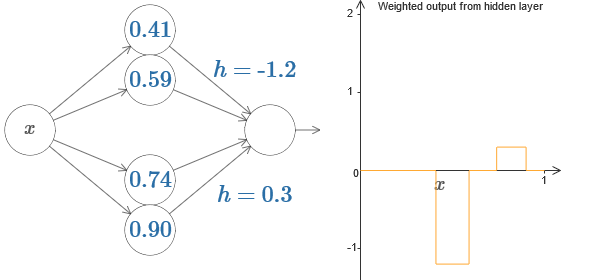
Ici, j'ai baissé les poids en écrivant simplement les valeurs h pour chaque paire de neurones cachés. Essayez de jouer avec les deux valeurs h et voyez comment cela change le graphique. Déplacez les onglets, en changeant les points des étapes.

Dans un cas plus général, cette idée peut être utilisée pour obtenir un nombre souhaité de pics de n'importe quelle hauteur. En particulier, nous pouvons diviser l'intervalle [0,1] en un grand nombre de (N) sous-intervalles, et utiliser N paires de neurones cachés pour obtenir des pics de n'importe quelle hauteur souhaitée. Voyons comment cela fonctionne pour N = 5. C'est déjà beaucoup de neurones, donc je suis une présentation un peu plus étroite. Désolé pour le diagramme complexe - j'ai pu cacher la complexité derrière des abstractions supplémentaires, mais il me semble que cela vaut la peine d'être tourmenté par la complexité afin de mieux ressentir le fonctionnement des réseaux de neurones.



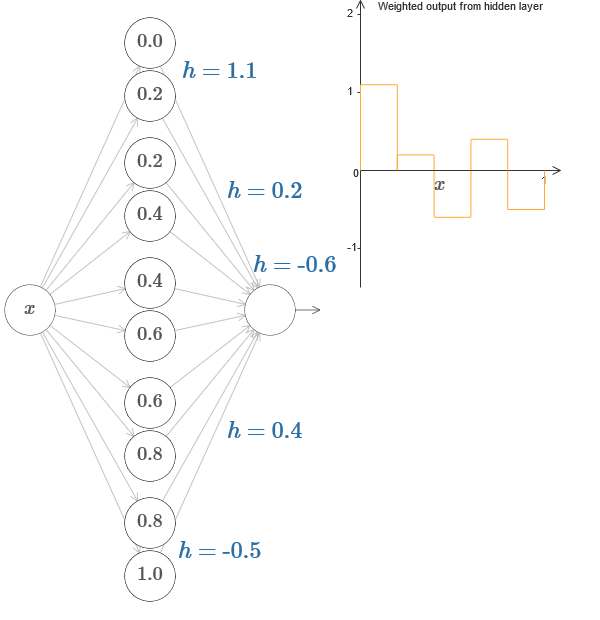
Vous voyez, nous avons cinq paires de neurones cachés. Les points des pas des paires correspondantes sont situés à 0,1 / 5, puis 1 / 5,2 / 5, et ainsi de suite, jusqu'à 4 / 5,5 / 5. Ces valeurs sont fixes - nous obtenons cinq protubérances de largeur égale sur le graphique.

Chaque paire de neurones a une valeur h qui lui est associée. N'oubliez pas que les connexions des neurones de sortie ont des poids h et –h. Dans l'article d'origine du graphique, vous pouvez cliquer sur les valeurs h et les déplacer de gauche à droite. Avec un changement de hauteur, l'horaire change également. En modifiant les poids de sortie, nous construisons la fonction finale!

Sur le diagramme, vous pouvez toujours cliquer sur le graphique et faire glisser la hauteur des marches vers le haut ou vers le bas. Lorsque vous modifiez sa hauteur, vous voyez comment la hauteur du h correspondant change. Les poids de sortie + h et –h changent en conséquence. En d'autres termes, nous manipulons directement une fonction dont le graphique est affiché à droite et voyons ces changements dans les valeurs de h à gauche. Vous pouvez également maintenir le bouton de la souris enfoncé sur l'une des saillies, puis faire glisser la souris vers la gauche ou la droite, et les saillies s'ajusteront à la hauteur actuelle.

Il est temps de faire le travail.

Rappelez-vous la fonction que j'ai dessinée au tout début du chapitre:



Ensuite, je n'ai pas mentionné cela, mais en fait, cela ressemble à ceci:

$$

$$f (x) = 0,2 + 0,4 x ^ 2 + 0,3x \ sin (15 x) + 0,05 \ cos (50 x) \ tag {113}$$

Il est construit pour x valeurs de 0 à 1, et les valeurs le long de l'axe y varient de 0 à 1.

De toute évidence, cette fonction n'est pas triviale. Et vous devez comprendre comment le calculer en utilisant des réseaux de neurones.

Dans nos réseaux de neurones ci-dessus, nous avons analysé une combinaison pondérée ∑ _j w _j a _j de sortie de neurones cachés. Nous savons comment contrôler significativement cette valeur. Mais, comme je l'ai noté précédemment, cette valeur n'est pas égale à la sortie réseau. La sortie du réseau est σ (∑ _j w _j a _j + b), où b est le déplacement du neurone de sortie. Pouvons-nous prendre le contrôle directement sur la sortie du réseau?

La solution consiste à développer un réseau neuronal dans lequel la sortie pondérée de la couche cachée est donnée par l'équation σ ⁻¹ ⋅f (x), où σ ⁻¹ est la fonction inverse de σ. Autrement dit, nous voulons que la sortie pondérée de la couche cachée soit la suivante:



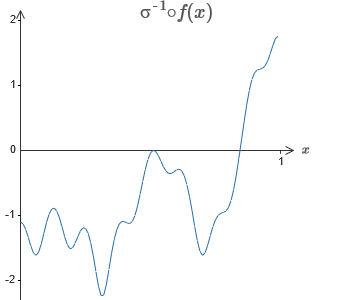Si cela réussit, alors la sortie de l'ensemble du réseau sera une bonne approximation de f (x) (j'ai réglé le décalage du neurone de sortie sur 0).

Ensuite, votre tâche consiste à développer une NS approximative de la fonction objectif indiquée ci-dessus. Pour mieux comprendre ce qui se passe, je vous recommande de résoudre ce problème deux fois. Pour la première fois dans l' article original, cliquez sur le graphique et ajustez directement les hauteurs des différentes saillies. Il vous sera assez facile d'obtenir une bonne approximation de la fonction objectif. Le degré d'approximation est estimé par l'écart moyen, la différence entre la fonction objectif et la fonction que le réseau calcule. Votre tâche consiste à ramener l'écart moyen à une valeur minimale. La tâche est considérée comme terminée lorsque l'écart moyen ne dépasse pas 0,40.



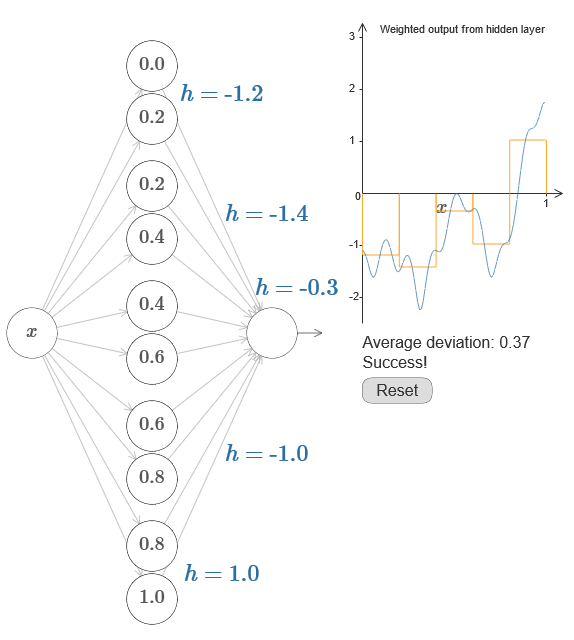Après avoir réussi, appuyez sur le bouton Réinitialiser, qui modifie les onglets de manière aléatoire. La deuxième fois, ne touchez pas le graphique, mais modifiez les valeurs h sur le côté gauche du diagramme, en essayant de ramener l'écart moyen à une valeur de 0,40 ou moins.

Et donc, vous avez trouvé tous les éléments nécessaires au réseau pour calculer approximativement la fonction f (x)! L'approximation s'est avérée grossière, mais nous pouvons facilement améliorer le résultat en augmentant simplement le nombre de paires de neurones cachés, ce qui augmentera le nombre de protubérances.

En particulier, il est facile de reconvertir toutes les données trouvées dans la vue standard avec le paramétrage utilisé pour NS. Permettez-moi de vous rappeler rapidement comment cela fonctionne.

Dans la première couche, tous les poids ont une grande valeur constante, par exemple, w = 1000.

Les déplacements des neurones cachés sont calculés par b = −ws. Ainsi, par exemple, pour le deuxième neurone caché, s = 0,2 se transforme en b = −1000 × 0,2 = −200.

La dernière couche de l'échelle est déterminée par les valeurs de h. Ainsi, par exemple, la valeur que vous choisissez pour le premier h, h = -0,2, signifie que les poids de sortie des deux neurones supérieurs cachés sont respectivement -0,2 et 0,2. Et ainsi de suite, pour toute la couche de poids de sortie.

Enfin, le décalage du neurone de sortie est 0.

Et c'est tout: nous avons une description complète du NS, qui calcule bien la fonction objectif initiale. Et nous comprenons comment améliorer la qualité de l'approximation en améliorant le nombre de neurones cachés.

De plus, dans notre fonction objectif d'origine f (x) = 0,2 + 0,4x ²+ 0.3sin (15x) + 0.05cos (50x) n'a rien de spécial. Une procédure similaire pourrait être utilisée pour toute fonction continue sur les intervalles de [0,1] à [0,1]. En fait, nous utilisons notre NS à couche unique pour construire une table de recherche pour une fonction. Et nous pouvons prendre cette idée comme base pour obtenir une preuve généralisée d'universalité.

Fonction de nombreux paramètres

Nous étendons nos résultats au cas d'un ensemble de variables d'entrée. Cela semble compliqué, mais toutes les idées dont nous avons besoin peuvent déjà être comprises pour le cas avec seulement deux variables entrantes. Par conséquent, nous considérons le cas avec deux variables entrantes.

Commençons par regarder ce qui se passe quand un neurone a deux entrées: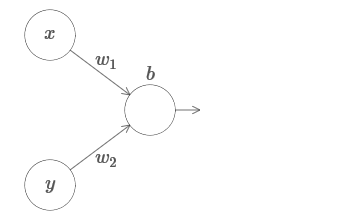



Nous avons les entrées x et y, avec les poids correspondants w ₁ et w ₂ et le décalage b du neurone. Définissez le poids de w ₂ sur 0 et jouez avec le premier, w ₁ et le décalage b pour voir comment ils affectent la sortie du neurone:



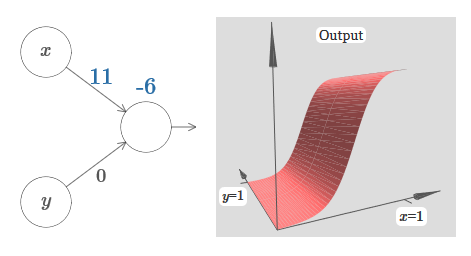Comme vous pouvez le voir, avec w ₂ = 0, l'entrée y n'affecte pas la sortie du neurone. Tout se passe comme si x était la seule entrée.

Compte tenu de cela, que pensez-vous qu'il se passera lorsque nous augmenterons le poids de w ₁ à w ₁ = 100 et que w ₂ laissera 0? Si cela ne vous est pas immédiatement clair, réfléchissez un peu à cette question. Regardez ensuite la vidéo suivante, qui montre ce qui va se passer:



Comme précédemment, avec une augmentation du poids d'entrée, la sortie se rapproche de la forme de l'étape. La différence est que notre fonction pas à pas est maintenant située en trois dimensions. Comme précédemment, nous pouvons déplacer l'emplacement des étapes en modifiant le décalage. L'angle sera au point s _x ≡ - b / w1.

Reprenons le diagramme pour que le paramètre soit l'emplacement de l'étape:



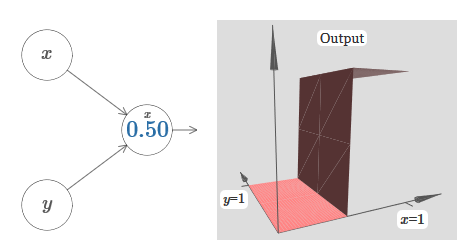Nous supposons que le poids d'entrée de x est d'une grande importance - j'ai utilisé w ₁ = 1000 - et le poids w ₂ = 0. Le nombre sur le neurone est la position du pas, et le x au-dessus nous rappelle que nous déplaçons le pas le long de l'axe x. Naturellement, il est tout à fait possible d'obtenir une fonction de pas le long de l'axe y, ce qui rend le poids entrant pour y grand (par exemple, w ₂= 1000), et le poids pour x est 0, w ₁ = 0:



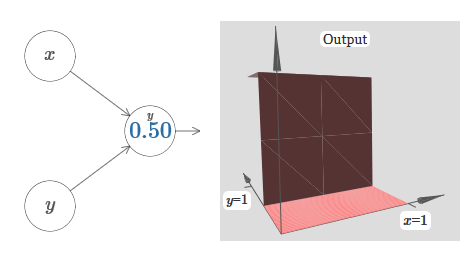Le nombre sur le neurone, encore une fois, indique la position du pas, et y au-dessus nous rappelle que nous déplaçons le pas le long de l'axe y. Je pourrais directement désigner les poids pour x et y, mais je ne l'ai pas fait, car cela jetterait le graphique. Mais gardez à l'esprit que le marqueur y indique que le poids pour y est grand et pour x est 0.

Nous pouvons utiliser les fonctions de pas que nous venons de concevoir pour calculer la fonction de saillie tridimensionnelle. Pour ce faire, nous prenons deux neurones, chacun calculant une fonction de pas le long de l'axe x. Ensuite, nous combinons ces fonctions de pas avec les poids h et –h, où h est la hauteur de saillie souhaitée. Tout cela peut être vu dans le diagramme suivant:



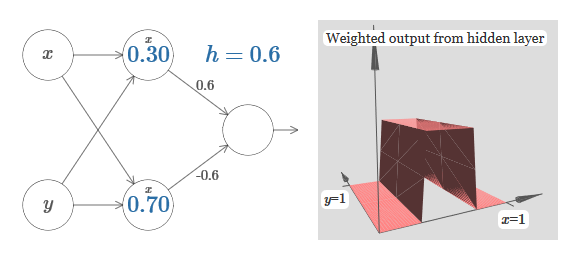Essayez de modifier la valeur de h. Voyez comment cela se rapporte aux poids du réseau. Et comment elle modifie la hauteur de la fonction de saillie à droite.

Essayez également de modifier le point de l'étape, dont la valeur est définie sur 0,30 dans le neurone supérieur caché. Voyez comment cela change la forme de la saillie. Que se passe-t-il si vous le déplacez au-delà du point 0,70 associé au neurone caché inférieur?

Nous avons appris à construire la fonction de protrusion le long de l'axe x. Naturellement, nous pouvons facilement faire la fonction de saillie le long de l'axe y, en utilisant deux fonctions de pas le long de l'axe y. Rappelons que nous pouvons le faire en faisant de grands poids à l'entrée y et en réglant le poids 0 à l'entrée x. Et alors, que se passe-t-il:



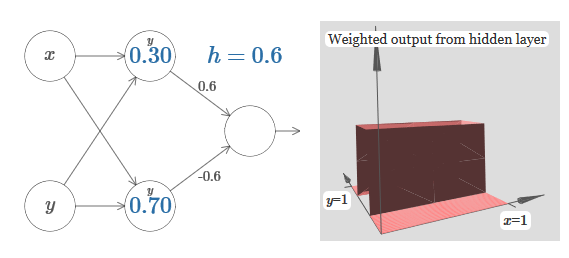Il semble presque identique au réseau précédent! Le seul changement visible est de petits marqueurs y sur les neurones cachés. Ils nous rappellent qu'ils produisent des fonctions pas à pas pour y, et non pour x, donc le poids à l'entrée y est très grand, et à l'entrée x il est nul, et non l'inverse. Comme précédemment, j'ai décidé de ne pas le montrer directement, afin de ne pas encombrer l'image.

Voyons ce qui se passe si nous ajoutons deux fonctions de protrusion, l'une le long de l'axe x, l'autre le long de l'axe y, toutes deux de hauteur h:



Pour simplifier le schéma de connexion avec un poids nul, j'ai omis. Jusqu'à présent, j'ai laissé de petits marqueurs x et y sur les neurones cachés pour me rappeler dans quelles directions les fonctions de protrusion sont calculées. Plus tard, nous les refuserons, car ils sont impliqués par la variable entrante.

Essayez de changer le paramètre h. Comme vous pouvez le voir, pour cette raison, les poids de sortie changent, ainsi que les poids des deux fonctions de saillie, x et y.

Notre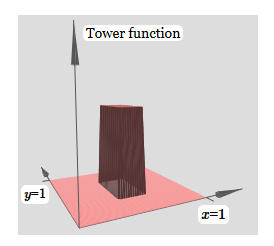



création est un peu comme une «fonction tour»: si nous pouvons créer de telles fonctions tour, nous pouvons les utiliser pour approximer des fonctions arbitraires en ajoutant simplement des tours de différentes hauteurs à différents endroits:



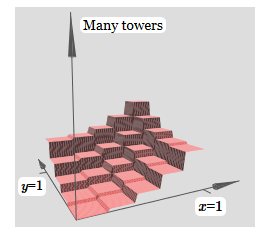bien sûr, nous n'avons pas encore atteint la création d'une fonction tour arbitraire. Jusqu'à présent, nous avons construit quelque chose comme une tour centrale de hauteur 2h avec un plateau de hauteur h qui l'entoure.

Mais nous pouvons faire fonctionner une tour. Rappelons que nous avons précédemment montré comment les neurones peuvent être utilisés pour implémenter l'instruction if-then-else:

if  >= :  1 else:  0 

C'était un neurone à une entrée. Et nous devons appliquer une idée similaire à la sortie combinée des neurones cachés:

  if     >= :  1 else:  0 

Si nous choisissons le bon seuil - par exemple, 3h / 2, coincé entre la hauteur du plateau et la hauteur de la tour centrale - nous pouvons écraser le plateau à zéro et ne laisser qu'une seule tour.

Imaginez comment faire cela? Essayez d'expérimenter avec le réseau suivant. Maintenant, nous traçons la sortie de l'ensemble du réseau, et pas seulement la sortie pondérée de la couche cachée. Cela signifie que nous ajoutons le terme de décalage à la sortie pondérée de la couche cachée et appliquons le sigmoïde. Pouvez-vous trouver les valeurs de h et b pour lesquelles vous obtenez une tour? Si vous êtes bloqué à ce stade, voici deux conseils: (1) pour que le neurone sortant démontre le comportement correct dans le style if-then-else, nous avons besoin que les poids entrants (tous h ou –h) soient grands; (2) la valeur de b détermine l'échelle du seuil si-alors-sinon.



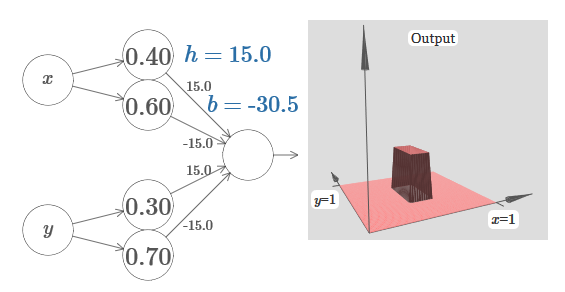
Avec les paramètres par défaut, la sortie est similaire à une version aplatie du diagramme précédent, avec une tour et un plateau. Pour obtenir le comportement souhaité, vous devez augmenter la valeur de h. Cela nous donnera le comportement de seuil de if-then-else. Deuxièmement, pour fixer correctement le seuil, il faut choisir b ≈ −3h / 2.

Voici à quoi cela ressemble pour h = 10:


Même pour des valeurs relativement modestes de h, nous obtenons une belle fonction de tour. Et, bien sûr, nous pouvons obtenir un résultat arbitrairement beau en augmentant encore h et en maintenant le biais au niveau b = −3h / 2.

Essayons de coller deux réseaux ensemble pour compter deux fonctions de tour différentes. Pour clarifier les rôles respectifs des deux sous-réseaux, je les mets dans des rectangles séparés: chacun d'eux calcule la fonction tour en utilisant la technique décrite ci-dessus. Le graphique de droite montre la sortie pondérée de la deuxième couche cachée, c'est-à-dire la combinaison pondérée des fonctions de la tour.



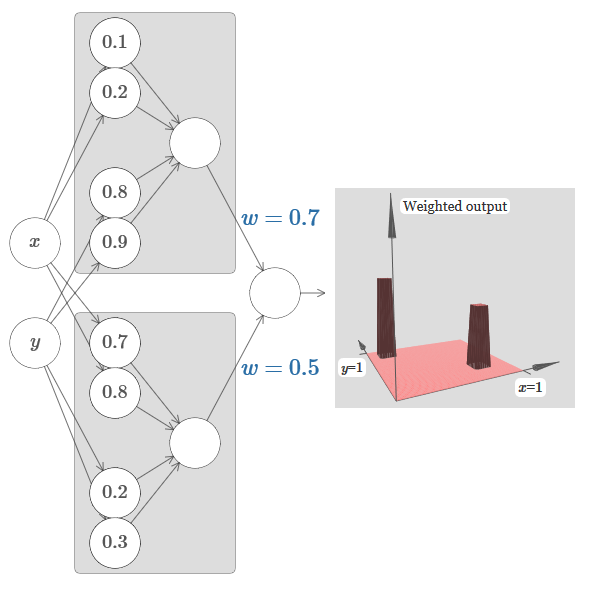
En particulier, on peut voir qu'en changeant le poids dans la dernière couche, vous pouvez changer la hauteur des tours de sortie.

La même idée vous permet de calculer autant de tours que vous le souhaitez. Nous pouvons les rendre arbitrairement minces et hauts. Par conséquent, nous garantissons que la sortie pondérée de la deuxième couche cachée se rapproche de toute fonction souhaitée de deux variables:



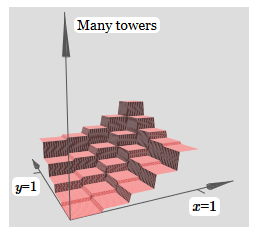
En particulier, en faisant bien approcher la sortie pondérée de la deuxième couche cachée σ ⁻¹ hiddenf, nous garantissons que la sortie de notre réseau sera une bonne approximation de la fonction f souhaitée.

Qu'en est-il des fonctions de nombreuses variables?

Essayons de prendre trois variables, x ₁ , x ₂ , x ₃ . Le réseau suivant peut-il être utilisé pour calculer la fonction de la tour en quatre dimensions?



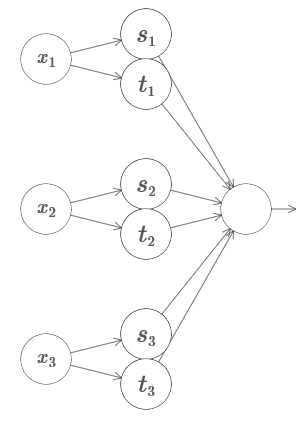
Ici x ₁ , x ₂ , x ₃ désignent l'entrée réseau. s ₁ , t _1, et ainsi de suite - les points de pas pour les neurones - c'est-à-dire que tous les poids dans la première couche sont grands, et les décalages sont assignés de sorte que les points de pas soient s ₁ , t ₁ , s ₂ , ... Les poids dans la deuxième couche alternent, + h, −h, où h est un très grand nombre. Le décalage de sortie est de -5h / 2.

Le réseau calcule une fonction égale à 1 dans trois conditions: x ₁ est compris entre s ₁ et t ₁ ; x ₂ est compris entre s ₂ et t ₂ ; x ₃ est compris entre s ₃ et t ₃ . Le réseau est 0 dans tous les autres endroits. Il s'agit d'une tour dans laquelle 1 est une petite partie de l'espace d'entrée et 0 est tout le reste.

En collant un grand nombre de ces réseaux, nous pouvons obtenir autant de tours que nous le souhaitons et approcher une fonction arbitraire de trois variables. La même idée fonctionne en m dimensions. Seul le décalage de sortie (−m + 1/2) h est modifié pour comprimer correctement les valeurs souhaitées et supprimer le plateau.

Eh bien, maintenant nous savons comment utiliser NS pour approximer la fonction réelle de nombreuses variables. Qu'en est-il des fonctions vectorielles f (x ₁ , ..., x _m ) ∈ R ⁿ ? Bien entendu, une telle fonction peut être considérée simplement comme n fonctions réelles distinctes f1 (x ₁ , ..., x _m ), f2 (x ₁ , ..., x _m ), etc. Et puis nous collons juste tous les réseaux ensemble. Il est donc facile de le comprendre.

Défi

• Nous avons vu comment utiliser des réseaux de neurones avec deux couches cachées pour approximer une fonction arbitraire. Pouvez-vous prouver que cela est possible avec une seule couche cachée? Astuce - essayez de travailler avec seulement deux variables de sortie et montrez que: (a) il est possible d'obtenir les fonctions des étapes non seulement le long des axes x ou y, mais aussi dans une direction arbitraire; (b) en additionnant de nombreuses constructions de l'étape (a), il est possible d'approcher la fonction d'une tour ronde plutôt que rectangulaire; © à l'aide de tours rondes, il est possible d'approximer une fonction arbitraire. L'étape © sera plus facile à réaliser en utilisant le matériel présenté dans ce chapitre un peu plus bas.

Aller au-delà des neurones sigmoïdes

Nous avons prouvé qu'un réseau de neurones sigmoïdes peut calculer n'importe quelle fonction. Rappelons que dans un neurone sigmoïde, les entrées x ₁ , x ₂ , ... se transforment à la sortie en σ (∑ _j w _j x _{j j} + b), où w _j sont les poids, b est le déplacement, σ est le sigmoïde.



Et si nous regardons un autre type de neurone utilisant une fonction d'activation différente, s (z):



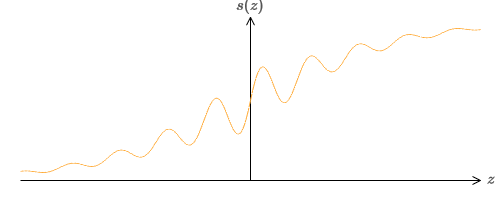
Autrement dit, nous supposons que si un neurone a x ₁ , x ₂ , ... les poids w ₁ , w ₂ , ... et le biais b à l'entrée, alors la sortie aura s ( _{j j} w _j x _{j j} + b).

On peut utiliser cette fonction d'activation pour se faire marcher, tout comme dans le cas du sigmoïde. Essayez (dans l' article d'origine ) sur le diagramme de soulever le poids pour, disons, w = 100:





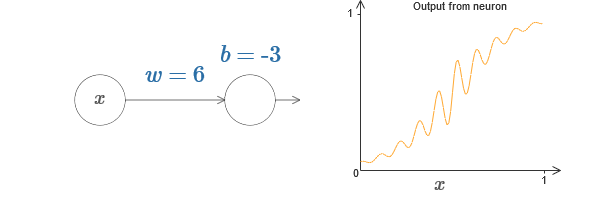
Comme dans le cas du sigmoïde, de ce fait, la fonction d'activation est compressée et, par conséquent, se transforme en une très bonne approximation de la fonction de pas. Essayez de changer le décalage, et vous verrez que nous pouvons changer l'emplacement de l'étape à n'importe quel. Par conséquent, nous pouvons utiliser toutes les mêmes astuces qu'auparavant pour calculer n'importe quelle fonction souhaitée.

Quelles propriétés doit avoir s (z) pour que cela fonctionne? Nous devons supposer que s (z) est bien défini comme z → −∞ et z → ∞. Ces limites sont deux valeurs acceptées par notre fonction pas à pas. Nous devons également supposer que ces limites sont différentes. S'ils ne différaient pas, les étapes ne fonctionneraient pas; il y aurait simplement un horaire fixe! Mais si la fonction d'activation s (z) satisfait à ces propriétés, les neurones basés sur celle-ci sont universellement adaptés aux calculs.

Les tâches

• Plus tôt dans le livre, nous avons rencontré un type différent de neurone - un neurone linéaire redressé ou une unité linéaire rectifiée, ReLU. Expliquez pourquoi ces neurones ne remplissent pas les conditions nécessaires à l'universalité. Trouvez des preuves de polyvalence montrant que les ReLU sont universellement adaptés à l'informatique.
• Supposons que nous considérons des neurones linéaires, avec la fonction d'activation s (z) = z. Expliquez pourquoi les neurones linéaires ne satisfont pas aux conditions d'universalité. Montrez que ces neurones ne peuvent pas être utilisés pour l'informatique universelle.

Fonction étape fixe

Pour le moment, nous avons supposé que nos neurones produisent des fonctions de pas précises. C'est une bonne approximation, mais seulement une approximation. En fait, il existe un étroit intervalle d'échec, illustré dans le graphique suivant, où les fonctions ne se comportent pas du tout comme une fonction pas à pas:



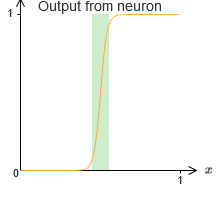
En cette période d'échec, mon explication de l'universalité ne fonctionne pas.

L'échec n'est pas si effrayant. En fixant des poids d'entrée suffisamment grands, nous pouvons rendre ces écarts arbitrairement petits. Nous pouvons les rendre beaucoup plus petits que sur la carte, invisibles à l'œil nu. Alors peut-être que nous n'avons pas à nous soucier de ce problème.

Néanmoins, j'aimerais avoir un moyen de le résoudre.

Il s'avère que c'est facile à résoudre. Voyons cette solution pour calculer les fonctions NS avec une seule entrée et une seule sortie. Les mêmes idées fonctionneront pour résoudre le problème avec un grand nombre d'entrées et de sorties.

Supposons en particulier que nous voulons que notre réseau calcule une fonction f. Comme précédemment, nous essayons de le faire en concevant le réseau de sorte que la sortie pondérée de la couche cachée de neurones soit σ ⁻¹ ⋅f (x):



Si nous le faisons en utilisant la technique décrite ci-dessus, nous forcerons les neurones cachés à produire une séquence de fonctions de protrusion:



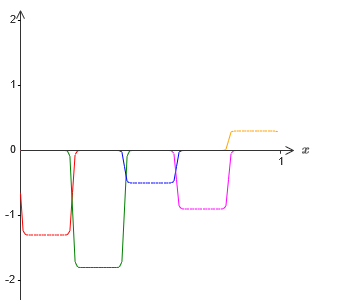
Bien sûr, j'ai exagéré la taille des intervalles d'échec, pour que ce soit plus facile à voir. Il devrait être clair que si nous additionnons toutes ces fonctions des protubérances, nous obtenons une assez bonne approximation de σ ⁻¹ ⋅f (x) partout sauf pour les intervalles de défaillance.

Mais, supposons qu'au lieu d'utiliser l'approximation qui vient d'être décrite, nous utilisons un ensemble de neurones cachés pour calculer l'approximation de la moitié de notre fonction objective d'origine, c'est-à-dire σ ⁻¹ ⋅f (x) / 2. Bien sûr, cela ressemblera à une version à l'échelle du dernier graphique:



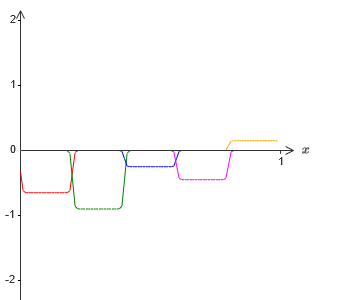
Et, supposons que nous faisons un autre ensemble de neurones cachés calculer l'approximation de σ ⁻¹ −f (x) / 2, cependant, à sa base, les protubérances seront décalées de la moitié de leur largeur:



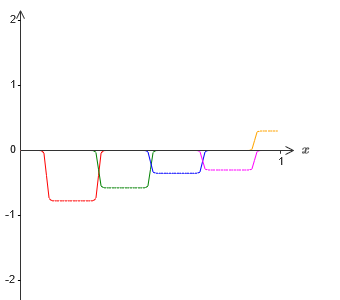
Nous avons maintenant deux approximations différentes pour σ - 1⋅f (x) / 2. Si nous additionnons ces deux approximations, nous obtenons une approximation générale de σ - 1⋅f (x). Cette approximation générale comportera toujours des inexactitudes à petits intervalles. Mais le problème sera moindre qu'auparavant - car les points tombant dans les intervalles de l'échec de la première approximation ne tomberont pas dans les intervalles de l'échec de la seconde approximation. Par conséquent, l'approximation de ces intervalles sera environ 2 fois meilleure.

Nous pouvons améliorer la situation en ajoutant un grand nombre, M, d'approximations qui se chevauchent de la fonction σ - 1⋅f (x) / M. Si tous leurs intervalles de défaillance sont suffisamment étroits, aucun courant ne sera dans l'un d'eux. Si vous utilisez un nombre suffisamment grand d'approximations de M qui se chevauchent, le résultat est une excellente approximation générale.

Conclusion

L'explication de l'universalité discutée ici ne peut certainement pas être appelée une description pratique de la façon de compter les fonctions à l'aide de réseaux de neurones! En ce sens, cela ressemble plus à une preuve de la polyvalence des portes logiques NAND et plus encore. Par conséquent, j'ai essentiellement essayé de rendre ce design clair et facile à suivre sans optimiser ses détails. Cependant, essayer d'optimiser cette conception peut être un exercice intéressant et instructif pour vous.

Bien que le résultat obtenu ne puisse pas être directement utilisé pour créer NS, il est important car il supprime la question de la calculabilité d'une fonction particulière utilisant NS. La réponse à une telle question sera toujours positive. Par conséquent, il est correct de demander si une fonction est calculable, mais quelle est la bonne façon de la calculer.

Notre conception universelle utilise seulement deux couches cachées pour calculer une fonction arbitraire. Comme nous l'avons vu, il est possible d'obtenir le même résultat avec une seule couche cachée. Compte tenu de cela, vous vous demandez peut-être pourquoi nous avons besoin de réseaux profonds, c'est-à-dire des réseaux avec un grand nombre de couches cachées. Ne pouvons-nous pas simplement remplacer ces réseaux par des réseaux peu profonds qui ont une couche cachée?

Bien que, en principe, cela soit possible, il existe de bonnes raisons pratiques d'utiliser des réseaux de neurones profonds. Comme décrit dans le chapitre 1, les NS profonds ont une structure hiérarchique qui leur permet de bien s'adapter pour étudier les connaissances hiérarchiques, qui sont utiles pour résoudre des problèmes réels. Plus précisément, lors de la résolution de problèmes tels que la reconnaissance de formes, il est utile d'utiliser un système qui comprend non seulement des pixels individuels, mais aussi des concepts de plus en plus complexes: des bordures aux formes géométriques simples, et au-delà, aux scènes complexes impliquant plusieurs objets. Dans les chapitres suivants, nous verrons des preuves en faveur du fait que les SN profonds seront mieux en mesure de faire face à l'étude de telles hiérarchies de connaissances que les NS peu profondes. Pour résumer: l'universalité nous dit que NS peut calculer n'importe quelle fonction; des données empiriques suggèrent que les NS profonds sont mieux adaptés à l'étude des fonctions utiles pour résoudre de nombreux problèmes du monde réel.