Une nouvelle méthode d'analyse des clusters est proposée. Son avantage réside dans un algorithme moins complexe en termes de calcul. La méthode est basée sur le calcul des votes pour le fait qu'une paire d'objets est dans la même classe à partir d'informations sur la valeur des coordonnées individuelles.
Présentation
Un grand besoin d'analyse des données est le développement de méthodes de classification efficaces. Dans de telles méthodes, il est nécessaire de diviser l'ensemble complet des objets en un nombre optimal de classes, basé uniquement sur des informations sur la valeur des indicateurs individuels [Zagoruyko 1999].
L'analyse en grappes est l'une des méthodes les plus populaires d'analyse de données et de statistiques mathématiques. L'analyse de cluster vous permet de trouver automatiquement des classes d'objets, en utilisant uniquement des informations sur les indicateurs quantitatifs des objets (formation sans professeur). Chacune de ces classes peut être définie par l'un de ses objets les plus caractéristiques, par exemple, la moyenne en termes d'indicateurs. Il existe un grand nombre de méthodes et d'approches pour classer les données.
Des recherches modernes dans le domaine de l'analyse des clusters sont menées pour améliorer les méthodes de détermination des classes de topologie complexe [Furaoa 2007, Zagoruiko 2013], ainsi que pour améliorer la vitesse des algorithmes dans le cas du big data.
Dans cet article, nous proposons une méthode de classification basée sur l'obtention de votes pour une paire d'objets dans la même classe, basée sur des informations sur la valeur des indicateurs individuels. Il est proposé de considérer qu'une paire d'objets est dans la même classe si les valeurs de leurs indicateurs individuels sont dans l'intervalle avec une longueur ne dépassant pas une valeur donnée.
Méthode K-means
La méthode k-means est l'une des méthodes de clustering les plus populaires. Son but est d'obtenir de tels centres de données qui correspondraient à l'hypothèse de compacité des classes de données avec leur distribution radiale symétrique. Une façon de déterminer la position de ces centres, étant donné leur nombre \ textit {k}, est l'approche EM.
Dans cette méthode, deux procédures sont effectuées séquentiellement.
- Définition pour chaque objet de données $ inline $ X_ {i} $ inline $ le centre le plus proche $ inline $ C_ {j} $ inline $ et attribuer une étiquette de classe à cet objet $ inline $ X_ {i} ^ {j} $ inline $ . De plus, pour tous les objets, leur appartenance à différentes classes devient déterminée.
- Calcul de la nouvelle position des centres de toutes les classes.
En répétant itérativement ces deux procédures à partir de la position aléatoire initiale des centres des classes \ textit {k}, nous pouvons réaliser la séparation des objets en classes qui correspondraient le mieux à l'hypothèse de compacité radiale des classes.
Un nouvel algorithme de classification de l'auteur sera comparé à la méthode k-means.
Nouvelle méthode
Le nouvel algorithme d'analyse des clusters est construit sur la base des votes d'appartenance à différents clusters à partir d'informations sur les valeurs des coordonnées individuelles des points de données.
- Une valeur d est spécifiée qui caractérise la longueur de l'intervalle d'indicateurs au sein duquel deux objets sont considérés comme appartenant à la même classe.
- Métrique sélectionnée $ inline $ x_ {i} $ inline $ et toutes les paires d'objets sont considérées $ inline $ \ left \ {O_ {l}, O_ {k} \ right \} $ inline $ où $ inline $ l, k = 1 \ ldots N $ inline $ .
- Si $ inline $ \ left | x_ {i} ^ {l} -x_ {i} ^ {k} \ right | \ le d $ inline $ puis l'ampleur $ inline $ r_ {lk}: = r_ {lk} + 1 $ inline $ (voix ajoutée).
- Les actions 2) et 3) sont répétées pour tous les indicateurs $ inline $ i = 1 \ ldots M $ inline $ .
- La valeur p caractérisant le nombre minimum de votes pour l'appartenance aux mêmes classes est fixée.
- En utilisant la méthode des paires de valeurs clés, toutes les classes d'objets sont déterminées, de telle sorte qu'au sein d'une classe de voix pour les paires d'objets de ces classes > = p .
- Répète toutes les valeurs de d et p et répète les points 1) - 6) pour obtenir le nombre de classes le plus proche du nombre donné de classes g .
Pour réduire la complexité de l'algorithme à
N , vous pouvez utiliser
des intervalles
T pour des indicateurs individuels et remplacer les clauses 2) et 3) dans l'algorithme par ce qui suit:
1. L'indicateur est sélectionné
$ inline $ x_ {i} $ inline $ et tous les intervalles sont considérés
$ inline $ \ left [u_ {l}, w_ {l} \ right] $ inline $ où
$ inline $ l = 1 \ ldots T $ inline $ :
$$ afficher $$ u_ {0} = \ min (x_ {i}); u_ {0} = \ min (x_ {i}); $$ afficher $$
$$ afficher $$ w_ {T} = \ max (x_ {i}); $$ afficher $$
$$ afficher $$ s_ {i} = w_ {T} -u_ {0}; $$ afficher $$
$$ afficher $$ u_ {l} = u_ {0} + l \ cdot s_ {i}; $$ afficher $$
$$ afficher $$ w_ {l} = u_ {l} + d; $$ afficher $$
2. Si
$ inline $ x_ {i} ^ {k} \ in \ left [u_ {j}, w_ {j} \ right] $ inline $ et
$ inline $ x_ {i} ^ {l} \ in \ left [u_ {j}, w_ {j} \ right] $ inline $ où
$ inline $ j = 1 \ ldots T $ inline $ puis l'ampleur
$ inline $ r_ {lk}: = r_ {lk} + 1 $ inline $ (la voix est ajoutée avec une touche unique
l ,
k pour le
i- ème indicateur).
Expérience numérique
Les données avec la classification intuitive pour l'homme ont été prises comme données initiales.
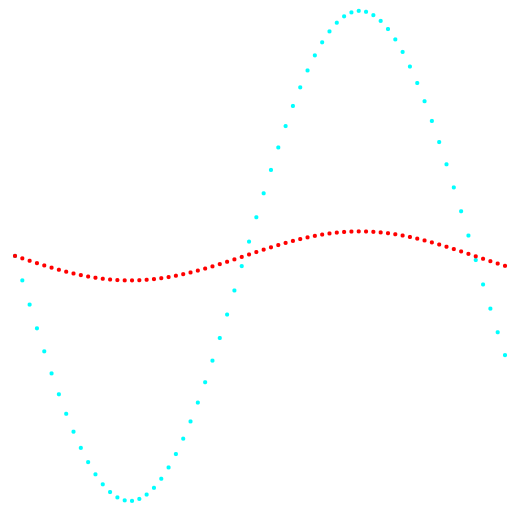
Les figures 1 et 2 montrent les résultats de la classification de la méthode des k-moyennes et de la nouvelle méthode de classification.
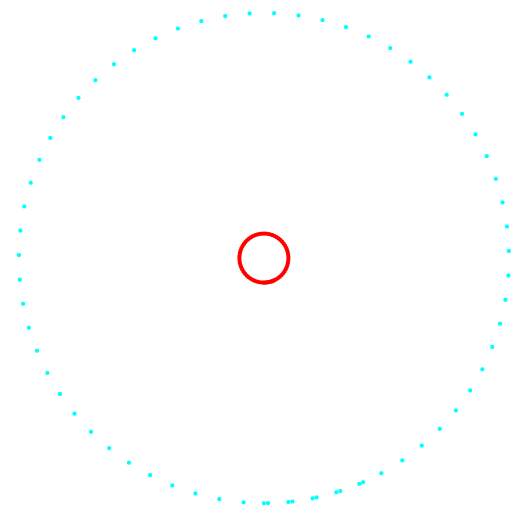Fig. 1. Projection 1-2 et classification des données.À gauche, la méthode k-means, à droite, la méthode de l'auteur.
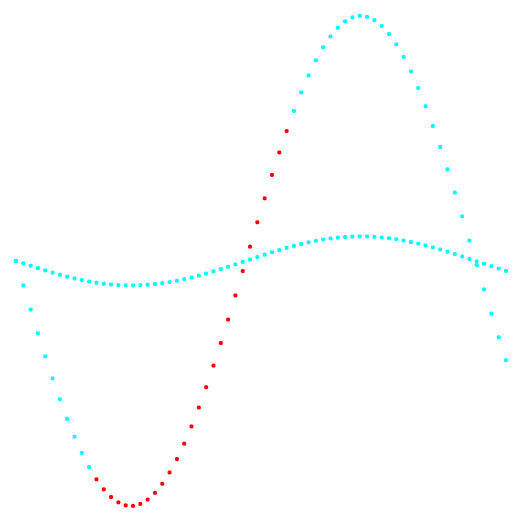
Fig. 2. Projection 2-3 et classification des données.À gauche, la méthode k-means, à droite, la méthode de l'auteur.
Le résultat de la comparaison des deux méthodes montre l'avantage évident de la méthode de l'auteur dans sa capacité à détecter des clusters de topologie complexe.
Implémentation logicielle
La méthode de clustering k-means a été implémentée par programme en tant qu'application Web. La partie informatique de l'application est soumise à un serveur écrit en PHP utilisant le framework Zend. L'interface de l'application est écrite en utilisant HTML, CSS, JavaScript, jQuery. L'application est disponible sur
http://svlaboratory.org/application/klaster2 après l'enregistrement d'un nouvel utilisateur. L'application vous permet de visualiser l'appartenance d'objets à différents clusters dans un plan de coordonnées donné.
Conclusion
Une nouvelle méthode de classification est proposée. Les avantages de cette méthode sont la reconnaissance de classes de topologie complexe, la distribution non radiale, ainsi que la complexité moindre de l'algorithme et moins d'actions, ce qui est particulièrement bénéfique dans le cas de grands tableaux de données.
Les références- Zagoruyko N.G. Méthodes appliquées d'analyse des données et des connaissances. Novossibirsk: maison d'édition de l'Institut de mathématiques, 1999.270 p.
- Zagoruyko N.G., Borisova I.A., Kutnenko O.A., Levanov D.A. Détection de modèles dans des matrices de données expérimentales // Technologies informatiques. - 2013, vol. 18. n ° S1. S. 12-20.
- Shen Furaoa, Tomotaka Ogurab, Osamu Hasegawab Un réseau neuronal incrémental auto-organisé amélioré pour l'apprentissage non supervisé en ligne. Laboratoire Hasegawa, 2007.