La traduction a été préparée pour les étudiants du cours «Applied Analytics on R» .
C'était ma première tentative de regrouper des clients sur la base de données réelles, et cela m'a donné une expérience précieuse. Il existe de nombreux articles sur Internet sur le regroupement à l'aide de variables numériques, mais trouver des solutions pour les données catégorielles, qui est un peu plus difficile, n'était pas si simple. Les méthodes de regroupement des données catégorielles sont toujours en cours de développement, et dans un autre article, je vais en essayer un autre.
D'un autre côté, de nombreuses personnes pensent que le regroupement de données catégorielles peut ne pas produire de résultats significatifs - et cela est en partie vrai (voir l'
excellente discussion sur CrossValidated ). À un moment donné, j'ai pensé: «Qu'est-ce que je fais? Ils peuvent simplement être divisés en cohortes. » Cependant, l'analyse de cohorte n'est également pas toujours recommandée, en particulier avec un nombre significatif de variables catégorielles avec un grand nombre de niveaux: vous pouvez facilement traiter 5-7 cohortes, mais si vous avez 22 variables et chacune a 5 niveaux (par exemple, une enquête client avec des estimations discrètes 1 , 2, 3, 4 et 5), et vous devez comprendre à quels groupes de clients caractéristiques vous avez affaire - vous obtiendrez des cohortes de 22x5. Personne ne veut s'embêter avec une telle tâche. Et ici, le clustering pourrait aider. Donc, dans cet article, je parlerai de ce que j'aimerais savoir moi-même dès que j'ai commencé à regrouper.
Le processus de clustering lui-même comprend trois étapes:
- Construire une matrice de dissimilarité est sans aucun doute la décision la plus importante dans le clustering. Toutes les étapes suivantes seront basées sur la matrice de dissimilarité que vous avez créée.
- Le choix de la méthode de clustering.
- Évaluation des grappes.
Ce billet sera une sorte d'introduction qui décrit les principes de base du clustering et sa mise en œuvre dans l'environnement R.
Matrice de dissimilarité
La base du clustering sera la matrice de dissimilarité qui, en termes mathématiques, décrit la différence (supprimée) entre les points de l'ensemble de données. Il vous permet de combiner davantage dans les groupes les points les plus proches les uns des autres, ou de séparer les plus éloignés les uns des autres - c'est l'idée principale du clustering.
À ce stade, les différences entre les types de données sont importantes, car la matrice de dissimilarité est basée sur les distances entre les points de données individuels. Il est facile d'imaginer les distances entre les points de données numériques (un exemple bien connu est
les distances euclidiennes ), mais dans le cas de données catégorielles (facteurs en R), tout n'est pas si évident.
Afin de construire une matrice de dissimilarité dans ce cas, la distance dite de Gover doit être utilisée. Je ne m'attarderai pas sur la partie mathématique de ce concept, je fournirai simplement des liens:
ici et
là . Pour cela, je préfère utiliser
daisy() avec la
metric = c("gower") du package de
cluster .
La matrice de dissimilarité est prête. Pour 200 observations, il est construit rapidement, mais peut nécessiter une très grande quantité de calcul si vous avez affaire à un grand ensemble de données.
Dans la pratique, il est très probable que vous deviez d'abord nettoyer l'ensemble de données, effectuer les transformations nécessaires des lignes en facteurs et suivre les valeurs manquantes. Dans mon cas, l'ensemble de données contenait également des lignes de valeurs manquantes qui étaient joliment regroupées à chaque fois, il semblait donc que c'était un trésor - jusqu'à ce que je regarde les valeurs (hélas!).
Algorithmes de clustering
Vous savez peut-être déjà que le clustering est
k-means et hiérarchique . Dans cet article, je me concentre sur la deuxième méthode, car elle est plus flexible et permet différentes approches: vous pouvez choisir un algorithme de clustering
agglomératif (de bas en haut) ou
divisionnaire (de haut en bas).
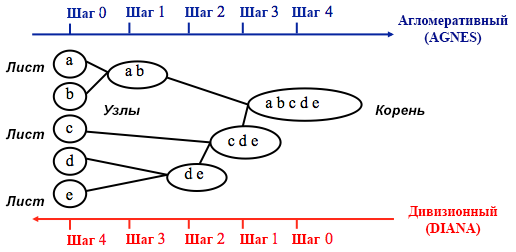Source: Guide de programmation UC Business Analytics RLe clustering agglomératif commence par
n clusters, où
n est le nombre d'observations: on suppose que chacun d'eux est un cluster séparé. Ensuite, l'algorithme essaie de trouver et de regrouper les points de données les plus similaires entre eux - c'est ainsi que la formation des clusters commence.
Le regroupement divisionnaire est effectué de la manière opposée - il est initialement supposé que tous les n points de données que nous avons sont un grand cluster, puis les moins similaires sont divisés en groupes séparés.
Lorsque vous décidez laquelle de ces méthodes choisir, il est toujours judicieux d'essayer toutes les options.Cependant, en général, le
clustering aggloméré est meilleur pour identifier les petits clusters et est utilisé par la plupart des programmes informatiques, et le clustering divisionnaire est plus approprié pour identifier les grands clusters .
Personnellement, avant de décider quelle méthode utiliser, je préfère regarder les dendrogrammes - une représentation graphique du clustering. Comme vous le verrez plus tard, certains dendrogrammes sont bien équilibrés, tandis que d'autres sont très chaotiques.
# L'entrée principale pour le code ci-dessous est la dissimilarité (matrice de distance)
Évaluation de la qualité du clustering
A ce stade, il est nécessaire de choisir entre différents algorithmes de clustering et un nombre différent de clusters. Vous pouvez utiliser différentes méthodes d'évaluation, sans oublier de vous laisser guider par le
bon sens . J'ai souligné ces mots en gras et en italique, car la signification du choix est
très importante - le nombre de grappes et la méthode de division des données en groupes doivent être pratiques d'un point de vue pratique. Le nombre de combinaisons de valeurs de variables catégorielles est fini (car elles sont discrètes), mais aucune ventilation basée sur elles ne sera significative. Vous pouvez également ne pas vouloir avoir très peu de clusters - dans ce cas, ils seront trop généralisés. En fin de compte, tout dépend de votre objectif et des tâches de l'analyse.
En général, lors de la création de clusters, vous souhaitez obtenir des groupes de points de données clairement définis, de sorte que la distance entre ces points au sein du cluster (
ou compacité ) soit minimale, et la distance entre les groupes (
séparabilité ) soit le maximum possible. Ceci est facile à comprendre intuitivement: la distance entre les points est une mesure de leur dissimilarité, obtenue à partir de la matrice de dissimilarité. Ainsi, l'évaluation de la qualité du clustering est basée sur l'évaluation de la compacité et de la séparabilité.
Ensuite, je vais démontrer deux approches et montrer que l'une d'elles peut donner des résultats dénués de sens.
- Méthode du coude : commencez par celle-ci si le facteur le plus important pour votre analyse est la compacité des grappes, c'est-à-dire la similitude au sein des groupes.
- Méthode d'évaluation des silhouettes : Le graphique de silhouette utilisé comme mesure de la cohérence des données montre à quel point chacun des points d'un cluster est proche des points des clusters voisins.
Dans la pratique, ces deux méthodes donnent souvent des résultats différents, ce qui peut entraîner une certaine confusion - la compacité maximale et la séparation la plus claire seront obtenues avec un nombre différent de clusters, de sorte que le bon sens et la compréhension de ce que vos données signifient réellement joueront un rôle important lors de la prise de décision finale.
Il existe également un certain nombre de mesures que vous pouvez analyser. Je vais les ajouter directement au code.
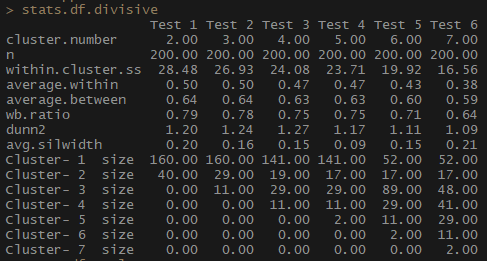
Ainsi, l'indicateur average .within, qui représente la distance moyenne entre les observations au sein des grappes, diminue, de même que within.cluster.ss (la somme des carrés des distances entre les observations dans une grappe). La largeur moyenne de la silhouette (largeur moyenne) ne change pas sans ambiguïté, cependant, une relation inverse peut encore être remarquée.
Remarquez à quel point les tailles de cluster sont disproportionnées. Je ne me précipiterais pas pour travailler avec un nombre incomparable d'observations au sein des clusters. L'une des raisons est que l'ensemble de données peut être déséquilibré, et certains groupes d'observations l'emporteront sur tous les autres dans l'analyse - ce n'est pas bon et conduira très probablement à des erreurs.
stats.df.aggl <-cstats.table(gower.dist, aggl.clust.c, 7) #stats.df.aggl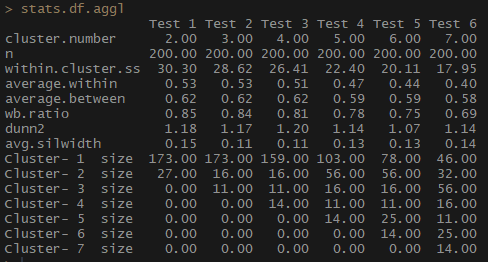
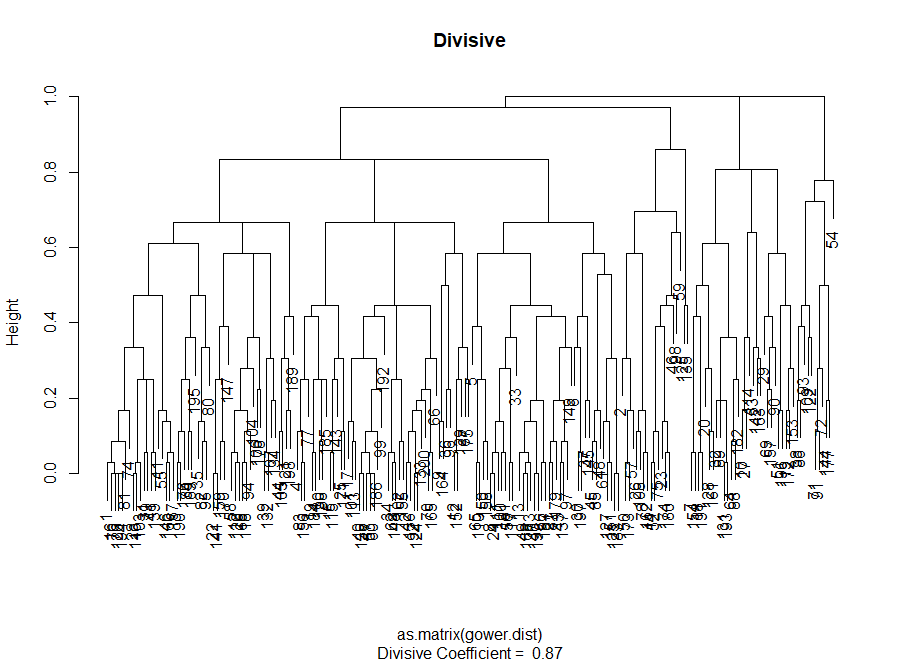
Remarquez à quel point le nombre d'observations par groupe est mieux équilibré par le regroupement hiérarchique aggloméré basé sur la méthode de communication complète.
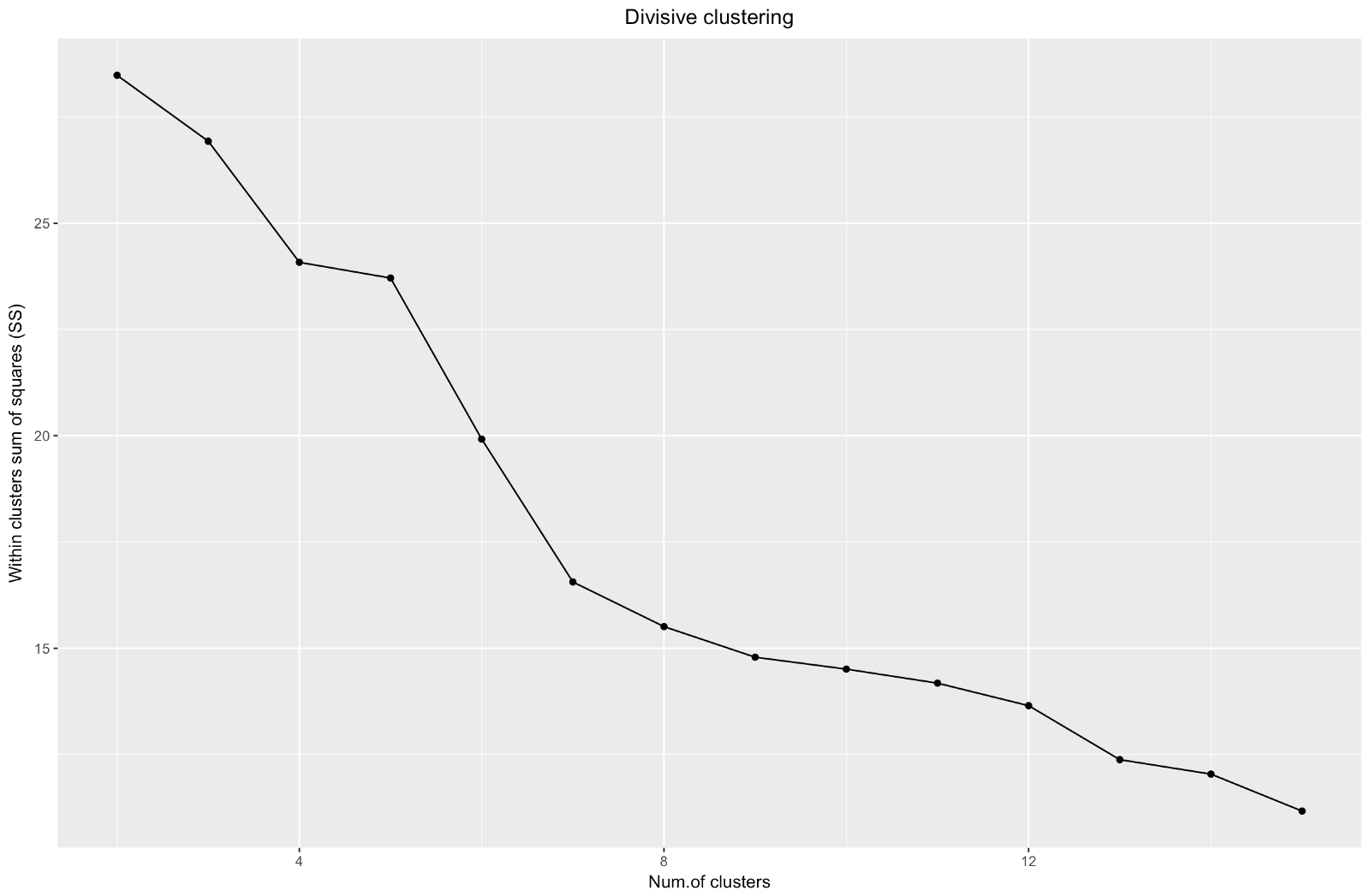
Nous avons donc créé un graphique du «coude». Il montre comment la somme des distances au carré entre les observations (nous l'utilisons comme mesure de la proximité des observations - plus elle est petite, plus les mesures à l'intérieur du cluster sont proches les unes des autres) varie pour un nombre différent de clusters. Idéalement, nous devrions voir un «coude de coude» distinct au point où un regroupement supplémentaire ne donne qu'une légère diminution de la somme des carrés (SS). Pour le graphique ci-dessous, je m'arrêterais à environ 7. Bien que dans ce cas l'un des clusters ne comprendra que deux observations. Voyons ce qui se passe lors du clustering agglomératif.
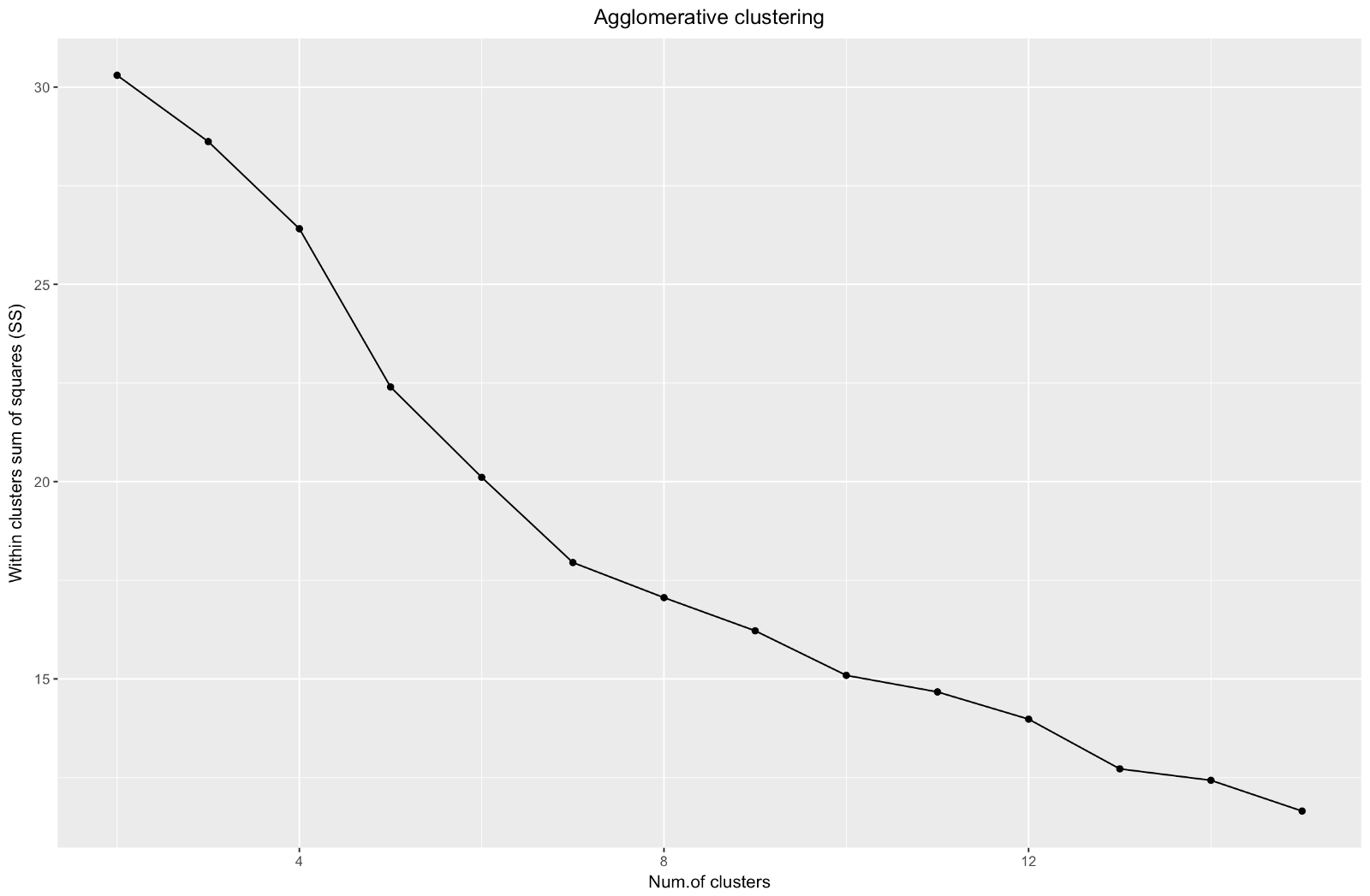
Le «coude» aggloméré est similaire à la division, mais le graphique semble plus lisse - les courbes ne sont pas si prononcées. Comme pour le clustering divisionnaire, je me concentrerais sur 7 clusters, cependant, lorsque je choisis entre ces deux méthodes, j'aime davantage les tailles de cluster obtenues par la méthode agglomérative - il vaut mieux qu'elles soient comparables.
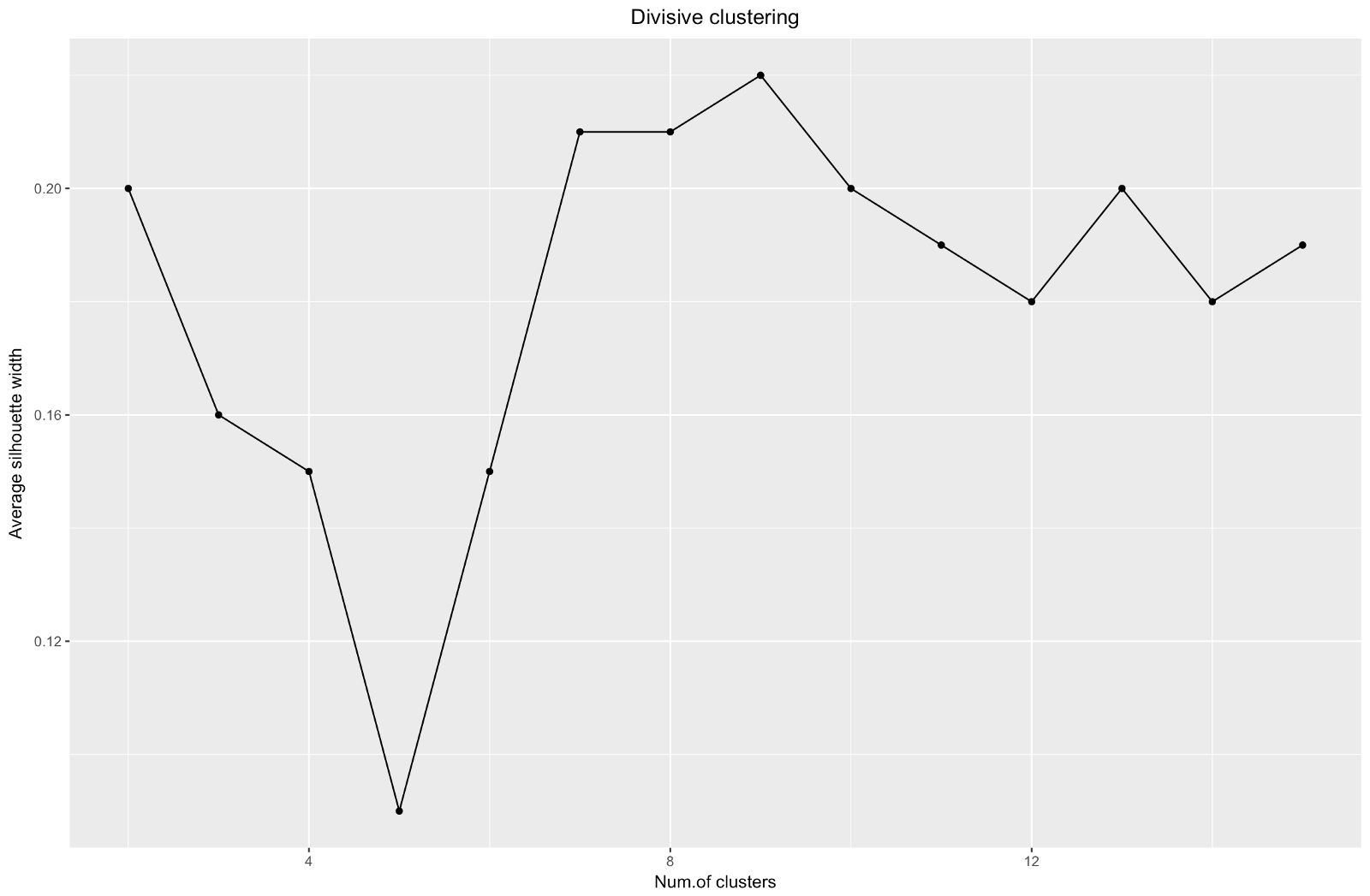
Lorsque vous utilisez la méthode d'estimation de la silhouette, vous devez choisir la quantité qui donne le coefficient de silhouette maximal, car vous avez besoin de grappes suffisamment éloignées pour être considérées comme distinctes.
Le coefficient de silhouette peut aller de –1 à 1, 1 correspondant à une bonne cohérence au sein des grappes et –1 pas très bon.
Dans le cas du graphique ci-dessus, vous choisiriez 9 plutôt que 5 grappes.
A titre de comparaison: dans le cas «simple», le graphique de silhouette est similaire à celui ci-dessous. Pas tout à fait comme le nôtre, mais presque.
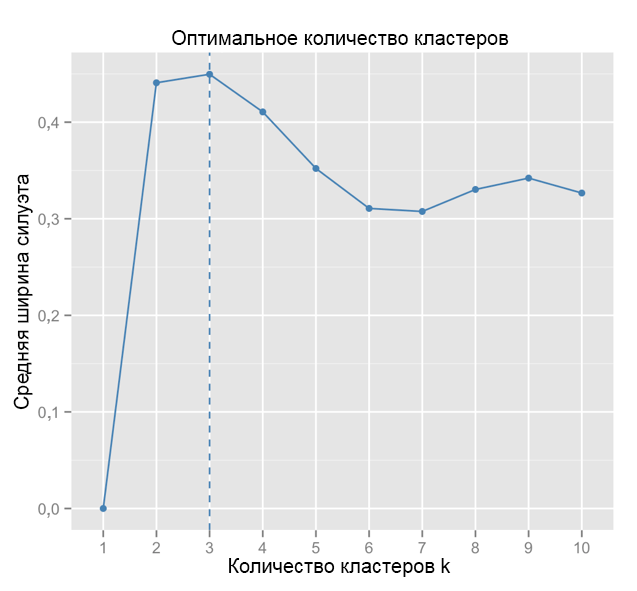Source: Data Sailors ggplot(data = data.frame(t(cstats.table(gower.dist, aggl.clust.c, 15))), aes(x=cluster.number, y=avg.silwidth)) + geom_point()+ geom_line()+ ggtitle("Agglomerative clustering") + labs(x = "Num.of clusters", y = "Average silhouette width") + theme(plot.title = element_text(hjust = 0.5))
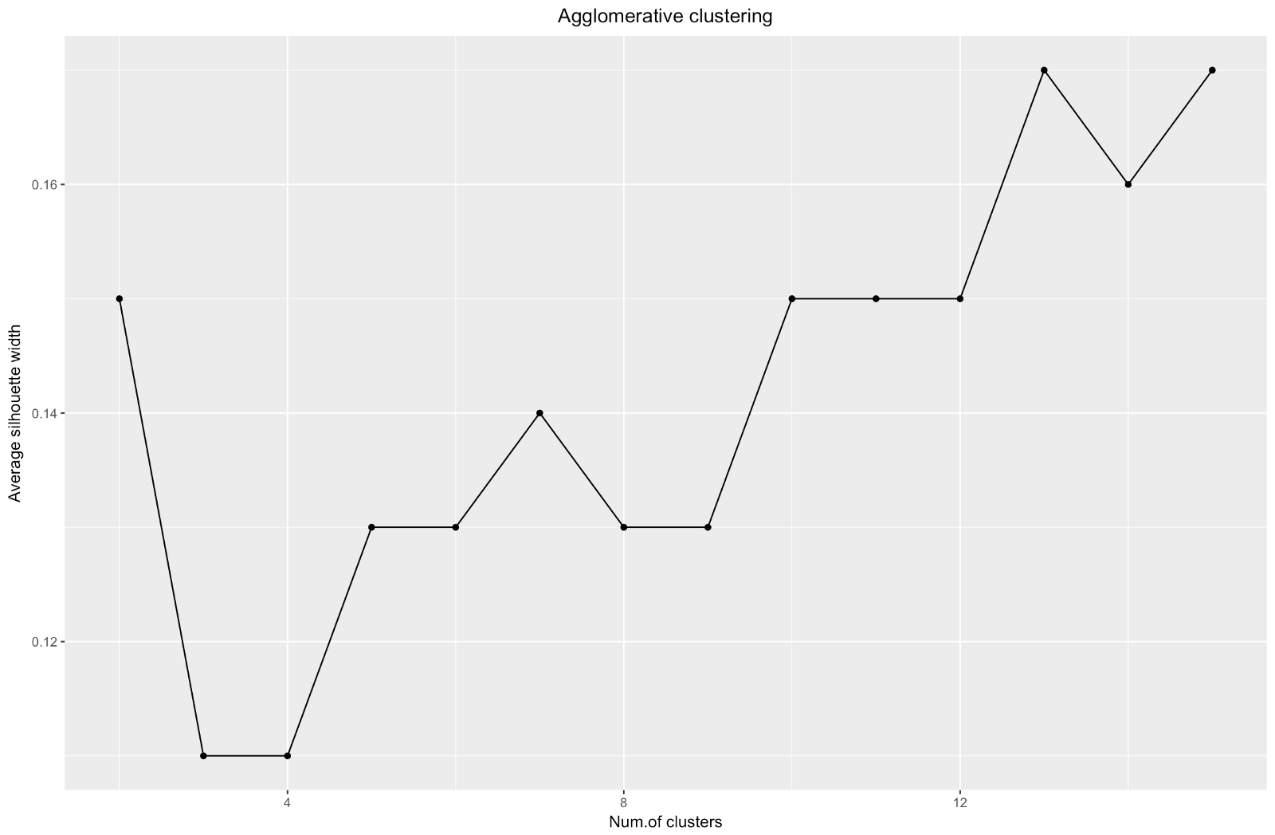
Le graphique de largeur de silhouette nous dit: plus vous divisez l'ensemble de données, plus les clusters deviennent clairs. Cependant, à la fin, vous atteindrez des points individuels et vous n'en aurez pas besoin. Cependant, c'est exactement ce que vous verrez si vous commencez à augmenter le nombre de clusters
k . Par exemple, pour
k=30 j'ai obtenu le graphique suivant:
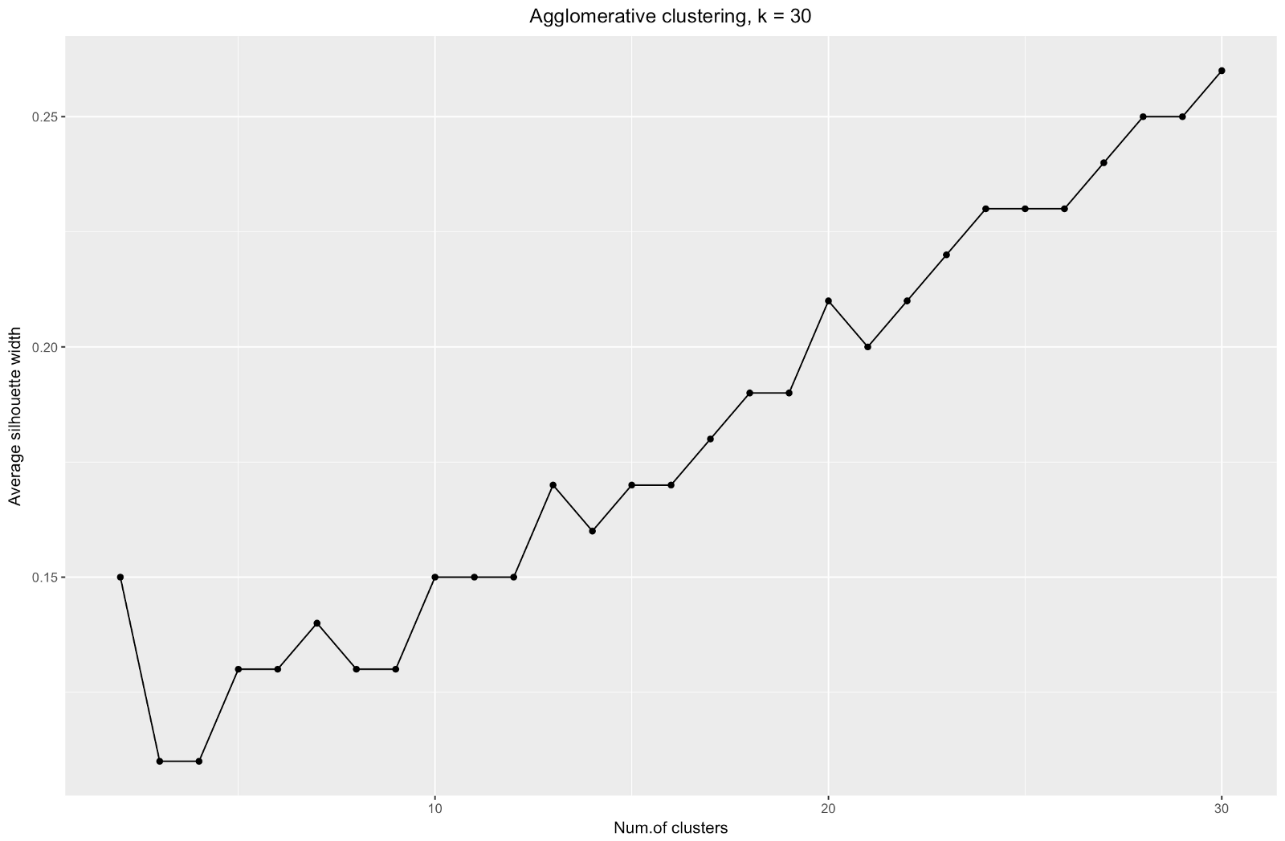
Pour résumer: plus vous divisez l'ensemble de données, meilleurs sont les clusters, mais nous ne pouvons pas atteindre des points individuels (par exemple, dans le graphique ci-dessus, nous avons sélectionné 30 clusters et nous n'avons que 200 points de données).
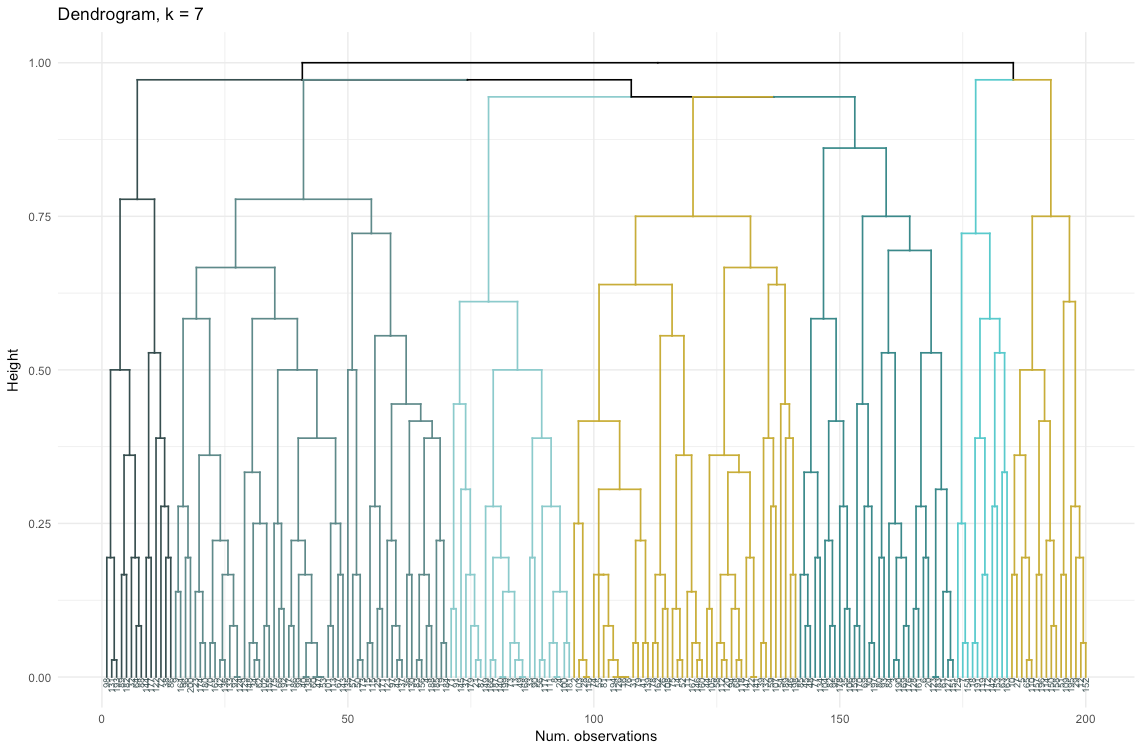
Ainsi, le clustering aggloméré dans notre cas me semble beaucoup plus équilibré: les tailles de cluster sont plus ou moins comparables (il suffit de regarder un cluster de seulement deux observations lors de la division par la méthode divisionnaire!), Et je m'arrêterais à 7 clusters obtenus par cette méthode. Voyons à quoi ils ressemblent et de quoi ils sont faits.
L'ensemble de données se compose de 6 variables qui doivent être visualisées en 2D ou 3D, vous devez donc travailler dur! La nature des données catégorielles impose également certaines limites, de sorte que les solutions toutes faites peuvent ne pas fonctionner. Je dois: a) voir comment les observations sont divisées en grappes, b) comprendre comment les observations sont classées. Par conséquent, j'ai créé a) un dendrogramme en couleurs, b) une carte thermique du nombre d'observations par variable à l'intérieur de chaque groupe.
library("ggplot2") library("reshape2") library("purrr") library("dplyr")
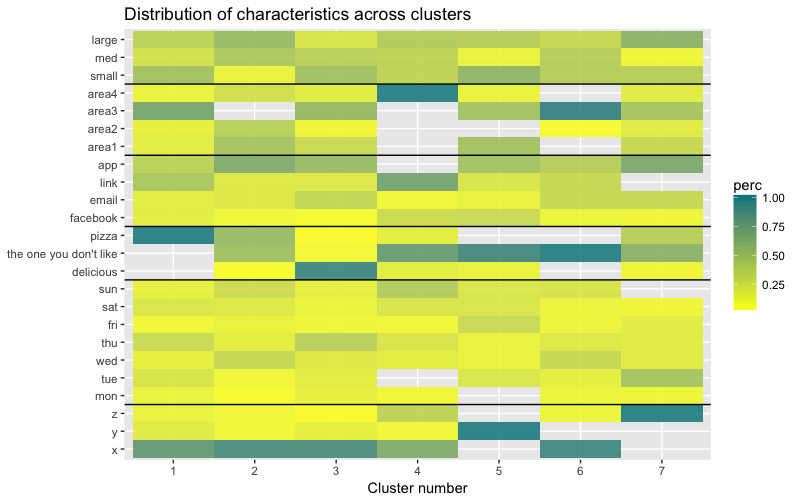
La carte thermique montre graphiquement combien d'observations sont faites pour chaque niveau de facteur pour les facteurs initiaux (les variables avec lesquelles nous avons commencé). La couleur bleu foncé correspond à un nombre relativement important d'observations au sein de l'amas. Cette carte de chaleur montre également que pour le jour de la semaine (soleil, sam ... lun) et la taille du panier (grand, moyen, petit), le nombre de clients dans chaque cellule est presque le même - cela peut signifier que ces catégories ne sont pas déterminantes pour l'analyse, et Il n'est peut-être pas nécessaire d'en tenir compte.
Conclusion
Dans cet article, nous avons calculé la matrice de dissimilarité, testé les méthodes d'agglomération et de division du clustering hiérarchique et nous sommes familiarisés avec les méthodes du coude et de la silhouette pour évaluer la qualité des clusters.
Le clustering hiérarchique divisionnaire et aggloméré est un bon début pour étudier le sujet, mais ne vous arrêtez pas là si vous voulez vraiment maîtriser l'analyse de cluster. Il existe de nombreuses autres méthodes et techniques. La principale différence avec le regroupement des données numériques est le calcul de la matrice de dissimilarité. Lors de l'évaluation de la qualité du regroupement, toutes les méthodes standard ne donneront pas des résultats fiables et significatifs - la méthode de la silhouette n'est probablement pas appropriée.
Et enfin, comme un certain temps s'est déjà écoulé depuis que j'ai fait cet exemple, je vois maintenant un certain nombre de lacunes dans mon approche et je serai heureux de tout commentaire. L'un des problèmes importants de mon analyse n'était pas lié au clustering en tant que tel -
mon ensemble de données était déséquilibré à bien des égards, et ce moment restait inexpliqué. Cela a eu un effet notable sur le regroupement: 70% des clients appartenaient à un niveau du facteur «citoyenneté» et ce groupe dominait la plupart des grappes obtenues, il était donc difficile de calculer les différences entre les autres niveaux du facteur. La prochaine fois, j'essaierai d'équilibrer l'ensemble de données et de comparer les résultats du clustering. Mais plus à ce sujet dans un autre post.
Enfin, si vous souhaitez cloner mon code, voici le lien vers github:
https://github.com/khunreus/cluster-categoricalJ'espère que cet article vous a plu!
Sources qui m'ont aidé:
Guide de clustering hiérarchique (préparation des données, clustering, visualisation) - ce blog sera intéressant pour ceux qui sont intéressés par l'analyse commerciale dans l'environnement R:
http://uc-r.imtqy.com/hc_clustering et
https: // uc-r. imtqy.com/kmeans_clusteringClustering:
http://www.sthda.com/english/articles/29-cluster-validation-essentials/97-cluster-validation-statistics-must-know-methods/( k-):
https://eight2late.wordpress.com/2015/07/22/a-gentle-introduction-to-cluster-analysis-using-r/denextend, :
https://cran.r-project.org/web/packages/dendextend/vignettes/introduction.html#the-set-function, :
https://www.r-statistics.com/2010/06/clustergram-visualization-and-diagnostics-for-cluster-analysis-r-code/:
https://jcoliver.imtqy.com/learn-r/008-ggplot-dendrograms-and-heatmaps.html,
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5025633/ ( GitHub:
https://github.com/khunreus/EnsCat ).