Réseaux de neurones et apprentissage profond, chapitre 5: pourquoi les réseaux de neurones profonds sont-ils si difficiles à former?

Imaginez que vous êtes ingénieur et qu'on vous a demandé de développer un ordinateur à partir de zéro. Une fois que vous êtes assis au bureau, concevez des circuits logiques de toutes vos forces, distribuez des vannes ET, OU, etc., et soudain, votre patron entre et vous annonce la mauvaise nouvelle. Le client vient de décider d'ajouter une exigence inattendue au projet: le schéma de l'ensemble de l'ordinateur ne doit pas comporter plus de deux couches:



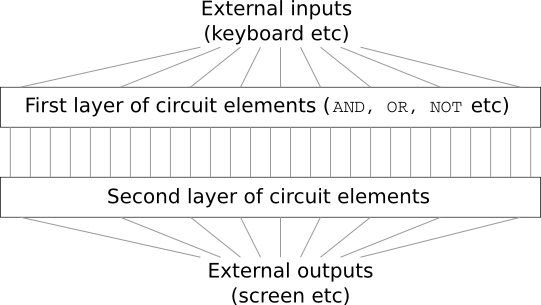
Vous êtes étonné et dites au patron: "Oui, le client est fou!"

Le patron répond: «Je le pense aussi. Mais le client doit obtenir ce qu'il veut. "

En fait, au sens étroit, le client n'est pas complètement fou. Supposons que vous êtes autorisé à utiliser une porte logique spéciale qui vous permet de connecter n'importe quel nombre d'entrées via AND. Et vous êtes autorisé à utiliser la porte NAND avec n'importe quel nombre d'entrées, c'est-à-dire une telle porte qui additionne beaucoup d'entrées via AND, puis inverse le résultat. Il s'avère qu'avec de telles vannes spéciales, vous pouvez calculer n'importe quelle fonction avec juste un circuit à deux couches.

Cependant, ce n'est pas parce que quelque chose peut être fait que cela en vaut la peine. En pratique, lors de la résolution de problèmes liés à la conception de circuits logiques (et de presque tous les problèmes algorithmiques), nous commençons généralement par résoudre des sous-problèmes, puis assemblons progressivement une solution complète. En d'autres termes, nous construisons une solution à travers de nombreux niveaux d'abstraction.

Par exemple, supposons que nous concevions un circuit logique pour multiplier deux nombres. Il est probable que nous souhaitons le construire à partir de sous-circuits qui implémentent des opérations telles que l'ajout de deux nombres. Les sous-circuits d'addition, à leur tour, seront constitués de sous-circuits ajoutant deux bits. En gros, notre schéma ressemblera à ceci:



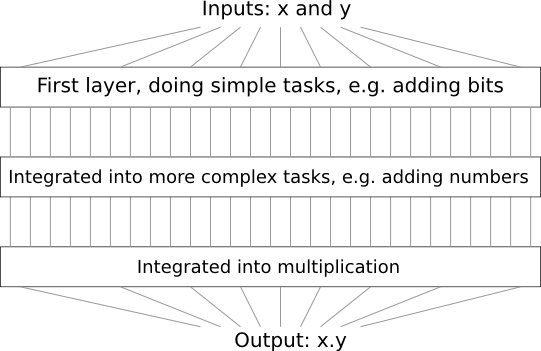
C'est-à-dire que le dernier circuit contient au moins trois couches d'éléments de circuit. En fait, il y aura probablement plus de trois couches lorsque nous diviserons les sous-tâches en plus petites que celles que j'ai décrites. Mais vous avez compris le principe.

Par conséquent, les schémas profonds facilitent le processus de conception. Mais ils aident non seulement à la conception. Il existe des preuves mathématiques que pour calculer certaines fonctions dans des circuits très peu profonds, il est nécessaire d'utiliser un nombre exponentiellement plus élevé d'éléments que dans des éléments profonds. Par exemple, il existe une célèbre série d'ouvrages scientifiques des années 1980, où il a été démontré que le calcul de la parité d'un ensemble de bits nécessite un nombre exponentiellement plus grand de portes avec un circuit peu profond. En revanche, lorsque vous utilisez des schémas profonds, il est plus facile de calculer la parité à l'aide d'un petit schéma: vous calculez simplement la parité des paires de bits, puis utilisez le résultat pour calculer la parité des paires de bits, etc., pour atteindre rapidement la parité générale. Par conséquent, les schémas profonds peuvent être beaucoup plus puissants que ceux peu profonds.

Jusqu'à présent, ce livre a utilisé une approche des réseaux de neurones (NS), similaire aux demandes d'un client fou. Presque tous les réseaux avec lesquels nous avons travaillé avaient une seule couche cachée de neurones (plus les couches d'entrée et de sortie):



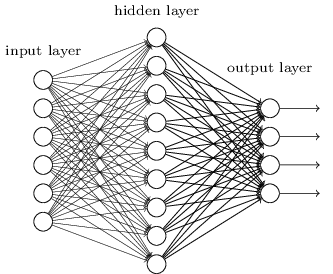
Ces réseaux simples se sont avérés très utiles: dans les chapitres précédents, nous avons utilisé ces réseaux pour classer les nombres manuscrits avec une précision supérieure à 98%! Cependant, il est intuitivement clair que les réseaux avec de nombreuses couches cachées seront beaucoup plus puissants:



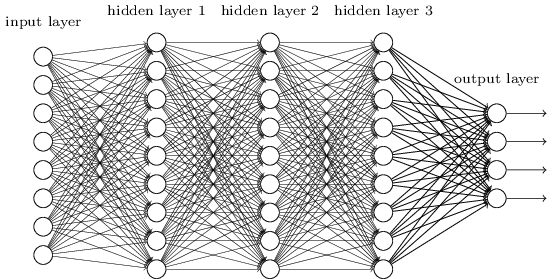
Ces réseaux peuvent utiliser des couches intermédiaires pour créer de nombreux niveaux d'abstraction, comme c'est le cas avec nos schémas booléens. Par exemple, dans le cas de la reconnaissance de formes, les neurones de la première couche peuvent apprendre à reconnaître les visages, les neurones de la deuxième couche - des formes plus complexes, par exemple des triangles ou des rectangles créés à partir de visages. La troisième couche pourra alors reconnaître des formes encore plus complexes. Et ainsi de suite. Il est probable que ces nombreuses couches d'abstraction donneront aux réseaux profonds un avantage convaincant pour résoudre les problèmes de reconnaissance de motifs complexes. De plus, comme dans le cas des circuits, des résultats théoriques confirment que les réseaux profonds ont intrinsèquement plus de capacités que les réseaux peu profonds.

Comment formons-nous ces réseaux de neurones profonds (GNS)? Dans ce chapitre, nous allons essayer de former STS en utilisant notre cheval de bataille parmi les algorithmes d'apprentissage - descente de propagation vers l'arrière du gradient stochastique. Cependant, nous rencontrerons un problème - nos STS ne fonctionneront pas beaucoup mieux (voire pas du tout) que ceux peu profonds.

Cet échec semble étrange à la lumière de la discussion ci-dessus. Mais au lieu d'abandonner le STS, nous allons approfondir le problème et essayer de comprendre pourquoi le STS est difficile à former. Lorsque nous examinons de plus près le problème, nous constatons que différentes couches du STS apprennent à des vitesses très différentes. En particulier, lorsque les dernières couches du réseau sont bien formées, les premières sont souvent bloquées pendant la formation et n'apprennent presque rien. Et ce n'est pas seulement de la malchance. Nous trouverons des raisons fondamentales pour ralentir l'apprentissage qui sont liées à l'utilisation de techniques d'apprentissage basées sur un gradient.

En creusant plus profondément dans ce problème, nous découvrons que le phénomène inverse peut également se produire: les premières couches peuvent bien apprendre et les dernières se coincent. En fait, nous découvrirons l'instabilité interne associée à la formation de descente en gradient dans les NS multicouches profondes. Et en raison de cette instabilité, les couches précoces ou tardives sont souvent bloquées à l'entraînement.

Tout cela semble assez désagréable. Mais plongés dans ces difficultés, nous pouvons commencer à développer des idées sur ce qui doit être fait pour une formation efficace des STS. Par conséquent, ces études seront une bonne préparation pour le prochain chapitre, où nous utiliserons l'apprentissage en profondeur pour aborder les problèmes de reconnaissance d'image.

Problème de gradient de décoloration

Alors, qu'est-ce qui ne va pas lorsque nous essayons de former un réseau profond?

Pour répondre à cette question, nous revenons au réseau ne contenant qu'une seule couche cachée. Comme d'habitude, nous utiliserons le problème de classification des chiffres du MNIST comme un bac à sable pour l'apprentissage et l'expérimentation.

Si vous souhaitez répéter toutes ces étapes sur votre ordinateur, vous devez avoir installé Python 2.7, la bibliothèque Numpy et une copie du code qui peut être extrait du référentiel:

git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git 

Vous pouvez vous passer de git en téléchargeant simplement les données et le code . Accédez au sous-répertoire src et à partir du shell python, chargez les données MNIST:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() 

Configurez le réseau:

 >>> import network2 >>> net = network2.Network([784, 30, 10]) 

Un tel réseau a 784 neurones dans la couche d'entrée, correspondant à 28 × 28 = 784 pixels de l'image d'entrée. Nous utilisons 30 neurones cachés et 10 week-ends, correspondant à dix options de classification possibles pour les nombres MNIST ('0', '1', '2', ..., '9').

Essayons de former notre réseau pendant 30 époques entières à l'aide de mini-packages de 10 exemples de formation à la fois, vitesse d'apprentissage η = 0,1 et paramètre de régularisation λ = 5,0. Pendant la formation, nous suivrons l'exactitude de la classification via validation_data:

 >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

Nous obtenons une précision de classification de 96,48% (ou plus - les chiffres varieront selon les lancements), comparable à nos résultats précédents avec des paramètres similaires.

Ajoutons une autre couche cachée, contenant également 30 neurones, et essayons de former le réseau avec les mêmes hyperparamètres:

 >>> net = network2.Network([784, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

La précision de la classification s'améliore à 96,90%. C'est inspirant - une légère augmentation de la profondeur aide. Ajoutons une autre couche cachée de 30 neurones:

 >>> net = network2.Network([784, 30, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

Ça n'a pas aidé. Le résultat est même tombé à 96,57%, une valeur proche du réseau peu profond d'origine. Et si nous ajoutons une autre couche cachée:

 >>> net = network2.Network([784, 30, 30, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

Ensuite, la précision de classification chutera à nouveau, déjà à 96,53%. Statistiquement, cette baisse est probablement insignifiante, mais elle n'a rien de bon.

Ce comportement semble étrange. Il semble intuitivement que des couches cachées supplémentaires devraient aider le réseau à apprendre des fonctions de classification plus complexes et à mieux faire face à la tâche. Bien sûr, le résultat ne devrait pas empirer, car dans le pire des cas, des couches supplémentaires ne feront tout simplement rien. Mais cela ne se produit pas.

Alors qu'est-ce qui se passe? Supposons que des couches cachées supplémentaires peuvent aider en principe, et que le problème est que notre algorithme d'apprentissage ne trouve pas les valeurs correctes pour les poids et les décalages. Nous aimerions comprendre ce qui ne va pas avec notre algorithme et comment l'améliorer.

Pour comprendre ce qui s'est mal passé, visualisons le processus d'apprentissage du réseau. Ci-dessous, j'ai construit une partie du réseau [784,30,30,10], dans laquelle il y a deux couches cachées, chacune ayant 30 neurones cachés. Sur le diagramme, chaque neurone a une barre indiquant le taux de changement dans le processus d'apprentissage du réseau. Une grande barre signifie que les poids et les déplacements du neurone changent rapidement, et une petite signifie qu'ils changent lentement. Plus précisément, la barre désigne le gradient ∂C / ∂b du neurone, c'est-à-dire le taux de variation du coût par rapport au déplacement. Dans le chapitre 2, nous avons vu que cette valeur de gradient contrôle non seulement le taux de changement de déplacement pendant l'entraînement, mais aussi le taux de changement des poids des neurones d'entrée. Ne vous inquiétez pas si vous ne vous souvenez pas de ces détails: il suffit de garder à l'esprit que ces barres indiquent à quelle vitesse les poids et les déplacements des neurones changent pendant l'entraînement du réseau.

Pour simplifier le diagramme, j'ai dessiné seulement six neurones supérieurs dans deux couches cachées. J'ai abaissé les neurones entrants car ils n'ont ni poids ni biais. J'ai également omis les neurones de sortie, car nous comparons deux couches, et il est logique de comparer les couches avec le même nombre de neurones. Le diagramme a été construit à l'aide du programme generate_gradient.py au tout début de la formation, c'est-à-dire immédiatement après l'initialisation du réseau.



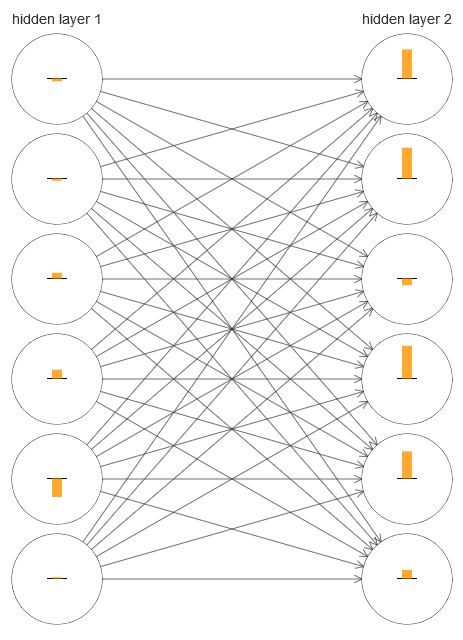
Le réseau a été initialisé par hasard, donc cette diversité dans la vitesse d'entraînement des neurones n'est pas surprenante. Cependant, il attire immédiatement l'attention que dans la deuxième couche cachée, les bandes sont fondamentalement beaucoup plus que dans la première. En conséquence, les neurones de la deuxième couche apprendront beaucoup plus rapidement que dans la première. Est-ce une coïncidence ou les neurones de la deuxième couche sont-ils susceptibles d'apprendre en général plus rapidement que les neurones de la première?

Pour savoir exactement, il sera bon d'avoir une manière générale de comparer la vitesse d'apprentissage dans les première et deuxième couches cachées. Pour ce faire, notons le gradient comme δ ^l _j = ∂C / ∂b ^l _j , c'est-à-dire comme le gradient du neurone n ° j dans la couche n ° l. Dans le deuxième chapitre, nous l'avons appelé une «erreur», mais ici je l'appellerai officieusement un «gradient». Informellement - puisque cette valeur n'inclut pas explicitement les dérivées partielles du coût en poids, ∂C / ∂w. Le gradient δ ¹ peut être considéré comme un vecteur dont les éléments déterminent la vitesse d'apprentissage de la première couche cachée, et δ ² comme un vecteur dont les éléments déterminent la vitesse d'apprentissage de la deuxième couche cachée. Nous utilisons les longueurs de ces vecteurs comme des estimations approximatives de la vitesse d'apprentissage des couches. C'est, par exemple, la longueur || δ ¹ || mesure la vitesse d'apprentissage de la première couche cachée et la longueur || δ ² || mesure la vitesse d'apprentissage de la deuxième couche cachée.

Avec de telles définitions et la même configuration que ci-dessus, nous constatons que || δ ¹ || = 0,07 et || δ ² || = 0,31. Cela confirme nos soupçons: les neurones de la deuxième couche cachée apprennent beaucoup plus rapidement que les neurones de la première couche cachée.

Que se passe-t-il si nous ajoutons plus de couches cachées? Avec trois couches cachées dans le réseau [784,30,30,30,10], les vitesses d'apprentissage correspondantes seront 0,012, 0,060 et 0,283. Encore une fois, les premières couches cachées apprennent beaucoup plus lentement que la précédente. Ajoutez une autre couche cachée avec 30 neurones. Dans ce cas, les vitesses d'apprentissage correspondantes seront de 0,003, 0,017, 0,070 et 0,285. Le motif est préservé: les premières couches apprennent plus lentement que les dernières.

Nous avons étudié la vitesse d'apprentissage au tout début - juste après l'initialisation du réseau. Comment cette vitesse change-t-elle à mesure que vous apprenez? Revenons en arrière et regardons le réseau avec deux couches cachées. La vitesse d'apprentissage change comme ceci:



Pour obtenir ces résultats, j'ai utilisé une descente de gradient par lots avec 1000 images d'entraînement et une formation pour 500 époques. Ceci est légèrement différent de nos procédures habituelles - je n'ai pas utilisé de mini-packages et n'ai pris que 1000 images de formation, au lieu d'un ensemble complet de 50 000 pièces. Je n'essaie pas de vous tromper et de vous tromper, mais il s'avère que l'utilisation de la descente de gradient stochastique avec des mini-paquets apporte beaucoup plus de bruit aux résultats (mais si vous faites la moyenne du bruit, les résultats sont similaires). En utilisant les paramètres que j'ai choisis, il est facile de lisser les résultats afin que nous puissions voir ce qui se passe.

En tout cas, comme on le voit, deux couches commencent à s'entraîner à deux vitesses très différentes (que nous connaissons déjà). Ensuite, la vitesse des deux couches diminue très rapidement, après quoi un rebond se produit. Cependant, pendant tout ce temps, la première couche cachée apprend beaucoup plus lentement que la seconde.

Qu'en est-il des réseaux plus complexes? Voici les résultats d'une expérience similaire, mais avec un réseau à trois couches cachées [784,30,30,30,10]:



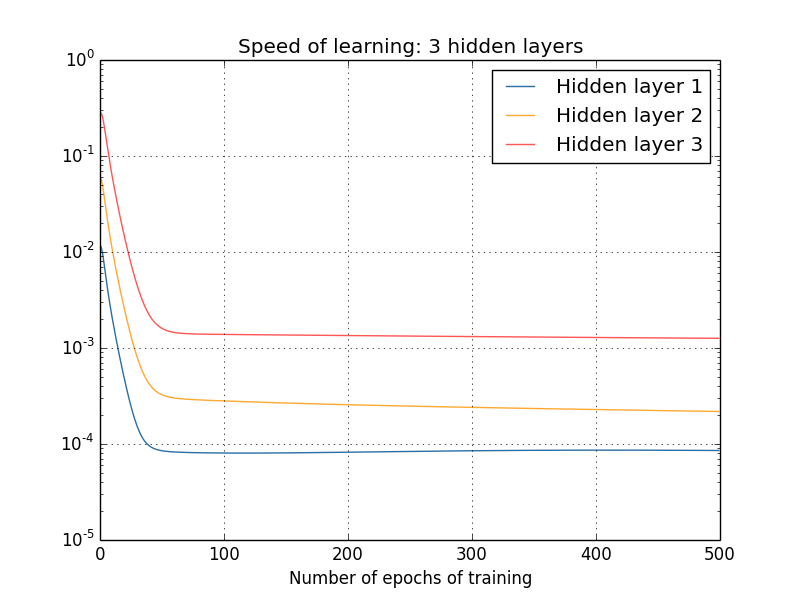
Et encore une fois, les premières couches cachées apprennent beaucoup plus lentement que la précédente. Enfin, essayons d'ajouter une quatrième couche cachée (réseau [784,30,30,30,30,10]) et voyons ce qui se passe lorsqu'elle est entraînée:



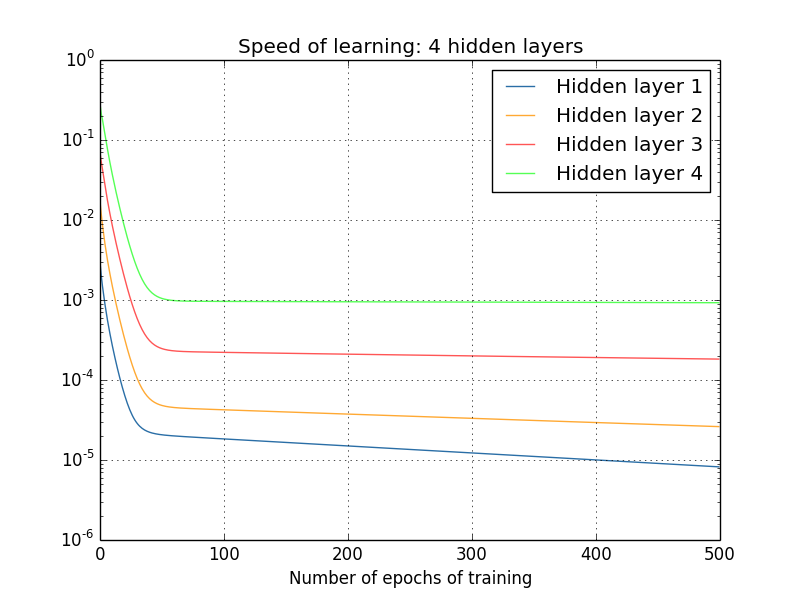
Et encore une fois, les premières couches cachées apprennent beaucoup plus lentement que la précédente. Dans ce cas, la première couche cachée apprend environ 100 fois plus lentement que la précédente. Pas étonnant que nous ayons eu de tels problèmes pour apprendre ces réseaux!

Nous avons fait une observation importante: au moins dans certains GNS, le gradient diminue en se déplaçant dans la direction opposée le long des couches cachées. C'est-à-dire que les neurones des premières couches sont entraînés beaucoup plus lentement que les neurones des derniers. Et bien que nous ayons observé cet effet dans un seul réseau, il existe des raisons fondamentales pour lesquelles cela se produit dans de nombreux NS. Ce phénomène est connu sous le nom de «problème du gradient de fuite» (voir travaux 1 , 2 ).

Pourquoi y a-t-il un problème de gradient de décoloration? Existe-t-il des moyens de l'éviter? Comment pouvons-nous y faire face lors de la formation STS? En fait, nous découvrirons bientôt que ce n'est pas inévitable, bien que l'alternative ne lui semble pas très attrayante: parfois dans les premières couches le gradient est beaucoup plus grand! C'est déjà un problème de croissance explosive de gradient, et il n'est pas plus bon en lui que dans le problème de la disparition d'un gradient. En général, il s'avère que le gradient dans le STS est instable, et est sujet à une croissance explosive ou à disparaître dans les premières couches. Cette instabilité est un problème fondamental pour la formation GNS à gradient. C'est ce que nous devons comprendre et éventuellement le résoudre d'une manière ou d'une autre.

L'une des réactions à un gradient qui s'estompe (ou qui est instable) est de se demander s'il s'agit réellement d'un problème grave? Détournons-nous brièvement de la NS et imaginons que nous essayons de minimiser numériquement la fonction f (x) d'une variable. Ne serait-ce pas bien si la dérivée f ′ (x) était petite? Cela ne signifierait-il pas que nous sommes déjà proches de l'extrême? Et de la même manière, un petit gradient dans les premières couches du GNS ne signifie-t-il pas que nous n'avons plus besoin d'ajuster fortement les poids et les déplacements?

Bien sûr que non. Rappelons que nous avons initialisé au hasard les poids et les décalages du réseau. Il est hautement improbable que nos poids et mélanges d'origine soient bien adaptés à ce que nous attendons de notre réseau. Comme exemple spécifique, considérons la première couche de poids dans le réseau [784,30,30,30,10], qui classe les nombres MNIST. L'initialisation aléatoire signifie que la première couche éjecte la plupart des informations sur l'image entrante. Même si les couches ultérieures étaient soigneusement formées, il leur serait extrêmement difficile de déterminer le message entrant, simplement en raison d'un manque d'informations. Par conséquent, il est absolument impossible d'imaginer que la première couche n'a tout simplement pas besoin d'être formée. Si nous allons former STS, nous devons comprendre comment résoudre le problème de la disparition d'un gradient.

Qu'est-ce qui cause le problème du gradient de décoloration? Gradients instables dans GNS

Pour comprendre comment le problème d'un gradient disparaissant apparaît, considérons le NS le plus simple: avec un seul neurone dans chaque couche. Voici un réseau avec trois couches cachées:



Ici w ₁ , w ₂ , ... sont des poids, b ₁ , b ₂ , ... sont des déplacements, C est une certaine fonction de coût. Pour rappel, je dirai que la sortie a _j du neurone n ° j est égale à σ (z _j ), où σ est la fonction d'activation sigmoïde habituelle, et z _j = w _j a _{j - 1} + b _j est l'entrée pondérée du neurone. J'ai décrit la fonction de coût à la fin pour souligner que le coût est fonction de la sortie du réseau, et ₄ : si la sortie réelle est proche de ce que vous voulez, alors le coût sera petit, et si loin, alors il sera grand.

Nous étudions le gradient ∂C / ∂b ₁ associé au premier neurone caché. Nous trouvons l'expression de ∂C / ∂b ₁ et, après l'avoir étudiée, nous comprendrons pourquoi le problème du gradient de fuite se pose.

Nous commençons par démontrer l'expression de ∂C / ∂b ₁ . Il semble imprenable, mais en fait sa structure est simple, et je vais le décrire bientôt. Voici cette expression (pour l'instant, ignorez le réseau lui-même et notez que σ n'est qu'un dérivé de la fonction σ):



La structure de l'expression est la suivante: pour chaque neurone du réseau il y a un terme de multiplication σ ′ (z _j ), pour chaque poids il y a w _j , et il y a aussi le dernier terme, ∂C / ∂a ₄ , correspondant à la fonction de coût. Notez que j'ai placé les membres correspondants au-dessus des parties correspondantes du réseau. Par conséquent, le réseau lui-même est une règle d'expression mnémonique.

Vous pouvez prendre cette expression sur la foi et sauter sa discussion jusqu'à l'endroit où il est expliqué comment elle se rapporte au problème du gradient de décoloration. Il n'y a rien de mal à cela, car cette expression est un cas particulier de notre discussion sur la rétropropagation. Cependant, il est facile d'expliquer sa fidélité, il sera donc assez intéressant (et peut-être instructif) d'étudier cette explication.

Imaginez que nous avons fait un petit changement de Δb ₁ au décalage b ₁ . Cela enverra une série de modifications en cascade sur le reste du réseau. Tout d'abord, cela entraînera une modification de la sortie du premier neurone caché Δa ₁ . Ceci, à son tour, force Δz ₂ à changer l'entrée pondérée du deuxième neurone caché. Ensuite, il y aura un changement de Δa ₂ dans la sortie du deuxième neurone caché. Et ainsi de suite, jusqu'à un changement de ΔC dans la valeur de sortie. Il s'avère que:

$$

$$\ frac {\ partial C} {\ partial b_1} \ approx \ frac {\ Delta C} {\ Delta b_1} \ tag {114}$$

Cela suggère que nous pouvons dériver une expression pour le gradient ∂C / ∂b ₁ , en surveillant attentivement l'influence de chaque étape de cette cascade.

Pour ce faire, réfléchissons à la façon dont Δb ₁ fait changer la sortie a _{1 du} premier neurone caché. On a ₁ = σ (z ₁ ) = σ (w ₁ a ₀ + b ₁ ), donc

$$

$$\ Delta a_1 \ approx \ frac {\ partial \ sigma (w_1 a_0 + b_1)} {\ partial b_1} \ Delta b_1 \ tag {115}$$

$$

$$= \ sigma '(z_1) \ Delta b_1 \ tag {116}$$

Le terme σ ′ (z ₁ ) devrait sembler familier: c'est le premier terme de notre expression pour le gradient ∂C / ∂b ₁ . Intuitivement, il transforme le changement du décalage Δb ₁ en changement Δa _{1 de l'} activation _{de la} sortie. Le changement de Δa ₁ entraîne à son tour un changement de l'entrée pondérée z ₂ = w ₂ a ₁ + b _{2 du} deuxième neurone caché:

$$

$$\ Delta z_2 \ approx \ frac {\ partial z_2} {\ partial a_1} \ Delta a_1 \ tag {117}$$

$$

$$= w_2 \ Delta a_1 \ tag {118}$$

En combinant les expressions pour Δz ₂ et Δa ₁ , nous voyons comment le changement de biais b _{1 se} propage le long du réseau et affecte z ₂ :

$$

$$\ Delta z_2 \ approx \ sigma '(z_1) w_2 \ Delta b_1 \ tag {119}$$

Et cela devrait aussi être familier: ce sont les deux premiers termes de notre expression déclarée pour le gradient ∂C / ∂b ₁ .

Cela peut être poursuivi davantage en surveillant la façon dont les changements se propagent dans le reste du réseau. Sur chaque neurone, nous sélectionnons le terme σ ′ (z _j ), et à travers chaque poids, nous sélectionnons le terme w _j . En conséquence, une expression est obtenue qui relie le changement final ΔC de la fonction de coût au changement initial Δb _{1 du} biais:

$$

$$\ Delta C \ approx \ sigma '(z_1) w_2 \ sigma' (z_2) \ ldots \ sigma '(z_4) \ frac {\ partial C} {\ partial a_4} \ Delta b_1 \ tag {120}$$

En le divisant par Δb ₁ , nous obtenons vraiment l'expression souhaitée pour le gradient:

$$

$$\ frac {\ partial C} {\ partial b_1} = \ sigma '(z_1) w_2 \ sigma' (z_2) \ ldots \ sigma '(z_4) \ frac {\ partial C} {\ partial a_4} \ tag { 121}$$

Pourquoi y a-t-il un problème de gradient de décoloration?

Pour comprendre pourquoi le problème du gradient disparaissant se pose, écrivons en détail toute notre expression pour le gradient:

$$

$$\ frac {\ partial C} {\ partial b_1} = \ sigma '(z_1) \ w_2 \ sigma' (z_2) \ w_3 \ sigma '(z_3) \, w_4 \ sigma' (z_4) \ \ frac {\ partiel C} {\ partiel a_4} \ tag {122}$$

En plus du dernier terme, cette expression est le produit de termes de la forme w _j σ ′ (z _j ). Pour comprendre comment chacun d'eux se comporte, nous regardons le graphe de la fonction σ:



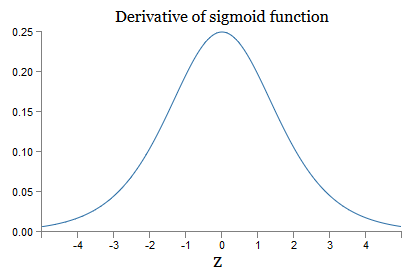
Le graphique atteint un maximum au point σ ′ (0) = 1/4. Si nous utilisons l'approche standard pour initialiser les pondérations du réseau, nous sélectionnons les pondérations en utilisant la distribution gaussienne, c'est-à-dire la moyenne quadratique zéro et l'écart-type 1. Par conséquent, les pondérations satisfont généralement l'inégalité | w _j | <1. En comparant toutes ces observations, nous voyons que les termes w _j σ ′ (z _j ) satisfont généralement l'inégalité | w _j σ ′ (z _j ) | <1/4. Et si nous prenons le produit de l'ensemble de ces termes, il diminuera de façon exponentielle: plus il y a de termes, plus le produit est petit. Cela commence à apparaître comme une solution possible au problème de la disparition du gradient.

Pour écrire cela plus précisément, nous comparons l'expression de ∂C / ∂b ₁ avec l'expression du gradient par rapport au décalage suivant, par exemple, ∂C / ∂b ₃ . Bien sûr, nous n'avons pas écrit d'expression détaillée pour ∂C / ∂b ₃ , mais elle suit les mêmes lois que celles décrites ci-dessus pour ∂C / ∂b ₁ . Et voici une comparaison de deux expressions:



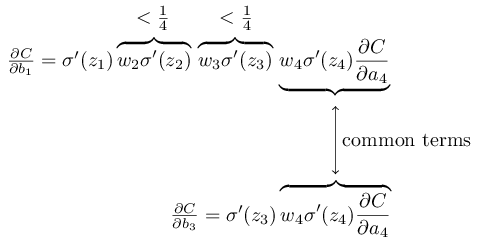
Ils ont plusieurs membres communs. Cependant, le gradient ∂C / ∂b ₁ comprend deux termes supplémentaires, chacun ayant la forme w _j σ ′ (z _j ). Comme nous l'avons vu, ces termes ne dépassent généralement pas 1/4. Par conséquent, le gradient ∂C / ∂b ₁ sera généralement 16 (ou plus) fois plus petit que ∂C / ∂b ₃ . Et c'est la principale cause de la disparition du problème de gradient.

Bien sûr, ce n'est pas une preuve exacte mais informelle du problème. Il y a plusieurs mises en garde. En particulier, on peut être intéressé à savoir si les poids w _j augmenteront pendant l'entraînement. Si cela se produit, les termes w _j σ ′ (z _j ) dans le produit ne satisferont plus l'inégalité | w _j σ ′ (z _j ) | <1/4. Et si elles s'avèrent être assez grandes, supérieures à 1, alors nous n'aurons plus le problème d'un gradient de décoloration. Au lieu de cela, le dégradé augmentera de façon exponentielle lorsque vous reviendrez à travers les couches. Et au lieu de disparaître le problème du gradient, nous obtenons le problème de la croissance explosive du gradient.

Le problème de la croissance explosive du gradient

Regardons un exemple spécifique d'un gradient explosif. L'exemple sera quelque peu artificiel: j'ajusterai les paramètres du réseau afin de garantir la survenue d'une croissance explosive. Mais bien que l'exemple soit artificiel, son plus est qu'il démontre clairement que la croissance explosive du gradient n'est pas une possibilité hypothétique, mais cela peut vraiment se produire.

Pour une croissance explosive en gradient, vous devez suivre deux étapes. Tout d'abord, nous choisissons des poids importants dans l'ensemble du réseau, par exemple, w1 = w2 = w3 = w4 = 100. Ensuite, nous choisissons de tels décalages pour que les termes σ ′ (z _j ) ne soient pas trop petits. Et c'est assez facile à faire: il suffit de sélectionner de tels déplacements pour que l'entrée pondérée de chaque neurone soit zj = 0 (puis σ ′ (z _j ) = 1/4). Par conséquent, par exemple, nous avons besoin de z ₁ = w ₁ a ₀ + b ₁ = 0. Ceci peut être réalisé en définissant b ₁ = −100 ∗ a ₀ . La même idée peut être utilisée pour sélectionner d'autres décalages. En conséquence, nous verrons que tous les termes w _j σ ′ (z _j ) s'avèrent être égaux à 100 ∗ 14 = 25. Et puis nous obtenons une croissance explosive en gradient.

Problème de gradient instable

Le problème fondamental n'est pas la disparition du problème du gradient ou la croissance explosive du gradient. C'est que le dégradé dans les premières couches est le produit des membres de toutes les autres couches. Et quand il y a plusieurs couches, la situation devient essentiellement instable. Et la seule façon dont toutes les couches peuvent apprendre à peu près à la même vitesse est de choisir de tels membres du travail qui s'équilibreront. Et en l'absence de mécanisme ou de raison pour un tel équilibrage, il est peu probable que cela se produise par hasard.Bref, le vrai problème est que NS souffre du problème d'un gradient instable. Et à la fin, si nous utilisons des techniques d'apprentissage basées sur un gradient standard, différentes couches du réseau apprendront à des vitesses terriblement différentes.

Exercice

• , |σ′(z)|<1/4. , , . ?

Nous avons vu que le gradient peut disparaître ou croître de façon explosive dans les premières couches d'un réseau profond. En fait, lors de l'utilisation de neurones sigmoïdes, le gradient disparaît généralement. Pour comprendre pourquoi, considérons à nouveau l'expression | wσ ′ (z) |. Pour éviter la disparition du problème de gradient, nous avons besoin de | wσ ′ (z) | ≥1. Vous pouvez décider que cela est facile à réaliser avec de très grandes valeurs de w. Cependant, en réalité, ce n'est pas si simple. La raison en est que le terme σ ′ (z) dépend également de w: σ ′ (z) = σ ′ (wa + b), où a est l'activation d'entrée. Et si nous faisons w grand, nous devons essayer de ne pas faire σ ′ (wa + b) petit en parallèle. Et cela s'avère être une sérieuse limitation. La raison en est que lorsque nous faisons w gros, nous faisons wa + b très gros. Si vous regardez le graphe de σ ′, on peut voir que cela nous conduit aux «ailes» de la fonction σ ′,où il prend de très petites valeurs. Et la seule façon d'éviter cela est de conserver l'activation entrante dans une plage de valeurs assez étroite. Parfois, cela se produit par accident. Mais le plus souvent, cela ne se produit pas. Par conséquent, dans le cas général, nous avons le problème d'un gradient de fuite.

• |wσ′(wa+b)|. , |wσ′(wa+b)|≥1. , , |w|≥4.
• , |w|≥4, , |wσ′(wa+b)|≥1.
• , , ,

  $$

  $$\frac{2}{|w|} \ln\left( \frac{|w|(1+\sqrt{1-4/|w|})}{2}-1\right) \tag{123}$$
• , |w|≈6.9, ≈0,45. , , , .
• . x, w ₁ , b w ₂ . , , , w ₂ σ(w ₁ x+b)≈x for x∈[0,1]. , , ( ). : x=1/2+Δ, , w ₁ , w ₁ Δ .

Nous avons étudié les réseaux de jouets avec un seul neurone dans chaque couche cachée. Qu'en est-il des réseaux profonds plus complexes qui ont de nombreux neurones dans chaque couche cachée?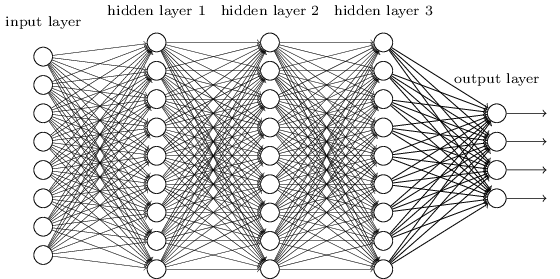



En fait, la même chose se produit dans de tels réseaux. Plus tôt dans le chapitre sur la propagation arrière, nous avons vu que le gradient dans la couche #l d'un réseau avec L couches est spécifié comme:

$$

$$\delta^l = \Sigma'(z^l) (w^{l+1})^T \Sigma'(z^{l+1}) (w^{l+2})^T \ldots \Sigma'(z^L) \nabla_a C \tag{124}$$

Ici Σ ′ (z ^l ) est la matrice diagonale, dont les éléments sont les valeurs de σ ′ (z) pour les entrées pondérées de la couche n ° l. w ^l sont des matrices de poids pour différentes couches. Et ∇ _a C est le vecteur des dérivées partielles de C par rapport aux activations de sortie.

Cette expression est beaucoup plus compliquée que dans le cas d'un neurone. Et pourtant, si vous regardez de près, son essence sera très similaire, avec un tas de paires de la forme (w ^j ) ^T Σ ′ (z ^j ). De plus, les matrices Σ ′ (z ^j ) en diagonale ont de petites valeurs, pas plus de 1/4. Si les matrices de poids w ^j ne sont pas trop grandes, chaque terme supplémentaire (w ^j ) ^T Σ ′ (z ^l) tend à réduire le vecteur de gradient, ce qui entraîne une disparition du gradient. Dans le cas général, un plus grand nombre de termes de multiplication conduit à un gradient instable, comme dans notre exemple précédent. En pratique, empiriquement généralement dans les réseaux sigmoïdes, les gradients dans les premières couches disparaissent exponentiellement rapidement. En conséquence, l'apprentissage dans ces couches ralentit. Et le ralentissement n'est pas un accident ou un inconvénient: c'est une conséquence fondamentale de notre approche d'apprentissage choisie.

Autres obstacles à l'apprentissage en profondeur

Dans ce chapitre, je me suis concentré sur la décoloration des gradients - et plus généralement le cas des gradients instables - en tant qu'obstacle à l'apprentissage en profondeur. En fait, les gradients instables ne sont qu'un obstacle au développement de la protection civile, quoique important et fondamental. Une partie importante de la recherche actuelle tente de mieux comprendre les problèmes qui peuvent survenir dans l'enseignement du GO. Je ne décrirai pas en détail tous ces travaux, mais je veux mentionner brièvement quelques travaux pour vous donner une idée de certaines questions posées par les gens.

Comme premier exemple en 2010il a été démontré que l'utilisation des fonctions d'activation sigmoïde peut entraîner des problèmes d'apprentissage de la NS. En particulier, des preuves ont été trouvées que l'utilisation d'un sigmoïde conduira au fait que les activations de la dernière couche cachée pendant l'entraînement seront saturées dans la région 0, ce qui ralentira sérieusement l'entraînement. Plusieurs fonctions d'activation alternatives ont été proposées qui ne souffrent pas tant du problème de saturation (voir aussi un autre document de travail ).

À titre de premier exemple, en 2013, l'effet de l'initialisation aléatoire des poids et du graphique des impulsions dans une descente de gradient stochastique basé sur une impulsion a été étudié sur le GO. Dans les deux cas, un bon choix a significativement influencé la capacité à former des STS.

Ces exemples suggèrent que la question «Pourquoi STS est-il si difficile à former?» très compliqué. Dans ce chapitre, nous nous sommes concentrés sur les instabilités associées à la formation de gradient de GNS. Les résultats des deux paragraphes précédents indiquent que le choix de la fonction d'activation, la méthode d'initialisation des poids et même les détails de la mise en œuvre de l'entraînement basé sur la descente de gradient jouent également un rôle. Et, bien sûr, le choix de l'architecture du réseau et d'autres hyperparamètres sera important. Par conséquent, de nombreux facteurs peuvent jouer un rôle dans la difficulté d'apprendre des réseaux profonds, et la question de la compréhension de ces facteurs fait l'objet de recherches continues. Mais tout cela semble plutôt sombre et inspire le pessimisme. Cependant, il y a de bonnes nouvelles - dans le prochain chapitre, nous allons tout emballer en notre faveur, et nous développerons plusieurs approches dans GO,qui, dans une certaine mesure, pourront surmonter ou contourner tous ces problèmes.