Beaucoup pensent que seule la physique quantique peut être plus compliquée que la physique classique. Cependant, il est beaucoup plus difficile d'étudier des systèmes qui sont, pour ainsi dire, à la jonction de ces deux mondes. Si de plus en plus de particules sont ajoutées à un système quantique, il commencera à perdre ses propriétés quantiques et à se transformer en un système plus classique. Ce processus est appelé la transition quantique-classique. Les ordinateurs classiques ne suffiront pas pour étudier un tel système, car les scientifiques du Los Alamos National Laboratory ont proposé leur propre algorithme, qui, associé à des ordinateurs quantiques de quelques centaines de qubits, peut résoudre les secrets de la transition quantique-classique. Comment l'algorithme fonctionne, pourquoi moins de formules signifient mieux et quelle application de cet algorithme dans la pratique? Ceci et pas seulement nous apprenons du rapport du groupe de recherche. Allons-y.
Base d'étude
Une transition quantique-classique, si elle est exagérée, est un processus de décohérence lorsqu'un système quantique perd sa cohérence, c'est-à-dire acquiert des caractéristiques classiques. Ce processus peut se produire pour un certain nombre de raisons, parmi lesquelles la plus évidente est l'interaction du système quantique et de l'environnement. On pense également que ce processus est la pierre sur laquelle le processus de réalisation d'un ordinateur quantique trébuche.
Il existe de nombreuses méthodes pour lutter contre la décohérence, l'une est plus divertissante que l'autre, mais au total, elles peuvent être divisées en deux catégories: l'isolement et la mise en œuvre. Dans le premier cas, les scientifiques tentent d'isoler le système quantique de l'environnement, en utilisant des températures très basses et / ou un vide poussé. Dans le second cas, des corrections (code) sont introduites dans les algorithmes de calculs quantiques, qui seront résistants aux erreurs dues à la décohérence. Ces méthodes fonctionnent, personne ne le nie, mais elles ne sont pas très évolutives. Les scientifiques peuvent maintenir les atomes dans un état de superposition pendant un certain temps si les influences environnementales sont minimisées. Cependant, à plus grande échelle, tout, en règle générale, va en enfer.
Ainsi, alors que certaines personnes intelligentes en blouse blanche cherchent des moyens de faire face à la décohérence, d'autres recherchent des outils pour l'étudier. Si vous voulez vaincre votre ennemi, sachez-le à vue, comme on dit.
Avant de plonger dans le flux de formules et d'explications concernant l'algorithme développé par les scientifiques, il vaut la peine de faire un petit saut dans le temps. Robert Griffiths, physicien américain à l'Université Carnegie Mellon, a proposé une théorie des histoires séquentielles (événements) en 1984: la physique classique est proche de la mécanique quantique, et les mathématiques quantiques peuvent calculer les probabilités de phénomènes à grande échelle et subatomiques qui ne se rapportent pas aux résultats de mesure, mais à la physique état du système. M. Griffiths donne comme exemple des photographies de montagnes qui peuvent être prises sous différents angles, puis faire une image d'une vraie montagne à partir d'elles. Dans le cas de la physique quantique, il est possible de choisir un paramètre de mesure, mais cela ne fonctionnera pas de combiner deux mesures pour composer une image complète d'une particule avant la mesure. Avant le processus réel de mesure de la position réelle et de l'élan, il n'existe tout simplement pas.
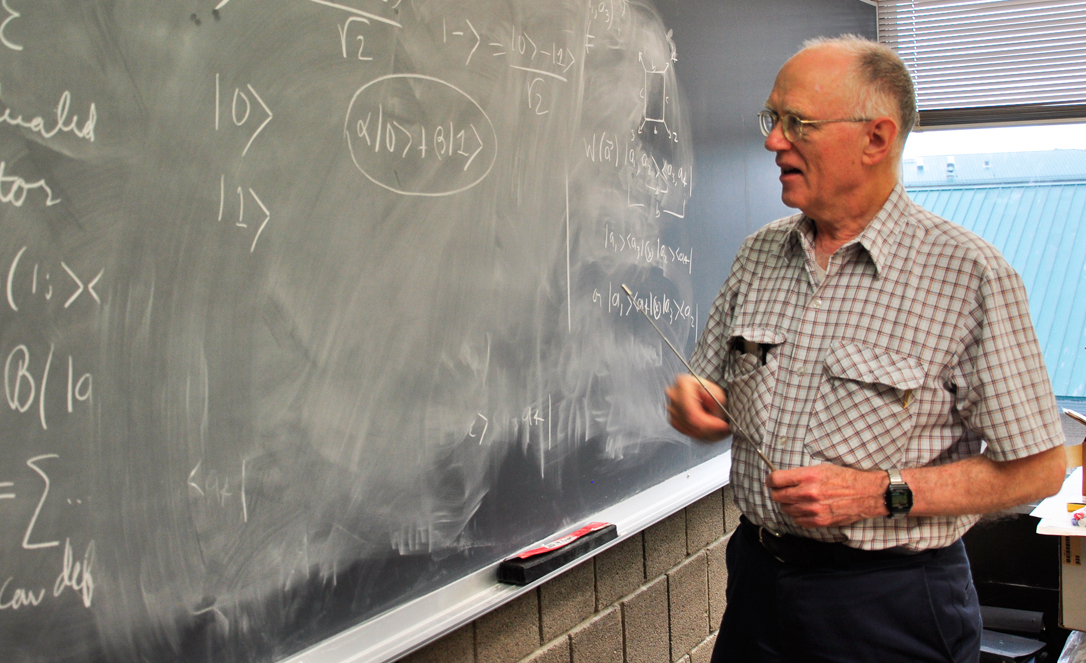Robert GriffithsConfus et soufflant un peu sur le toit, mais ce n'est pas tout. En 1989, Murray Gell-Mann et James Hartl ont présenté les leurs en se basant sur la théorie de Griffiths. À leur avis, l'Univers entier peut être considéré comme un système quantique unique sans environnement externe. Dans l'affirmative, la décohérence se produit au sein du système et le résultat de son activité est des domaines quasi-classiques - des ensembles d'histoires séquentielles qui ne se distinguent pas sur le fond du grain rugueux en raison de la décohérence.
Ces théories ont aidé à résoudre certains problèmes et paradoxes en mécanique quantique, mais pas tous. Les chercheurs pensent que les résultats de leurs prédécesseurs ne sont pas largement utilisés en raison du fait que les calculs de systèmes non triviaux (par exemple, des systèmes discrets de taille notable ou des systèmes continus qui ne permettent pas de descriptions approximatives par des intégrales exactement résolubles) sont extrêmement compliqués. En d'autres termes, ces théories sont bonnes, mais seulement dans des cas simples.
Ces dernières années, le développement des technologies quantiques s'est fortement accéléré et des algorithmes variationnels hybrides quantiques classiques (
VHQCA ) sont apparus capables de faire face à différentes tâches (factorisation, recherche d'états fondamentaux, etc.).
Dans le travail que nous envisageons aujourd'hui, les scientifiques décrivent leur algorithme VHQCA pour les histoires séquentielles. Selon les chercheurs, leur algorithme dépasse les méthodes classiques dans de nombreux paramètres, dont la taille des systèmes étudiés.
Marathon de formules (base théorique)
Nous avons déjà eu une digression historique, et maintenant il vaut la peine de se familiariser avec la base de calcul de l'algorithme avant de considérer les résultats de son travail.
La base des histoires séquentielles (CH) est l'histoire de
Y α est une séquence de propriétés dans une séquence d'instants temporels
t 1 <
t 2 <... <
t k :
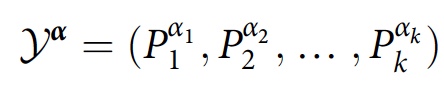
où
P α j j est sélectionné dans l'ensemble des projecteurs
P j qui sont sommés à l'instant
t j .
Les scientifiques donnent un exemple illustratif: un photon traversant plusieurs réseaux de diffraction puis frappant l'écran. Dans une telle situation, l'histoire peut être un photon passant par une fente dans le premier réseau, une autre fente dans le second, etc. Par conséquent, il y a une certaine interférence entre ces histoires. Et comme il y a des obstacles, il est impossible de additionner classiquement les probabilités de différentes histoires en prévision d'une prédiction correcte du point où le photon frappe l'écran.
Le cadre CH fournit des outils pour déterminer quand la famille d'histoire
F = {
Y α } présente des interférences, ce qui n'est pas toujours évident. Il définit également un opérateur de classe:
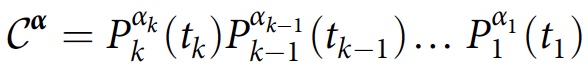
qui est un produit ordonné dans le temps des opérateurs de projection dans l'histoire de
Y α . Si le système est initialement décrit par une matrice de densité ρ, le degré d'interférence ou de chevauchement entre les historiques
Y α et
Y α ′ sera égal à:
Cette valeur est appelée la fonction de décohérence. La condition de cohérence pour la famille d'histoire
F dans ce cas ressemblera à ceci:
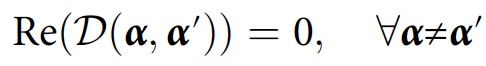
Ce n'est que si cette condition est satisfaite, pour l'historique de
Y α, que la probabilité sera
D (
α ,
α ). Pour des calculs plus simplifiés, une autre condition peut être appliquée:
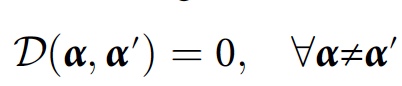
Les scientifiques disent que pour un algorithme numérique, il sera extrêmement utile de considérer la cohérence approximative tout en tenant compte des interférences mineures:
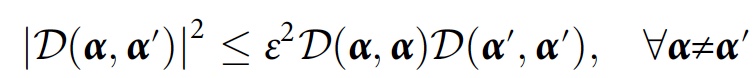
Pour étudier la cohérence qui découle uniquement de la décohérence (c'est-à-dire les enregistrements dans l'environnement), les chercheurs ont proposé une méthode qui prend plutôt une trace partielle sur
E , qui est un sous-système de l'environnement:
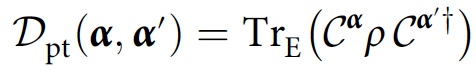
Avec cette modification, la condition de cohérence ressemblera à ceci:
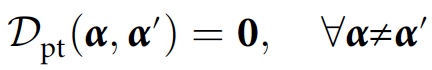
où 0 est la matrice zéro. Au lieu d'indiquer l'absence d'interférence environnementale, la cohérence indique la présence / absence de contradictions dans les enregistrements d'histoires dans l'environnement.
Image n ° 1: un schéma de branchement d'histoire pour k pas de temps.Compte tenu du marathon des formules et de la compréhension des histoires séquentielles, les scientifiques mettent en évidence le fait que les schémas numériques classiques pour CH ne sont pas en mesure de faire face à la tâche.
L'image ci-dessus montre un exemple où il y a des histoires de l'agrégat du nième nombre de particules avec 1/2 spin pour
k pas de temps. Le nombre d'histoires est de 2
nk ; il existe donc ~ 2
2 nk éléments fonctionnels de décohérence. De plus, l'estimation de chaque élément fonctionnel de décohérence
D (
α ,
α ' ) nécessite l'équivalent d'une simulation hamiltonienne du système, c'est-à-dire la multiplication de 2
n x 2
n matrices. Cela signifie que les clusters modernes auront besoin de centaines d'années pour calculer la cohérence d'une famille d'histoires avec
k = 2 pas de temps et
n = 10 tours.
Algorithme hybride VCH
Image n ° 2: schéma fonctionnel VCH.Les scientifiques ont appelé leur algorithme VHQCA VCH (histoires séquentielles variables). Le VCH prend en entrée le modèle physique (c'est-à-dire l'état initial
ρ et le hamiltonien
H ) et quelques
ansatz * pour les types de projecteurs à prendre en compte.
Ansatz * donne une idée de ce que devrait être la solution de l'équation et de sa forme.
Les données suivantes sont disponibles en tant que données résultantes:
- famille d'histoires F , qui est (approximativement) une trace complète et / ou partielle sous forme d'opérateurs de projection préparés sur un ordinateur quantique;
- probabilités des histoires les plus probables de Y α dans F (désolé pour le jeu de mots);
- estimation du paramètre de cohérence ε .
Le VCH comprend un cycle d'optimisation des paramètres où un ordinateur quantique évalue une fonction de coût qui quantifie l'inadéquation de la famille, tandis que l'optimiseur classique ajuste la famille (c'est-à-dire modifie les paramètres du projecteur) pour réduire les coûts.
Pour calculer les coûts, il faut tenir compte du fait que les éléments de la fonction de décohérence forment une matrice semi-définie positive. Cette propriété est utilisée dans VCH pour coder
D dans l'état quantique σ
A , dont les éléments matriciels sont ⟨α |
σ A |
α ′ ⟩ =
D (
α ,
α ′ ).
2b montre un circuit quantique qui prépare
σ A en transformant l'état initial
ρ ⊗ | 0〉 〈0 | dans les systèmes
SA (où
S modélise le système physique d'intérêt et
A est un système auxiliaire) à l'état
σ SA , dont la valeur limite est
σ A.Pour la cohérence de la trace complète de la matrice, une mesure globale de cohérence est introduite, qui détermine quantitativement à quelle distance
σ A est de la diagonale, qui sert de fonction des coûts:
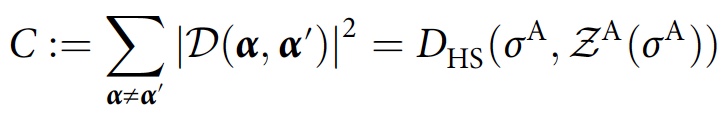
où
D HS est la distance de Hilbert-Schmidt et
Z A (
σ A ) est la version sans phase (tous les éléments hors diagonale sont mis à zéro) de
σ A.Cette quantité tend vers zéro si et seulement si
F est cohérent. Dans le cas d'une trace partielle, une fonction de coût similaire est obtenue, mais avec
σ A remplacé par
σ SA :
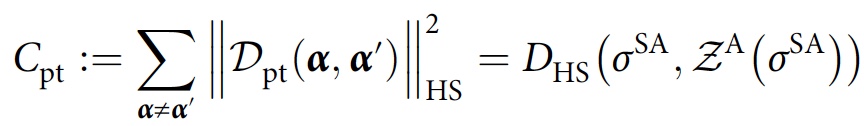
Le cycle d'optimisation des paramètres conduit à une famille approximativement cohérente d'histoires
F , où le paramètre de cohérence
ε est limité par le haut dans le cadre des coûts finaux.
2c montre la génération de probabilité pour les histoires les plus probables en préparant à plusieurs reprises σA et en mesurant sur une base standard, où les fréquences de mesure donnent les probabilités.
2e montre comment préparer un ensemble d'opérateurs de projection pour une histoire donnée dans
F.Résultats de l'expérience
Plusieurs expériences différentes utilisant l'algorithme VCH ont été réalisées. Nous en considérerons deux - un spin dans un champ magnétique et une molécule chirale.
Tourner dans un champ magnétique
Image n ° 3Dans la première expérience, nous avons considéré deux histoires temporelles d'une particule de spin 1/2 dans le champ magnétique
Bz , dont l'hamiltonien est
H = -
γBσ z . Les histoires que nous considérons ont un pas de temps Δt entre l'état initial et le premier projecteur, ainsi qu'entre le premier et le deuxième projecteur. De plus, il convient de noter que seuls les projecteurs sur le plan
xy de la sphère Bloch sont pris en compte.
L'image ci-dessus montre le tableau des coûts pour le processeur quantique ibmqx5, ainsi que pour le simulateur, dont la précision a été limitée en superposant les mêmes statistiques finales qui ont été collectées à l'aide du processeur quantique. Plusieurs creux trouvés lors de l'exécution de VCH sur ibmqx5 chevauchent le diagramme. Étant donné que ces minima correspondent assez bien à des familles théoriquement cohérentes, cela représente le succès de VCH dans la pratique.
Molécule chirale
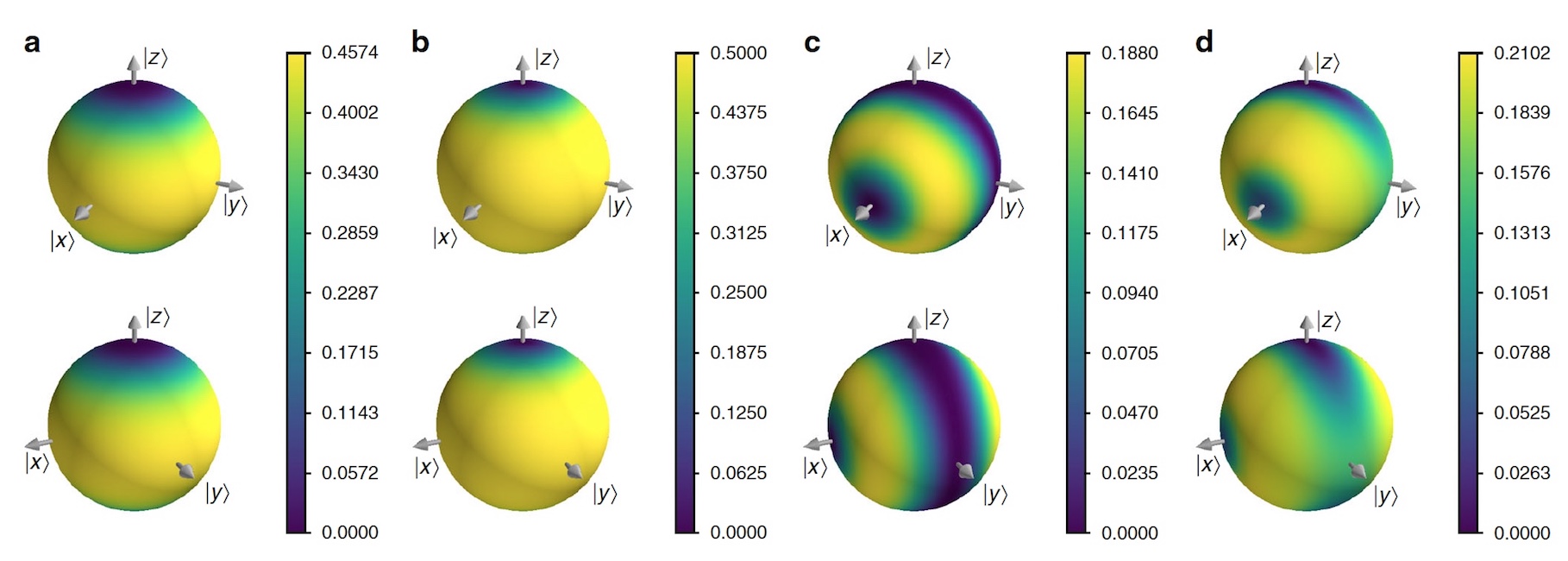Image n ° 4La molécule chirale a été choisie pour des expériences pratiques, car il s'agit d'un excellent moyen de déterminer l'application de VCH. La molécule chirale a été modélisée comme un système à deux niveaux dans lequel les états de chiralité droit | R〉 et gauche | L〉 sont décrits comme | R⟩ / | L⟩ = | +⟩ / | -⟩ = 1 / √2 * (| 0⟩ ± | 1⟩).
Une molécule chirale isolée tunnels entre | R⟩ et | L⟩, mais les scientifiques spéculent qu'elle se trouve dans un gaz, où les collisions avec d'autres molécules transmettent des informations sur la chiralité de la molécule à son environnement. Ce transfert d'information est modélisé par rotation selon un angle
θ x autour de l'axe
x d'un qubit moyen contrôlé par la chiralité du système.
Les scientifiques considèrent ensuite de simples familles d'histoires stationnaires, où un ensemble de projecteurs correspond à la même base tous les cinq fois (pour simplifier la modélisation, il a été constaté que la molécule entre en collision avec d'autres molécules 5 fois). En supposant que
θ z est l'angle de précession dû à la tunnellisation temporelle entre les collisions, il est alors possible d'étudier la concurrence entre la décohérence et la tunnellisation. L'image ci-dessus montre les résultats de cette simulation.
Les scientifiques notent un fait curieux - il y a une transition du régime quantique, où la chiralité n'est pas séquentielle, au régime classique, où la chiralité est à la fois séquentielle et stable dans le temps.
Pour une connaissance plus détaillée des nuances de l'étude, je vous recommande de consulter le
rapport des scientifiques et
les documents supplémentaires qui s'y rapportent.
Épilogue
Ce travail a démontré un nouvel algorithme qui, en conjonction avec les ordinateurs quantiques existants et futurs, peut mieux décrire un processus aussi complexe et déroutant qu'une transition quantique-classique. L'étude de ce phénomène est d'une grande importance si nous voulons un jour créer un ordinateur quantique réel, fonctionnel et efficace, dont le fonctionnement ne sera pas affecté par la décohérence.
L'algorithme VCH est au stade initial de développement, mais montre déjà ses performances. À l'avenir, les scientifiques ont naturellement l'intention de l'améliorer. Quoi qu'il en soit, les perspectives de mise en œuvre précoce de l'informatique quantique ne restent pas seulement au même niveau, mais augmentent avec chacune de ces études.
Merci de votre attention, restez curieux et bonne semaine de travail, les gars! :)
Merci de rester avec nous. Aimez-vous nos articles? Vous voulez voir des matériaux plus intéressants? Soutenez-nous en passant une commande ou en le recommandant à vos amis, une
réduction de 30% pour les utilisateurs Habr sur un analogue unique de serveurs d'entrée de gamme que nous avons inventés pour vous: Toute la vérité sur VPS (KVM) E5-2650 v4 (6 cœurs) 10 Go DDR4 240 Go SSD 1 Gbps à partir de 20 $ ou comment diviser le serveur? (les options sont disponibles avec RAID1 et RAID10, jusqu'à 24 cœurs et jusqu'à 40 Go de DDR4).
Dell R730xd 2 fois moins cher? Nous avons seulement
2 x Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 TV à partir de 199 $ aux Pays-Bas! Dell R420 - 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB - à partir de 99 $! Pour en savoir plus sur la
création d'un bâtiment d'infrastructure. classe utilisant des serveurs Dell R730xd E5-2650 v4 coûtant 9 000 euros pour un sou?