
Salut, habrozhiteli! La «modélisation prédictive en pratique» couvre tous les aspects de la prévision, en commençant par les étapes clés du prétraitement des données, le fractionnement des données et les principes de base de l'optimisation du modèle. Toutes les étapes de la modélisation sont considérées sur des exemples pratiques de la vie réelle, dans chaque chapitre un code détaillé en R est donné.
Ce livre peut être utilisé comme une introduction aux modèles prédictifs et un guide pour leur application. Les lecteurs qui n'ont pas de formation mathématique apprécieront les explications intuitives de méthodes spécifiques, et l'attention portée à la résolution de problèmes réels avec des données réelles aidera les spécialistes qui souhaitent améliorer leurs compétences.
Les auteurs ont essayé d'éviter les formules complexes, pour maîtriser le matériel de base, comprendre les concepts statistiques de base, tels que l'analyse de corrélation et de régression linéaire, est suffisant, mais des études mathématiques seront nécessaires pour étudier des sujets avancés.
Extrait. 7.5. Calculs
Cette section utilisera les fonctions des packages R caret, earth, kernlab et nnet.
R a de nombreux packages et fonctions pour créer des réseaux de neurones. Il s'agit notamment des packages nnet, neural et RSNNS. L'accent principal est mis sur le package nnet, qui prend en charge les modèles de base des réseaux de neurones avec un niveau de variables cachées, la réduction de poids, et se caractérise par une syntaxe relativement simple. RSNNS prend en charge un large éventail de réseaux de neurones. Notez que Bergmeir et Benitez (2012) ont une brève description des différents packages de réseaux de neurones dans R. Il fournit également un tutoriel sur RSNNS.
Réseaux de neurones
Pour approximer le modèle de régression, la fonction nnet peut recevoir à la fois la formule du modèle et l'interface matricielle. Pour la régression, la relation linéaire entre les variables cachées et la prévision est utilisée avec le paramètre linout = TRUE. L'appel le plus simple à la fonction de réseau neuronal ressemblera à:
> nnetFit <- nnet(predictors, outcome, + size = 5, + decay = 0.01, + linout = TRUE, + ## + trace = FALSE, + ## + ## .. + maxit = 500, + ## , + MaxNWts = 5 * (ncol(predictors) + 1) + 5 + 1)
Cet appel crée un modèle avec cinq variables cachées. On suppose que les données des prédicteurs ont été normalisées sur une seule échelle.
Pour faire la moyenne des modèles, la fonction avNNet du package caret est utilisée, qui a la même syntaxe:
> nnetAvg <- avNNet(predictors, outcome, + size = 5, + decay = 0.01, + ## + repeats = 5, + linout = TRUE, + ## + trace = FALSE, + ## + ## .. + maxit = 500, + ## , + MaxNWts = 5 * (ncol(predictors) + 1) + 5 + 1)
Les nouveaux points de données sont traités par la commande
> predict(nnetFit, newData) > ## > predict(nnetAvg, newData)
Pour reproduire la méthode présentée précédemment de sélection du nombre de variables cachées et de la quantité de réduction de poids par échantillonnage répété, nous appliquons la fonction train avec le paramètre method "" nnet "ou method =" avNNet ", en supprimant d'abord les prédicteurs (de sorte que la corrélation de paire absolue maximale entre les prédicteurs ne dépasse pas 0,75):
> ## findCorrelation > ## , > ## > tooHigh <- findCorrelation(cor(solTrainXtrans), cutoff = .75) > trainXnnet <- solTrainXtrans[, -tooHigh] > testXnnet <- solTestXtrans[, -tooHigh] > ## - : > nnetGrid <- expand.grid(.decay = c(0, 0.01, .1), + .size = c(1:10), + ## — + ## (. ) + ## . + .bag = FALSE) > set.seed(100) > nnetTune <- train(solTrainXtrans, solTrainY, + method = "avNNet", + tuneGrid = nnetGrid, + trControl = ctrl, + ## + ## + preProc = c("center", "scale"), + linout = TRUE, + trace = FALSE, + MaxNWts = 10 * (ncol(trainXnnet) + 1) + 10 + 1, + maxit = 500)
Splines de régression adaptative multidimensionnelle
Les modèles MARS sont contenus dans plusieurs packages, mais l'implémentation la plus étendue se trouve dans le package Earth. Un modèle MARS utilisant la phase nominale de passage direct et de troncature peut être appelé comme suit:
> marsFit <- earth(solTrainXtrans, solTrainY) > marsFit Selected 38 of 47 terms, and 30 of 228 predictors Importance: NumNonHAtoms, MolWeight, SurfaceArea2, SurfaceArea1, FP142, ... Number of terms at each degree of interaction: 1 37 (additive model) GCV 0.3877448 RSS 312.877 GRSq 0.907529 RSq 0.9213739
Étant donné que ce modèle dans l'implémentation interne utilise la méthode GCV pour sélectionner un modèle, sa structure est quelque peu différente du modèle décrit précédemment dans ce chapitre. La méthode récapitulative génère une sortie plus étendue:
> summary(marsFit) Call: earth(x=solTrainXtrans, y=solTrainY) coefficients (Intercept) -3.223749 FP002 0.517848 FP003 -0.228759 FP059 -0.582140 FP065 -0.273844 FP075 0.285520 FP083 -0.629746 FP085 -0.235622 FP099 0.325018 FP111 -0.403920 FP135 0.394901 FP142 0.407264 FP154 -0.620757 FP172 -0.514016 FP176 0.308482 FP188 0.425123 FP202 0.302688 FP204 -0.311739 FP207 0.457080 h(MolWeight-5.77508) -1.801853 h(5.94516-MolWeight) 0.813322 h(NumNonHAtoms-2.99573) -3.247622 h(2.99573-NumNonHAtoms) 2.520305 h(2.57858-NumNonHBonds) -0.564690 h(NumMultBonds-1.85275) -0.370480 h(NumRotBonds-2.19722) -2.753687 h(2.19722-NumRotBonds) 0.123978 h(NumAromaticBonds-2.48491) -1.453716 h(NumNitrogen-0.584815) 8.239716 h(0.584815-NumNitrogen) -1.542868 h(NumOxygen-1.38629) 3.304643 h(1.38629-NumOxygen) -0.620413 h(NumChlorine-0.46875) -50.431489 h(HydrophilicFactor- -0.816625) 0.237565 h(-0.816625-HydrophilicFactor) -0.370998 h(SurfaceArea1-1.9554) 0.149166 h(SurfaceArea2-4.66178) -0.169960 h(4.66178-SurfaceArea2) -0.157970 Selected 38 of 47 terms, and 30 of 228 predictors Importance: NumNonHAtoms, MolWeight, SurfaceArea2, SurfaceArea1, FP142, ... Number of terms at each degree of interaction: 1 37 (additive model) GCV 0.3877448 RSS 312.877 GRSq 0.907529 RSq 0.9213739
Dans cette dérivation, h (·) est la fonction charnière. Dans les résultats ci-dessus, le composant h (MolWeight-5.77508) est égal à zéro pour un poids moléculaire inférieur à 5,77508 (comme dans la partie supérieure de la figure 7.3). La fonction de charnière réfléchie a la forme h (5.77508 - MolWeight).
La fonction plotmo du paquet terre peut être utilisée pour construire des diagrammes similaires à ceux montrés dans la fig. 7.5. Vous pouvez utiliser train pour configurer le modèle à l'aide d'un rééchantillonnage externe. Le code suivant reproduit les résultats montrés dans la fig. 7.4:
> # - > marsGrid <- expand.grid(.degree = 1:2, .nprune = 2:38) > # > set.seed(100) > marsTuned <- train(solTrainXtrans, solTrainY, + method = "earth", + # - + tuneGrid = marsGrid, + trControl = trainControl(method = "cv")) > marsTuned 951 samples 228 predictors No pre-processing Resampling: Cross-Validation (10-fold) Summary of sample sizes: 856, 857, 855, 856, 856, 855, ... Resampling results across tuning parameters: degree nprune RMSE Rsquared RMSE SD Rsquared SD 1 2 1.54 0.438 0.128 0.0802 1 3 1.12 0.7 0.0968 0.0647 1 4 1.06 0.73 0.0849 0.0594 1 5 1.02 0.75 0.102 0.0551 1 6 0.984 0.768 0.0733 0.042 1 7 0.919 0.796 0.0657 0.0432 1 8 0.862 0.821 0.0418 0.0237 : : : : : : 2 33 0.701 0.883 0.068 0.0307 2 34 0.702 0.883 0.0699 0.0307 2 35 0.696 0.885 0.0746 0.0315 2 36 0.687 0.887 0.0604 0.0281 2 37 0.696 0.885 0.0689 0.0291 2 38 0.686 0.887 0.0626 0.029 RMSE was used to select the optimal model using the smallest value. The final values used for the model were degree = 1 and nprune = 38. > head(predict(marsTuned, solTestXtrans)) [1] 0.3677522 -0.1503220 -0.5051844 0.5398116 -0.4792718 0.7377222
Deux fonctions sont utilisées pour évaluer l'importance de chaque prédicteur dans le modèle MARS: evimp du paquet terre et varImp du paquet caret (le second appelle le premier):
> varImp(marsTuned) earth variable importance only 20 most important variables shown (out of 228) Overall MolWeight 100.00 NumNonHAtoms 89.96 SurfaceArea2 89.51 SurfaceArea1 57.34 FP142 44.31 FP002 39.23 NumMultBond s 39.23 FP204 37.10 FP172 34.96 NumOxygen 30.70 NumNitrogen 29.12 FP083 28.21 NumNonHBonds 26.58 FP059 24.76 FP135 23.51 FP154 21.20 FP207 19.05 FP202 17.92 NumRotBonds 16.94 FP085 16.02
Ces résultats sont échelonnés dans une plage de 0 à 100, différents de ceux donnés dans le tableau. 7.1 (le modèle présenté dans le tableau 7.1 n'a pas suivi le processus complet de croissance et de troncature). Notez que les variables qui suivent les premières d'entre elles sont moins significatives pour le modèle.
SVM, méthode de vecteur de support
Les implémentations des modèles SVM sont contenues dans plusieurs packages R. Chang et Lin (Chang et Lin, 2011) utilisent la fonction svm du package e1071 pour utiliser l'interface de la bibliothèque LIBSVM pour la régression. Une implémentation plus complète des modèles SVM pour la régression de Karatsogl (Karatzoglou et al., 2004) est contenue dans le package kernlab, qui inclut la fonction ksvm pour les modèles de régression et un grand nombre de fonctions nucléaires. Par défaut, la fonction de base radiale est utilisée. Si les valeurs du coût et des paramètres nucléaires sont connues, l'approximation du modèle peut être effectuée comme suit:
> svmFit <- ksvm(x = solTrainXtrans, y = solTrainY, + kernel ="rbfdot", kpar = "automatic", + C = 1, epsilon = 0.1)
Pour estimer σ, une analyse automatisée a été utilisée. Puisque y est un vecteur numérique, la fonction se rapproche évidemment du modèle de régression (au lieu du modèle de classification). Vous pouvez utiliser d'autres fonctions du noyau, notamment polynomiale (kernel = "polydot") et linéaire (kernel = "vanilladot").
Si les valeurs sont inconnues, elles peuvent être estimées par rééchantillonnage. En train, les valeurs de "svmRadial", "svmLinear" ou "svmPoly" du paramètre de méthode sélectionnent différentes fonctions du noyau:
> svmRTuned <- train(solTrainXtrans, solTrainY, + method = "svmRadial", + preProc = c("center", "scale"), + tuneLength = 14, + trControl = trainControl(method = "cv"))
L'argument tuneLength utilise 14 valeurs par défaut.

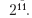
Une estimation par défaut de σ est effectuée par analyse automatique.
> svmRTuned 951 samples 228 predictors Pre-processing: centered, scaled Resampling: Cross-Validation (10-fold) Summary of sample sizes: 855, 858, 856, 855, 855, 856, ... Resampling results across tuning parameters: C RMSE Rsquared RMSE SD Rsquared SD 0.25 0.793 0.87 0.105 0.0396 0.5 0.708 0.889 0.0936 0.0345 1 0.664 0.898 0.0834 0.0306 2 0.642 0.903 0.0725 0.0277 4 0.629 0.906 0.067 0.0253 8 0.621 0.908 0.0634 0.0238 16 0.617 0.909 0.0602 0.0232 32 0.613 0.91 0.06 0.0234 64 0.611 0.911 0.0586 0.0231 128 0.609 0.911 0.0561 0.0223 256 0.609 0.911 0.056 0.0224 512 0.61 0.911 0.0563 0.0226 1020 0.613 0.91 0.0563 0.023 2050 0.618 0.909 0.0541 0.023 Tuning parameter 'sigma' was held constant at a value of 0.00387 RMSE was used to select the optimal model using the smallest value. The final values used for the model were C = 256 and sigma = 0.00387.
Le sous-objet finalModel contient le modèle créé par la fonction ksvm:
> svmRTuned$finalModel Support Vector Machine object of class "ksvm" SV type: eps-svr (regression) parameter : epsilon = 0.1 cost C = 256 Gaussian Radial Basis kernel function. Hyperparameter : sigma = 0.00387037424967707 Number of Support Vectors : 625 Objective Function Value : -1020.558 Training error : 0.009163
En tant que vecteurs de référence, le modèle utilise 625 points de données de l'ensemble d'apprentissage (soit 66% de l'ensemble d'apprentissage).
Le package kernlab contient une implémentation du modèle RVM pour la régression dans la fonction rvm. Sa syntaxe est très similaire à celle présentée dans l'exemple de ksvm.
Méthode KNN
Le paquet caren knnreg se rapproche du modèle de régression KNN; la fonction train définit le modèle sur K:
> # . > knnDescr <- solTrainXtrans[, -nearZeroVar(solTrainXtrans)] > set.seed(100) > knnTune <- train(knnDescr, + solTrainY, + method = "knn", + # + # + preProc = c("center", "scale"), + tuneGrid = data.frame(.k = 1:20), + trControl = trainControl(method = "cv"))
À propos des auteurs:
Max Kun est le chef du département de recherche et développement statistique non clinique de Pfizer Global. Il travaille avec des modèles prédictifs depuis plus de 15 ans et est l'auteur de plusieurs packages spécialisés pour le langage R. La modélisation prédictive dans la pratique couvre tous les aspects de la prévision, en commençant par les étapes clés du prétraitement des données, le fractionnement des données et les principes de base.
paramètres du modèle. Toutes les étapes de la modélisation sont considérées sur des exemples pratiques.
de la vie réelle, chaque chapitre donne un code détaillé en R.
Kjell Johnson travaille dans le domaine des statistiques et de la modélisation prédictive pour la recherche pharmaceutique depuis plus de dix ans. Co-fondateur d'Arbor Analytics, une entreprise spécialisée dans la modélisation prédictive; précédemment dirigé le département de recherche et développement statistique chez Pfizer Global. Son travail scientifique est consacré à l'application et au développement de méthodologies statistiques et d'algorithmes d'apprentissage.
»Plus d'informations sur le livre sont disponibles sur
le site Web de l'éditeur»
Contenu»
Extrait25% de réduction sur les colporteurs -
Modélisation prédictive appliquéeLors du paiement de la version papier du livre, un livre électronique est envoyé par e-mail.