Dans la première
publication, il a été dit qu'il existe un théorème Erd -s-Renyi oublié, dont il résulte que dans une série aléatoire de longueur N, avec une probabilité proche de 1, il existe une ligne de valeurs identiques de longueur
. La propriété indiquée d'une variable aléatoire peut être utilisée pour répondre à la question: "Après le traitement des mégadonnées, la série résiduelle obéit-elle ou non à la loi des nombres aléatoires?"
La réponse à cette question n'a pas été déterminée sur la base de tests de correspondance à la normalité de distribution, mais sur la base des propriétés de la série résiduelle elle-même.
Par la présence ou l'absence ou le décalage de la fréquence des contrats des mêmes personnages. J'ai essayé de publier, de montrer les possibilités d'utilisation de cet outil, bien que de nombreuses questions se soient posées sur la façon dont cela fonctionne dans la réalité lors de la réalisation d'analyses en big data. Mais la discussion a été productive et l'utilisateur de
VDG a même présenté un exemple réel:
«... Les branches dendritiques d'un neurone peuvent être représentées comme une séquence de bits. Une branche, puis le neurone entier, est déclenchée lorsqu'une chaîne de synapses est activée à n'importe quel endroit. Le neurone a pour tâche de ne pas répondre au bruit blanc, respectivement, la longueur minimale de la chaîne, pour autant que je m'en souvienne avec Numenty, est de 14 synapses dans le neurone pyramidal avec ses 10 mille synapses. Et selon la formule on obtient: . Autrement dit, des chaînes de moins de 14 longueurs se produiront en raison du bruit naturel, mais n'activeront pas le neurone. C'est parfaitement bien .
"Essayons de considérer le mécanisme présenté dans ce document.
La première publication a soulevé de nombreuses questions. Essayons de clarifier le mécanisme du théorème Erds-Renyi dans cet article.
La solution est apparue en lien avec le paradoxe du
Penny Game . Le jeu se compose des éléments suivants - deux joueurs A et B vont lancer une pièce cinq fois, en affectant, par exemple, "aigle" - 1, "queues" - 0. Le joueur A choisit une séquence de trois valeurs et l'exprime, supposons 001.
Le joueur B choisit sa séquence, supposons 100. Le joueur dont la séquence tombe en premier est le gagnant. Supposons que 01001 soit tombé, c'est-à-dire 0-100-1, ce qui correspond au choix de B. Le paradoxe du "Penny Game" est que quelle que soit la séquence choisie par un joueur A, le joueur B a toujours la possibilité de choisir une séquence dont la probabilité est plus grande que la séquence choisie par le joueur A. La matrice gagnante du joueur B est illustrée à la figure 1.
Fig. 1. La matrice de gains pour le joueur B dans le "Penny Game" pour cinq coups.L'effet de ce paradoxe est que la série aléatoire n'est pas transitive, c'est-à-dire que si U> R et R> Q, cela ne signifie pas que Q> U.
La conséquence de ce paradoxe est les choses ordinaires suivantes, si un joueur respecte les règles et se conforme aux lois de la théorie des probabilités:
- Dans le jeu, il gagne généralement, dont le caissier est plus - «écraser la banque».
- Dans un casino, seul le casino gagne.
- Lorsque vous jouez en bourse, seule la chance détermine la durée de vie d'un trader jusqu'à ce qu'il perde son capital.
La signification physique de cette loi, sur laquelle se fonde le paradoxe du «Penny Game», est que celui qui peut continuer le plus la séquence aléatoire a l'avantage. Comme dans le premier exemple - un joueur qui a plus d'argent. Dans la deuxième option - le casino joue avec des centaines de séquences en même temps et continuera à jouer après que l'un des joueurs ait arrêté le jeu. Un match contre l'échange d'un joueur ne se compare pas, avec des millions d'opérations sur l'échange.
Comme vous pouvez le voir, la première loi a été établie - BigData détermine la situation par rapport aux informations locales.
Le deuxième moment déterminant est l'absence de la propriété de transitivité des séquences aléatoires. La conséquence en est l'incapacité à faire reculer la situation.
Hypothèse supplémentaire dans l'analyse de BigData:
1) La compréhension de l'évolution des événements n'est possible que sur un tel volume dans lequel les conséquences des événements sous enquête sont enregistrées. Le mécanisme de ce processus peut être représenté comme suit. Un champ aléatoire est un champ dans lequel plusieurs processus potentiels tentent de se réaliser. Après la réalisation de soi, le processus laisse des changements, et nous essayons de détecter le degré de traces des processus qui se sont produits. Les dépendances sont déjà déterminées par l'ampleur de la part des résultats de gauche. J'expliquerai à ce qui précède qu'à mon avis, la façon dont les transformations elles-mêmes se produisent, à l'heure actuelle, la science ne peut pas donner une définition formelle. Si ces définitions l'étaient, alors certains des paradoxes de Zeno cesseraient d'être des paradoxes, et l'unité et la lutte des contraires, la dialectique matérialiste cesserait d'être un postulat.
Je suppose que vous ne devez pas briser les lances des déclarations selon lesquelles si nous déterminons le processus après coup, alors c'est un exercice dénué de sens, car le prochain processus sera imprévisible. Une personne voit assez localement, et les processus BigData peuvent durer des milliards d'années, nous avons donc la possibilité de voir le mécanisme d'un processus à partir du champ BigData. Des informations intéressantes sur les grandes valeurs de l'univers sont présentées
ici .
2) La deuxième hypothèse, qui peut être déduite de l'absence de la propriété de transitivité, est l'influence de l'intervalle et des conditions sur le processus étudié. C'est-à-dire, d'une part, qu'il y a une coordonnée temporelle qui positionne le processus à l'étude, et une chance de répéter les conditions dans lesquelles notre processus a été formé, et des millions d'enregistrements ont été reçus, est presque impossible. En revanche, les lois de la combinatoire ne peuvent être ignorées. Ces lois nous disent que la probabilité qu'une certaine combinaison se produise doit toujours exister. La figure 2 montre la distribution des variantes de chaînes de N signaux dans lesquelles il existe des rangées de sous-ordres de longueur k. Le montant total est supérieur à
, car les chaînes courtes sont combinées avec des chaînes plus longues.
Fig. 2. Le nombre de variantes de sous-ordre possibles de k signaux identiques, dans une séquence de N valeurs.Pour les variantes dans lesquelles des chaînes plus longues que N / 2 sont présentes, elles sont remplies en jaune, leur nombre est déterminé de manière assez simple par la formule:
Autrement dit, les probabilités correspondantes pour les séries contenant des chaînes de k> = N / 2 valeurs identiques (nous ne décrirons pas la probabilité d'une série de N valeurs) seront déterminées par la formule:
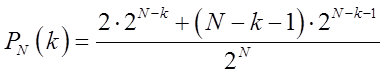
Au cours de la discussion, dans la première partie, des questions se sont posées, dont l'essence se résumait à ce qui suit: "Où sont les limites du bruit blanc?" Ici, en considérant le tableau de la figure 2, une hypothèse a été formulée pour discussion, selon le schéma suivant.
Basé sur le théorème intégral de Muavre-Laplace:
Nous définissons les intervalles pour f (1,96) = 95% de probabilité:
Si vous regardez, le tableau de la figure 2 reflète le champ complet des probabilités, d'autre part, les paramètres de distribution dans chaque cas sont définis de manière unique et sont présentés dans la figure 3, où nous les montrons comme un exemple d'une série de 9 valeurs. Depuis le nombre d'options
, et pour ce nombre de tests, nous trouverons alpha.
Fig. 3. Les limites des intervalles de probabilité des sous-ordres de longueur k des mêmes signaux, dans une séquence de 9 valeurs, avec une fiabilité de 2 sigma (95%).La figure 4 présente les intervalles pour une variable aléatoire, où la figure 4b est la figure 4a transposée.
Fig. 4. Intervalles de taille aléatoire pour chaque sous-ordre, avec une fiabilité de 95%.Afin de structurer en quelque sorte les réponses aux questions de savoir où se trouve le bruit blanc, il a formulé les approches existantes comme suit:
- Le bruit blanc est reconnu par la communauté;
- Données pouvant être formulées avec des expressions analytiques;
- Information structurée par des réseaux de neurones;
- Qubits, ordinateurs quantiques;
- BigData
- S'il existe des mégadonnées, il est tout à fait possible que des hyperdonnées existent.
Pour la structuration proposée, l'indice était l'idée d'O. V. Filatov
«Définition d'une séquence binaire aléatoire comme objet combinatoire. Calcul de fragments coïncidents dans des séquences binaires aléatoires » sur le comportement des fragments d'une séquence ressemblant au comportement des particules dans le micromonde.
Les qubits, qui ont une structure tridimensionnelle, donnent à penser que le schéma structurel devrait avoir un modèle tridimensionnel. Plusieurs couches, reconnues par la communauté, impliquaient la superposition du modèle et, combinant tout cela, le schéma le plus élégant est possible sous la forme d'un tore, figure 5.
Fig. 5. L'hypothèse de la structure des données dans la cartographie des variables aléatoires sur l'espace (images prises d'Internet).En développant le raisonnement plus loin, nous notons que sur la figure 3, toutes les fréquences sont des nombres pairs. Ceci est une conséquence de la symétrie des données "0-1". La symétrie des données aléatoires se reflète dans
les postulats du Golomb de Solomon Wolf Golomb . Basé sur la recherche Filatova O.V.
«Dérivation de formules pour les postulats de Golomb. Une façon de créer une séquence pseudo-aléatoire à partir des fréquences Mises. Les bases de la «combinatoire des séquences longues» utilisent le concept d'une demi-onde. Je pense que cet aspect est important dans l'étude du bruit blanc, car il est associé à des paramètres tels que la longueur de ligne.
Compte tenu des propriétés des processus aléatoires, une onde de bruit blanche peut acquérir diverses propriétés, notamment le manque
de symétrie des ondes et la non-conformité possible avec
le théorème de Noether . Mais il y a des processus dans le monde physique comme la formation de mousse d'une vague de surf, figure 6. Nous avons donc toutes les raisons d'autoriser des paramètres inhabituels de vagues de bruit blanc.
Fig. 6. Le mécanisme de déformation des vagues près de la côte et des exemples de processus qui, lorsqu'ils sont projetés sur certains hyperplans, dans l'espace local, peuvent ressembler à un processus aléatoire (photos prises sur Internet).Passant à la partie pratique, je résumerai les approches proposées lorsque l'on travaille avec du bruit blanc.
- Manque de propriété de transitivité dans les processus aléatoires.
- L'hypothèse selon laquelle les propriétés de symétrie dans le bruit blanc sont la réalisation des propriétés de symétrie des processus supérieurs aux processus dans la situation actuelle considérée.
- Localité des processus aléatoires. Cette prémisse n'est pas explicitement montrée dans la publication, mais s'intègre assez bien dans le cadre des mathématiques constructives. Vous l'utilisez tous (mathématiques constructives) lorsque vous écrivez un script qui définit la nécessité d'accéder à une cellule mémoire et de lire son contenu. Puisque par défaut vous voulez dire que dans cette cellule il y a une certaine valeur 0 ou 1 et rien d'autre ne peut y être. Un bon matériel pour vous familiariser avec ses approches est présenté ici: N.N. Nepeyvoda "Mathématiques constructives: un examen des réalisations, des faiblesses et des leçons. Partie I " .
Partie pratique
Dans la première partie, la question du théorème Erds-Renyi a été examinée, qui consistait dans le fait que ce théorème n'a été trouvé que dans une seule source, qui est traduite du hongrois, ce livre a été publié en URSS et aucune preuve ni mention n'a été trouvée . De ce fait, il existait une incertitude générale sur son existence et, surtout, sur son application.
À la suite de recherches, il a été découvert dans les travaux de Filatov O.V.
«Dérivation de formules pour les postulats de Golomb. Une façon de créer une séquence pseudo-aléatoire à partir des fréquences Mises. Les bases de la «Combinatoire des séquences longues» p. 15 ce qui suit, figure 7, je cite l'original du matériel.
Fig. 7. La partie originale de la publication Filatova OV «Dérivation de formules pour les postulats de Golomb. Une façon de créer une séquence pseudo-aléatoire à partir des fréquences Mises. Fondements de la «Combinatoire des séquences longues».Le théorème d'Erds-Renyi est formulé comme suit:
Lorsque vous lancez une pièce N fois, une série de côtés égaux tombants d'une pièce dans une rangée de longueur
observée avec une probabilité tendant vers 1, avec N tendant vers l'infini.
Nous écrivons le théorème dans les formulations «Combinatoire des séquences longues» pour un côté de la médaille:
Nous réalisons la preuve:
Comme vous pouvez le voir les fréquences Mises pour un train composé d'une chaîne de signaux identiques de longueur
coïncident avec les conclusions du théorème d'Erdos-Renyi sur la probabilité de la même chaîne dans le cas d'une série aléatoire. Ainsi, vous pouvez éliminer le doute et reconnaître son existence et la possibilité d'application.
Comme la publication était déjà plus recommandée par les marketeurs, la suite dans la partie suivante, «Le bruit blanc dessine un carré noir. Partie 3. Application. "
Autres parties:
partie 1 ,
partie 3 .