Dans le dernier chapitre, nous avons appris que les réseaux de neurones profonds (GNS) sont souvent plus difficiles à former que les réseaux peu profonds. Et c'est mauvais, car nous avons toutes les raisons de croire que si nous pouvions former les STS, ils seraient bien meilleurs pour accomplir les tâches. Mais alors que les nouvelles du chapitre précédent sont décevantes, cela ne nous arrêtera pas. Dans ce chapitre, nous développerons des techniques que nous pouvons utiliser pour former des réseaux profonds et les mettre en pratique. Nous examinerons également la situation plus largement, nous nous familiariserons brièvement avec les progrès récents dans l'utilisation de GNS pour la reconnaissance d'images, la parole et pour d'autres applications. Et considérez également superficiellement l'avenir des réseaux de neurones et de l'IA.
Ce sera un long chapitre, alors revenons un peu sur la table des matières. Ses sections ne sont pas fortement interconnectées.Par conséquent, si vous avez des concepts de base sur les réseaux de neurones, vous pouvez commencer par la section qui vous intéresse le plus.
La partie principale du chapitre est une introduction à l'un des types de réseaux profonds les plus populaires: les réseaux à convolution profonde (GSS). Nous travaillerons avec un exemple détaillé de l'utilisation d'un réseau de convolution, avec un code et d'autres choses, pour résoudre le problème de la classification des chiffres manuscrits de l'ensemble de données MNIST:
Nous commençons notre examen des réseaux convolutionnels par des réseaux peu profonds, que nous avons utilisés pour résoudre ce problème plus tôt dans le livre. En plusieurs étapes, nous créerons des réseaux de plus en plus puissants. En cours de route, nous découvrirons de nombreuses technologies puissantes: convolutions, mise en commun, utilisation de GPU pour augmenter considérablement la quantité de formation par rapport à ce que nous avons fait avec des réseaux peu profonds, expansion algorithmique des données de formation (pour réduire le sur-ajustement), utilisation de la technologie d'abandon (également pour réduire le recyclage), en utilisant des ensembles de réseaux et autres. En conséquence, nous arriverons à un système dont les capacités sont presque au niveau humain. Sur les 10 000 images de vérification du MNIST - que le système n'a pas vues pendant la formation - il pourra reconnaître correctement 9967. Et voici certaines de ces images qui n'ont pas été reconnues correctement. Dans le coin supérieur droit se trouvent les bonnes options; ce que notre programme a montré est indiqué dans le coin inférieur droit.
Beaucoup d'entre eux sont difficiles à classer chez l'homme. Prenez, par exemple, le troisième chiffre de la ligne supérieure. Cela me semble plus «9» que la version officielle de «8». Notre réseau a également décidé qu'il était "9". Au moins, de telles erreurs peuvent être pleinement comprises, et peut-être même approuvées. Nous concluons notre discussion sur la reconnaissance d'image par un aperçu des progrès considérables réalisés récemment par le réseau de neurones (en particulier les réseaux convolutifs).
Le reste du chapitre est consacré à une discussion sur l'apprentissage en profondeur d'un point de vue plus large et moins détaillé. Nous examinerons brièvement d'autres modèles de NS, en particulier les NS récurrents et les unités de mémoire à court terme à long terme, et comment ces modèles peuvent être utilisés pour résoudre des problèmes de reconnaissance vocale, de traitement du langage naturel, etc. Nous discuterons de l'avenir de la NS et de la protection civile, des idées telles que les interfaces utilisateur axées sur l'intention au rôle de l'apprentissage en profondeur dans l'IA.
Ce chapitre est basé sur le matériel des chapitres précédents du livre, en utilisant et en intégrant des idées telles que la rétropropagation, la régularisation, le softmax, etc. Cependant, pour lire ce chapitre, il n'est pas nécessaire de développer le contenu de tous les chapitres précédents. Cependant, cela ne fait pas de mal de lire le
chapitre 1 et d'apprendre les rudiments de l'Assemblée nationale. Lorsque j'utiliserai les concepts des chapitres 2 à 5, je donnerai les liens nécessaires vers le matériel si nécessaire.
Il convient de noter que ce chapitre ne le fait pas. Ce n'est pas du matériel de formation sur les bibliothèques les plus récentes et les plus cool pour travailler avec NS. Nous n'allons pas former STS avec des dizaines de couches pour résoudre des problèmes à la pointe de la recherche. Nous allons essayer de comprendre certains des principes de base qui sous-tendent GNS et les appliquer au contexte simple et facile à comprendre des tâches MNIST. En d'autres termes, ce chapitre ne vous mènera pas à l'avant-garde de la région. Le désir de ce chapitre et des chapitres précédents est de se concentrer sur les bases et de vous préparer à comprendre un large éventail d'œuvres contemporaines.
Introduction aux réseaux de neurones convolutifs
Dans les chapitres précédents, nous avons appris à nos réseaux de neurones qu'il est assez bon de reconnaître des images de nombres manuscrits:
Nous l'avons fait en utilisant des réseaux dans lesquels les couches voisines étaient complètement connectées les unes aux autres. C'est-à-dire que chaque neurone du réseau était associé à chaque neurone de la couche voisine:
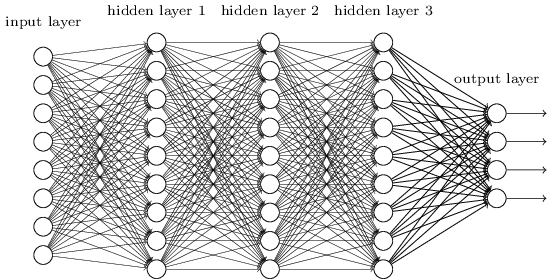
En particulier, nous avons codé l'intensité de chaque pixel de l'image comme valeur pour le neurone correspondant de la couche d'entrée. Pour les images de 28 x 28 pixels, cela signifie que le réseau aura 784 (= 28 × 28) neurones entrants. Ensuite, nous avons formé les poids et les décalages du réseau afin que la sortie (il y avait un tel espoir) identifie correctement l'image entrante: '0', '1', '2', ..., '8' ou '9'.
Nos premiers réseaux fonctionnent plutôt bien: nous avons atteint une précision de classification supérieure à 98% en utilisant des données de formation et de test à partir des chiffres manuscrits du MNIST. Mais si vous évaluez cette situation maintenant, il semble étrange d'utiliser un réseau avec des couches entièrement connectées pour classer les images. Le fait est qu'un tel réseau ne prend pas en compte la structure spatiale des images. Par exemple, il s'applique exactement de la même manière aux pixels situés loin les uns des autres, ainsi qu'aux pixels voisins. On suppose que des conclusions sur de tels concepts de structure spatiale devraient être tirées sur la base de l'étude des données d'entraînement. Mais que se passe-t-il si, au lieu de démarrer la structure du réseau à partir de zéro, nous utiliserons une architecture essayant de tirer parti de la structure spatiale? Dans cette section, je décris les réseaux de neurones convolutifs (SNA). Ils utilisent une architecture spéciale, particulièrement adaptée à la classification des images. Grâce à l'utilisation d'une telle architecture, les SNA apprennent plus rapidement. Et cela nous aide à former des réseaux plus profonds et plus stratifiés qui font un bon travail de classification des images. Aujourd'hui, le SNA profond ou une variante similaire est utilisé dans la plupart des cas de reconnaissance d'image.
Les origines du SCN remontent aux années 1970. Mais le travail de départ, qui a commencé leur distribution moderne, était le travail de 1998, "
Gradient Learning for Recognizing Documents ." Lekun a fait une
remarque intéressante sur la terminologie utilisée dans le SCN: «La connexion de modèles tels que les réseaux convolutifs avec la neurobiologie est très superficielle. Par conséquent, je les appelle des réseaux convolutifs, pas des réseaux de neurones convolutifs, et donc nous appelons leurs éléments nœuds, pas des neurones. " Mais, malgré cela, le SNA utilise de nombreuses idées du monde NS que nous avons déjà étudiées: rétropropagation, descente de gradient, régularisation, fonctions d'activation non linéaires, etc. Par conséquent, nous suivrons l'accord généralement accepté et les considérerons comme une sorte d'AN. Je les appellerai à la fois réseaux et réseaux de neurones, et leurs nœuds - à la fois neurones et éléments.
Le SCN utilise trois idées de base: champs récepteurs locaux, poids totaux et mise en commun. Examinons tour à tour ces idées.
Champs récepteurs locaux
Dans les couches de réseau entièrement connectées, les couches d'entrée sont indiquées par des lignes verticales de neurones. Dans le SNA, il est plus commode de représenter la couche d'entrée sous la forme d'un carré de neurones d'une dimension de 28x28, dont les valeurs correspondent aux intensités de pixels de l'image 28x28:
Comme d'habitude, nous associons les pixels entrants à une couche de neurones cachés. Cependant, nous n'associerons pas chaque pixel à chaque neurone caché. Nous organisons les communications dans de petites zones localisées de l'image entrante.
Plus précisément, chaque neurone de la première couche cachée sera associé à une petite partie des neurones entrants, par exemple une région 5x5 correspondant à 25 pixels entrants. Donc, pour certains neurones cachés, la connexion peut ressembler à ceci:
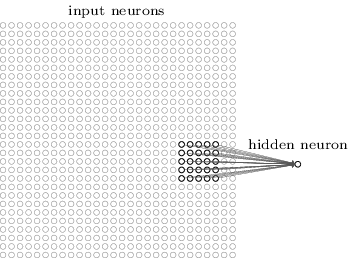
Cette partie de l'image entrante est appelée le champ récepteur local pour ce neurone caché. Il s'agit d'une petite fenêtre regardant les pixels entrants. Chaque lien apprend son poids. De plus, un neurone caché étudie le déplacement général. Nous pouvons supposer que ce neurone particulier apprend à analyser son champ récepteur local spécifique.
Ensuite, nous déplaçons le champ récepteur local tout au long de l'image entrante. Chaque champ récepteur local a son propre neurone caché dans la première couche cachée. Pour une illustration plus spécifique, commencez par le champ récepteur local dans le coin supérieur gauche:
Déplacez le champ récepteur local d'un pixel vers la droite (un neurone) pour l'associer au deuxième neurone caché:
Nous construisons donc la première couche cachée. Notez que si notre image entrante est 28x28 et que le champ récepteur local est 5x5, alors il y aura 24x24 neurones dans la couche cachée. En effet, nous ne pouvons déplacer le champ récepteur local que de 23 neurones vers la droite (ou vers le bas), puis nous rencontrerons le côté droit (ou le bas) de l'image entrante.
Dans cet exemple, les champs récepteurs locaux se déplacent d'un pixel à la fois. Mais parfois, une taille de pas différente est utilisée. Par exemple, nous pourrions déplacer le champ récepteur local de 2 pixels sur le côté, et dans ce cas, nous pouvons parler de la taille de l'étape 2. Dans ce chapitre, nous utiliserons principalement l'étape 1, mais vous devez savoir que parfois des expériences avec des étapes d'une taille différente sont effectuées . Vous pouvez expérimenter avec la taille du pas, comme avec d'autres hyperparamètres. Vous pouvez également modifier la taille du champ récepteur local, mais il s'avère généralement qu'une plus grande taille du champ récepteur local fonctionne mieux sur des images nettement supérieures à 28x28 pixels.
Poids et compensations totaux
J'ai mentionné que chaque neurone caché a un décalage et des poids 5x5 associés à son champ récepteur local. Mais je n'ai pas mentionné que nous utiliserons les mêmes poids et déplacements pour tous les neurones cachés 24x24. En d'autres termes, pour un neurone caché j, k, la sortie sera égale à:
Ici, σ est la fonction d'activation, peut-être un sigmoïde des chapitres précédents. b est la valeur de décalage totale. w
l, m - tableau de poids totaux 5x5. Et enfin, a
x, y désigne l'activation d'entrée à la position x, y.
Cela signifie que tous les neurones de la première couche cachée détectent le même signe, juste situé dans différentes parties de l'image. Un signe détecté par un neurone caché est une certaine séquence entrante conduisant à l'activation d'un neurone: peut-être le bord de l'image, ou une certaine forme. Pour comprendre pourquoi cela a du sens, supposons que nos poids et déplacements soient tels qu'un neurone caché puisse reconnaître, disons, une face verticale dans un champ récepteur local spécifique. Cette capacité est susceptible d'être utile ailleurs dans l'image. Par conséquent, il est utile d'utiliser le même détecteur de caractéristiques sur toute la zone d'image. Plus abstraitement, le SNA est bien adapté à l'invariance translationnelle des images: déplacez l'image, par exemple, du chat, un peu sur le côté, et elle restera toujours l'image du chat. Certes, les images du problème de classification des chiffres du MNIST sont toutes centrées et de taille normalisée. Par conséquent, MNIST a moins d'invariance translationnelle que les images aléatoires. Pourtant, des caractéristiques telles que les visages et les angles sont susceptibles d'être utiles sur toute la surface de l'image entrante.
Pour cette raison, nous appelons parfois le mappage d'une couche entrante et d'une couche cachée une carte d'entités. Les poids qui définissent la carte des caractéristiques, nous appelons les poids totaux. Et le biais définissant la carte des caractéristiques est le biais général. On dit souvent que le poids total et le déplacement déterminent un noyau ou un filtre. Mais dans la littérature, les gens utilisent parfois ces termes pour une raison légèrement différente, et donc je n'entrerai pas dans la terminologie; Mieux, regardons quelques exemples spécifiques.
La structure de réseau que j'ai décrite est capable de reconnaître uniquement un attribut localisé d'une espèce. Pour reconnaître les images, nous avons besoin de plus de cartes de fonctionnalités. Par conséquent, la couche convolutionnelle finie se compose de plusieurs cartes d'entités différentes:
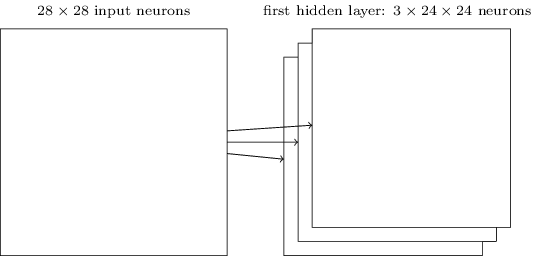
L'exemple montre 3 cartes d'entités. Chaque carte est déterminée par un ensemble de poids totaux 5x5 et un décalage commun. En conséquence, un tel réseau peut reconnaître trois types de signes différents, et chaque signe peut être trouvé dans n'importe quelle partie de l'image.
J'ai dessiné trois cartes attribut pour plus de simplicité. Dans la pratique, le SCN peut utiliser davantage de cartes d'entités (peut-être beaucoup plus). L'un des premiers SNS, LeNet-5, a utilisé 6 cartes de caractéristiques, chacune associée à un champ récepteur 5x5, pour reconnaître les chiffres du MNIST. Par conséquent, l'exemple ci-dessus est très similaire à LeNet-5. Dans les exemples que nous développerons de manière indépendante, nous utiliserons des couches convolutives contenant 20 et 40 cartes fonctionnelles. Jetons un coup d'œil aux signes que nous allons examiner:
Ces 20 images correspondent à 20 cartes d'attributs différentes (filtres ou noyaux). Chaque carte est représentée par une image 5x5 correspondant à 5x5 poids du champ récepteur local. Les pixels blancs signifient un poids faible (généralement plus négatif) et la carte des entités réagit moins aux pixels correspondants. Les pixels plus sombres signifient plus de poids et la carte des entités réagit davantage aux pixels correspondants. En gros, ces images montrent ces signes auxquels la couche convolutionnelle répond.
Quelles conclusions peut-on tirer de ces cartes d'attributs? Les structures spatiales ici, évidemment, ne sont pas apparues de manière aléatoire - de nombreux signes montrent des zones claires et sombres claires. Cela suggère que notre réseau apprend vraiment quelque chose lié aux structures spatiales. Cependant, outre cela, il est assez difficile de comprendre quels sont ces signes. Nous n'étudions évidemment pas, disons, les
filtres de Gabor , qui étaient utilisés dans de nombreuses approches traditionnelles de reconnaissance de formes. En fait, beaucoup de travail est en cours actuellement afin de mieux comprendre exactement quels signes sont étudiés par le SCN. Si vous êtes intéressé, je vous recommande de commencer avec
2013 .
Le grand avantage des poids et décalages généraux est que cela réduit considérablement le nombre de paramètres disponibles pour le SCN. Pour chaque carte d'entités, nous avons besoin de 5 × 5 = 25 poids totaux et d'un décalage commun. Par conséquent, 26 paramètres sont requis pour chaque carte d'entités. Si nous avons 20 cartes d'entités, alors au total, nous aurons 20 × 26 = 520 paramètres qui définissent la couche de convolution. À titre de comparaison, supposons que nous ayons une première couche entièrement connectée avec 28 × 28 = 784 neurones entrants et 30 neurones cachés relativement modestes - nous avons utilisé ce schéma dans de nombreux exemples plus tôt. Il s'avère que 784 × 30 poids, plus 30 décalages, un total de 23 550 paramètres. En d'autres termes, une couche entièrement connectée aura plus de 40 fois plus de paramètres qu'une couche convolutionnelle.
Bien sûr, nous ne pouvons pas comparer directement le nombre de paramètres, car ces deux modèles diffèrent radicalement. Mais intuitivement, il semble que l'utilisation de l'invariance translationnelle convolutionnelle réduit le nombre de paramètres nécessaires pour atteindre une efficacité comparable à celle d'un modèle entièrement connecté. Et cela, à son tour, accélérera la formation du modèle convolutionnel et, en fin de compte, nous aidera à créer des réseaux plus profonds à l'aide de couches convolutionnelles.
Soit dit en passant, le nom «convolutionnel» vient de l'opération dans l'équation (125), qui est parfois appelée
convolution . Plus précisément, les gens écrivent parfois cette équation sous la forme
1 = σ (b + w ∗ a
0 ), où
1 désigne un ensemble d'activations de sortie d'une carte de fonction, un
0 - un ensemble d'activations d'entrée et * est appelé une opération de convolution. Nous n'allons pas approfondir les mathématiques des convolutions, vous n'avez donc pas à vous soucier particulièrement de cette connexion.
Mais cela vaut juste la peine de savoir d'où vient le nom.Mise en commun des couches
Outre les couches convolutives décrites dans le SCN, il existe également des couches de mise en commun. Ils sont généralement utilisés immédiatement après la convolution. Ils se sont engagés à simplifier les informations de la sortie de la couche convolutionnelle.Ici, j'utilise l'expression «carte des caractéristiques» non pas dans le sens de la fonction calculée par la couche convolutionnelle, mais pour indiquer l'activation de la sortie des neurones de la couche cachée. Une telle utilisation gratuite des termes se retrouve souvent dans la littérature de recherche.La couche de mise en commun accepte la sortie de chaque carte d'entités de couche de convolution et prépare une carte d'entités compressée. Par exemple, chaque élément de la couche de regroupement peut résumer une section de, disons, 2x2 neurones de la couche précédente. Étude de cas: une procédure de mise en commun commune est connue sous le nom de mise en commun maximale. Dans le regroupement maximal, l'élément de regroupement donne simplement l'activation maximale à partir de la section 2x2, comme le montre le diagramme:
Étant donné que la sortie des neurones de la couche convolutionnelle donne des valeurs 24x24, après le regroupement, nous obtenons 12x12 neurones.Comme mentionné ci-dessus, une couche convolutionnelle implique généralement quelque chose de plus qu'une seule carte d'entités. Nous appliquons la mise en commun maximale à chaque carte d'entités individuellement. Donc, si nous avons trois cartes d'entités, les couches combinées de convolution et de regroupement maximal ressembleront à ceci: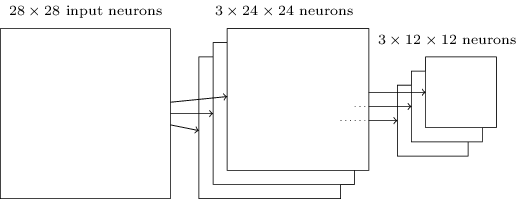
Le max-pulling peut être imaginé comme un moyen du réseau pour demander s'il y a un signe donné à n'importe quel endroit de l'image. Et puis elle jette des informations sur son emplacement exact. Il est intuitivement clair que lorsqu'un signe est trouvé, son emplacement exact n'est plus aussi important que son emplacement approximatif par rapport aux autres signes. L'avantage est que le nombre de fonctionnalités obtenues en utilisant le regroupement est beaucoup plus petit, ce qui contribue à réduire le nombre de paramètres requis dans les couches suivantes.La mise en commun maximale n'est pas la seule technologie de mise en commun. Une autre approche courante est connue sous le nom de pooling L2. Dans ce document, au lieu de prendre l'activation maximale de la région des neurones 2x2, nous prenons la racine carrée de la somme des carrés de l'activation de la région 2x2. Les détails des approches diffèrent, mais intuitivement, ils sont similaires à la mise en commun maximale: la mise en commun L2 est un moyen de compresser les informations d'une couche convolutionnelle. En pratique, les deux technologies sont souvent utilisées. Parfois, les gens utilisent d'autres types de mise en commun. Si vous avez du mal à optimiser la qualité du réseau, vous pouvez utiliser les données de prise en charge pour comparer plusieurs approches différentes de l'extraction et choisir la meilleure. Mais nous ne nous inquiéterons pas d'une optimisation aussi détaillée.Résumer
Nous pouvons maintenant rassembler toutes les informations et obtenir un SCN complet. Il est similaire à notre architecture récemment revue, mais il a une couche supplémentaire de 10 neurones de sortie correspondant à 10 valeurs possibles des chiffres MNIST ('0', '1', '2', ..):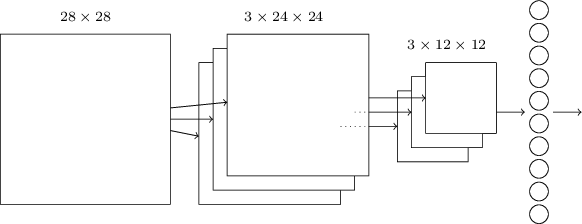
Le réseau démarre avec 28x28 neurones d'entrée utilisés pour coder l'intensité en pixels de l'image MNIST. Après cela vient une couche convolutionnelle utilisant des champs récepteurs locaux 5x5 et 3 cartes de caractéristiques. Le résultat est une couche de neurones à traits cachés de 3x24x24. L'étape suivante est une couche de regroupement maximale appliquée à des zones 2x2 sur chacune des trois cartes d'entités. Le résultat est une couche de neurones à traits cachés de 3x12x12.La dernière couche de connexions du réseau est entièrement connectée. Autrement dit, il connecte chaque neurone de la couche de regroupement maximale à chacun des 10 neurones de sortie. Nous avons utilisé une telle architecture entièrement connectée plus tôt. Veuillez noter que dans le diagramme ci-dessus, j'ai utilisé une seule flèche pour plus de simplicité, ne montrant pas tous les liens. Vous pouvez facilement les imaginer tous.Cette architecture convolutionnelle est très différente de ce que nous utilisions auparavant. Cependant, l'image globale est similaire: un réseau composé de nombreux éléments simples, dont le comportement est déterminé par des poids et des décalages. L'objectif reste le même: utiliser les données d'entraînement pour entraîner le réseau en poids et décalages afin que le réseau classe bien les numéros entrants.En particulier, comme dans les chapitres précédents, nous formerons notre réseau en utilisant la descente et la propagation de gradient stochastique. La procédure se déroule presque comme avant. Cependant, nous devons apporter quelques modifications à la procédure de rétropropagation. Le fait est que nos dérivés de rétropropagation étaient destinés à un réseau avec des couches entièrement connectées. Heureusement, la modification des dérivés pour les couches convolutionnelles et de regroupement maximal est assez simple. Si vous voulez comprendre les détails, je vous invite à essayer de résoudre le problème suivant. Je vous préviens que cela prendra beaucoup de temps, à moins que vous n'ayez bien compris les premières questions de différenciation de la rétropropagation.Défi
- . (BP1)-(BP4). , , - , . ?
Nous avons discuté des idées derrière le SCN. Voyons comment ils fonctionnent dans la pratique en mettant en œuvre certains SCN et en les appliquant au problème de classification des chiffres du MNIST. Nous utiliserons le programme network3.py, une version améliorée des programmes network.py et network2.py créés dans les chapitres précédents. Le programme network3.py utilise des idées de la documentation de la bibliothèque Theano (en particulier, l' implémentation LeNet-5 ), de l' implémentation de l'exception de Misha Denil et Chris Olah . Le code du programme est disponible sur GitHub. Dans la section suivante, nous étudierons le code du programme network3.py, et dans cette section, nous l'utiliserons comme bibliothèque pour créer le SNA.Les programmes network.py et network2.py ont été écrits en python à l'aide de la bibliothèque de matrices Numpy. Ils ont travaillé sur la base des premiers principes et ont atteint les détails les plus détaillés de la propagation arrière, de la descente de gradient stochastique, etc. Mais maintenant, quand nous comprendrons ces détails, pour network3.py, nous utiliserons la bibliothèque d'apprentissage automatique Theano (voir le travail scientifique avec sa description). Theano est également la base des bibliothèques populaires pour NS Pylearn2 et Keras , ainsi que Caffe et Torch .L'utilisation de Theano facilite la mise en œuvre de la rétropropagation dans le SCN, car il compte automatiquement toutes les cartes. Theano est également nettement plus rapide que notre code précédent (qui a été écrit pour faciliter la compréhension et non pour le travail à haute vitesse), il est donc raisonnable de l'utiliser pour former des réseaux plus complexes. En particulier, l'une des grandes fonctionnalités de Theano est d'exécuter du code sur le CPU et le GPU, si disponible. L'exécution sur un GPU offre une augmentation significative de la vitesse et aide à former des réseaux plus complexes.Pour travailler en parallèle avec le livre, vous devez installer Theano sur votre système. Pour ce faire, suivez les instructions sur la page d'accueil du projet. Au moment de la rédaction et du lancement des exemples, Theano 0.7 était disponible. J'ai effectué quelques expériences sur Mac OS X Yosemite sans GPU. Certains sur Ubuntu 14.04 avec un GPU NVIDIA. Et certains sont là, et là. Pour démarrer network3.py, définissez l'indicateur GPU dans le code sur True ou False. De plus, les instructions suivantes peuvent vous aider à exécuter Theano sur votre GPU . Il est également facile de trouver du matériel de formation en ligne. Si vous n'avez pas votre propre GPU, vous pouvez vous tourner vers Amazon Web Services EC2 G2. Mais même avec un GPU, notre code ne fonctionnera pas très rapidement. De nombreuses expériences passeront de quelques minutes à plusieurs heures. Le plus complexe d'entre eux sur un seul processeur sera exécuté pendant plusieurs jours. Comme dans les chapitres précédents, je recommande de commencer l'expérience et de continuer la lecture, en vérifiant périodiquement son fonctionnement. Sans utiliser de GPU, je vous recommande de réduire le nombre d'époques d'entraînement pour les expériences les plus complexes.Pour obtenir des résultats de base pour la comparaison, commençons par une architecture peu profonde avec une couche cachée contenant 100 neurones cachés. Nous étudierons 60 époques, utiliserons la vitesse d'apprentissage η = 0,1, la taille du mini-package est de 10, et nous étudierons sans régularisation.Dans cette section, j'ai défini un nombre spécifique d'époques de formation. Je le fais pour plus de clarté dans le processus d'apprentissage. En pratique, il est utile d'utiliser des arrêts précoces, de suivre la précision de l'ensemble de confirmation et d'arrêter la formation lorsque nous sommes convaincus que la précision de la confirmation ne s'améliore plus:>>> import network3 >>> from network3 import Network >>> from network3 import ConvPoolLayer, FullyConnectedLayer, SoftmaxLayer >>> training_data, validation_data, test_data = network3.load_data_shared() >>> mini_batch_size = 10 >>> net = Network([ FullyConnectedLayer(n_in=784, n_out=100), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(training_data, 60, mini_batch_size, 0.1, validation_data, test_data)
La meilleure précision de classification était de 97,80%. Il s'agit de la précision de classification test_data, estimée à partir de l'ère de la formation, dans laquelle nous avons obtenu la meilleure précision de classification pour les données de validation_data. L'utilisation de données de validation pour prendre une décision concernant l'évaluation de l'exactitude permet d'éviter de se recycler. Ensuite, nous le ferons. Vos résultats peuvent varier légèrement, car les pondérations et les décalages du réseau sont initialisés de manière aléatoire.
La précision de 97,80% est assez proche de la précision de 98,04% obtenue au chapitre 3, en utilisant une architecture de réseau similaire et des hyperparamètres d'entraînement. En particulier, les deux exemples utilisent des réseaux peu profonds avec une couche cachée contenant 100 neurones cachés. Les deux réseaux apprennent 60 époques avec une taille de mini-paquet de 10 et un taux d'apprentissage de η = 0,1.
Cependant, il y avait deux différences dans le réseau précédent. Premièrement, nous avons effectué une régularisation pour aider à réduire l'impact de la reconversion. La régularisation du réseau actuel améliore la précision, mais pas beaucoup, donc nous n'y penserons pas pour l'instant. Deuxièmement, bien que la dernière couche du premier réseau ait utilisé des activations sigmoïdes et la fonction de coût d'entropie croisée, le réseau actuel utilise la dernière couche avec softmax et la fonction de vraisemblance logarithmique comme fonction de coût. Comme décrit au chapitre 3, ce n'est pas un changement majeur. Je ne suis pas passé de l'un à l'autre pour une raison profonde - principalement parce que softmax et la fonction de vraisemblance logarithmique sont plus souvent utilisés dans les réseaux modernes pour classer les images.
Pouvons-nous améliorer les résultats en utilisant une architecture de réseau plus profonde?
Commençons par insérer une couche convolutive, au tout début du réseau. Nous utiliserons le champ récepteur local 5x5, une longueur de pas de 1 et 20 cartes fonctionnelles. Nous allons également insérer une couche de regroupement maximale combinant des fonctionnalités à l'aide de fenêtres de regroupement 2x2. Ainsi, l'architecture globale du réseau ressemblera à celle dont nous avons discuté dans la section précédente, mais avec une couche supplémentaire entièrement connectée:
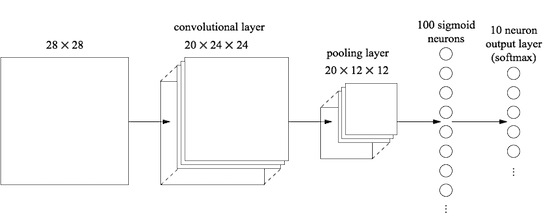
Dans cette architecture, les couches de convolution et de mise en commun sont entraînées dans la structure spatiale locale contenue dans l'image d'apprentissage entrante, et la dernière couche entièrement connectée est entraînée à un niveau plus abstrait, intégrant des informations globales de l'image entière. Il s'agit d'un schéma couramment utilisé dans le SCN.
Entraînons un tel réseau et voyons comment il se comporte.
>>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2)), FullyConnectedLayer(n_in=20*12*12, n_out=100), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(training_data, 60, mini_batch_size, 0.1, validation_data, test_data)
Nous obtenons une précision de 98,78%, ce qui est nettement supérieur à tous les résultats précédents. Nous avons réduit l'erreur de plus d'un tiers - un excellent résultat.
Décrivant la structure du réseau, j'ai considéré les couches convolutionnelles et de mise en commun comme une seule couche. Considérez-les comme des calques séparés ou comme un seul calque - une question de préférence. network3.py les considère comme une seule couche, car de cette façon, le code est plus compact. Cependant, il est facile de modifier network3.py afin que les couches puissent être définies individuellement.
Exercice
- Quelle précision de classification obtiendrons-nous si nous abaissons la couche entièrement connectée et utilisons uniquement la couche convolution / pool et la couche softmax? L'ajout d'une couche entièrement connectée est-il utile?
Pouvons-nous améliorer le résultat de 98,78%?
Essayons d'insérer la deuxième couche de convolution / pooling. Nous l'insérerons entre la convolution / pooling existante et les couches cachées entièrement connectées. Nous utilisons à nouveau le champ récepteur local 5x5 et le pool en sections 2x2. Voyons ce qui se passe lorsque nous formons un réseau avec approximativement les mêmes hyperparamètres qu'auparavant:
>>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2)), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2)), FullyConnectedLayer(n_in=40*4*4, n_out=100), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(training_data, 60, mini_batch_size, 0.1, validation_data, test_data)
Et encore une fois, nous avons une amélioration: nous obtenons maintenant une précision de 99,06%!
Pour le moment, deux questions naturelles se posent. Premièrement: que signifie utiliser la deuxième couche de convolution / pooling? Vous pouvez supposer qu'à la deuxième couche de convolution / regroupement, des images «12x12» arrivent à l'entrée, dont les «pixels» représentent la présence (ou l'absence) de certaines caractéristiques localisées dans l'image entrante d'origine. Autrement dit, nous pouvons supposer qu'une certaine version de l'image entrante d'origine arrive à l'entrée de cette couche. Ce sera une version plus abstraite et concise, mais elle a toujours suffisamment de structure spatiale, il est donc logique d'utiliser une deuxième couche de convolution / traction pour la traiter.
Un point de vue agréable, mais cela soulève une deuxième question. À la sortie de la couche précédente, 20 CP séparés sont obtenus, par conséquent, des groupes d'entrée 20x12x12 arrivent à la deuxième couche de convolution / regroupement. Il s'avère que nous avons, pour ainsi dire, 20 images distinctes incluses dans la couche convolution / pool, et non une image, comme ce fut le cas avec la première couche convolution / pool. Alors, comment les neurones de la deuxième couche de convolution / pool doivent-ils répondre à bon nombre de ces images entrantes? En fait, nous laissons simplement chaque neurone de cette couche apprendre sur la base de tous les neurones 20x5x5 entrant dans son champ récepteur local. Dans un langage moins formel, les détecteurs d'entités de la deuxième couche de convolution / pool auront accès à toutes les entités de la première couche, mais uniquement dans leurs champs récepteurs locaux spécifiques.
Soit dit en passant, un tel problème se serait posé dans la première couche, si les images étaient en couleur. Dans ce cas, nous aurions 3 attributs d'entrée pour chaque pixel correspondant aux canaux rouge, vert et bleu de l'image d'origine. Et ensuite, nous donnerions également aux détecteurs de signes accès à toutes les informations de couleur, mais uniquement dans le cadre de leur champ récepteur local.
Défi
- Utilisation de la fonction d'activation sous forme de tangente hyperbolique. Plus tôt dans ce livre, j'ai mentionné plusieurs fois la preuve que la fonction tanh, une tangente hyperbolique, pourrait être mieux adaptée pour être une fonction d'activation qu'une sigmoïde. Nous n'avons rien fait avec cela, car nous avons bien progressé avec le sigmoïde. Mais essayons quelques expériences avec tanh comme fonction d'activation. Essayez de former un réseau activé par tang avec des couches convolutionnelles et entièrement connectées (vous pouvez passer activation_fn = tanh comme paramètre aux classes ConvPoolLayer et FullyConnectedLayer). Commencez avec les mêmes hyperparamètres que le réseau sigmoïde, mais entraînez le réseau de 20 époques, pas 60. Comment se comporte le réseau? Que se passera-t-il si nous continuons jusqu'à la 60e ère? Essayez de construire un graphique de la précision de la confirmation du travail par les époques pour tangente et sigmoïde, jusqu'à la 60e ère. Si vos résultats sont similaires aux miens, vous constaterez que le réseau basé sur la tangente apprend un peu plus rapidement, mais la précision résultante des deux réseaux est la même. Pouvez-vous expliquer pourquoi cela se produit? Est-il possible d'atteindre la même vitesse d'apprentissage avec un sigmoïde - par exemple, en modifiant la vitesse d'apprentissage ou par mise à l'échelle (rappelez-vous que σ (z) = (1 + tanh (z / 2)) / 2)? Essayez cinq ou six hyperparamètres ou architectures de réseau différents, recherchez où la tangente peut être en avance sur le sigmoïde. Je note que cette tâche est ouverte. Personnellement, je n'ai trouvé aucun avantage sérieux à passer à la tangente, même si je n'ai pas mené d'expériences complètes, et peut-être les trouverez-vous. Dans tous les cas, nous trouverons bientôt un avantage à passer à une fonction d'activation linéaire redressée, nous ne nous attarderons donc plus sur la question de la tangente hyperbolique.
Utilisation d'éléments linéaires redressés
Le réseau que nous avons développé en ce moment est l'une des options de réseau utilisées dans le
travail fructueux de 1998 , dans lequel la tâche du MNIST, un réseau appelé LeNet-5, a été présentée pour la première fois. C'est une bonne base pour d'autres expériences, pour améliorer la compréhension du problème et l'intuition. En particulier, il existe de nombreuses façons dont nous pouvons changer notre réseau à la recherche de moyens d'améliorer les résultats.
Tout d'abord, changeons nos neurones afin qu'au lieu d'utiliser la fonction d'activation sigmoïde, nous puissions utiliser des éléments linéaires redressés (ReLU). Autrement dit, nous utiliserons la fonction d'activation de la forme f (z) ≡ max (0, z). Nous formerons un réseau de 60 époques, avec une vitesse de η = 0,03. J'ai également trouvé qu'il est un peu plus pratique d'utiliser la régularisation L2 avec le paramètre de régularisation λ = 0,1:
>>> from network3 import ReLU >>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2), activation_fn=ReLU), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2), activation_fn=ReLU), FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(training_data, 60, mini_batch_size, 0.03, validation_data, test_data, lmbda=0.1)
J'ai obtenu une précision de classification de 99,23%. Une amélioration modeste par rapport aux résultats sigmoïdes (99,06%). Cependant, dans toutes mes expériences, j'ai trouvé que les réseaux basés sur ReLU étaient en avance sur les réseaux basés sur la fonction d'activation sigmoïde avec une constance enviable. Apparemment, le passage à ReLU présente de réels avantages pour résoudre ce problème.
Qu'est-ce qui rend la fonction d'activation ReLU meilleure que la tangente sigmoïde ou hyperbolique? Pour le moment, nous ne comprenons pas particulièrement cela. On dit généralement que la fonction max (0, z) ne sature pas dans le grand z, contrairement aux neurones sigmoïdes, et cela aide les neurones ReLU à continuer à apprendre. Je ne discute pas, mais une telle excuse ne peut pas être qualifiée de complète, c'est juste une sorte d'observation (je vous rappelle que nous avons discuté de la saturation dans le
chapitre 2 ).
ReLU a commencé à être activement utilisé au cours des dernières années. Ils ont été adoptés pour des raisons empiriques: certaines personnes ont essayé ReLU, souvent simplement basé sur des intuitions ou des arguments heuristiques. Ils ont obtenu de bons résultats et la pratique s'est répandue. Dans un monde idéal, nous aurions une théorie nous disant quelles applications quelles fonctions d'activation sont les meilleures pour quelles applications. Mais pour l'instant, nous avons encore un long chemin à parcourir dans une telle situation. Je ne serai pas du tout surpris si de nouvelles améliorations dans le fonctionnement des réseaux peuvent être obtenues en choisissant une fonction d'activation encore plus appropriée. Je m'attends également à ce qu'une bonne théorie des fonctions d'activation soit développée dans les prochaines décennies. Mais aujourd'hui, nous devons nous appuyer sur des règles empiriques et une expérience peu étudiées.
Extension des données de formation
Une autre façon qui pourrait nous aider à améliorer nos résultats est d'étendre algorithmiquement les données d'entraînement. La manière la plus simple d'étendre les données d'entraînement est de décaler chaque image d'entraînement d'un pixel, vers le haut, le bas, la droite ou la gauche. Cela peut être fait en exécutant le programme
expand_mnist.py .
$ python expand_mnist.py
Le lancement du programme transforme 50 000 images de formation du MNIST en un ensemble élargi de 250 000 images de formation. Ensuite, nous pouvons utiliser ces images de formation pour former le réseau. Nous utiliserons le même réseau qu'auparavant avec ReLU. Dans mes premières expériences, j'ai réduit le nombre d'époques d'entraînement - c'était logique, car nous avons 5 fois plus de données d'entraînement. Cependant, l'extension de l'ensemble de données a considérablement réduit l'effet de la reconversion. Par conséquent, après avoir mené plusieurs expériences, je suis revenu au nombre d'époques 60. En tout cas, entraînons-nous:
>>> expanded_training_data, _, _ = network3.load_data_shared( "../data/mnist_expanded.pkl.gz") >>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2), activation_fn=ReLU), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2), activation_fn=ReLU), FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(expanded_training_data, 60, mini_batch_size, 0.03, validation_data, test_data, lmbda=0.1)
En utilisant des données d'entraînement avancées, j'ai obtenu une précision de 99,37%. Un tel changement presque insignifiant fournit une amélioration significative de la précision de la classification. Et, comme nous l'avons vu précédemment, l'extension des données algorithmiques peut être développée davantage. Pour rappel: en 2003,
Simard, Steinkraus et Platt ont amélioré la précision de leur réseau à 99,6%. Leur réseau était similaire au nôtre, ils utilisaient deux couches convolution / pool, suivies d'une couche entièrement connectée avec 100 neurones. Les détails de leur architecture variaient - ils n'avaient pas eu l'occasion de profiter de ReLU, par exemple - mais la clé pour améliorer la qualité du travail était l'expansion des données de formation. Ils y sont parvenus en tournant, transférant et déformant des images d'entraînement du MNIST. Ils ont également développé le processus de «distorsion élastique», émulant les vibrations aléatoires des muscles du bras lors de l'écriture. En combinant tous ces processus, ils ont considérablement augmenté le volume effectif de leur base de données de formation et, de ce fait, ont atteint une précision de 99,6%.
Défi
- L'idée des couches convolutives est de fonctionner quel que soit l'emplacement dans l'image. Mais il peut alors sembler étrange que notre réseau soit mieux formé lorsque nous décalons simplement les images d'entrée. Pouvez-vous expliquer pourquoi cela est en fait tout à fait raisonnable?
Ajout d'une couche supplémentaire entièrement connectée
Est-il possible d'améliorer la situation? Une possibilité est d'utiliser exactement la même procédure, mais en même temps d'augmenter la taille de la couche entièrement connectée. J'ai dirigé le programme avec 300 et 1000 neurones, et j'ai obtenu des résultats respectivement à 99,46% et 99,43%. C'est intéressant, mais pas particulièrement convaincant que le résultat précédent (99,37%).
Qu'en est-il de l'ajout d'une couche supplémentaire entièrement connectée? Essayons d'ajouter une couche supplémentaire entièrement connectée afin d'avoir deux couches cachées entièrement connectées de 100 neurones:
>>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2), activation_fn=ReLU), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2), activation_fn=ReLU), FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU), FullyConnectedLayer(n_in=100, n_out=100, activation_fn=ReLU), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(expanded_training_data, 60, mini_batch_size, 0.03, validation_data, test_data, lmbda=0.1)
Ainsi, j'ai atteint une précision de vérification de 99,43%. Le réseau étendu n'a à nouveau pas amélioré considérablement les performances. Après avoir mené des expériences similaires avec des couches entièrement connectées de 300 et 100 neurones, j'ai obtenu une précision de 99,48% et 99,47%. Inspirant, mais pas comme une vraie victoire.
Que se passe-t-il? Est-il possible que des couches étendues ou supplémentaires entièrement connectées n’aident pas à résoudre le problème MNIST? Ou notre réseau peut-il mieux fonctionner, mais nous le développons dans la mauvaise direction? Nous pourrions peut-être, par exemple, recourir à une régularisation plus stricte pour réduire le recyclage. Une possibilité est la technique de décrochage mentionnée au chapitre 3. Rappelons que l'idée de base de l'exclusion est de supprimer aléatoirement les activations individuelles lors de la formation du réseau. Par conséquent, le modèle devient plus résistant à la perte de preuves individuelles, et il est donc moins probable qu'il s'appuiera sur certaines petites caractéristiques non standard des données de formation. Essayons d'appliquer l'exception à la dernière couche entièrement connectée:
>>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2), activation_fn=ReLU), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2), activation_fn=ReLU), FullyConnectedLayer( n_in=40*4*4, n_out=1000, activation_fn=ReLU, p_dropout=0.5), FullyConnectedLayer( n_in=1000, n_out=1000, activation_fn=ReLU, p_dropout=0.5), SoftmaxLayer(n_in=1000, n_out=10, p_dropout=0.5)], mini_batch_size) >>> net.SGD(expanded_training_data, 40, mini_batch_size, 0.03, validation_data, test_data)
En utilisant cette approche, nous atteignons une précision de 99,60%, ce qui est bien meilleur que les précédents, en particulier notre évaluation de base - un réseau avec 100 neurones cachés, qui donne une précision de 99,37%.
Deux changements méritent d'être notés ici.
Tout d'abord, j'ai réduit le nombre d'époques de formation à 40: l'exception réduit le recyclage et nous apprenons plus vite.
Deuxièmement, les couches cachées entièrement connectées contiennent 1000 neurones, et non 100, comme auparavant. Bien sûr, l'exception, en fait, élimine de nombreux neurones pendant l'entraînement, nous devons donc nous attendre à une sorte d'expansion. En fait, j'ai mené des expériences avec 300 et 1000 neurones, et j'ai reçu une confirmation légèrement meilleure dans le cas de 1000 neurones.
Utilisation de Network Ensemble
Un moyen simple d'améliorer l'efficacité consiste à créer plusieurs réseaux de neurones, puis à les faire voter pour une meilleure classification. Supposons, par exemple, que nous ayons formé 5 NS différents à l'aide de la recette ci-dessus, et que chacun d'eux ait atteint une précision proche de 99,6%. Bien que tous les réseaux présentent une précision similaire, ils peuvent présenter des erreurs différentes en raison d'une initialisation aléatoire différente. Il est raisonnable de supposer que si 5 AN votent, leur classement général sera meilleur que celui de n'importe quel réseau séparément.
Cela semble trop beau pour être vrai, mais assembler de tels ensembles est une astuce commune à la fois à l'Assemblée nationale et à d'autres techniques de MO. Et cela donne en fait une amélioration de l'efficacité: nous obtenons une précision de 99,67%. En d'autres termes, notre ensemble de réseaux classe correctement les 10 000 images de vérification, à l'exception de 33.
Les erreurs restantes sont indiquées ci-dessous. L'étiquette dans le coin supérieur droit est la classification correcte selon les données du MNIST, et dans le coin inférieur droit est l'étiquette reçue par l'ensemble du réseau:
Il vaut la peine de s'attarder sur les images. Les deux premiers chiffres, 6 et 5 sont les vraies erreurs de notre ensemble. Cependant, ils peuvent être compris, une telle erreur pourrait être commise par l'homme. Ce 6 est vraiment très similaire à 0, et 5 est très similaire à 3. La troisième image, soi-disant 8, ressemble vraiment plus à 9. Je suis du côté de l'ensemble des réseaux: je pense qu'il a fait le travail mieux que la personne qui a écrit cette figure. En revanche, la quatrième image, 6, est vraiment mal classée par les réseaux.
Et ainsi de suite. Dans la plupart des cas, la solution réseau semble plausible, et dans certains cas, ils ont mieux classé le chiffre que la personne ne l'a écrit. Dans l'ensemble, nos réseaux font preuve d'une efficacité exceptionnelle, surtout si l'on se souvient qu'ils ont correctement classé 9967 images, que nous ne présentons pas ici.
Dans ce contexte, plusieurs erreurs évidentes peuvent être comprises. Même une personne prudente se trompe parfois. Par conséquent, je ne peux espérer un meilleur résultat que d'une personne extrêmement précise et méthodique. Notre réseau approche la performance humaine.Pourquoi avons-nous appliqué l'exception uniquement aux couches entièrement connectées
Si vous regardez attentivement le code ci-dessus, vous verrez que nous avons appliqué l'exception uniquement aux couches réseau entièrement connectées, mais pas aux couches convolutives. En principe, une procédure similaire peut être appliquée aux couches convolutives. Mais cela n'est pas nécessaire: les couches convolutives ont une résistance intégrée importante au recyclage. Cela est dû au fait que les poids totaux font que les filtres convolutionnels apprennent à la fois sur l'ensemble de l'image. Par conséquent, ils sont moins susceptibles de trébucher sur certaines distorsions locales dans les données de formation. Par conséquent, il n'est pas particulièrement nécessaire de leur appliquer d'autres régularisateurs, tels que des exceptions.Aller de l'avant
Vous pouvez améliorer encore plus l'efficacité de la résolution du problème MNIST. Rodrigo Benenson a mis en place une tablette informative montrant les progrès au fil des ans et les liens avec le travail. Beaucoup d'œuvres utilisent GSS de la même manière que nous les avons utilisées. Si vous fouillez dans votre travail, vous trouverez de nombreuses techniques intéressantes, et vous aimerez peut-être en mettre en œuvre. Dans ce cas, il serait sage de commencer leur mise en œuvre avec un réseau simple qui peut être rapidement formé, et cela vous aidera à commencer rapidement à comprendre ce qui se passe.Pour la plupart, je n'essaierai pas de passer en revue les travaux récents. Mais je ne peux pas résister à une exception. Il s'agit d'une œuvre en 2010. J'aime sa simplicité en elle. Le réseau est multicouche et n'utilise que des couches entièrement connectées (sans circonvolutions). Dans leur réseau le plus performant, il existe des couches cachées contenant respectivement 2500, 2000, 1500, 1000 et 500 neurones. Ils ont utilisé des idées similaires pour élargir les données de formation. Mais en plus de cela, ils ont appliqué plusieurs autres astuces, y compris le manque de couches convolutionnelles: c'était le réseau vanille le plus simple, qui, avec une patience appropriée et la disponibilité de capacités informatiques appropriées, aurait pu être enseigné dans les années 1980 (si l'ensemble MNIST existait alors). Ils ont atteint une précision de classification de 99,65%, ce qui coïncide à peu près avec la nôtre. L'essentiel de leur travail est l'utilisation d'un réseau très vaste et profond et l'utilisation de GPU pour accélérer l'apprentissage. Cela leur a permis d'apprendre de nombreuses époques. Ils ont également profité de la longue durée des intervalles de formation,et a progressivement réduit la vitesse d'apprentissage de 10-3 à 10 -6 . Essayer d'obtenir des résultats similaires avec une architecture comme la leur est un exercice intéressant.Pourquoi apprenons-nous?
Dans le chapitre précédent, nous avons vu des obstacles fondamentaux à l'apprentissage d'une NS multicouche profonde. En particulier, nous avons vu que le gradient devient très instable: lors du passage de la couche de sortie aux précédentes, le gradient a tendance à disparaître (le problème du gradient qui disparaît) ou à une croissance explosive (le problème de la croissance du gradient explosif). Étant donné que le gradient est le signal que nous utilisons pour la formation, cela pose des problèmes.Comment avons-nous réussi à les éviter?La réponse est naturellement la suivante: nous n'avons pas pu les éviter. Au lieu de cela, nous avons fait quelques choses qui nous ont permis de continuer à travailler, malgré cela. En particulier: (1) l'utilisation de couches convolutives réduit considérablement le nombre de paramètres qu'elles contiennent, facilitant considérablement le problème d'apprentissage; (2) l'utilisation de techniques de régularisation plus efficaces (couches d'exclusion et de convolution); (3) utiliser ReLU au lieu des neurones sigmoïdes pour accélérer l'apprentissage - empiriquement jusqu'à 3-5 fois; (4) l'utilisation du GPU et la capacité d'apprendre au fil du temps. En particulier, dans des expériences récentes, nous avons étudié 40 époques en utilisant un ensemble de données 5 fois plus grand que les données d'entraînement MNIST standard. Plus tôt dans le livre, nous avons principalement étudié 30 époques en utilisant des données d'entraînement standard. La combinaison des facteurs (3) et (4) donne un tel effet,comme si on étudiait 30 fois plus longtemps qu'avant.Vous dites probablement: "C'est tout?" Est-ce tout ce qu'il faut pour former des réseaux de neurones profonds? Et à cause de quoi alors l'agitation a pris feu? "Bien sûr, nous avons utilisé d'autres idées: des ensembles de données suffisamment volumineux (pour éviter de se recycler); fonction de coût correcte (pour éviter les ralentissements d'apprentissage); bonne initialisation des poids (également pour éviter de ralentir l'apprentissage en raison de la saturation des neurones); extension algorithmique de l'ensemble de données d'apprentissage. Nous avons discuté de ces idées et d'autres dans les chapitres précédents, et nous avons généralement eu l'occasion de les réutiliser avec de petites notes dans ce chapitre.De toutes les indications, il s'agit d'un ensemble d'idées assez simple. Simple, cependant, capable de beaucoup lorsqu'il est utilisé dans un complexe. Il s'est avéré que commencer avec l'apprentissage en profondeur était assez facile!?
Si nous considérons les couches de convolution / mise en commun comme une seule, alors dans notre architecture finale, il y a 4 couches cachées. Un tel réseau mérite-t-il un titre profond? Naturellement, 4 couches cachées sont bien plus que dans les réseaux peu profonds que nous avons étudiés précédemment. La plupart des réseaux avaient une couche cachée, parfois 2. D'autre part, les réseaux avancés modernes ont parfois des dizaines de couches cachées. Parfois, je rencontrais des gens qui pensaient que plus le réseau est profond, mieux c'est, et que si vous n'utilisez pas un nombre suffisamment important de couches cachées, cela signifie que vous ne faites pas vraiment d'apprentissage en profondeur. Je ne le pense pas, en particulier parce qu'une telle approche transforme la définition de l'apprentissage profond en une procédure qui dépend de résultats momentanés. Une véritable percée dans ce domaine a été l'idée de la possibilité d'aller au-delà des réseaux avec une ou deux couches cachées,au milieu des années 2000. Ce fut une véritable percée, ouvrant un champ de recherche avec des modèles plus expressifs. Eh bien, un nombre spécifique de couches n'est pas d'un intérêt fondamental. L'utilisation de réseaux profonds est un outil pour atteindre d'autres objectifs, tels que l'amélioration de la précision de la classification.Problème de procédure
Dans cette section, nous sommes passés en douceur des réseaux peu profonds à une couche cachée aux réseaux de convolution multicouches. Tout semblait si simple! Nous avons fait un changement et obtenu une amélioration. Si vous commencez à expérimenter, je vous garantis que généralement tout ne se passera pas aussi bien. Je vous ai présenté une histoire peignée, en omettant de nombreuses expériences, y compris celles qui ont échoué. J'espère que cette histoire peignée vous aidera à mieux comprendre les idées de base. Mais il risque de donner une impression incomplète. Obtenir un bon réseau qui fonctionne nécessite beaucoup d'essais et d'erreurs, entrecoupés de frustration. En pratique, vous pouvez vous attendre à un grand nombre d'expériences. Pour accélérer le processus, les informations du chapitre 3 concernant la sélection des hyperparamètres de réseau, ainsi que la documentation supplémentaire mentionnée ici, peuvent vous aider.Code pour nos réseaux de convolution
Bon, regardons maintenant le code de notre programme network3.py. Structurellement, il est similaire à network2.py, que nous avons développé au chapitre 3, mais les détails sont différents en raison de l'utilisation de la bibliothèque Theano. Commençons par la classe FullyConnectedLayer, similaire aux couches que nous avons étudiées plus tôt. class FullyConnectedLayer(object): def __init__(self, n_in, n_out, activation_fn=sigmoid, p_dropout=0.0): self.n_in = n_in self.n_out = n_out self.activation_fn = activation_fn self.p_dropout = p_dropout
La plupart de la méthode __init__ parle d'elle-même, mais quelques notes peuvent aider à clarifier le code. Comme d'habitude, nous initialisons au hasard les poids et les décalages en utilisant des valeurs aléatoires normales avec des écarts-types appropriés. Ces lignes semblent un peu incompréhensibles. Cependant, la plupart du code étrange charge des poids et des décalages dans ce que la bibliothèque Theano appelle des variables partagées. Cela garantit que les variables peuvent être traitées sur le GPU, si elles sont disponibles. Nous ne nous pencherons pas sur ce problème - si vous êtes intéressé, lisez la documentation de Theano. Notez également que cette initialisation des poids et décalages concerne la fonction d'activation sigmoïde. Idéalement, pour des fonctions comme la tangente hyperbolique et ReLU, nous initialiserions différemment les pondérations et les décalages. Ce problème est abordé dans les tâches futures.La méthode __init__ se termine par l'instruction self.params = [self.w, self.b]. Il s'agit d'un moyen pratique de rassembler tous les paramètres d'apprentissage associés à une couche. Network.SGD utilise plus tard les attributs params pour déterminer quelles variables de l'instance de classe Network peuvent être entraînées.La méthode set_inpt est utilisée pour passer l'entrée à une couche et calculer la sortie correspondante. J'écris inpt au lieu d'entrée, car l'entrée est une fonction python intégrée, et si vous jouez avec eux, cela peut entraîner un comportement imprévisible du programme et des erreurs de diagnostic difficiles. En fait, nous transmettons l'entrée de deux manières: via self.inpt et self.inpt_dropout. Cela se fait car nous pouvons vouloir utiliser l'exception pendant la formation. Et puis nous devrons supprimer une partie des neurones self.p_dropout. C'est ce que fait la fonction dropout_layer dans l'avant-dernière ligne de la méthode set_inpt. Ainsi, self.inpt_dropout et self.output_dropout sont utilisés pendant la formation, et self.inpt et self.output sont utilisés à toutes autres fins, par exemple pour évaluer la précision des données de validation et de test.Les définitions de classe pour ConvPoolLayer et SoftmaxLayer sont similaires à FullyConnectedLayer. Si similaire que je ne citerai même pas le code. Si vous êtes intéressé, le code complet du programme peut être étudié plus loin dans ce chapitre.Il convient de mentionner quelques détails différents. De toute évidence, dans ConvPoolLayer et SoftmaxLayer, nous calculons les activations de sortie d'une manière qui convient au type de couche. Heureusement, Theano est facile à faire, il a des opérations intégrées pour calculer la convolution, le max-pooling et la fonction softmax.Il est moins évident d'initialiser les pondérations et les décalages dans la couche softmax - nous n'en avons pas discuté. Nous avons mentionné que pour les couches de poids sigmoïdes, il est nécessaire d'initialiser des distributions aléatoires normales correctement paramétrées. Mais cet argument heuristique s'appliquait aux neurones sigmoïdes (et, avec des corrections mineures, aux neurones tang). Cependant, il n'y a aucune raison particulière pour que cet argument s'applique aux couches softmax. Il n'y a donc aucune raison d'appliquer a priori à nouveau cette initialisation. Au lieu de cela, j'initialise tous les poids et décalages à 0. L'option est spontanée, mais fonctionne plutôt bien en pratique.Nous avons donc étudié toutes les classes de couches. Et la classe Réseau? Commençons par explorer la méthode __init__: class Network(object): def __init__(self, layers, mini_batch_size): """ layers, , mini_batch_size """ self.layers = layers self.mini_batch_size = mini_batch_size self.params = [param for layer in self.layers for param in layer.params] self.x = T.matrix("x") self.y = T.ivector("y") init_layer = self.layers[0] init_layer.set_inpt(self.x, self.x, self.mini_batch_size) for j in xrange(1, len(self.layers)): prev_layer, layer = self.layers[j-1], self.layers[j] layer.set_inpt( prev_layer.output, prev_layer.output_dropout, self.mini_batch_size) self.output = self.layers[-1].output self.output_dropout = self.layers[-1].output_dropout
La plupart du code parle de lui-même. La ligne self.params = [param for layer in ...] rassemble tous les paramètres de chaque couche dans une seule liste. Comme suggéré précédemment, la méthode Network.SGD utilise self.params pour déterminer les paramètres à partir desquels le réseau peut apprendre. Les lignes self.x = T.matrix ("x") et self.y = T.ivector ("y") définissent les variables symboliques Theano x et y. Ils représenteront l'entrée et la sortie souhaitée du réseau.Ce n'est pas un tutoriel sur l'utilisation de Theano, donc je n'entrerai pas dans la signification des variables symboliques (voir la documentation , et aussi l'un des tutoriels) En gros, ils désignent des variables mathématiques, pas des variables spécifiques. Avec eux, vous pouvez effectuer de nombreuses opérations ordinaires: ajouter, soustraire, multiplier, appliquer des fonctions, etc. Theano offre de nombreuses possibilités pour manipuler de telles variables symboliques, convolving, max-pulling, etc. Cependant, l'essentiel est la possibilité d'une différenciation symbolique rapide en utilisant une forme très générale de l'algorithme de rétropropagation. Ceci est extrêmement utile pour appliquer une descente de gradient stochastique à un large éventail d'architectures de réseau. En particulier, les lignes de code suivantes définissent la sortie symbolique du réseau. Nous commençons par affecter l'entrée à la première couche: init_layer.set_inpt(self.x, self.x, self.mini_batch_size)
Les données d'entrée sont transmises un mini-paquet à la fois, donc leur taille y est indiquée. Nous passons l'entrée de self.x deux fois: le fait est que nous pouvons utiliser le réseau de deux manières différentes (avec ou sans exception). La boucle for propage la variable symbolique self.x à travers les couches réseau. Cela nous permet de définir les attributs finaux de sortie et output_dropout, qui représentent symboliquement la sortie du réseau.Après avoir traité l'initialisation du réseau, regardons sa formation à travers la méthode SGD. Le code semble long, mais sa structure est assez simple. Les explications suivent le code: def SGD(self, training_data, epochs, mini_batch_size, eta, validation_data, test_data, lmbda=0.0): """ - .""" training_x, training_y = training_data validation_x, validation_y = validation_data test_x, test_y = test_data
Les premières lignes sont claires, elles séparent les ensembles de données en composants x et y et calculent le nombre de mini-paquets utilisés dans chaque ensemble de données. Les lignes suivantes sont plus intéressantes et montrent pourquoi il est si intéressant de travailler avec la bibliothèque Theano. Je vais les citer ici:
Dans ces lignes, nous définissons symboliquement une fonction de coût régularisée basée sur la fonction de vraisemblance logarithmique, calculons les dérivées correspondantes dans la fonction de gradient, ainsi que les mises à jour des paramètres correspondantes. Theano nous permet de faire tout cela en quelques lignes. La seule chose cachée est que le calcul du coût implique l'invocation de la méthode du coût pour la couche de sortie; ce code se trouve ailleurs dans network3.py. Mais c'est court et simple. Avec la définition de tout cela, tout est prêt à définir la fonction train_mb, la fonction symbolique Theano qui utilise les mises à jour pour mettre à jour les paramètres réseau par index de mini-paquets. De même, les fonctions validate_mb_accuracy et test_mb_accuracy calculent la précision du réseau sur tout mini-paquet donné de données de validation ou de vérification. Faire la moyenne de ces fonctions,nous pouvons calculer la précision sur l'ensemble des ensembles de données de validation et de vérification.Le reste de la méthode SGD parle de lui-même - nous passons simplement par les époques successivement, entraînant le réseau encore et encore sur des mini-paquets de données de formation, et calculons l'exactitude de la confirmation et de la vérification.Nous comprenons maintenant les parties les plus importantes de l'année network3.py. Passons brièvement en revue tout le programme. Il n'est pas nécessaire d'étudier tout cela en détail, mais vous aimerez peut-être parcourir les sommets et peut-être vous plonger dans certains passages particulièrement appréciés. Mais, bien sûr, la meilleure façon de comprendre le programme est de le changer, d'ajouter quelque chose de nouveau, de refactoriser les parties qui, à votre avis, peuvent être améliorées. Après le code, je présente plusieurs tâches qui contiennent un certain nombre de suggestions initiales sur ce qui peut être fait ici. Voici le code. """network3.py ~~~~~~~~~~~~~~ Theano . (, , -, softmax) (, , ReLU; ). CPU , network.py network2.py. , , GPU, . Theano, network.py network2.py. , . , API network2.py. , , . , , . Theano (http://deeplearning.net/tutorial/lenet.html ), (https://github.com/mdenil/dropout ) (http://colah.imtqy.com ). Theano 0.6 0.7, . """
Les tâches
- SGD . , . network3.py , .
- Network , .
- SGD , η ( , , , ).
- , . network3.py, . , , . .
- .
- – . , , , ? .
- ReLU , ( -) . . , ReLU ( ). , c>0 c L−1 , L – . , softmax? ReLU? ? , , . , ReLU.
- . , ReLU? , ? : «» . – , - - .