Discrete Math for WMS: Clustering Stock Lots

L'article décrit comment, lors de l'introduction d'un système WMS , nous avons été confrontés à la nécessité de résoudre un problème de clustering non standard et avec quels algorithmes nous l'avons résolu. Nous allons vous expliquer comment nous avons appliqué une approche systématique et scientifique pour résoudre le problème, quelles difficultés nous avons rencontrées et quelles leçons nous avons apprises.

Cette publication commence une série d'articles dans lesquels nous partageons notre expérience réussie dans la mise en œuvre d'algorithmes d'optimisation dans les processus d'entrepôt. L'objectif de la série d'articles est de familiariser le public avec les types de tâches d'optimisation des opérations d'entrepôt qui se posent dans presque tous les entrepôts moyens et grands, ainsi que de raconter notre expérience dans la résolution de ces problèmes et les pièges rencontrés de cette façon. Les articles seront utiles à ceux qui travaillent dans l'industrie de la logistique d'entrepôt, mettent en œuvre des systèmes WMS , ainsi qu'aux programmeurs qui s'intéressent aux applications mathématiques dans l'optimisation des affaires et des processus dans l'entreprise.

Goulot d'étranglement du processus

En 2018, nous avons réalisé un projet visant à introduire un système WMS dans l'entrepôt de la société LD Trading House à Chelyabinsk. Présentation du produit «1C-Logistics: Warehouse Management 3» pour 20 emplois: opérateurs WMS , magasiniers, conducteurs de chariots élévateurs. Entrepôt moyen d'environ 4 000 m2, le nombre de cellules 5000 et le nombre de SKU 4500. L'entrepôt stocke les vannes à boisseau sphérique de leur propre production dans différentes tailles de 1 kg à 400 kg. Les stocks à l'entrepôt sont stockés dans le cadre de lots en raison de la nécessité de sélectionner les marchandises selon FIFO et les spécificités «en ligne» du placement de produit (explication ci-dessous).

Lors de la conception de schémas d'automatisation pour les processus d'entrepôt, nous avons été confrontés au problème existant de stockage non optimal des stocks. L'empilage et le stockage des grues ont, comme nous l'avons déjà dit, des spécificités de «rang». Autrement dit, les produits dans la cellule sont empilés en rangées les uns sur les autres, et la capacité de mettre un morceau sur un morceau est souvent absente (ils tombent simplement et le poids n'est pas petit). Pour cette raison, il s'avère qu'une seule nomenclature d'un lot peut être dans une unité de stockage en une seule pièce;

Les produits arrivent quotidiennement à l'entrepôt et chaque arrivée est un lot distinct. Au total, à la suite d'un mois de fonctionnement en entrepôt, 30 lots distincts sont créés, malgré le fait que chacun doit être stocké dans une cellule séparée. Les marchandises sont souvent sélectionnées non pas en palettes entières, mais en pièces, et par conséquent, dans la zone de sélection des pièces, dans de nombreuses cellules, l'image suivante est observée: dans une cellule avec un volume de plus de 1 m3, il y a plusieurs pièces de grues qui occupent moins de 5 à 10% du volume de la cellule (voir Fig.1 )

Fig 1. Photo de plusieurs articles dans une cellule

Face à une utilisation sous-optimale de la capacité de stockage. Pour imaginer l’ampleur de la catastrophe, je peux citer les chiffres: en moyenne, il y a entre 100 et 300 cellules de ces cellules avec un reste maigre à différentes périodes du fonctionnement de l’entrepôt. Étant donné que l'entrepôt est relativement petit, pendant les saisons de chargement de l'entrepôt, ce facteur devient un «col étroit» et inhibe considérablement les processus d'entrepôt.

Idée pour résoudre un problème

L'idée est venue: rassembler les lots de résidus avec les dates les plus proches dans un seul lot et placer ces balances avec un lot unifié de manière compacte dans une cellule, ou dans plusieurs s'il n'y a pas assez d'espace dans une pour accueillir le nombre total de balances.


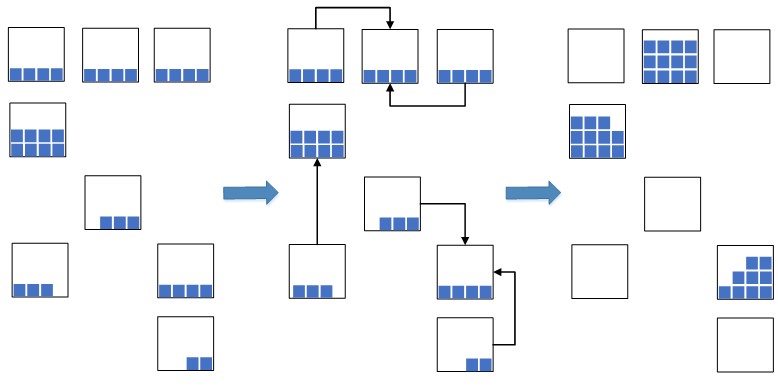Fig.2. Schéma de compression cellulaire

Cela vous permet de réduire considérablement l'espace d'entrepôt occupé, qui sera utilisé pour les marchandises nouvellement placées. Dans une situation de surcharge des capacités d'entrepôt, une telle mesure est extrêmement nécessaire; sinon, il n'y aura tout simplement pas assez d'espace libre pour le placement de nouvelles marchandises, ce qui entraînera un arrêt dans les processus de stockage et de réapprovisionnement de l'entrepôt. Auparavant, avant la mise en œuvre du système WMS , une telle opération était effectuée manuellement, ce qui n'était pas efficace, car le processus de recherche de résidus appropriés dans les cellules était assez long. Maintenant, avec l'introduction des systèmes WMS, ils ont décidé d'automatiser le processus, de l'accélérer et de le rendre intelligent.

Le processus de résolution de ce problème est divisé en 2 étapes:

• au premier stade, nous trouvons des groupes de partis proches pour la compression;
• au deuxième stade, pour chaque groupe de lots, nous calculons le placement le plus compact des résidus de produit dans les cellules.

Dans l'article actuel, nous allons nous concentrer sur la première étape de l'algorithme et laisser la couverture de la deuxième étape pour le prochain article.

Recherche d'un modèle mathématique d'un problème

Avant de nous asseoir pour écrire du code et inventer notre vélo, nous avons décidé d'aborder ce problème scientifiquement, à savoir: le formuler mathématiquement, le réduire au problème d'optimisation discret bien connu et utiliser des algorithmes efficaces efficaces pour le résoudre, ou prendre ces algorithmes existants comme base et les modifier sous les spécificités de la tâche pratique à résoudre.

Puisqu'il résulte clairement de l'énoncé commercial du problème que nous traitons avec les ensembles, nous formulons un tel problème en termes de théorie des ensembles.

Soit $$$P$ - l'ensemble de tous les lots des restes de certaines marchandises en stock. Soit $$$C$ - la constante donnée de jours. Soit $$$K$ - un sous-ensemble de lots où la différence de date pour toutes les paires de lots du sous-ensemble ne dépasse pas la constante $$$C$ . Trouver le nombre minimum de sous-ensembles disjoints $$$K$ de telle sorte que tous les sous-ensembles $$$K$ collectivement donnerait beaucoup $$$P$ .

De plus, nous devons trouver non seulement le nombre minimum de sous-ensembles, mais pour que ces sous-ensembles soient aussi grands que possible. Cela est dû au fait qu'après le regroupement des lots, nous «comprimerons» les restes des lots trouvés dans les cellules. Illustrons par un exemple. Supposons qu'il existe de nombreux partis répartis sur l'axe du temps, comme dans la figure 3.
Fig.3. Options de partitionnement multiples

Des deux options pour diviser l'ensemble P avec le même nombre de sous-ensembles, la première partition (a) est la plus avantageuse pour notre tâche. Depuis, plus les parties seront en groupes, plus les combinaisons de compression apparaissent, et donc plus il est probable de trouver la compression la plus compacte. Bien sûr, une telle règle n'est rien de plus qu'une heuristique et notre hypothèse spéculative. Bien que, comme l'a montré une expérience de calcul, si une telle condition de maximisation est prise en compte, la compacité de la compression subséquente des résidus devient en moyenne 5 à 10% plus élevée que la compression qui a été construite sans tenir compte d'une telle condition.

En d'autres termes, en bref, nous devons trouver des groupes ou des grappes de partis similaires où le critère de similitude est déterminé par une constante $$$C$ . Cette tâche nous rappelle le problème de clustering bien connu. Il est important de dire que le problème considéré diffère du problème de clustering en ce que dans notre problème il y a une condition strictement définie pour le critère de similitude des éléments de cluster, déterminé par la constante $$$C$ , et dans le problème de regroupement, il n'y a pas une telle condition. L'énoncé du problème de clustering et des informations sur cette tâche sont disponibles ici.

Nous avons donc réussi à formuler le problème et à trouver le problème classique avec une formulation similaire. Maintenant, vous devez considérer des algorithmes bien connus pour le résoudre, afin de ne pas réinventer la roue, mais de prendre les meilleures pratiques et de les appliquer. Pour résoudre le problème de clustering, nous avons considéré les algorithmes les plus populaires, à savoir: $$$k$ -signifie $$$c$ -moyens, algorithme de sélection des composants connectés, algorithme de spanning tree minimal. Une description et une analyse de ces algorithmes peuvent être trouvées ici.

Pour résoudre notre problème, les algorithmes de clustering $$$k$ -des moyens et $$$c$ -les moyens ne sont pas du tout applicables, car le nombre de clusters n'est jamais connu à l'avance $$$k$ et de tels algorithmes ne prennent pas en compte la restriction de la constante des jours. Ces algorithmes ont été initialement rejetés.
Pour résoudre notre problème, l'algorithme de sélection des composants connectés et l'algorithme de spanning tree minimum sont plus adaptés, mais, comme il s'est avéré, ils ne peuvent pas être appliqués «de front» au problème résolu et obtenir une bonne solution. Pour clarifier cela, nous considérons la logique du fonctionnement de tels algorithmes appliquée à notre problème.

Considérez le graphique $$$G$ dans lequel les sommets sont beaucoup de fêtes $$$P$ et l'arête entre les sommets $$$p_1$ et $$$p_2$ a un poids égal à la différence de jours entre les lots $$$p_1$ et $$$p_2$ . Dans l'algorithme de sélection des composants connectés, un paramètre d'entrée est spécifié $$$R$ où $$$R \ leq C$ et dans le graphique $$$G$ tous les bords pour lesquels le poids est supprimé sont supprimés $$$R$ . Seules les paires d'objets les plus proches restent connectées. La signification de l'algorithme est de sélectionner une telle valeur $$$R$ , dans lequel le graphique "se désagrège" en plusieurs composants connectés, où les parties appartenant à ces composants satisfont notre critère de similitude, déterminé par la constante $$$C$ . Les composants résultants sont des clusters.

L'algorithme d'arbre couvrant minimal repose d'abord sur un graphique $$$G$ arbre couvrant minimal, puis supprime séquentiellement les bords avec le plus grand poids jusqu'à ce que le graphique "se désagrège" en plusieurs composants connectés, où les lots appartenant à ces composants satisferont également notre critère de similitude. Les composants résultants seront des clusters.

Lors de l'utilisation de ces algorithmes pour résoudre le problème considéré, une situation peut se produire comme dans la figure 4.


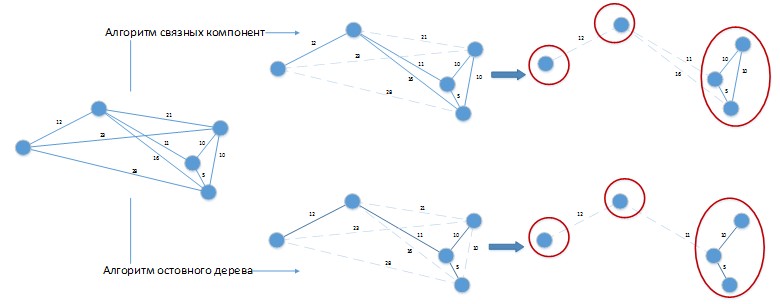Figure 4. Application d'algorithmes de clustering au problème en cours de résolution.

Supposons que nous avons une différence constante des jours des parties est de 20 jours. Compter $$$G$ a été représenté sous une forme spatiale pour la commodité de la perception visuelle. Les deux algorithmes ont donné une solution avec 3 clusters, qui peuvent être facilement améliorés en combinant des lots placés dans des clusters séparés entre eux! De toute évidence, de tels algorithmes doivent être développés davantage en fonction des spécificités du problème à résoudre et leur application pure à la solution de notre problème donnera de mauvais résultats.


Donc, avant de commencer à écrire le code des algorithmes de graphes modifiés pour notre tâche et d'inventer notre propre vélo (dans les silhouettes desquelles les contours des roues carrées étaient déjà devinés), nous avons de nouveau décidé d'aborder ce problème scientifiquement, à savoir: essayer de le réduire à un autre problème discret optimisation, dans l'espoir que les algorithmes existants pour sa solution puissent être appliqués sans modifications.

La prochaine recherche d'un problème classique similaire a réussi! Il a été possible de trouver un problème d'optimisation discret, dont l'énoncé coïncide presque avec 1 sur 1 avec l'énoncé de notre problème. Ce problème s'est avéré être le problème de la couverture de l'ensemble . Nous présentons l'énoncé du problème tel qu'il est appliqué à nos spécificités.

Il y a un ensemble fini $$$P$ et famille $$$S$ de tous ses sous-ensembles de parties disjoints, de sorte que la différence de date pour toutes les paires de parties de chaque sous-ensemble $$$I$ de la famille $$$S$ ne dépasse pas les constantes $$$C$ . Le revêtement est appelé une famille $$$U$ moindre puissance dont les éléments appartiennent $$$S$ de telle sorte que l'union des ensembles $$$I$ de la famille $$$U$ devrait donner beaucoup de toutes les parties $$$P$ .

Une analyse détaillée de ce problème peut être trouvée ici et ici. D'autres options pour l'application pratique du problème de couverture et ses modifications peuvent être trouvées ici.

La seule légère différence entre le problème considéré et le problème classique de la couverture d'un ensemble est la nécessité de maximiser le nombre d'éléments dans les sous-ensembles. Bien sûr, on pourrait rechercher des articles dans lesquels un tel cas spécial a été examiné et, très probablement, on les trouverait. Mais, à partir de la prochaine recherche d'articles, nous avons été sauvés par le fait que l'algorithme bien connu "gourmand" pour résoudre le problème classique de couvrir un ensemble construit une partition en prenant simplement en compte la maximisation du nombre d'éléments dans les sous-ensembles. Nous avons donc pris un peu d'avance et maintenant tout est en ordre.

L'algorithme pour résoudre le problème

Nous avons décidé du modèle mathématique du problème à résoudre. Nous commençons maintenant à considérer l'algorithme pour sa solution. Sous-ensembles $$$I$ de la famille $$$S$ peut être facilement trouvée, par exemple, par une telle procédure.

1. Étape 0. Organisez les lots de l'ensemble $$$P$ dans l'ordre croissant de leurs dates. Nous pensons que toutes les parties ne sont pas marquées comme vues.
2. Étape 1. Trouvez la partie avec la plus petite date parmi les parties non encore vues.
3. Étape 2. Pour la partie trouvée, se déplaçant vers la droite, nous incluons dans le sous-ensemble $$$I$ toutes les parties dont les dates diffèrent de l'actuelle d'au plus $$$C$ jours. Tous les lots inclus dans l'ensemble $$$I$ marquer comme vu.
4. Étape 3. Si, lors du déplacement vers la droite, le lot suivant ne peut pas être inclus dans $$$I$ , puis passez à l'étape 1.

Le problème de couvrir un ensemble est $$$NP$ - difficile, ce qui signifie que pour sa solution il n'y a pas d'algorithme rapide (avec un temps de fonctionnement égal à un polynôme des données d'entrée) et précis. Par conséquent, pour résoudre le problème de la couverture de l'ensemble, un algorithme rapide et gourmand a été choisi, ce qui bien sûr n'est pas exact, mais présente les avantages suivants:

• Pour les problèmes de petite dimension (et ce n'est que notre cas), il calcule des solutions suffisamment proches de l'optimum. À mesure que la taille du problème augmente, la qualité de la solution se détériore, mais encore assez lentement;
• Très facile à mettre en œuvre;
• Rapide, puisque l'estimation de sa durée de fonctionnement est $$$O (mn)$ .

L'algorithme gourmand sélectionne des ensembles guidés par la règle suivante: à chaque étape, un ensemble est sélectionné qui couvre le nombre maximum d'éléments non encore couverts. Une description détaillée de l'algorithme et de son pseudo-code peut être trouvée ici. L'implémentation de l'algorithme en langage 1C dans le spoiler est plus faible (pourquoi ils ont commencé à l'implémenter en langage "jaune" dans le chapitre suivant).


Bien sûr, l'optimalité d'un tel algorithme est hors de question - l'heuristique, pour ne rien dire. Vous pouvez trouver de tels exemples sur lesquels un tel algorithme serait erroné. De telles erreurs surviennent lorsque, à une certaine itération, nous trouvons plusieurs ensembles avec le même nombre d'éléments et sélectionnons le premier qui apparaît, car la stratégie est gourmande: j'ai pris la première chose qui a attiré mon attention et le «gourmand» a été satisfait.

Il se pourrait bien qu'un tel choix conduise à des résultats sous-optimaux lors des itérations suivantes. Mais la précision d'un algorithme aussi simple est toujours assez bonne dans la plupart des cas. Si vous voulez obtenir la solution au problème avec plus de précision, vous devez utiliser des algorithmes plus complexes, par exemple, comme au travail : un algorithme probabiliste gourmand, un algorithme de colonie de fourmis, etc. Les résultats de la comparaison de ces algorithmes sur les données aléatoires générées peuvent être trouvés dans le travail.

Implémentation et implémentation de l'algorithme

Un tel algorithme a été implémenté en langage 1C et a été inclus dans un traitement externe appelé "Compression des résidus", qui était connecté au système WMS . Nous n'avons pas implémenté l'algorithme en C ++ et l'avons utilisé à partir d'un composant natif externe, ce qui serait plus correct, car la vitesse du code C ++ est plusieurs fois et dans certains exemples, même dix fois plus rapide que la vitesse d'un code similaire en 1C . Dans 1C, l' algorithme a été implémenté pour gagner du temps de développement et faciliter le débogage sur la base de travail du client. Le résultat de l'algorithme est illustré à la figure 6.


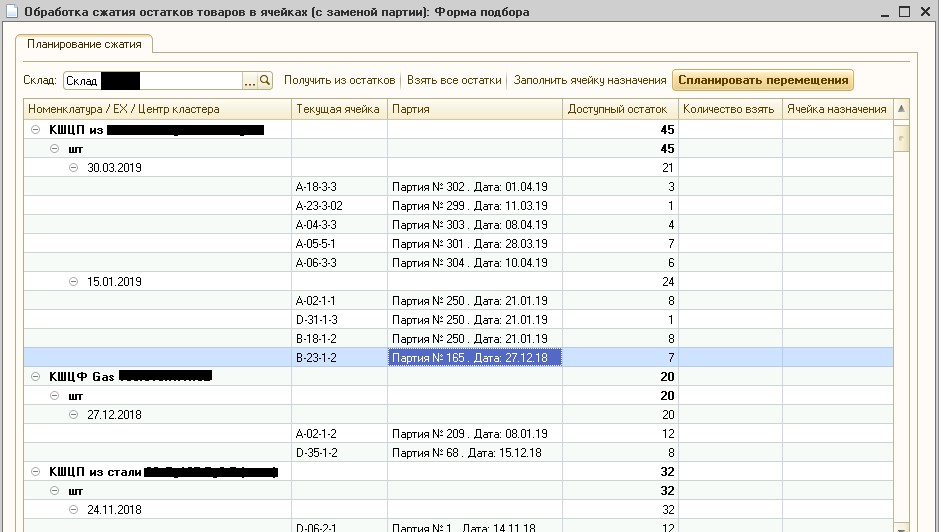Fig.6. Traitement de compression des résidus

La figure 6 montre que, dans l'entrepôt indiqué, les stocks actuels de marchandises dans les cellules de stockage ont été divisés en grappes, à l'intérieur desquelles les dates d'envois ne diffèrent pas de plus de 30 jours. Étant donné que le client fabrique et stocke des robinets à tournant sphérique en métal avec une durée de vie de plusieurs années, cette différence de date peut être négligée. A noter qu'actuellement un tel traitement est systématiquement utilisé en production, et les opérateurs WMS confirment la bonne qualité du clustering batch.

Conclusions et suite

L'expérience principale que nous avons acquise en résolvant un problème aussi pratique est de confirmer l'efficacité de l'utilisation du paradigme: Mat. énoncé de tâche $$$\ rightarrow$ célèbre tapis. le modèle $$$\ rightarrow$ algorithme célèbre $$$\ rightarrow$ algorithme tenant compte des spécificités de la tâche. Il y a déjà plus de 300 ans d'optimisation discrète et pendant ce temps, les gens ont réussi à considérer beaucoup de problèmes et à acquérir beaucoup d'expérience pour les résoudre. Tout d'abord, il est plus judicieux de se tourner vers cette expérience, et alors seulement de commencer à réinventer votre vélo.

Il est également important de dire que la solution au problème de regroupement pourrait être envisagée non pas indépendamment de la solution au problème de la compression du reste des parties, mais pour résoudre ces problèmes ensemble. Autrement dit, pour sélectionner une telle partition de parties en clusters qui donnerait la meilleure compression. Mais la solution à ces problèmes a été décidée pour les raisons suivantes:

• Budget limité pour le développement d'algorithmes. Le développement d'un tel algorithme général, et donc plus complexe, prendrait plus de temps.
• La complexité du débogage et des tests. L'algorithme général serait plus difficile à tester et à déboguer au stade de l'acceptation, et les bogues qu'il contient seraient plus difficiles et plus longs à déboguer en temps réel. Par exemple, une erreur s'est produite et on ne sait pas où creuser: les feutres de toiture vers le clustering, les feutres de toiture vers la compression?
• Transparence et gérabilité. La séparation des deux tâches rend le processus de compression plus transparent, et donc plus facile à gérer pour les utilisateurs finaux - les opérateurs WMS. Ils peuvent supprimer certaines cellules de la compression ou modifier la quantité compressible pour une raison quelconque.

Dans le prochain article, nous continuerons la discussion sur les algorithmes d'optimisation et considérerons les plus intéressants et beaucoup plus complexes: l'algorithme optimal pour la «compression» des résidus dans les cellules, qui utilise comme entrée les données reçues de l'algorithme de clustering par lots.

Préparé un article
Roman Shangin, programmeur, département des projets,
Première entreprise BIT, Chelyabinsk