Alors, imaginez. 5 chats sont enfermés dans la chambre, et pour aller réveiller le propriétaire, ils doivent tous s'entendre à ce sujet, car ils ne peuvent ouvrir la porte qu'en s'appuyant sur cinq d'entre eux. Si l'un des chats est un chat Schrodinger et que les autres chats ne connaissent pas sa solution, la question se pose: "Comment peuvent-ils faire cela?"
Dans cet article, je vais vous parler dans un langage simple de la composante théorique du monde des systèmes distribués et des principes de leur fonctionnement. Et aussi considérer superficiellement l'idée principale sous-jacente à Paxos'a.
Lorsque les développeurs utilisent des infrastructures cloud, diverses bases de données, travaillent en grappes à partir d'un grand nombre de nœuds, ils sont sûrs que les données seront complètes, sécurisées et toujours accessibles. Mais où sont les garanties?
En fait, les garanties que nous avons sont les garanties du fournisseur. Ils sont décrits dans la documentation de la manière suivante: «Ce service est assez fiable, il a un SLA prédéfini, ne vous inquiétez pas, tout fonctionnera de manière distribuée, comme vous vous en doutez.»
Nous avons tendance à croire au meilleur, car les oncles intelligents des grandes entreprises nous ont assuré que tout irait bien. Nous ne nous demandons pas: pourquoi, en fait, cela peut-il même fonctionner? Existe-t-il une justification officielle au bon fonctionnement de ces systèmes?
Je suis récemment allé
à l'école d'informatique distribuée et j'ai été très inspiré par ce sujet. Les conférences à l'école ressemblaient plus à des cours d'analyse mathématique qu'à quelque chose de lié aux systèmes informatiques. Mais c'est précisément ainsi que les algorithmes les plus importants que nous utilisons quotidiennement sans le savoir ont été prouvés à un moment donné.
La plupart des systèmes distribués modernes utilisent l'algorithme de consensus Paxos et ses diverses modifications. Le plus cool est que la validité et, en principe, la possibilité même de l'existence de cet algorithme peuvent être prouvées simplement avec un stylo et du papier. Cependant, dans la pratique, l'algorithme est utilisé dans les grands systèmes fonctionnant sur un grand nombre de nœuds dans les nuages.
Légère illustration de ce qui sera discuté plus loin: la tâche de deux générauxJetons un œil à la
tâche de deux généraux de se réchauffer.
Nous avons deux armées - rouge et blanche. Les troupes blanches sont basées dans la ville assiégée. Les troupes rouges dirigées par les généraux A1 et A2 sont situées des deux côtés de la ville. La tâche des rousses est d'attaquer la ville blanche et de gagner. Cependant, l'armée de chaque général roux individuellement est plus petite que les troupes des blancs.
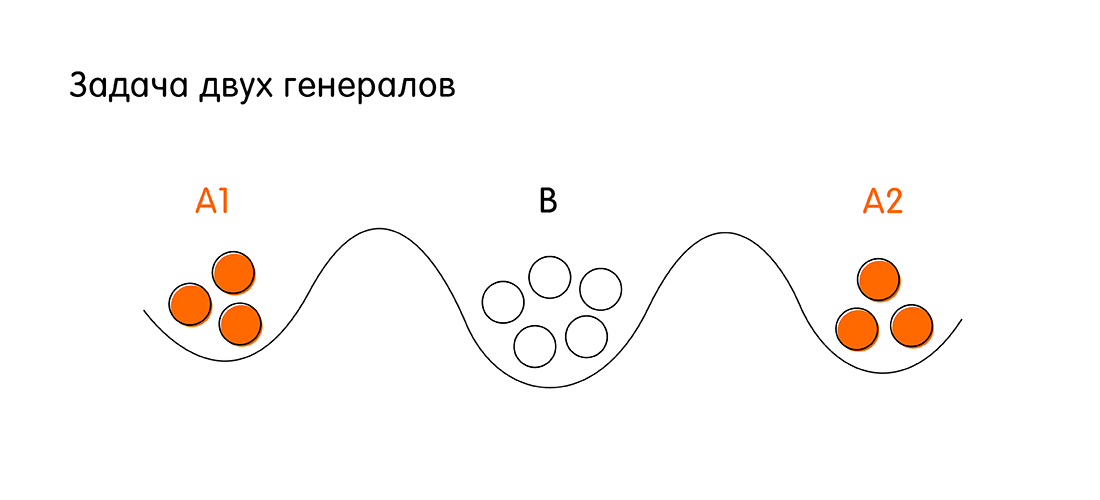
Conditions de victoire pour les roux: les deux généraux doivent attaquer simultanément pour avoir un avantage numérique sur les blancs. Pour cela, les généraux A1 et A2 doivent s'entendre. Si tout le monde attaque individuellement, les roux perdront.
Pour convenir, les généraux A1 et A2 peuvent s’envoyer des messagers à travers le territoire de la ville blanche. Un messager peut réussir à atteindre un général allié ou peut être intercepté par un adversaire. Question: existe-t-il une telle séquence de communications entre les généraux rouges (la séquence d'envoi de messagers de A1 à A2 et vice versa de A2 à A1), dans laquelle ils sont garantis de s'entendre sur une attaque à l'heure X. Ici, sous les garanties, il est entendu que les deux généraux auront une confirmation sans équivoque qu'un allié (un autre général) attaque avec précision à l'heure fixée X.
Supposons que A1 envoie un messager à A2 avec le message: "Attaquons aujourd'hui à minuit!" Le général A1 ne peut pas attaquer sans confirmation du général A2. Si le messager a atteint A1, alors le général A2 envoie une confirmation avec le message: "Oui, remplissons les blancs aujourd'hui." Mais maintenant, le général A2 ne sait pas si son messager est arrivé ou non, il n'a aucune garantie si l'attaque sera simultanée. Le général A2 doit à nouveau être confirmé.
Si nous planifions davantage leur communication, il s'avère que: quel que soit le nombre de cycles de messagerie, il n'y a aucun moyen de garantir d'informer les deux généraux que leurs messages ont été reçus (à condition que l'un des messagers puisse être intercepté).
La tâche de deux généraux est une excellente illustration d'un système distribué très simple où il y a deux nœuds avec une communication peu fiable. Nous n'avons donc pas de garantie à 100% qu'ils sont synchronisés. À propos de problèmes similaires uniquement à plus grande échelle plus loin dans l'article.
Nous introduisons le concept de systèmes distribués
Un système distribué est un groupe d'ordinateurs (ci-après appelés nœuds) qui peuvent échanger des messages. Chaque nœud individuel est une entité autonome. Un nœud peut traiter indépendamment des tâches, mais pour interagir avec d'autres nœuds, il doit envoyer et recevoir des messages.
Comment spécifiquement les messages sont mis en œuvre, quels protocoles sont utilisés - cela ne nous intéresse pas dans ce contexte. Il est important que les nœuds d'un système distribué puissent échanger des données entre eux en envoyant des messages.
La définition elle-même ne semble pas très compliquée, mais vous devez considérer qu'un système distribué possède un certain nombre d'attributs qui seront importants pour nous.
Attributs système distribués
- Concurrence - la possibilité d'événements simultanés ou compétitifs dans le système. De plus, nous considérerons que les événements qui se sont produits sur deux nœuds différents sont potentiellement compétitifs tant que nous n'avons pas un ordre clair d'occurrence de ces événements. Et, en règle générale, nous ne l'avons pas.
- L'absence d'horloge mondiale . Nous n'avons pas un ordre clair des événements en raison de l'absence d'une horloge mondiale. Dans le monde ordinaire des gens, nous sommes habitués au fait que nous avons absolument des heures et du temps. Tout change en matière de systèmes distribués. Même les horloges atomiques ultra-précises ont une dérive, et il peut y avoir des situations où nous ne pouvons pas dire lequel des deux événements s'est produit plus tôt. Par conséquent, nous ne pouvons pas non plus compter sur le temps.
- Défaillance indépendante des nœuds du système . Il y a un autre problème: quelque chose n'est peut-être pas aussi simple car nos nœuds ne sont pas éternels. Le disque dur peut échouer, la machine virtuelle dans le cloud redémarrera, le réseau peut clignoter et les messages seront perdus. De plus, des situations sont possibles lorsque les nœuds fonctionnent, mais en même temps contre le système. Cette dernière classe de problèmes a même reçu un nom distinct: le problème des généraux byzantins . L'exemple le plus populaire d'un système distribué avec un tel problème est Blockchain. Mais aujourd'hui, nous ne considérerons pas cette classe particulière de problèmes. Nous nous intéresserons aux situations dans lesquelles un ou plusieurs nœuds peuvent tomber en panne.
- Modèles de communication (modèles de messagerie) entre les nœuds . Nous avons déjà découvert que les nœuds communiquent via la messagerie. Il existe deux modèles de messagerie bien connus: synchrone et asynchrone.
Modèles de communication entre les nœuds dans les systèmes distribués
Modèle synchrone - nous savons avec certitude qu'il existe un delta temporel connu fini pour lequel un message est garanti d'atteindre d'un nœud à un autre. Si ce temps s'est écoulé, mais que le message n'est pas arrivé, nous pouvons dire en toute sécurité que le nœud a échoué. Dans un tel modèle, nous avons un temps d'attente prévisible.
Modèle asynchrone - dans les modèles asynchrones, nous pensons que le temps d'attente est fini, mais il n'y a pas un tel temps delta après lequel il peut être garanti que le nœud est hors service. C'est-à-dire le temps d'attente pour un message du nœud peut être arbitrairement long. Il s'agit d'une définition importante et nous en reparlerons plus loin.
Le concept de consensus dans les systèmes distribués
Avant de définir formellement le concept de consensus, considérons un exemple de la situation lorsque nous en avons besoin, à savoir la
réplication de machine d'état .
Nous avons un journal distribué. Nous souhaitons qu'il soit cohérent et contienne des données identiques sur tous les nœuds d'un système distribué. Lorsqu'un des nœuds découvre une nouvelle valeur qu'il va écrire dans le journal, sa tâche consiste à proposer cette valeur à tous les autres nœuds afin que le journal soit mis à jour sur tous les nœuds et que le système passe à un nouvel état cohérent. Il est important que les nœuds s'accordent entre eux: tous les nœuds conviennent que la nouvelle valeur proposée est correcte, tous les nœuds acceptent cette valeur, et seulement dans ce cas, tout le monde peut écrire une nouvelle valeur dans le journal.
En d'autres termes: aucun des nœuds ne s'est opposé à ce qu'il dispose d'informations plus pertinentes et la valeur proposée est incorrecte. L'accord entre les nœuds et l'accord sur une seule valeur acceptée correcte est un consensus dans un système distribué. Plus loin, nous parlerons d'algorithmes qui permettent à un système distribué d'atteindre un consensus avec garantie.

Plus formellement, nous pouvons définir un algorithme de consensus (ou simplement un algorithme de consensus) comme une fonction qui transfère un système distribué de l'état A à l'état B.De plus, cet état est accepté par tous les nœuds, et tous les nœuds peuvent le confirmer. Il s'avère que cette tâche n'est pas du tout aussi triviale qu'elle semble à première vue.
Propriétés de l'algorithme de consensus
L'algorithme de consensus doit avoir trois propriétés pour que le système continue d'exister et ait une sorte de progrès dans la transition d'un état à l'autre:
- Accord - tous les nœuds qui fonctionnent correctement doivent prendre la même valeur (dans les articles, cette propriété se trouve également comme propriété de sécurité). Tous les nœuds qui fonctionnent maintenant (qui ne sont pas en panne et qui n'ont pas perdu le contact avec les autres) devraient se mettre d'accord et prendre une sorte de signification générale finale.
Il est important de comprendre ici que les nœuds du système distribué que nous envisageons veulent être d'accord. Autrement dit, nous parlons maintenant de systèmes qui pourraient simplement échouer (par exemple, faire échouer un nœud), mais ce système n'a certainement pas de nœuds qui fonctionnent intentionnellement contre d'autres (la tâche des généraux byzantins). En raison de cette propriété, le système reste cohérent. - Intégrité - si tous les nœuds fonctionnant correctement offrent la même valeur de v , alors chaque nœud fonctionnant correctement doit accepter cette valeur de v .
- Terminaison - tous les nœuds fonctionnant correctement prendront éventuellement une certaine valeur (propriété de vivacité), ce qui permet à l'algorithme de progresser dans le système. Chaque nœud individuel qui fonctionne correctement doit tôt ou tard accepter la valeur finale et la confirmer: "Pour moi, cette valeur est vraie, je suis d'accord avec l'ensemble du système."
Exemple d'algorithme de consensus
Jusqu'à présent, les propriétés de l'algorithme peuvent ne pas être entièrement claires. Par conséquent, nous illustrons avec un exemple les étapes que l'algorithme de consensus le plus simple traverse dans un système avec un modèle de messagerie synchrone, dans lequel tous les nœuds fonctionnent comme prévu, les messages ne sont pas perdus et rien ne casse (est-ce vraiment le cas?).
- Tout commence par une proposition de mariage (Proposer). Supposons qu'un client se connecte à un nœud appelé «Node 1» et démarre une transaction, en transmettant une nouvelle valeur au nœud - O. Dorénavant, «Node 1», nous appellerons proposer. En tant que proposant, «Node 1» devrait maintenant informer l'ensemble du système qu'il a de nouvelles données, et il enverra des messages à tous les autres nœuds: «Regardez! J'ai obtenu la valeur «O» et je veux l'écrire! Veuillez confirmer que vous inscrirez également «O» dans votre journal. »
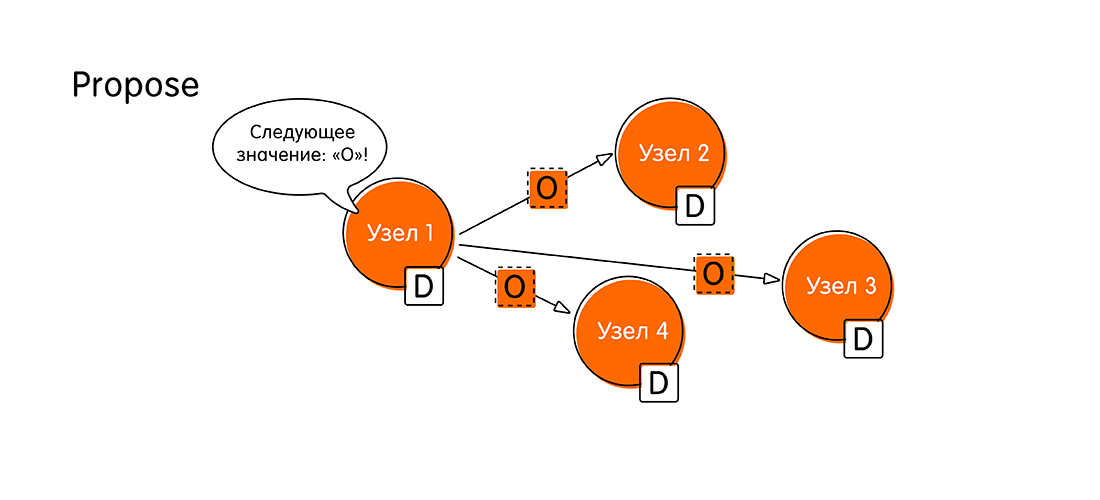
- L'étape suivante consiste à voter pour la valeur proposée (vote). À quoi ça sert? Il peut arriver que d'autres nœuds reçoivent des informations plus récentes et disposent de données sur la même transaction.
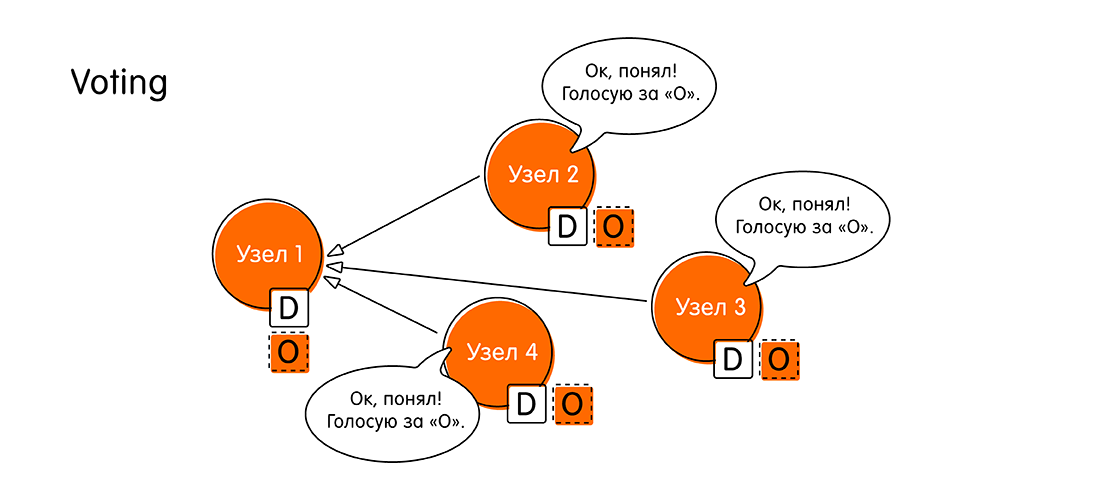
Lorsque le nœud «Node 1» envoie son propre message, les nœuds restants vérifient les données de cet événement dans leurs journaux. S'il n'y a pas de contradictions, les nœuds annoncent: «Oui, je n'ai pas d'autres données sur cet événement. La valeur «O» est la dernière information que nous méritons. »
Dans tous les autres cas, les nœuds peuvent répondre «Nœud 1»: «Écoutez! J'ai des données plus récentes sur cette transaction. Pas "Oh", mais quelque chose de mieux. "
Au stade du vote, les nœuds se prononcent: soit chacun prend la même valeur, soit l'un vote contre, indiquant qu'il dispose de données plus récentes. - Si le tour de scrutin a réussi et que tout le monde y était favorable, le système passe à une nouvelle étape - l'acceptation de la valeur (Accept). «Node 1» recueille toutes les réponses des autres nœuds et signale: «Tout le monde était d'accord avec la valeur« O »! Maintenant, je déclare officiellement que «O» est notre nouveau sens, le même pour tous! Écrivez-vous dans un livret, n'oubliez pas. Écrivez à votre journal! ”
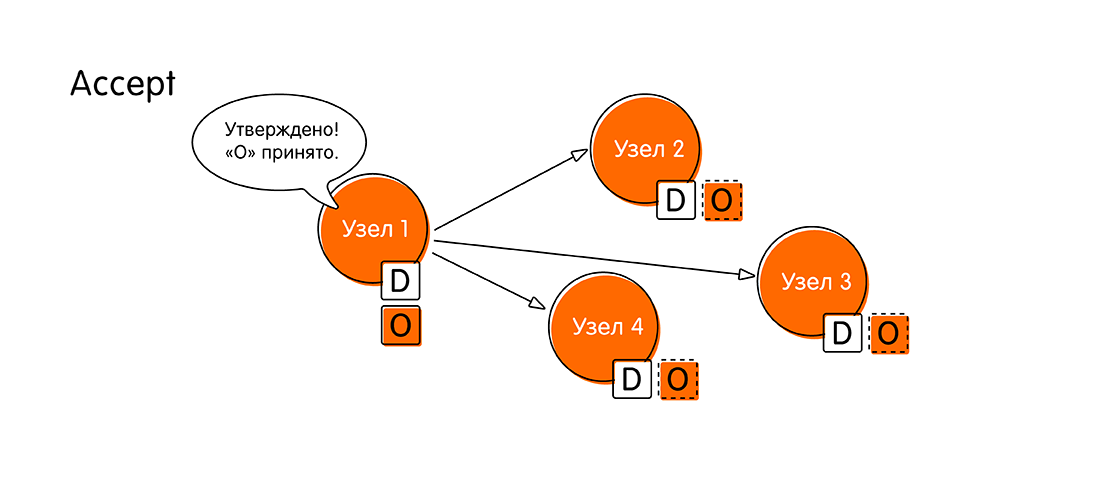
- Les nœuds restants envoient une confirmation (acceptée) qu'ils ont écrit la valeur "O", ils n'ont pas réussi à faire quelque chose de nouveau pendant ce temps (une sorte de validation en deux phases). Après cet événement capital, nous pensons que la transaction distribuée est terminée.
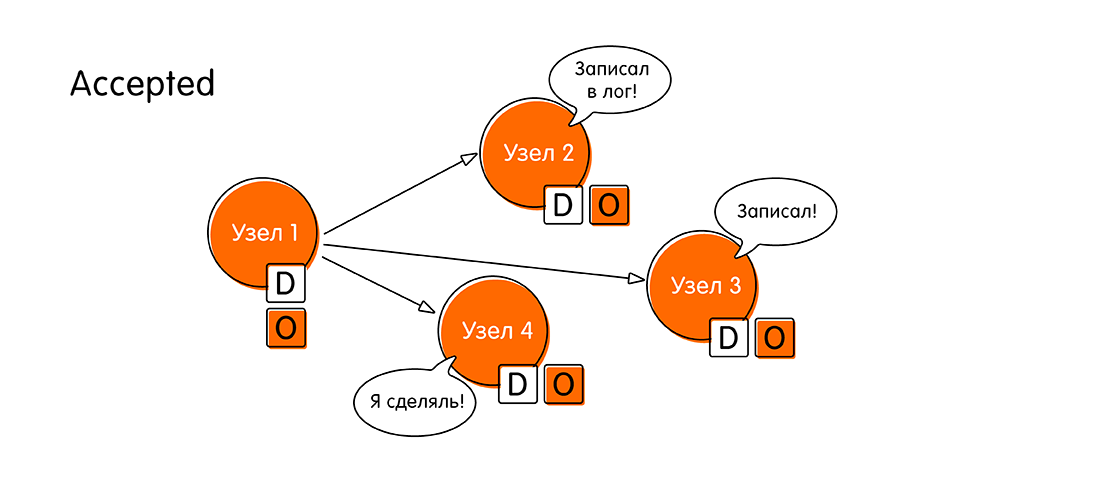
Ainsi, l'algorithme de consensus dans le cas simple comprend quatre étapes: proposer, voter, accepter, confirmer l'acceptation.
Si à un moment donné, nous ne parvenions pas à un accord, alors l'algorithme est redémarré, en tenant compte des informations fournies par les nœuds qui ont refusé de confirmer la valeur proposée.
Algorithme de consensus dans un système asynchrone
Avant cela, tout se passait bien, car il s'agissait d'un modèle de messagerie synchrone. Mais nous savons que dans le monde moderne, nous sommes habitués à tout faire de manière asynchrone. Comment fonctionne un algorithme similaire dans un système avec un modèle de messagerie asynchrone, où nous pensons que le temps d'attente d'une réponse d'un nœud peut être arbitrairement long (à propos, la défaillance d'un nœud peut également être considérée comme un exemple lorsqu'un nœud peut répondre pendant une durée arbitrairement longue) )
Maintenant que nous savons comment fonctionne l'algorithme de consensus, la question est pour les lecteurs curieux qui ont atteint ce point: combien de nœuds dans un système de N nœuds avec un modèle de message asynchrone peuvent échouer afin que le système puisse toujours atteindre un consensus?
La bonne réponse et la justification derrière le spoiler.La bonne réponse est
0 . Si au moins un nœud du système asynchrone tombe en panne, le système ne parvient pas à un consensus. Cette affirmation est prouvée dans le théorème FLP connu dans certains milieux (1985, Fischer, Lynch, Paterson, lien vers l'original à la fin de l'article): «L'incapacité à atteindre un consensus distribué lorsqu'au moins un nœud tombe en panne».
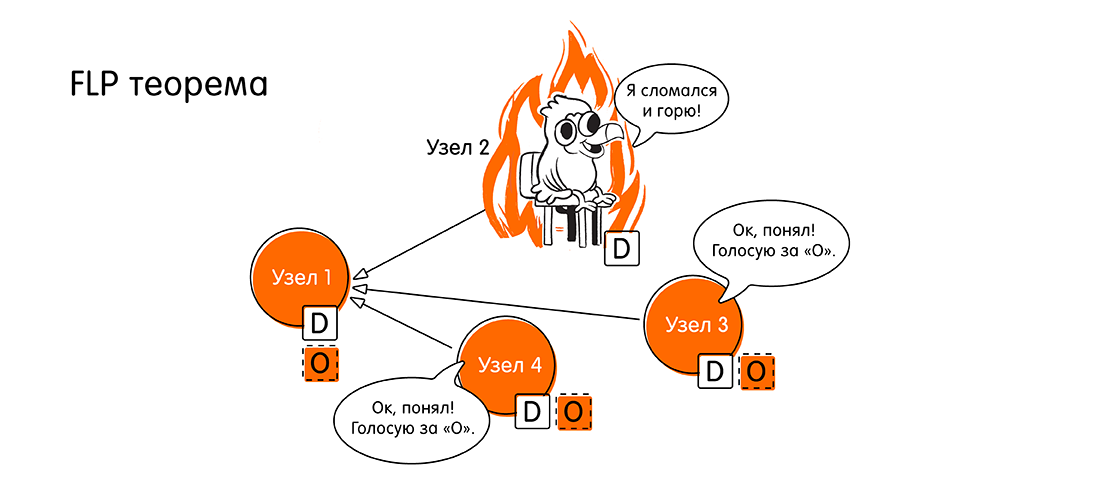
Les gars, alors nous avons un problème, nous sommes habitués au fait que tout est asynchrone avec nous. Et voilà. Comment vivre plus loin?
Nous parlons maintenant de théorie, de mathématiques. Qu'est-ce que cela signifie "un consensus ne peut pas être atteint", traduisant d'un langage mathématique dans le nôtre - l'ingénierie? Cela signifie que «ne peut pas toujours être atteint», c'est-à-dire il y a un cas où le consensus n'est pas réalisable. Et quel est ce cas?
Il s'agit simplement d'une violation de la propriété d'animation décrite ci-dessus. Nous n'avons pas d'accord général, et le système ne peut pas progresser (ne peut pas se terminer dans un temps fini) dans le cas où nous n'avons pas de réponse de tous les nœuds. Parce que dans un système asynchrone, nous n'avons pas de temps de réponse prévisible et nous ne pouvons pas savoir si le nœud est en panne ou prend juste beaucoup de temps pour répondre.
Mais en pratique, nous pouvons trouver une solution. Laissez notre algorithme fonctionner longtemps en cas d'échecs (il peut potentiellement fonctionner à l'infini). Mais dans la plupart des situations, lorsque la plupart des nœuds fonctionnent correctement, nous aurons des progrès dans le système.
Dans la pratique, nous avons affaire à des modèles de communication partiellement synchrones. Le synchronisme partiel est compris comme suit: dans le cas général, nous avons un modèle asynchrone, mais formellement, nous introduisons un certain concept de «temps de stabilisation globale» d'un certain moment dans le temps.
Ce moment peut ne pas arriver aussi longtemps que vous le souhaitez, mais un jour il doit arriver. Une alarme virtuelle va sonner, et à partir de maintenant, nous pouvons prédire le delta de temps pendant lequel les messages atteindront. A partir de ce moment, le système passe d'asynchrone à synchrone. Dans la pratique, nous traitons précisément de tels systèmes.
L'algorithme Paxos résout les problèmes de consensus
Paxos est une famille d'algorithmes qui résolvent le problème du consensus pour les systèmes partiellement synchrones, à condition que certains nœuds puissent tomber en panne. L'auteur de Paxos est
Leslie Lamport . Il a proposé une preuve formelle de l'existence et de l'exactitude de l'algorithme en 1989.
Mais la preuve n'était nullement anodine. La première publication n'a été publiée qu'en 1998 (33 pages) avec une description de l'algorithme. Il s'est avéré qu'il était extrêmement difficile à comprendre et, en 2001, une explication a été publiée pour l'article, qui comptait 14 pages. Les volumes de publications sont donnés afin de montrer qu'en fait, le problème du consensus n'est pas du tout simple, et de tels algorithmes sont soumis à l'énorme travail des personnes les plus intelligentes.
Il est intéressant de noter que Leslie Lamport lui-même dans sa conférence a noté que dans le deuxième article-explication, il y a une déclaration, une ligne (n'a pas précisé laquelle), qui peut être interprétée différemment. - Paxos .
Paxos' , . .
Paxos
Paxos . ( ):
- Proposers ( : ) . , - . . Paxos .
- Acceptors (Voters) . , . , : ( ) .
- Learners . , , . , .
.
,
N .
F . F , ,
2F + 1 acceptor'.
, , «», .
F + 1 «» , , . , . , .
Paxos
Paxos , :
- Phase 1a: Prepare . (proposer) : « . . – n. ». , . . , , . , . , , .
- Phase 1b: Promise . -acceptor' , :
- n , , acceptor. acceptor , , n. acceptor - (.. - ), , .
- , acceptor , .
- Phase 2a: Accept . ( ) , , :
- acceptor' , . c . x, : «Accept (n, x)», – Propose, – , .. , , .
- acceptor' , , , , . y. : «Accept (n, y)», .
- Phase 2b: Accepted . , -acceptor', «Accept(...)», ( , ) , - () n' > n , .
, , . ! , , .
Paxos. , , , .
, Paxos — , , ,
Raft ,
.
«»:
« »:
- Impossibility of Distributed Consensus with One Faulty Process (FLP impossibility) , Fischer, Lynch and Paterson, research paper, 1985
- The Part-Time Parliament , Leslie Lamport, research paper, 1998
- Paxos made simple , Leslie Lamport, research paper, 2001