Mathématiques discrètes pour WMS: algorithme de compression des marchandises dans les cellules (partie 1)

Dans l'article, nous vous expliquerons comment résoudre le problème du manque de cellules libres dans l'entrepôt et le développement d'un algorithme d'optimisation discret pour résoudre ce problème. Nous parlerons de la façon dont nous avons «construit» le modèle mathématique du problème d'optimisation et des difficultés que nous avons rencontrées de manière inattendue lors du traitement des données d'entrée pour l'algorithme.

Si vous êtes intéressé par les applications mathématiques en entreprise et que vous n'avez pas peur des transformations rigoureusement identiques des formules au niveau 5e année, alors bienvenue au chat!

L'article sera utile à ceux qui mettent en œuvre des systèmes WMS , travaillent dans l'entrepôt ou l'industrie de la logistique de production, ainsi qu'aux programmeurs qui s'intéressent aux applications mathématiques dans les affaires et à l'optimisation des processus dans l'entreprise.

Partie introductive

Cette publication poursuit la série d'articles dans lesquels nous partageons notre expérience réussie dans la mise en œuvre d'algorithmes d'optimisation dans les processus d'entrepôt.

L' article précédent décrivait les spécificités de l'entrepôt dans lequel nous avons introduit le système WMS et expliquait également pourquoi nous devions résoudre le problème du regroupement des stocks de marchandises en consignation lors de la mise en œuvre du système WMS , et comment nous l'avons fait.

Lorsque nous avons fini d'écrire un article sur les algorithmes d'optimisation, il s'est avéré être très volumineux, nous avons donc décidé de diviser le matériel accumulé en 2 parties:

• Dans la première partie (cet article), nous parlerons de la façon dont nous avons «construit» le modèle mathématique du problème, et des grandes difficultés que nous avons rencontrées soudainement lors du traitement et de la conversion des données d'entrée pour l'algorithme.
• Dans la deuxième partie, nous examinerons en détail la mise en œuvre de l'algorithme en C ++ , réaliserons une expérience informatique et résumerons l'expérience que nous avons acquise lors de la mise en œuvre de ces «technologies intelligentes» dans les processus commerciaux du client.

Comment lire un article. Si vous lisez l'article précédent, vous pouvez immédiatement vous rendre dans le chapitre "Présentation des solutions existantes", sinon, la description du problème à résoudre dans le spoiler ci-dessous.

Aperçu des solutions existantes

Avant de passer à la description des algorithmes développés par nous, il est utile de procéder à un bref examen des systèmes WMS existants sur le marché qui mettent en œuvre une fonctionnalité de compression optimale similaire.

Tout d'abord, il faut noter le produit «1C: Enterprise 8. WMS Logistics. Warehouse Management 4 ”, qui est détenu et répliqué par 1C et appartient à la quatrième génération de systèmes WMS développés par AXELOT. Dans ce système, la fonctionnalité de compression est déclarée, qui est conçue pour combiner des résidus de produits disparates dans une cellule commune. Il convient de mentionner que la fonctionnalité de compression dans un tel système comprend également d'autres fonctionnalités, par exemple, la correction du placement des marchandises dans les cellules en fonction de leurs classes ABC, mais nous ne nous attarderons pas sur elles.

Si vous analysez le code du système "1C: Enterprise 8. WMS Logistics. Warehouse Management 4 ”(qui est ouvert dans cette partie de la fonctionnalité), nous pouvons conclure ce qui suit. L'algorithme de compression résiduelle implémente une logique linéaire plutôt primitive et on ne peut parler d'aucune compression «optimale». Naturellement, il ne prévoit pas le regroupement des partis. Plusieurs clients avec un tel système implémenté se sont plaints des résultats de la planification de la compression. Par exemple, souvent dans la pratique pendant la compression, la situation suivante s'est produite: 100 pièces. il est prévu de déplacer les marchandises restantes d'une cellule à une autre cellule, où se trouve 1 pc. bien qu'il soit optimal en termes de temps de faire le contraire.

De plus, la fonctionnalité de compression des marchandises résiduelles dans les cellules est déclarée dans de nombreux systèmes WMS étrangers, mais, malheureusement, nous n'avons pas de véritable retour sur l'efficacité des algorithmes (c'est un secret commercial), ni encore plus sur la profondeur de leur logique (logiciel propriétaire avec code fermé) nous n'en avons pas, donc nous ne pouvons pas juger.

Recherche d'un modèle mathématique d'un problème

Afin de concevoir des algorithmes de haute qualité pour résoudre un problème, il est d'abord nécessaire de formuler clairement ce problème mathématiquement, ce que nous ferons.

Il y a beaucoup de cellules $$$J$ dans lequel les restes de certains biens. De plus, ces cellules seront appelées cellules donneuses. Nous dénotons $$$w_j$ volume de marchandises dans la cellule $$$$ j$ $.

Il est important de dire qu'un seul produit d'un envoi, ou de plusieurs envois, précédemment regroupés en cluster (lire l' article précédent ) peut participer à la procédure de compression, ce qui est dû aux spécificités du stockage et du stockage des marchandises. Pour différents produits ou différents groupes de lots, une procédure de compression distincte doit être lancée.

Il y a beaucoup de cellules $$$I$ dans lequel les résidus des cellules donneuses peuvent potentiellement être placés. Ces cellules seront appelées cellules conteneurs. Il peut s'agir de cellules libres dans l'entrepôt ou de cellules donneuses provenant de $$$J$ . Toujours beaucoup $$$J$ est un sous-ensemble de $$$I$ .

Pour chaque cellule $$$i$ sur plusieurs $$$I$ limites de capacité fixées $$$d_i$ mesuré en dm3. Un dm3 est un cube avec des côtés de 10 cm Les produits stockés dans l'entrepôt sont assez grands, donc dans ce cas, une telle discrétisation suffit.

La matrice des distances les plus courtes $$$s_ {ij}$ en mètres entre chaque paire de cellules $$$(i, j)$ où $$$i$ et $$$j$ appartiennent aux ensembles $$$I$ et $$$J$ en conséquence.

Nous dénotons $$$S_ {ij}$ "Coûts" pour déplacer des marchandises de la cellule $$$i$ à la cellule $$$j$ . Nous dénotons $$$D_i$ "Coûts" pour choisir un conteneur $$$i$ pour y déplacer des résidus d'autres cellules. Comment exactement et dans quelles unités de mesure les valeurs seront-elles calculées $$$S_ {ij}$ et $$$D_i$ nous verrons plus loin (voir la section préparation des données d'entrée), il suffit maintenant de dire que ces quantités seront directement proportionnelles aux quantités $$$s_ {ij}$ et $$$d_i$ en conséquence.

Désigner par $$$x_ {ij}$ une variable prenant la valeur 1 si le reste de la cellule $$$j$ déplacer vers le conteneur $$$i$ et 0 sinon. Désigner par $$$y_i$ variable prenant la valeur 1 si le conteneur $$$i$ contient les restes du produit et 0 sinon.

La tâche est la suivante : il faut trouver autant de conteneurs $$$I ^ *$ et ainsi «attacher» les cellules donneuses aux conteneurs de cellules pour minimiser la fonction

$$

$$\ min {F} = \ sum _ {i \ in I, ~ j \ in J} ^ {} S_ {ij} \ cdot x_ {ij} + \ sum _ {i \ in I} ^ {} D_ { i} \ cdot y_ {i}$$

sous restrictions

$$

$$\ sum _ {j \ in J} ^ {} w_ {j} \ cdot x_ {ij} \ leq d_ {i} \ cdot y_ {i}, ~ pour ~ tout le monde ~ i \ in I$$

Au total, au cours du calcul de la solution du problème, nous nous efforçons de:

• premièrement, économisez la capacité de stockage;
• deuxièmement, faire gagner du temps aux commerçants.

La dernière restriction signifie que nous ne pouvons pas déplacer des marchandises vers un conteneur que nous n'avons pas sélectionné et que, par conséquent, nous n'avons pas «engagé de frais» pour leur choix. Cette restriction signifie également que le volume de marchandises transportées des cellules vers le conteneur ne doit pas dépasser la capacité du conteneur. Par la solution du problème, nous entendons beaucoup de conteneurs $$$I ^ *$ et des méthodes pour attacher des cellules donneuses à des conteneurs.

Cette formulation du problème d'optimisation n'est pas nouvelle et a été étudiée par de nombreux mathématiciens depuis le début des années 80 du siècle dernier. Dans la littérature étrangère, il existe 2 problèmes d'optimisation avec un modèle mathématique approprié: le problème de localisation des installations capacitées à source unique et le problème de localisation des installations capacitées à sources multiples (nous discuterons des différences entre les tâches ci-dessous). Il vaut la peine de dire que dans la littérature mathématique, les énoncés de ces deux problèmes d'optimisation sont formulés en termes de localisation des entreprises sur le terrain, d'où le nom «Facility Location». Pour la plupart, c'est un hommage à la tradition, car pour la première fois la nécessité de résoudre de tels problèmes combinatoires est venue du domaine de la logistique, pour la plupart, de la croissance militaro-industrielle dans les années 1950. En termes de localisation des entreprises, ces tâches sont formulées comme suit:

• Il existe un nombre fini de villes où il est possible de localiser des entreprises manufacturières (ci-après les villes manufacturières). Pour chaque ville manufacturière, les coûts d'ouverture d'une entreprise en son sein, ainsi qu'une restriction de la capacité de production de l'entreprise ouverte en son sein, sont fixés.
• Il existe un nombre fini de villes où les clients sont effectivement situés (ci-après dénommées villes clientes). Pour chacune de ces villes clientes, le volume de la demande de produits est fixé. Pour simplifier, nous supposons que le produit que les entreprises produisent et consomment des clients en est un.
• Pour chaque paire, la ville du fabricant et la ville du client, la valeur des coûts de transport pour la livraison du volume requis de produits du fabricant au client est définie.

Il est nécessaire de trouver dans quelles villes ouvrir des entreprises et comment attacher des clients à ces entreprises afin de:

• Le coût total de l'ouverture des entreprises et les coûts de transport étaient minimes;
• Le volume de la demande des clients attaché à toute entreprise ouverte n'a pas dépassé les capacités de production de cette entreprise.

Maintenant, il convient de mentionner la seule différence entre ces deux problèmes classiques:

• Problème de localisation des installations à source unique - le client n'est alimenté que par une seule entreprise ouverte;
• Problème de localisation des installations multi-sources capacitées - un client peut être alimenté par plusieurs entreprises ouvertes en même temps.

Une telle différence entre les deux problèmes à première vue est insignifiante, mais, en fait, conduit à une structure combinatoire complètement différente de ces problèmes et, par conséquent, à des algorithmes complètement différents pour les résoudre. Les différences entre les tâches sont illustrées dans la figure ci-dessous.


Fig.3. a) Problème de localisation des installations multi-sources


Fig.3. b) Problème de localisation des installations à source unique

Les deux tâches $$$NP$ sont difficiles, c'est-à-dire qu'il n'y a pas d'algorithme exact qui résoudrait un tel problème en temps polynomial à partir de la taille des données d'entrée. En termes plus simples, tous les algorithmes exacts pour résoudre le problème fonctionneront de façon exponentielle, bien que peut-être plus rapide qu'une recherche complète des options sur le front. Depuis la tâche $$$NP$ est difficile, nous ne considérerons alors que des heuristiques approximatives, c'est-à-dire des algorithmes qui calculeront de manière stable des solutions très proches de l'optimale et fonctionneront assez rapidement. S'il y a un intérêt pour une telle tâche, alors vous pouvez trouver ici une bonne critique en russe.

Si nous passons à la terminologie de notre problème de compression optimale des marchandises dans les cellules, alors:

• les villes clientes sont des cellules donneuses $$$J$ avec les restes de la marchandise,
• villes de fabrication - cellules conteneurs $$$I$ , dans lequel il est censé placer les restes d'autres cellules,
• frais de transport - temps $$$S_ {ij}$ magasinier pour déplacer le volume de marchandises de la cellule donneuse $$$j$ à la cellule conteneur $$$i$ ;
• le coût de l'ouverture d'une entreprise - le coût du choix d'un conteneur $$$D_i$ égal au volume de la cellule conteneur $$$i$ multiplié par un certain coefficient d'économie de volumes libres (la valeur du coefficient est toujours> 1) (voir la section préparation des données d'entrée).

Après avoir établi l'analogie avec les livraisons classiques bien connues du problème, il est nécessaire de répondre à la question importante dont dépend le choix de l'architecture de l'algorithme de la solution: le mouvement des résidus de la cellule donneuse n'est possible que dans un et un seul conteneur (Single-Source), ou le mouvement des résidus est possible dans plusieurs cellules de conteneur (multi-source)?

Il convient de noter qu'en pratique, les deux formulations du problème ont leur place. Nous donnons ci-dessous tous les avantages et les inconvénients de chacune de ces déclarations:
Tableau 1. Avantages et inconvénients des options à source unique et à sources multiples.

Étant donné que le nombre d'avantages pour l'option à source unique est plus élevé, et en tenant également compte du fait que plus le nombre de résidus dans les cellules donneuses est petit, plus la différence dans le degré de compacité de la compression calculée pour les deux versions du problème est petite, notre choix s'est porté sur le modèle Single- Source

Il convient de noter que la solution de l'option multi-source a également lieu. Il existe un grand nombre d'algorithmes efficaces pour le résoudre, dont la plupart se résument à résoudre un certain nombre de problèmes de transport. Il existe également non seulement des algorithmes efficaces, mais aussi des algorithmes élégants, par exemple .

Préparation des entrées

Avant de procéder à l'analyse et au développement d'un algorithme pour résoudre le problème, il est nécessaire de déterminer quelles données et sous quelle forme nous les soumettrons à l'entrée. Il n'y a pas de problème avec les volumes de marchandises laissées dans les cellules donneuses et la capacité des cellules conteneurs, car cela est trivial - ces valeurs seront mesurées en m3, mais avec les coûts d'utilisation du conteneur conteneur et le coût du déplacement de la matrice, ce n'est pas si simple!

Tout d'abord, nous considérons le calcul du coût de déplacement des marchandises d'une cellule donneuse à une cellule conteneur. Tout d'abord, il est nécessaire de déterminer dans quelles unités de mesure nous calculerons le coût du déménagement. Les deux options les plus évidentes sont les mètres et les secondes. Dans les compteurs "propres", le coût du déplacement est inutile. Nous montrons cela par l'exemple. Laissez la cellule $$$A$ situé au premier étage, cellule $$$À$ supprimé 30 mètres et est situé au deuxième niveau:

• Sortir $$$A$ dans $$$B$ plus coûteux que de passer de $$$B$ dans $$$A$ , car il est plus facile de descendre du deuxième étage (à 1,5-2 mètres du sol) que de le monter au deuxième, bien que la distance soit la même;
• Déplacez 1 pc. marchandises de la cellule $$$A$ dans $$$B$ Ce sera plus facile que de déplacer 10 pièces. du même produit, bien que la distance soit la même.

Les coûts de déplacement sont mieux pris en compte en quelques secondes, car cela vous permet de prendre en compte la différence de niveaux et la différence de quantité de marchandises transportées. Pour tenir compte des coûts du mouvement en secondes, il faut décomposer le fonctionnement du mouvement en composants élémentaires et prendre des mesures de temps pour chaque composant élémentaire.

Soit de la cellule $$$j$ se déplace $$$N_j$ pièces marchandises au conteneur $$$i$ . Soit $$$S_ {run}$ - la vitesse moyenne de l'employé dans l'entrepôt, mesurée en m / s. Soit $$$S_ {get}$ et $$$S_ {put}$ - des vitesses moyennes d'une seule exécution des opérations à prendre et à mettre, respectivement, pour le volume de marchandises égal à 4 dm3 (le volume moyen qu'un employé de l'entrepôt prend 1 fois pendant les opérations). Soit $$$H_ {get}$ et $$$H_ {put}$ la hauteur des cellules à partir desquelles les opérations sont effectuées prend et place en conséquence. Par exemple, la hauteur moyenne du premier étage (plancher) est de 1 m, le deuxième étage est de 2 m, etc. Ensuite, la formule pour calculer le temps total pour terminer l'opération de déplacement $$$T_ {ij}$ suivant:

$$

$$T_ {ij} = \ left (N_ {j} \ cdot \ frac {w_ {j}} {4} \ right) \ cdot S_ {get} \ cdot H_ {get} + s_ {ij} \ cdot S_ { exécuter} + \ gauche (N_ {j} \ cdot \ frac {w_ {j}} {4} \ droite) \ cdot S_ {put} \ cdot H_ {put}.$$

Le tableau 2 présente les statistiques du temps d'exécution de chaque opération élémentaire, collectées par le personnel de l'entrepôt, en tenant compte des spécificités des marchandises stockées.
Tableau 2. Temps moyen pour effectuer les opérations d'entrepôt

Avec la méthode de calcul du coût du déménagement décidé. Vous devez maintenant comprendre comment calculer le coût du choix d'une cellule de conteneur . Ici, tout est beaucoup, beaucoup plus compliqué qu'avec le coût du déménagement, car:

• premièrement, les coûts doivent être directement dépendants du volume de la cellule - il est préférable de mettre le même volume de résidus transférés des cellules donneuses dans un récipient d'un volume plus petit que dans un grand récipient, à condition qu'un tel volume rentre complètement dans les deux récipients . Ainsi, en minimisant le coût total du choix des conteneurs, nous nous efforçons d'économiser une capacité de stockage gratuite «rare» dans la zone de la zone de sélection pour effectuer les opérations ultérieures de placement des marchandises dans les cellules. La figure 4 montre les options de déplacement des résidus vers les grands et petits conteneurs et les conséquences de ces options pour le déplacement lors des opérations d'entrepôt ultérieures.
• deuxièmement, étant donné que nous devons minimiser les coûts totaux pour résoudre le problème initial, et c'est la somme du coût du déplacement et du coût du choix des conteneurs, les volumes de cellules en mètres cubes doivent en quelque sorte être liés aux secondes, ce qui est loin d'être trivial.

Fig. 4. Options pour déplacer les résidus dans des conteneurs de différentes capacités.

La figure 4 montre en rouge le volume de résidus qui ne tient plus dans le conteneur au deuxième stade du placement des marchandises suivantes.

Les exigences suivantes pour des solutions calculées au problème aideront à connecter les mètres cubes de coûts de conteneurs aux secondes de coûts de transport:

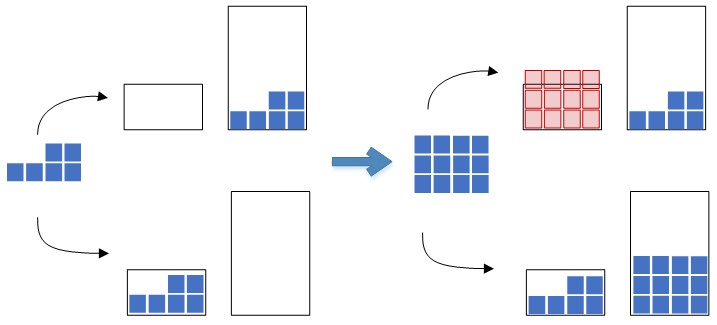
• Il est nécessaire que les résidus de la cellule donneuse soient transférés dans la cellule conteneur dans tous les cas, si cela réduit le nombre total de cellules conteneur dans lesquelles se trouvent les marchandises.
• Il est nécessaire de trouver un équilibre entre les volumes de conteneurs et le temps passé à se déplacer: par exemple, si la nouvelle solution au problème se compare à un gain de volume important et que la perte de temps est faible, vous devez en choisir un nouveau.

Commençons par la dernière exigence. Afin de préciser le mot ambigu «équilibre», nous avons mené une enquête auprès des employés de l'entrepôt afin de découvrir les éléments suivants. Qu'il y ait un volume de conteneur de cellules$$d 0 , dans lequel le mouvement des restes de marchandises des cellules donneuses est affecté et la durée totale de ce mouvement est$d_0$$$$T_0$ . Supposons qu'il existe plusieurs options alternatives pour placer la même quantité de marchandises provenant des mêmes cellules de donneurs dans d'autres conteneurs, où chaque emplacement a ses propres notes $$$d_1$ où $$$d_1$ < $$$d_0$ et $$$T_1$ où $$$T_1$ > $$$T_0$ .

La question est: quel est le gain minimum en volume $$d 0 - d 1 est acceptable, pour une valeur donnée de perte de temps$d_0-d_1$$$$T_1-T_0$ ?Illustrons par un exemple. Initialement, les résidus devaient être placés dans un conteneur de 1000 dm3 (1 m3) et le temps de trajet était de 70 secondes. Il est possible de placer les résidus dans un autre conteneur de 500 dm3 et un temps de 130 secondes. Question: sommes-nous prêts à consacrer 60 secondes supplémentaires au temps du commerçant pour déménager afin d'économiser 500 dm3 de volume gratuit? Basé sur une enquête auprès des employés de l'entrepôt, le tableau suivant a été compilé.


Fig. 5. Diagramme de la dépendance des économies de volume minimales autorisées sur l'augmentation de la différence de temps de fonctionnement.

Autrement dit, si les coûts de temps supplémentaires sont de 40 secondes, nous sommes prêts à les dépenser uniquement lorsque le gain de volume est d'au moins 500 dm3. Malgré le fait qu'une légère non-linéarité est observée dans la dépendance, pour simplifier les calculs ultérieurs, nous supposons que la dépendance entre les quantités est linéaire et est décrite par l'inégalité

$$

$$\frac{d_{0}-d_{1}}{10} \geq T_{1}-T_{0}$$

Dans la figure ci-dessous, nous considérons les méthodes suivantes pour placer des marchandises dans des conteneurs.


Fig. 6. Option (a): 2 conteneurs, volume total 400 dm3, durée totale 150 sec.

. 6. (b): 2 , 600 3, 190 .

Fig. 6. Option (s): 1 conteneur, volume total 400 dm3, durée totale 200 sec.

L'option (a) du choix des conteneurs est plus préférable que l'option initiale, car l'inégalité tient: (800-400) / 10> = 150-120, ce qui implique 40> = 30. L'option (b) est moins préférable que l'option d'origine , puisque l'inégalité ne tient pas: (800-600) / 10> = 190-150, ce qui implique 20> = 40. Mais l'option (c) ne rentre pas dans cette logique! Considérez cette option plus en détail. D'une part, l'inégalité (800-400) / 10> = 200-120, ce qui signifie que l'inégalité 40> = 80 n'est pas remplie, ce qui indique que le gain de volume ne vaut pas une si grosse perte de temps.

Mais d'autre part, dans cette option (c), nous réduisons non seulement le volume total occupé, mais également le nombre de cellules occupées, qui est la première des deux exigences importantes pour les solutions calculées aux problèmes énumérés ci-dessus. De toute évidence, pour que cette exigence commence à être remplie, il est nécessaire d'ajouter une constante positive au côté gauche de l'inégalité $$$Const$ , et une telle constante ne doit être ajoutée que lorsque le nombre de conteneurs diminue. Rappelez-vous que $$$y_i$ Est une variable égale à 1 lorsque le conteneur $$$i$ sélectionné et 0 lorsque le conteneur $$$i$ non sélectionné. Dénoter $$$I_0$ - de nombreux conteneurs dans la solution d'origine et $$$I_1$ - Beaucoup de conteneurs dans la nouvelle solution. De manière générale, la nouvelle inégalité ressemblera à ceci:

$$

$$\ sum _ {i \ in I_ {0}} ^ {} \ frac {d_ {i}} {10} + Const \ cdot \ sum _ {i \ in I_ {0}} ^ {} y_ {i} - \ left (\ sum _ {i \ in I_ {1}} ^ {} \ frac {d_ {i}} {10} + Const \ cdot \ sum _ {i \ in I_ {1}} ^ {} y_ {i} \ droite) \ geq T_ {1} -T_ {0}$$

En transformant l'inégalité ci-dessus, on obtient

$$

$$\ sum _ {i \ in I_ {0}} ^ {} \ frac {d_ {i}} {10} + Const \ cdot \ sum _ {i \ in I_ {0}} ^ {} y_ {i} + T_ {0} \ geq \ sum _ {i \ in I_ {1}} ^ {} \ frac {d_ {i}} {10} + Const \ cdot \ sum _ {i \ in I_ {1}} ^ {} y_ {i} + T_ {1}$$

Sur cette base, nous avons une formule pour calculer le coût total $$$F_k$ une solution au problème:

$$

$$F_ {k} = \ sum _ {i \ in I_ {k}} ^ {} \ frac {d_ {i}} {10} + Const \ cdot \ sum _ {i \ in I_ {k}} ^ {{ } y_ {i} + T_ {k}.$$

Mais maintenant, la question se pose : quelle valeur une telle constante devrait-elle avoir? $$$Const$ ? Il est évident que sa valeur doit être suffisamment grande pour que la première exigence de solution du problème soit toujours remplie. Vous pouvez bien sûr prendre une valeur constante égale à 10 ³ ou 10 ⁶ , mais je voudrais éviter de tels "nombres magiques". Si nous considérons les spécificités des opérations d'entrepôt, nous pouvons calculer plusieurs estimations numériques bien fondées de l'ampleur d'une telle constante.

Soit $$$S_ {max}$ - la distance maximale entre les cellules de l'entrepôt d'une zone ABC, égale dans notre cas à 100 m. $$$d_ {max}$ - le volume maximum du conteneur de cellules dans l'entrepôt, égal dans notre cas à 1000 dm3.

La première façon de calculer la valeur $$$Const$ . Considérez la situation où il y a 2 conteneurs au premier niveau dans lesquels les marchandises sont déjà physiquement situées, c'est-à-dire qu'elles sont elles-mêmes des cellules donneuses, et que le coût du déplacement des marchandises vers les mêmes cellules est naturellement de 0. Il est nécessaire de trouver une telle valeur constante $$$Const$ dans lequel il serait avantageux de toujours déplacer les résidus du conteneur 1 vers le conteneur 2. Remplacer les valeurs $$$S_ {max}$ et $$$d_ {max}$ dans l'inégalité ci-dessus, on obtient:

$$

$$\ frac {d_ {max}} {10} + Const \ geq S_ {max} \ cdot s_ {run} + \ frac {d_ {max}} {4} \ left (s_ {get} + s_ {put} \ droite),$$

ce qui suit

$$

$$Const \ geq S_ {max} \ cdot s_ {run} + d_ {max} \ left (\ frac {s_ {get} + s_ {put}} {4} - \ frac {1} {10} \ right) .$$

En substituant les valeurs du temps d'exécution moyen des opérations élémentaires dans la formule ci-dessus, on obtient

$$

$$Const \ geq 100 \ cdot 1.5 + 1000 \ left (\ frac {9} {10} \ right) \ rightarrow Const \ geq 1050.$$

La deuxième façon de calculer la valeur $$$Const$ . Considérons une situation où il y a $$$N$ cellules donneuses à partir desquelles il est prévu de déplacer les marchandises dans le conteneur 1. Noter $$$S_ {1j}$ - distance de la cellule donneuse $$$j$ au conteneur 1. Il y a aussi le conteneur 2, dans lequel il y a déjà des marchandises, et dont le volume vous permet d'accueillir le reste $$$N$ les cellules. Pour simplifier, nous supposerons que le volume de marchandises transportées des cellules du donneur aux conteneurs est identique et égal $$$d_ {max} / N$ . Il est nécessaire de trouver une telle valeur constante $$$Const$ à laquelle le placement de tous les résidus de $$$N$ les cellules du conteneur 2 seraient toujours plus rentables que de les placer dans des conteneurs différents:

$$

$$2 \ cdot \ frac {d_ {max}} {10} +2 \ cdot Const + N \ left (S_ {1j} \ cdot s_ {run} + \ frac {d_ {max}} {4 \ cdot N} \ gauche (s_ {get} + s_ {put} \ right) \ right) \ geq \ qquad \ qquad \ qquad \ qquad \ qquad \\ \ qquad \ qquad \ qquad \ qquad \ qquad \ frac {d_ {max}} { 10} + Const + N \ cdot \ left (S_ {max} \ cdot s_ {run} + \ frac {d_ {max}} {4 \ cdot N} \ left (s_ {get} + s_ {put} \ right ) \ droite).$$

Transformer l'inégalité que nous obtenons

$$

$$\ frac {d_ {max}} {10} + Const + N \ cdot S_ {1j} \ cdot s_ {run} \ geq N \ cdot S_ {max} \ cdot s_ {run} \ rightarrow Const \ geq N \ cdot s_ {run} \ left (S_ {max} -S_ {1j} \ right) - \ frac {d_ {max}} {10}.$$

Afin de "renforcer" la valeur de la quantité $$$Const$ , nous supposons que $$$S_ {1j}$ = 0. Le nombre moyen de cellules qui sont généralement impliquées dans le processus de compression des soldes de stock est de 10. En substituant les valeurs connues des quantités, nous avons la valeur constante suivante

$$

$$Const \ geq 10 \ cdot 1.5 \ cdot 100- \ frac {1000} {10} \ rightarrow Const \ geq 1400.$$

Nous prenons la plus grande valeur calculée pour chaque option, ce sera la valeur de $$$Const$ pour des paramètres d'entrepôt donnés. Maintenant, pour être complet, nous écrivons la formule de calcul des coûts totaux $$$F_k$ pour une solution réalisable $$$k$ :

$$

$$F_ {k} = \ sum _ {i \ in I_ {k}} ^ {} \ frac {d_ {i}} {10} +1400 \ cdot \ sum _ {i \ in I_ {k}} ^ {{ } y_ {i} + T_ {k}.$$

Maintenant, après tous les efforts titanesques pour convertir les données d'entrée, nous pouvons dire que toutes les données d'entrée sont converties sous la forme souhaitée et sont prêtes à être utilisées dans l'algorithme d'optimisation.

Conclusion

Comme le montre la pratique, la complexité et l'importance de la préparation et de la conversion des données d'entrée pour l'algorithme sont souvent sous-estimées. Dans cet article, nous avons spécifiquement accordé beaucoup d'attention à cette étape afin de montrer que seules les données d'entrée préparées de manière qualitative et sage peuvent rendre les décisions calculées par l'algorithme vraiment précieuses pour le client. Oui, il y avait beaucoup de conclusions sur les formules, mais on vous prévenait avant le kat :)

Dans le prochain article, nous arriverons enfin à ce à quoi pensaient les 2 publications précédentes - l'algorithme d'optimisation discrète.

Préparé un article
Roman Shangin, programmeur, département des projets,
Entreprise First Bit, Chelyabinsk