Mathématiques discrètes pour WMS: algorithme de compression des marchandises dans les cellules (partie 2)

Dans l'article, nous décrirons comment nous avons développé un algorithme pour la compression optimale des marchandises restantes dans les cellules. Nous vous expliquerons comment choisir les métaheuristiques nécessaires de l'environnement du zoo cadre: recherche taboue, algorithme génétique, colonie de fourmis, etc.

Nous effectuerons une expérience de calcul pour analyser le temps de fonctionnement et la précision de l'algorithme. Nous résumons et résumons la précieuse expérience acquise dans la résolution de ce problème d’optimisation et de mise en œuvre de «technologies intelligentes» dans les processus commerciaux du client.

L'article sera utile à ceux qui mettent en œuvre des technologies intelligentes, travaillent dans l'entrepôt ou l'industrie de la logistique de production, ainsi qu'aux programmeurs qui s'intéressent aux applications mathématiques en optimisation des affaires et des processus dans l'entreprise.

Partie introductive

Cette publication poursuit la série d'articles dans lesquels nous partageons notre expérience réussie dans la mise en œuvre d'algorithmes d'optimisation dans les processus d'entrepôt. Publications précédentes:

• algorithme de regroupement des envois en stock.
• un algorithme de compression des marchandises résiduelles dans les cellules (partie 1).

Comment lire un article. Si vous lisez les articles précédents, vous pouvez immédiatement passer au chapitre "Développement d'un algorithme pour résoudre le problème", sinon, la description du problème à résoudre dans le spoiler ci-dessous.

Développement d'un algorithme pour résoudre le problème

Avant de procéder à une description directe de l'algorithme d'optimisation, il est nécessaire de parler des principaux critères de développement d'un tel algorithme, qui ont été définis dans le cadre du projet de mise en œuvre du système WMS .

• Premièrement, l'algorithme doit être facile à comprendre . Ceci est une exigence naturelle, car il est supposé que l’algorithme sera pris en charge et développé par le service informatique du client à l’avenir, ce qui est souvent loin des subtilités mathématiques et de la sagesse.
• Deuxièmement, l'algorithme doit être rapide . Presque toutes les marchandises de l'entrepôt sont impliquées dans la procédure de compression (environ 3 000 articles) et pour chaque produit, il est nécessaire de résoudre un problème de dimension d'environ 10x100.
• Troisièmement, l'algorithme doit calculer des solutions proches de l'optimale .
• Quatrièmement, le temps nécessaire pour concevoir, mettre en œuvre, déboguer, analyser et tester en interne l'algorithme est relativement court. Il s'agit d'une exigence essentielle, car le budget du projet , y compris pour cette tâche, était limité .

Il vaut la peine de dire qu'à ce jour, les mathématiciens ont développé de nombreux algorithmes efficaces pour résoudre le problème du problème de localisation des installations à source unique. Considérez les principales variétés des algorithmes disponibles.

Certains des algorithmes les plus efficaces sont basés sur l'approche de la relaxation dite de Lagrange. En règle générale, ce sont des algorithmes assez complexes qui sont difficiles à comprendre pour une personne qui n'est pas plongée dans les subtilités de l'optimisation discrète. La «boîte noire» aux algorithmes complexes mais efficaces de relaxation Lagrange du client ne convenait pas.

Il existe des métaheuristiques assez efficaces (ce qui est des métaheuristiques lues ici , ce qui est des heuristiques lues ici ), par exemple, des algorithmes génétiques, des algorithmes de recuit simulé, des algorithmes de colonie de fourmis, des algorithmes de recherche tabous et autres (un aperçu de ces métaheuristiques en russe peut être trouvé ici ). Mais de tels algorithmes ont déjà satisfait le client, car:

• Capable de calculer des solutions à des problèmes très proches de l'optimale.
• Assez simple à comprendre, support supplémentaire, débogage et raffinement.
• Ils peuvent rapidement calculer une solution à un problème.

Il a été décidé d'utiliser des métaheuristiques. Il ne restait plus qu'à choisir un «cadre» parmi le grand «zoo» de métaheuristiques célèbres pour résoudre le problème de localisation des installations à source unique. Après avoir examiné un certain nombre d'articles qui analysaient l'efficacité de diverses métaheuristiques, notre choix s'est porté sur l'algorithme GRASP, car en comparaison avec d'autres métaheuristiques, il a montré des résultats plutôt bons sur la précision des solutions calculées au problème, était l'un des plus rapides et, surtout, il avait le plus simple et une logique transparente.

Le schéma de l'algorithme GRASP en relation avec la tâche de problème de localisation des installations à source unique est décrit en détail dans l' article . Le schéma général de l'algorithme est le suivant.

• Étape 1. Générez une solution réalisable au problème par un algorithme aléatoire gourmand.
• Étape 2. Améliorez la solution résultante à l'étape 1 en utilisant l'algorithme de recherche locale dans un certain nombre de quartiers.
• Si la condition d'arrêt est satisfaite, complétez l'algorithme, sinon passez à l'étape 1. La solution avec le coût total le plus bas parmi toutes les solutions trouvées sera le résultat de l'algorithme.

La condition d'arrêt de l'algorithme peut être une simple restriction du nombre d'itérations ou une restriction du nombre d'itérations sans amélioration de la solution.


Examinons plus en détail le fonctionnement de l' algorithme aléatoire gourmand au stade 1. On pense qu'au début, pas un seul conteneur de cellules n'est sélectionné.

• Étape 1. Pour chaque cellule de conteneur non sélectionnée actuellement, la valeur est calculée $$$F_ {i} ^ {'}$ formule de coût
  

  $$

  $$F_ {i} ^ {'} = \ frac {F_ {i}} {N},$$
  où $$$F_ {i} ^ {'}$ - le montant du coût du choix d'un conteneur $$$i$ et les coûts totaux pour le transport de marchandises $$$N$ cellules qui ne sont pas encore attachées à un conteneur dans le conteneur $$$i$ . Ces $$$N$ les cellules sont sélectionnées de manière à ce que le volume total des marchandises ne dépasse pas la capacité du conteneur $$$i$ . Les cellules donneuses sont sélectionnées séquentiellement pour se déplacer dans un conteneur conteneur $$$i$ par ordre d'augmentation du coût de déplacement de la quantité de marchandises dans le conteneur $$$i$ . La sélection des cellules est effectuée jusqu'à ce que la capacité du conteneur soit dépassée.
• Étape 2. Ensemble formé $$$R$ conteneurs avec valeur de fonction $$$F$ ne dépassant pas la valeur seuil $$$\ min (F) \ cdot (1 + a)$ où $$$a$ dans notre cas, il est de 0,2.
• Étape 3. Au hasard de l'ensemble $$$R$ le conteneur est sélectionné $$$i$ . $$$N$ cellules précédemment sélectionnées dans le conteneur $$$i$ à l'étape 1, ils sont finalement affectés à un tel conteneur et ne participent plus aux calculs de l'algorithme gourmand.
• Étape 4. Si toutes les cellules donneuses sont affectées à des conteneurs, l'algorithme gourmand arrête son travail, sinon il revient à l'étape 1.

L'algorithme randomisé à chaque itération tente de construire la solution de telle manière qu'il y ait un équilibre entre la qualité des solutions qu'il construit, ainsi que leur diversité. Ces deux exigences pour le démarrage des décisions sont les conditions clés pour le bon fonctionnement de l'algorithme, car:

• si les solutions sont de mauvaise qualité, l'amélioration ultérieure de l'étape 2 ne donnera pas de résultats significatifs, car même en améliorant la mauvaise solution, on se retrouvera très souvent avec les mêmes solutions de mauvaise qualité;
• Si toutes les solutions sont bonnes, mais les mêmes, alors les procédures de recherche locale convergeront vers la même solution, ce n'est en aucun cas la solution optimale. Cet effet est appelé atteindre un minimum local et doit toujours être évité.

Une fois la solution «de départ» construite à l'étape 1, l'algorithme passe à l'étape 2, où l'amélioration d'une telle solution trouvée est effectuée, où l'amélioration signifie naturellement une réduction du coût total. La logique de l'algorithme de recherche locale à l'étape 2 est la suivante.

• Étape 1. Pour la solution actuelle $$$S$ toutes les solutions "voisines" sont construites selon une sorte de quartier $$$N1$ , $$$N2$ , ..., $$$N5$ et pour chaque solution "voisine", la valeur des coûts totaux est calculée.
• Étape 2. Si parmi les solutions voisines il y avait une meilleure solution $$$S1$ que la solution d'origine $$$S$ alors $$$S$ supposé égal $$$S1$ et l'algorithme passe à l'étape 1. Sinon, si parmi les solutions voisines il n'y avait pas de meilleure solution que la solution d'origine, la vue du quartier passe à une nouvelle non précédemment prise en compte et l'algorithme passe à l'étape 1. Si toutes les vues disponibles du quartier sont prises en compte, mais ont échoué trouver une solution meilleure que l'original, l'algorithme termine son travail.

Les vues de l'environnement sont sélectionnées séquentiellement dans la pile suivante: $$$N1$ , $$$N2$ , $$$N3$ , $$$N4$ , $$$N5$ . Les vues sur les environs sont divisées en 2 types: le premier type (quartier $$$N1$ , $$$N2$ , $$$N3$ ), où de nombreux conteneurs ne changent pas, mais seules les options de fixation des cellules du donneur changent; deuxième type (quartier $$$N4$ , $$$N5$ ), où non seulement les options pour attacher des cellules aux conteneurs changent, mais aussi les nombreux conteneurs eux-mêmes.

Nous dénotons $$$| J |$ - le nombre d'éléments dans l'ensemble $$$J$ . Les figures ci-dessous illustrent les options pour les quartiers du premier type .


Fig. 7. Quartier $$$N1$

Quartier $$$N1$ (ou quartier de décalage ): contient toutes les options pour résoudre le problème qui diffèrent de l'original en modifiant l'attachement d'une seule cellule donneuse au conteneur. La taille du quartier n'est plus $$$| J |$ les options.


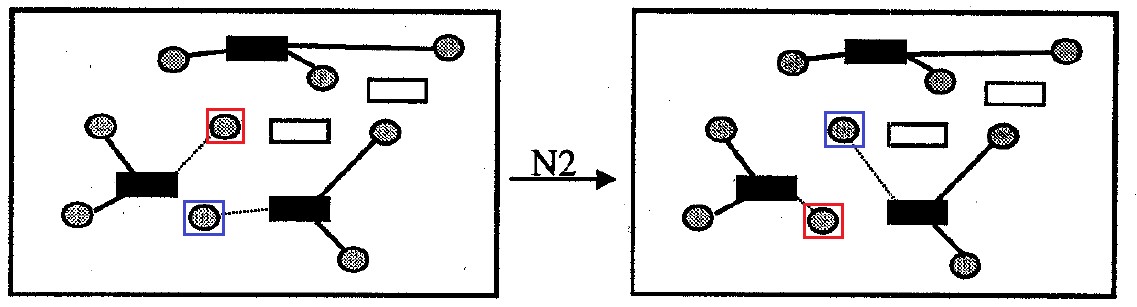Fig. 8. Quartier $$$N2$


Quartier $$$N2$ (ou échange de voisinage): contient toutes les options pour résoudre le problème qui diffèrent de l'original par l'échange mutuel d'attachement aux conteneurs pour une paire de cellules donneuses. La taille du quartier n'est plus $$$| J | ^ 2$ les options.


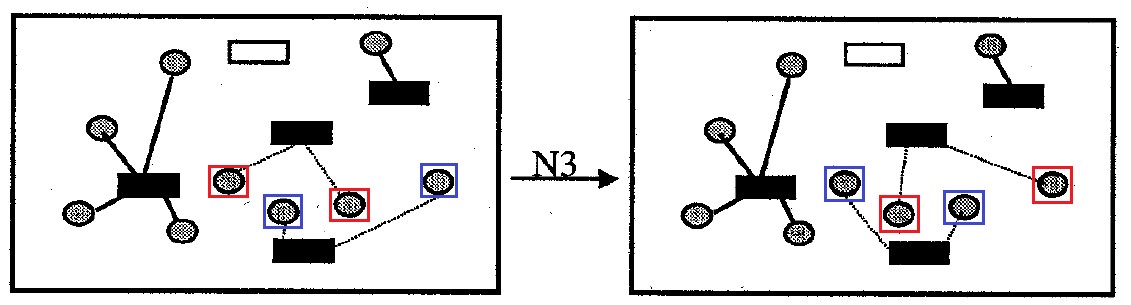Fig. 9. Quartier $$$N3$

Quartier $$$N3$ : contient toutes les options pour résoudre le problème, qui diffèrent de l'original par le remplacement mutuel de la fixation de toutes les cellules pour une paire de conteneurs. La taille du quartier n'est plus $$$| I |$ les options.

Le deuxième type de quartiers est considéré comme un mécanisme de «diversification» des décisions, lorsqu'il est déjà impossible d'obtenir des améliorations en recherchant les quartiers «proches» du premier type.


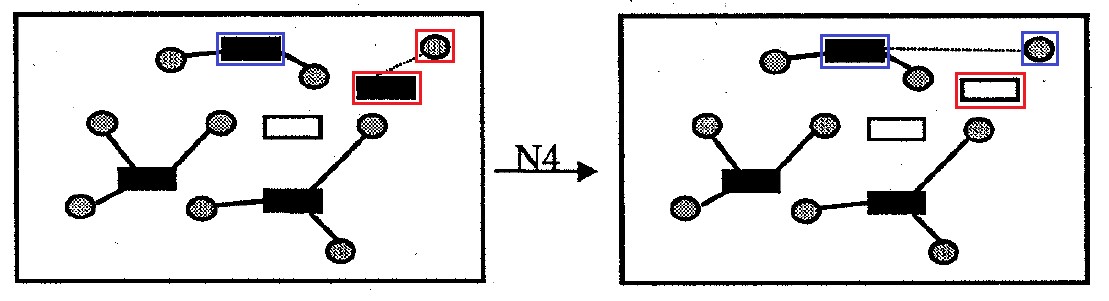Fig. 10. Quartier $$$N4$

Quartier $$$N4$ : contient toutes les options pour résoudre le problème qui diffèrent de l'original en supprimant une cellule de conteneur de la solution. Les cellules donneuses qui étaient attachées à un tel conteneur qui a été retiré de la solution sont attachées à d'autres conteneurs afin de minimiser le montant des frais de transport et la pénalité pour dépassement de la capacité du conteneur. La taille du quartier n'est plus $$$| I |$ les options.


Fig. 11. Quartier $$$N5$

Quartier $$$N5$ : contient toutes les options pour résoudre le problème qui diffèrent de l'original en détachant les cellules d'un conteneur et en attachant ces cellules à un autre conteneur vide pour une paire arbitraire de conteneurs. La taille du quartier n'est plus $$$| I | ^ 2$ les options.

Les auteurs de l'article disent que, sur la base des résultats d'expériences de calcul, la meilleure option est de rechercher d'abord les quartiers "proches" du premier type, puis de rechercher les quartiers "éloignés".

A noter que les auteurs de l'article recommandent d'effectuer une recherche à proximité sans tenir compte des restrictions de capacité de chaque conteneur. Au lieu de cela, si la capacité du conteneur est dépassée, ajoutez au coût total de la solution une quantité positive de «fine», ce qui nuira à l'attractivité d'une telle solution par rapport à d'autres solutions. La seule restriction concerne le volume total des conteneurs, c'est-à-dire que le volume total des marchandises transportées depuis les cellules des donneurs ne doit pas dépasser la capacité totale des conteneurs. Cette suppression des restrictions est effectuée car si les restrictions sont prises en compte, alors le quartier ne contiendra souvent pas une seule solution acceptable et l'algorithme de recherche local terminera son travail immédiatement après son démarrage, sans apporter aucune amélioration. La figure 12 montre un exemple d'une opération de recherche locale sans tenir compte des restrictions sur la capacité de chaque conteneur.


Fig. 12. Le travail de recherche locale sans tenir compte des restrictions de capacité de chaque conteneur

Dans cette figure, il est supposé que les résidus rouges et verts de certaines cellules donneuses ne sont pas bénéfiques pour se déplacer vers un autre conteneur, sauf le second. Cela signifie qu'une amélioration supplémentaire de la solution est impossible, car toute autre nouvelle solution réalisable au problème, où les restrictions de capacité sont respectées, sera pire que l'original en termes de coûts de transport. Comme vous pouvez le voir, l'algorithme pour 2 itérations construit une solution réalisable beaucoup mieux que l'original, malgré le fait que la première itération crée une solution invalide avec une capacité excédentaire.

Notez que cette approche consistant à introduire une «pénalité» pour l'inadmissibilité d'une solution est assez courante dans l'optimisation discrète et est souvent utilisée dans des algorithmes tels que les algorithmes génétiques, la recherche taboue, etc.

Une fois l'algorithme de recherche locale terminé, si la solution trouvée est toujours inacceptable, c'est-à-dire que les limites de capacité des conteneurs ont été dépassées quelque part, nous devons amener la solution trouvée sous une forme acceptable, où toutes les restrictions sur la capacité des conteneurs sont respectées. L'algorithme pour résoudre l'irrecevabilité de la solution est le suivant.

• Étape 1. Effectuez une recherche locale sur les quartiers de changement et d' échange . Dans ce cas, la transition n'est effectuée que dans les décisions qui réduisent précisément le montant de l '«amende». Si la réduction de la pénalité n'est pas possible, alors une solution avec des coûts totaux inférieurs est choisie. Si aucune amélioration supplémentaire par recherche locale n'est possible, passez à l'étape 2, sinon, si la solution résultante est valide, complétez l'algorithme.
• Étape 2. Si la solution est toujours inacceptable, alors de chaque conteneur où il y avait un excédent de capacité, les cellules donneuses sont détachées par ordre d'augmentation du volume de marchandises jusqu'à ce que la restriction de capacité soit respectée. Pour de telles cellules détachées, toutes les étapes de l'algorithme, en commençant par la première, sont répétées, malgré le fait que l'ensemble des conteneurs sélectionnés disponibles et la manière d'y attacher les cellules restantes sont fixes et ne peuvent pas être modifiés. Notez qu'une telle étape 2, comme le montre l'expérience de calcul, doit être effectuée extrêmement rarement.

Expérience informatique et analyse de l'efficacité des algorithmes

L'algorithme GRASP a été implémenté à partir de zéro en C ++ , car nous n'avons pas trouvé le code source de l'algorithme décrit dans l' article . Le code du programme a été compilé à l'aide de g ++ avec l'option d'optimisation -O2.

Le code de projet Visual Studio est disponible sur GitHub . La seule chose que le client a demandé était de supprimer certaines des procédures de recherche locale les plus complexes pour des raisons de propriété intellectuelle, de secrets commerciaux, etc.

Dans l' article qui décrit l'algorithme GRASP, sa haute efficacité a été mentionnée, où par efficacité, on entend qu'il calcule de manière stable des solutions très proches de l'optimale, et qu'il fonctionne assez rapidement. Afin de vérifier l'efficacité réelle d'un tel algorithme GRASP, nous avons mené notre propre expérience de calcul. Les données d'entrée du problème ont été générées par nous au hasard avec une distribution uniforme. Les solutions calculées par l'algorithme ont été comparées aux solutions optimales, qui ont été calculées par l'algorithme exact proposé dans l' article . Les sources d'un tel algorithme exact sont disponibles gratuitement sur GitHub par référence . La dimension de la tâche, par exemple, 10x100 signifie que nous avons 10 cellules donneuses et 100 cellules conteneurs.

Les calculs ont été effectués sur un ordinateur personnel présentant les caractéristiques suivantes: CPU 2,50 GHz, Intel Core i5-3210M, 8 Go de RAM, système d'exploitation Windows 10 (x64).
Tableau 3. Comparaison du temps de fonctionnement de l'algorithme GRASP et de l'algorithme exact

Comme le montre le tableau 3, l'algorithme GRASP calcule vraiment près des solutions optimales, et avec une augmentation de la dimension du problème, la qualité des solutions de l'algorithme se détériore légèrement. Les résultats de l'expérience montrent également que l'algorithme GRASP est assez rapide, par exemple, il résout un problème de dimension 10x100 en moyenne en 0,5 seconde. Il convient de mentionner à la fin que les résultats de notre expérience de calcul sont cohérents avec les résultats de l' article .

Exécution de l'algorithme en production

Après que l'algorithme a été développé, débogué et testé dans une expérience de calcul, le moment est venu de le mettre en service. L'algorithme a été implémenté en C ++ et a été placé dans une DLL qui s'est connectée à l'application 1C en tant que composant externe de type natif. Découvrez les composants externes 1C et comment les développer et les connecter correctement à l'application 1C ici . Dans le programme «1C: Warehouse Management 3», un formulaire de traitement a été développé dans lequel l'utilisateur peut démarrer la procédure de compression des résidus avec les paramètres dont il a besoin. Une capture d'écran du formulaire est présentée ci-dessous.


Fig.13. La forme de la procédure de «compression» des soldes dans l'annexe 1C: Gestion des entrepôts 3

L'utilisateur peut sélectionner les paramètres de compression des résidus sous la forme:

• Mode de compression: avec clustering de lots (voir le premier article) et sans lui.
• Entrepôt, dans les cellules dont il est nécessaire d'effectuer la compression. Dans une pièce, il peut y avoir plusieurs entrepôts pour différentes organisations. Une telle situation était avec notre client.
• En outre, l'utilisateur peut ajuster de manière interactive la quantité de marchandises transférées de la cellule donneuse au conteneur et supprimer l'article de la liste pour la compression, s'il souhaite pour une raison quelconque qu'il ne participe pas à la procédure de compression.

Conclusion

À la fin de l'article, je veux résumer l'expérience acquise à la suite de l'introduction d'un tel algorithme d'optimisation.

• . : , , . - :
  
  1. , ;
  2. .
• ( ), , . «», - . , , . , , , - , .
• , ( ), . , , . , . . , .
• :
  
  1. .
  2. .
  3. . , .
  4. . , . , , , , .
  5. , . ( ) . , .
  6. .

Et, je pense, la chose la plus importante. Le processus d'optimisation dans l'entreprise doit souvent suivre après l'achèvement du processus d'informatisation. L'optimisation sans informatisation préalable est de peu d'utilité , car il n'y a nulle part où obtenir des données et il n'y a nulle part où écrire les données de solution de l'algorithme. Je pense que la majorité des moyennes et grandes entreprises nationales ont fermé les besoins fondamentaux d'automatisation et d'informatisation et sont prêtes pour une optimisation plus fine des processus.

Par conséquent, nous pratiquons après la mise en œuvre du système d'information, que ce soit ERP, WMS, TMS, etc. faire un petit extra. des projets pour optimiser les processus identifiés lors de la mise en place du système d'information comme problématiques et importants pour le client. Je pense que c'est une pratique prometteuse qui va prendre de l'ampleur dans les années à venir.


, ,
, .