Etude du système de lévitation magnétique à contrôle modal

Ce matériel a été créé en vue de la défense passée du travail de qualification final du baccalauréat, en tenant compte de certains commentaires sur l'objet de contrôle. Le matériel est créé comme une réserve initiale pour une éventuelle thèse de maîtrise sur le même sujet.

Les systèmes de lévitation magnétique modernes sont de plus en plus utilisés: trains de voyageurs à grande vitesse, isolation des mécanismes sensibles aux vibrations, paliers magnétiques, lévitation du métal en fusion dans les fours à induction, ainsi que lévitation des billettes métalliques. Récemment, l'effet de la lévitation magnétique est également utilisé dans les appareils ménagers.

L'application la plus importante a peut-être été trouvée dans les trains équipés d'un système de lévitation sur les supraconducteurs. Et cela est dû à des avantages tels qu'une plus grande fiabilité (en raison de l'absence de frottement), une consommation d'énergie relativement faible et la capacité de développer une vitesse élevée.

Cependant, en raison des équations de mouvement non linéaires de l'objet qui décrivent sa dynamique, il est difficile de reproduire le processus de contrôle de l'objet. Il s'agira de la position (distance) de l'objet par rapport à la marque zéro.

En bref, la lévitation magnétique est la position stable d'un objet à une certaine distance dans un champ gravitationnel, lorsque, en règle générale, l'accélération de la gravité est compensée par l'accélération de l'objet, qui est créée par un champ magnétique. Dans ce cas, une force de levage apparaît.

La lévitation magnétique est réalisée à l'aide de diamagnétiques, de systèmes à courants de Foucault et de supraconducteurs, ainsi qu'à l'aide de servomécanismes.

Dans l'article actuel (sous la coupe), nous considérerons le contrôle modal pour un système linéarisé de lévitation magnétique, ainsi que la mise en œuvre du contrôle modal pour un modèle non linéaire du système.

Modèle mathématique

Considérons un schéma de lévitation magnétique simple.

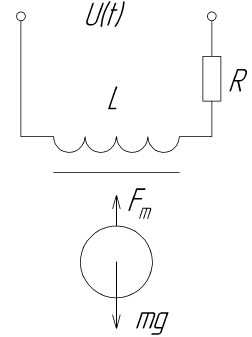
Ce diagramme montre un électroaimant qui interagit avec le champ magnétique de l'objet de contrôle, qui est un aimant permanent à bille. Grâce à un changement dans la force d'attraction de l'électro-aimant, l'effet de lévitation sera atteint.

Dans le travail final, un objet de second ordre a été considéré, où un composant important, le courant dans la bobine, n'était pas inclus dans le vecteur d'état. Cette fois, ce composant sera introduit.

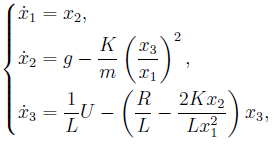
où $$$x_1$- position de l'objet;

$$$x_2$- le taux de variation de la position de l'objet;

$$$g$- accélération de la gravité;

$$$K$Est une constante;

$$$m$- masse de l'objet boule;

$$$x_3$- courant dans la bobine;

$$$L$- inductance de bobine;

$$$U$- tension d'entrée;

$$$R$- résistance active de la bobine.

Les valeurs de certaines des variables ci-dessus sont résumées dans un tableau.

Pour obtenir un modèle linéaire, il faut linéariser le système d'équations.

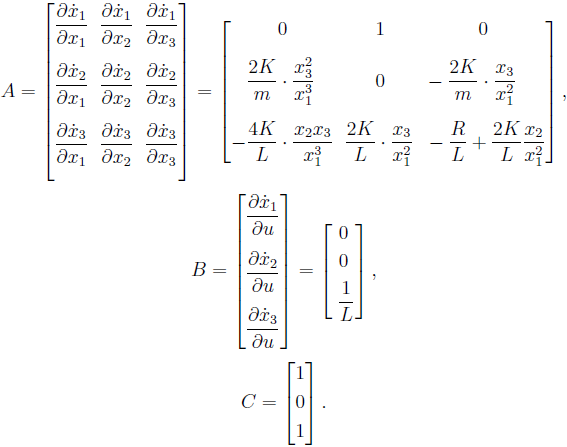
Vue matricielle $$$C$peut être justifiée par le fait que des variables vectorielles d'état comme la position ( $$$x_1$) et actuel ( $$$x_3$)

Sous cette forme, les matrices résultantes ne sont toujours pas adaptées à la modélisation. Pour ce faire, nous fixons les conditions initiales.

$$

$$x_1 ^ {\ left \ {0 \ right \}} = 0,005, ~ x_2 ^ {\ left \ {0 \ right \}} = 0.$$

$$

$$g - \ frac {K (x_3 ^ {\ left \ {0 \ right \}}) ^ 2} {m (x_1 ^ {\ left \ {0 \ right \}}) ^ 2} = 0$$

$$

$$x_3 ^ {\ left \ {0 \ right \}} = \ sqrt {\ frac {gm} {K}} x_1 ^ {\ left \ {0 \ right \}} = 0,063 ~ \ text {A}.$$

Remplacez maintenant les données obtenues et $$$x_3 ^ {\ gauche \ {0 \ droite \}}$ pour trouver la valeur du signal d'entrée à l'instant initial:

$$

$$U ^ {\ left \ {0 \ right \}} = \ left (R - \ frac {2Kx_2 ^ {\ left \ {0 \ right \}}} {(x_1 ^ {\ left \ {0 \ right \ }}) ^ 2} \ droite) x_3 ^ {\ gauche \ {0 \ droite \}} = Rx_3 ^ {\ gauche \ {0 \ droite \}} = 1,95 ~ \ texte {B}.$$

Modélisation

Vous pouvez maintenant synthétiser le contrôle. Pour la recherche, le package Matlab a été sélectionné. Voici le code pour obtenir les coefficients du régulateur par état:

g = 9.81; K = 0.659*10^-3; m = 0.0106; L = 0.109; R = 31.1; x10 = 0.005; x20 = 0; x30 = sqrt(g*m/K)*x10; u = R*x30; A = [0 1 0; 2*K*x30^2/(m*x10^3) 0 -2*K*x30/(m*x10^2); -4*K*x20*x30/(L*x10^3) 2*K*x30/(L*x10^2) -R/L+2*K*x20/(L*x10^2)]; B = [0; 0; 1/L]; C = [1 0 0]; W = ctrb(A, B); %   detW = det(W); poles = [-10 -10 -10]; %  K = acker(A, B, poles); %  system = ss(A - B*K, B, C, 0); %   figure(1) step(system) %   km = 1/dcgain(system); %   system_m = ss(A - B*K, B*km, C, 0); figure(2) step(system_m) 

Pour comprendre s'il est possible de synthétiser le contrôle pour le système résultant, vous devez connaître la matrice de contrôlabilité, par le déterminant dont la conclusion est tirée:

 >> detW detW = -7.5351e+07 

Le déterminant n'est pas nul; par conséquent, le système linéarisé est contrôlable.

Le vecteur des pôles est un vecteur qui contient les pôles souhaités du système linéarisé de lévitation magnétique.

Lors de l'application de l'effet de test sous la forme d'une seule étape, nous obtenons le résultat suivant:

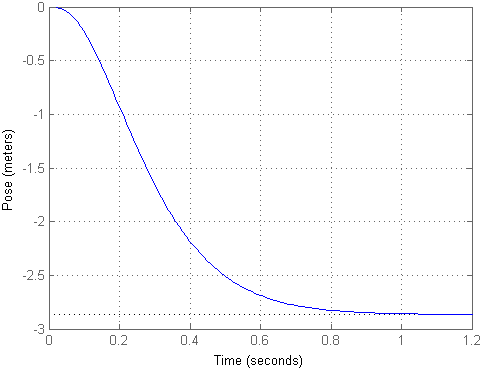
Comme vous pouvez le voir, il s'avère que l'objet a volé sur une assez grande distance avec peu d'impact, bien qu'il soit resté dans la même position. Pour que l'entrée corresponde à la sortie, nous pouvons calculer le facteur d'échelle km et multiplier par lui le signal d'entrée, ce qui a été réalisé dans le deuxième modèle. Ensuite, le processus de transition ressemblera à ceci:

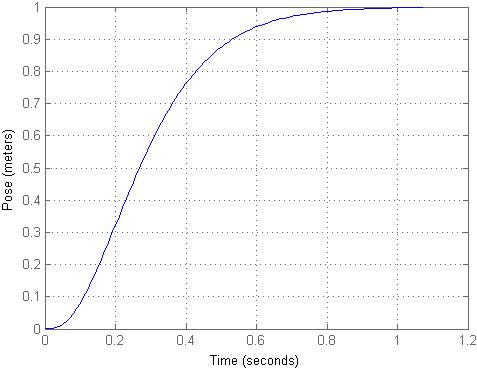
La position résultante est toujours idéale pour une telle installation. Pour l'instant, ignorons le courant et passons directement aux modèles Simulink, où nous considérons les choses restantes.

Nous mettons à l'échelle le signal d'entrée afin que les valeurs de sortie soient représentées de manière pratique en centimètres. Nous appliquons plusieurs actions de test à l'entrée pour vérifier à quoi ressemblent les transitoires dans le système, ainsi que le courant circulant.

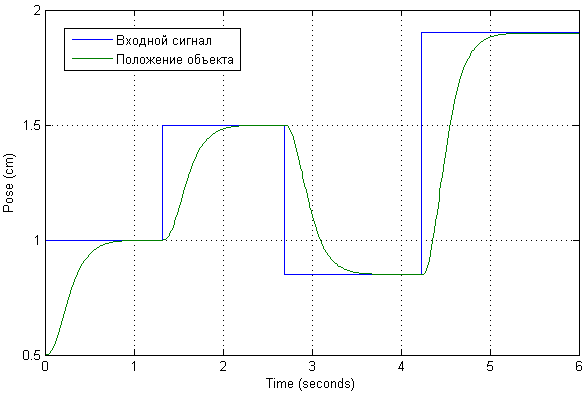
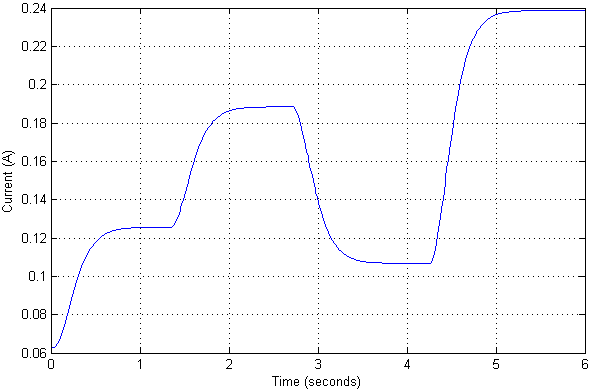
Il s'avère que la valeur actuelle à de telles positions de l'objet n'est pas si significative. Les transitoires eux-mêmes en position sont de nature apériodique, sans dépassement ni erreur statique. En fait, il a été réglé par les pôles souhaités du système ajusté.

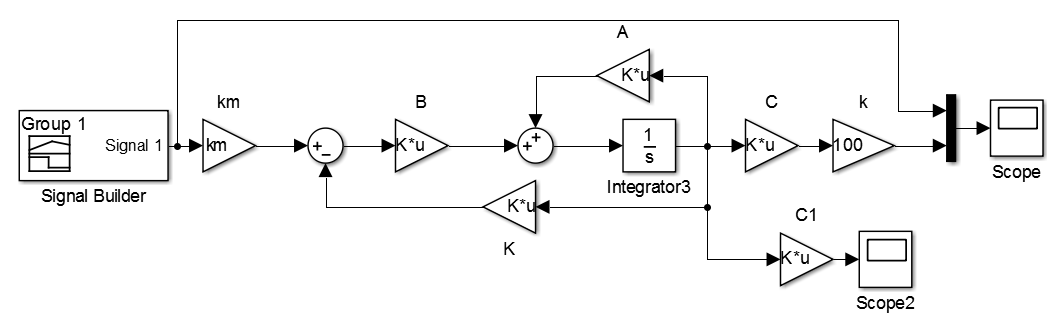
Cependant, cette approximation au point de fonctionnement peut ne pas fonctionner correctement avec le modèle non linéaire d'origine. Regardez ça. Un modèle de système non linéaire avec un contrôleur connecté est illustré ci-dessous.

Ceci est la version finale laissée après toutes les expériences. Des limites ont été fixées sur la tension d'entrée (0-12 V) et la position de l'objet lui-même (0-4 cm). Le deuxième élément du régulateur a été exclu, car avec lui le processus de transition était instable:

Après des modifications du circuit, les transitoires ressemblent maintenant à ceci:

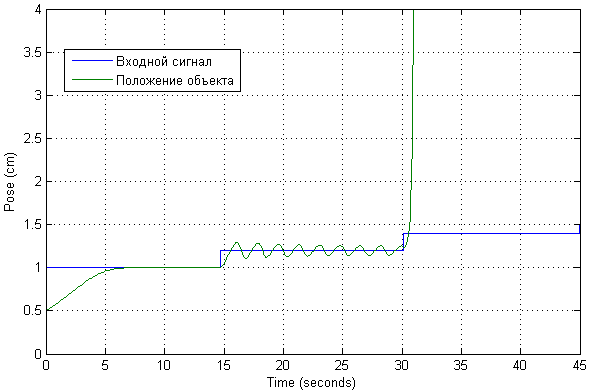
La plage de fonctionnement possible d'un tel système a été immédiatement vérifiée. Vous pouvez voir que la position souhaitée sera atteinte avec de légères déviations par rapport au point de départ. Dans ce cas, une manifestation d'oscillation importante est possible.

Dans ce cas, la valeur actuelle est la suivante:

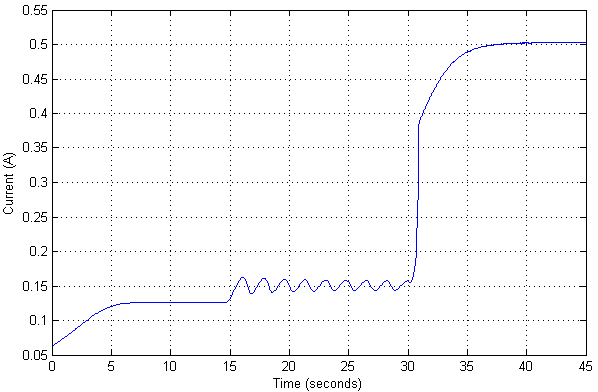
Puisqu'il y a déjà eu une vérification pour un modèle non linéaire d'un objet, vous pouvez également voir quelle peut être la valeur de position maximale d'un objet auquel il ne perd toujours pas sa stabilité.

Après avoir modélisé avec différents signaux d'entrée, il a été constaté que le modèle linéarisé est très bon. Nous allons donc ici démontrer les transitoires en fonction du signal d'entrée initial augmenté de 10 fois.

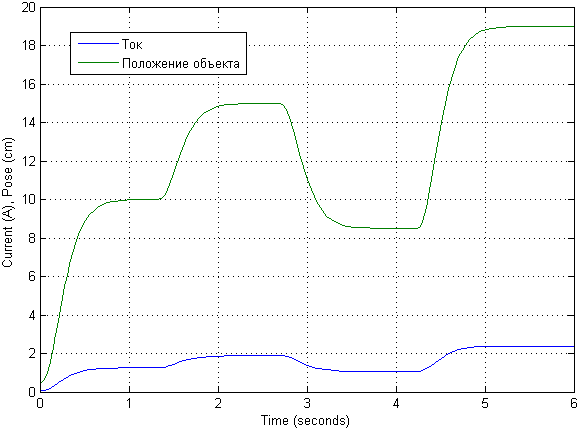
Le modèle mathématique lui-même pourrait sembler un peu différent. Sa description est tirée de la description du modèle mathématique.

Conclusion

Le contrôle modal pour ce modèle non linéaire d'un système de lévitation magnétique n'est pas du tout adapté à des besoins pratiques. D'autres implémentations de ce système de lévitation magnétique doivent être envisagées.

Quant au travail du baccalauréat, l'auteur a mis en place une installation simple sur la lévitation, qui sera décrite séparément à l'avenir.