Quelques mots sur la "section dorée" au sens traditionnel
On pense que si le segment est divisé en parties de telle manière que la plus petite partie se rapporte au plus grand, comme le plus grand - au segment entier, alors une telle division donne une proportion de 1/1618, que les anciens Grecs, l'empruntant à des Égyptiens encore plus anciens, appelés " le nombre d'or. " Et que de nombreuses structures architecturales - le rapport des contours des bâtiments, la relation entre leurs éléments clés - des pyramides égyptiennes aux constructions théoriques de Le Corbusier - étaient basées sur cette proportion.
Elle correspond également aux nombres de Fibonacci, dont la spirale donne une illustration géométrique détaillée de cette proportion.
De plus, la taille du corps humain (de la plante des pieds au nombril, du nombril à la tête, de la tête aux doigts d'une main levée), à partir des proportions idéales vues au Moyen Âge (l'homme de Vitruve, etc.), et se terminant par des mesures anthropométriques de la population de l'URSS, encore proche de cette proportion.
Et si nous ajoutons que de telles figures ont été trouvées dans des objets biologiques complètement différents: coquilles de mollusques, disposition des graines dans un tournesol et des cônes de cèdre, alors il est clair pourquoi un nombre irrationnel commençant par 1 618 a été déclaré "divin" - ses traces sont même tracées sous la forme de galaxies gravitant vers Spirales de Fibonacci!
Compte tenu de tous les exemples ci-dessus, nous pouvons supposer:
- nous traitons vraiment de «big data»,
- même en première approximation, ils pointent vers une certaine, sinon universalité, puis une distribution inhabituellement large de la "section d'or" et des valeurs proches de celle-ci.
En économie
Diagrammes de Lorentz largement connus et largement utilisés pour visualiser les revenus de la population. Ces puissants outils macroéconomiques avec diverses variations et raffinements (coefficient de décile, indice de Gini) sont utilisés dans les statistiques pour la comparaison socio-économique des pays et de leurs caractéristiques et peuvent être une justification pour prendre de grandes décisions politiques et budgétaires dans le domaine de la fiscalité, des soins de santé, des plans de développement des pays en développement et régions.
Et bien que les revenus et les dépenses soient étroitement liés dans la vie quotidienne normale, dans Google, ce n'est pas le cas ... C'est incroyable, mais j'ai réussi à trouver le lien entre les diagrammes de Lorentz et la répartition des dépenses uniquement pour deux auteurs russes (je serais reconnaissant si quelqu'un connaissait de tels travaux comme dans Secteur russe et anglophone d'Internet).
Le premier est une thèse de T. M. Bueva. La thèse a été consacrée, en particulier, à l'optimisation des coûts dans les élevages de volailles Mari.
Un autre auteur, V.V. Matokhin (des liens réciproques des auteurs sont disponibles), aborde la question à plus grande échelle. Matokhin, physicien dans l'enseignement primaire, est engagé dans le traitement statistique des données utilisées dans la prise de décisions managériales, ainsi que dans l'évaluation de l'adaptabilité et de la gérabilité des entreprises.
Le concept et les exemples donnés ci-dessous sont tirés des travaux de V.Matokhin et de ses collègues (Matokhin, 1995), (Antoniou et al., 2002), (Kryanev et al., 1998), (Matokhin et al. 2018). À cet égard, il convient d'ajouter que d'éventuelles erreurs d'interprétation de leurs œuvres sont la propriété exclusive de l'auteur de ces lignes et ne peuvent être imputées aux textes académiques originaux.
Une constance inattendue
Reflété dans les graphiques ci-dessous.
1. Répartition des subventions pour le concours d'ouvrages scientifiques et techniques dans le cadre du programme national «Supraconductivité à haute température». (Matokhin, 1995)
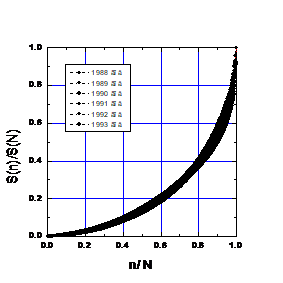Fig.1. Proportions dans l'allocation annuelle de fonds aux projets en 1988-1994.Les principales caractéristiques des distributions annuelles sont présentées dans le tableau 3, où SN est le montant annuel des fonds alloués (en millions de roubles) et N est le nombre de projets financés. Compte tenu du fait que la composition du jury du concours, le budget du concours, et même le montant d'argent (avant la réforme de 1991 et après) ont changé au fil des ans, la stabilité des courbes en temps réel est étonnante. La barre noire sur le graphique est constituée de points expérimentaux.
Tableau 32. La courbe des coûts associés aux ventes de stocks (Kotlyar, 1989)
Fig.23. Barème des taux de salaire Chin
À titre d'exemple, pour construire le diagramme, nous avons pris les données du document «Bulletin: combien de rangs selon les états du salaire annuel ordinaire devraient avoir» (Suvorov, 2014) («La science du gain»).
4. L'horaire de travail moyen du cadre intermédiaire américain (Mintzberg, 1973)
Fig.4Les graphiques normalisés donnés suggèrent qu'il existe une tendance générale dans les activités économiques qu'ils illustrent. Avec une différence radicale dans les spécificités de l'activité économique, en son lieu et en son temps, il est très probable que la similitude des calendriers soit dictée par une condition fondamentale du fonctionnement des systèmes économiques. Au cours de millénaires de conduite d'activité économique, sur la base d'un grand nombre d'essais et d'erreurs, les sujets de cette activité ont cherché à tâtons une stratégie optimale d'allocation des ressources. Et l'utiliser intuitivement dans les activités actuelles. Cette hypothèse est en bon accord avec le principe bien connu de Pareto: 20% de nos efforts donnent 80% des résultats. Quelque chose de similaire est clairement observé ici. Les graphiques donnés expriment une régularité empirique qui, une fois convertie en diagramme de Lorenz, est décrite avec une précision suffisante lorsque l'exposant "alpha" est égal à 2. Dans cet indicateur, le diagramme de Lorentz se transforme en partie de cercle.
Vous pouvez appeler cela, n'ayant pas encore de caractéristique de nom stable, survie. Par analogie avec la survie dans la nature, la survie du système économique est déterminée par son adaptation développée aux conditions de l'environnement socio-économique et sa capacité à s'adapter aux changements des conditions du marché.
Cela signifie qu'un système dans lequel la distribution des dépenses est proche de l'idéal (avec un degré d'alpha égal à 2, ou la distribution des dépenses "autour de la circonférence") a le plus de chances d'être maintenu dans sa forme actuelle. Il est à noter que dans certains cas, une telle répartition détermine la plus grande rentabilité de l'entreprise. Par exemple, ici. Plus le coefficient d'écart par rapport à l'idéal est faible, plus la rentabilité de l'entreprise est élevée (Bueva, 2002).
Tableau (fragment)
Constatations pratiques
Lors de la planification des dépenses d'une entreprise et d'un ménage, il est utile de construire la courbe de Lorentz à partir de celles-ci et de la comparer avec l'idéal. Plus votre graphique est proche de l'idéal, plus il est probable que vous planifiez correctement et que votre activité réussisse. Une telle proximité confirme que vos plans sont proches de l'expérience des activités économiques de l'humanité, déposées dans des lois empiriques universellement reconnues comme le principe de Pareto.
Cependant, nous pouvons supposer que nous parlons ici du fonctionnement d'un système économique mature axé sur la rentabilité. Si nous ne parlons pas de maximiser les bénéfices, mais, par exemple, de la tâche de moderniser l'entreprise ou d'augmenter fondamentalement sa part de marché, votre courbe de répartition des coûts s'écartera du cercle.
Il est clair que dans le cas d'une start-up avec son économie spécifique, le diagramme de Lorentz correspondant à la plus forte probabilité de réussite s'écartera également du cercle. On peut émettre l'hypothèse que les écarts de la courbe de répartition des dépenses au sein du cercle correspondent à la fois à des risques accrus et à une adaptabilité réduite de l'entreprise. Cependant, sans s'appuyer sur de grands tableaux statistiques pour les start-ups (à la fois réussies et infructueuses), des prévisions qualifiées raisonnables ne sont guère possibles.
Selon une autre hypothèse, la déviation de la courbe de répartition des coûts du cercle vers l'extérieur, peut être un signal comme une régulation excessive du contrôle, et un signal de faillite imminente. Pour tester cette hypothèse, une certaine base de référence est également nécessaire qui, comme dans le cas des start-ups, est peu susceptible d'exister dans le domaine public.
Au lieu d'une conclusion
Les premières grandes publications sur ce sujet remontent à 1995 (Matokhin, 1995). Et le peu connu de ces œuvres, avec leur universalité et l'utilisation radicalement nouvelle de modèles et d'outils largement utilisés par les économistes, reste en quelque sorte un mystère ...