Hilbert, Lebesgue ... et le vide

Sous la coupe, la question de savoir comment un bon algorithme d'indexation multidimensionnelle devrait être organisé est étudiée. Étonnamment, il n'y a pas tant d'options.

Indices unidimensionnels, arbres B

La mesure du succès de l'algorithme de recherche sera considérée comme 2 faits -

1. l'établissement du fait de sa présence ou de son absence se produit pour le nombre logarithmique (par rapport à la taille de l'index) de lectures de pages disque
2. le coût d'émission d'un résultat est proportionnel à son volume

En ce sens, les arbres B réussissent assez bien et la raison peut être considérée comme l'utilisation d'un arbre équilibré. La simplicité de l'algorithme est due à la dimension unique de l'espace clé - si nécessaire, divisez la page, il suffit de diviser par deux l'ensemble d'éléments triés de cette page. Généralement divisé par le nombre d'éléments, bien que cela ne soit pas nécessaire.

Parce que les pages de l'arbre sont stockées sur le disque, on peut dire que l'arbre B a la capacité de convertir très efficacement l'espace clé unidimensionnel en espace disque unidimensionnel.

Lorsque vous remplissez un arbre avec plus ou moins de «bonne insertion», et c'est un cas assez courant, les pages sont générées dans l'ordre de croissance des clés, alternant parfois avec des pages plus élevées. Il y a de fortes chances qu'ils soient également sur le disque. Ainsi, sans aucun effort, une localité de données élevée est atteinte - les données dont la valeur est proche seront quelque part à proximité et sur le disque.

Bien sûr, lors de l'insertion de valeurs dans un ordre aléatoire, les clés et les pages sont générées de manière aléatoire, à la suite de quoi le soi-disant fragmentation d'index. Il existe également des outils anti-fragmentation qui restaurent la localisation des données.

Il semblerait qu'à notre époque des disques RAID et SSD, l'ordre de lecture à partir du disque n'a pas d'importance. Mais, au contraire, il n'a pas la même signification qu'auparavant. Il n'y a pas de transfert physique des têtes dans le SSD, donc sa vitesse de lecture aléatoire ne baisse pas des centaines de fois par rapport à une lecture solide, comme un disque dur. Et seulement une fois tous les 10 ou plus .

Rappelons que les B-arbres sont apparus en 1970 à l'ère des bandes magnétiques et des tambours. Lorsque la différence de vitesse d'accès aléatoire pour la bande et le tambour mentionnés était beaucoup plus dramatique qu'en comparaison avec le disque dur et le SSD.

De plus, 10 fois comptent également. Et ces 10 fois incluent non seulement les caractéristiques physiques du SSD, mais aussi le point fondamental - la prévisibilité du comportement du lecteur. Si le lecteur est très susceptible de demander le bloc suivant pour ce bloc, il est logique de le télécharger de manière proactive, par hypothèse. Et si le comportement est chaotique, toutes les tentatives de prédiction sont dénuées de sens et même nuisibles.

Indexation multidimensionnelle

De plus, nous traiterons de l'indice des points à deux dimensions (X, Y), simplement parce qu'il est pratique et intuitif de travailler avec eux. Mais les problèmes sont fondamentalement les mêmes.

Une option simple, «non sophistiquée» avec des indices séparés pour X et Y ne passe pas selon notre critère de succès. Il ne donne pas le coût logarithmique d'obtention du premier point. En fait, pour répondre à la question, y a-t-il quelque chose dans la mesure souhaitée, nous devons

• faire une recherche dans l'index X et obtenir tous les identifiants de l'étendue de l'intervalle X
• similaire pour Y
• croisent ces deux ensembles d'identifiants

Déjà, le premier élément dépend de la taille de l'étendue et ne garantit pas le logarithme.

Pour être «réussi», un index multidimensionnel doit être organisé comme un arbre plus ou moins équilibré. Cette déclaration peut sembler controversée. Mais l'exigence d'une recherche logarithmique nous dicte exactement un tel dispositif. Pourquoi pas deux arbres ou plus? Déjà considérée comme l'option "peu sophistiquée" et inadaptée avec deux arbres. Il y en a peut-être de convenables. Mais deux arbres - c'est deux fois plus de verrous (y compris simultanés), deux fois plus cher, des chances significativement plus grandes d'attraper un blocage. Si vous pouvez vous en sortir avec un seul arbre, vous devez absolument l'utiliser.

Compte tenu de tout cela, le désir de prendre comme base l'expérience très réussie de l'arbre B et de la «généraliser» pour travailler avec des données bidimensionnelles est tout à fait naturel.

L'arbre R est donc apparu.

R-tree

L'arbre R est organisé comme suit:
Au départ, nous avons une page vierge, ajoutez-y simplement des données (points).
Mais ici, la page est pleine et elle doit être divisée.
Dans l'arbre B, les éléments de la page sont classés de manière naturelle, la question est donc de savoir combien couper. Il n'y a pas d'ordre naturel dans l'arbre R. Il y a deux options:

• Mettez de l'ordre, c'est-à-dire introduire une fonction qui, basée sur X&Y, donnera une valeur selon laquelle les éléments de page seront ordonnés et divisés en fonction de cela. Dans ce cas, l'index entier dégénère en un arbre B régulier construit à partir des valeurs de la fonction spécifiée. En plus des avantages évidents, il y a une grande question - bien, bien, nous avons indexé, mais comment regarder? Plus à ce sujet plus tard, considérons d'abord la deuxième option.
• Divisez la page par critères spatiaux. Pour ce faire, chaque page doit être affectée à l'étendue des éléments situés sur / en dessous. C'est-à-dire la page racine a l'étendue de la couche entière. Lors du fractionnement, deux pages (ou plus) sont générées, dont l'étendue est incluse dans l'étendue de la page parent (pour la recherche).

Il y a une pure incertitude. Comment diviser exactement la page? Horizontale ou verticale? Procéder de la moitié de la surface ou de la moitié des éléments? Mais que se passe-t-il si les points forment deux grappes, mais vous ne pouvez les séparer qu'avec une ligne diagonale? Et s'il y a trois clusters?

---

La simple présence de telles questions indique que l'arbre R n'est pas un algorithme. Il s'agit d'un ensemble d'heuristiques, au moins pour fractionner une page lors de l'insertion, pour fusionner des pages lors de la suppression / modification, pour le prétraitement pour l'insertion en bloc.

L'heuristique implique la spécialisation d'un arbre particulier sur un type de données particulier. C'est-à-dire sur des ensembles de données d'un certain type, elle se trompe moins souvent. "L’heuristique ne peut pas être complètement trompée, car dans ce cas, ce serait un algorithme »©.

Que signifie l'erreur heuristique dans ce contexte? Par exemple, que la page sera fractionnée / fusionnée sans succès et que les pages commenceront à se chevaucher partiellement. Si soudainement l'étendue de la recherche tombe sur la zone de chevauchement des pages, le coût de la recherche ne sera déjà pas tout à fait logarithmique. Au fil du temps, lorsque vous insérez / supprimez, le nombre d'erreurs s'accumule et les performances de l'arborescence commencent à se dégrader.


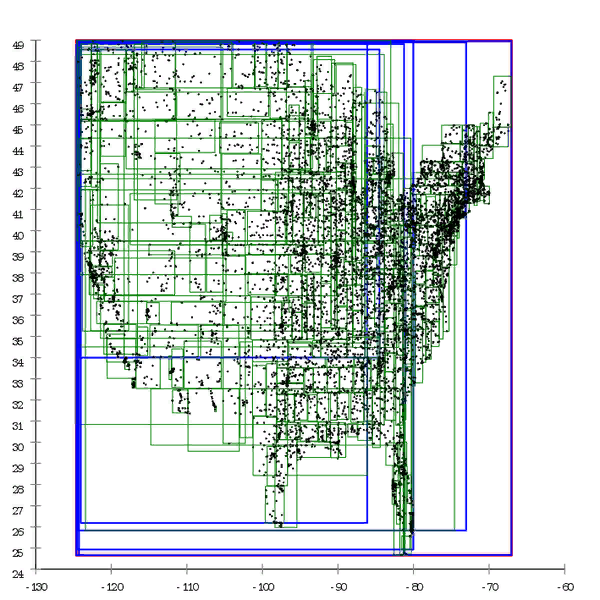Figure 1 Voici un exemple d'arbre R *, qui est construit de manière naturelle.


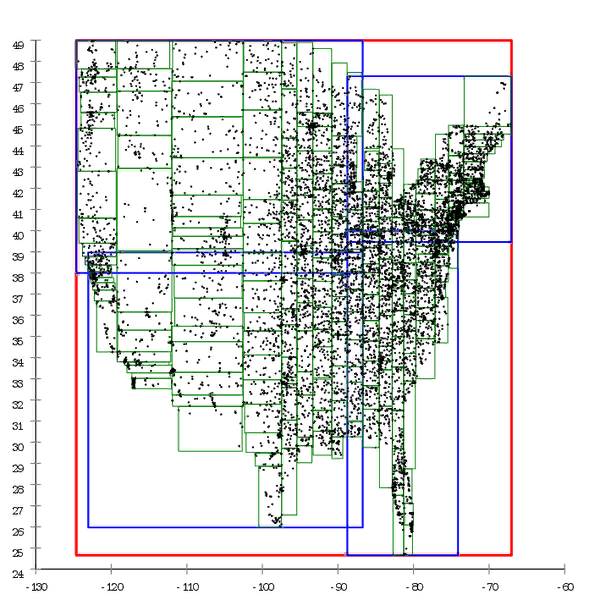Figure 2 Et ici, le même ensemble de données est prétraité et l'arbre est construit par insertion en masse

On peut dire que l'arbre B se dégrade également avec le temps, mais il s'agit d'une dégradation légèrement différente. Les performances de l'arbre B diminuent du fait que ses pages ne sont pas alignées. Ceci est facilement traité en «redressant» l'arbre - défragmentation. Dans le cas d'un arbre R, il n'est pas si facile de s'en débarrasser, la structure de l'arbre lui-même est «courbe» afin de corriger la situation, il doit être complètement reconstruit.

Les généralisations de l'arbre R aux espaces multidimensionnels ne sont pas évidentes. Par exemple, lors du fractionnement des pages, nous avons minimisé le périmètre des pages enfants. Que minimiser dans le cas tridimensionnel? Volume ou surface? Et dans le cas à huit dimensions? Le bon sens n'est plus un conseiller.

L'espace indexé pourrait bien être non isotrope. Pourquoi ne pas indexer non seulement les points, mais leurs positions dans le temps, c'est-à-dire (X, Y, t). Dans ce cas, par exemple, les heuristiques basées sur le périmètre n'ont pas de sens puisque empile la longueur à intervalles de temps.

L'impression générale de l'arbre R est quelque chose comme des crustacés à pieds branchiaux . Ceux-ci ont leur propre niche écologique dans laquelle il est difficile de rivaliser avec eux. Mais dans le cas général, ils n'ont aucune chance de concurrencer les animaux plus développés.

Arbre quad

Dans un quadtree, chaque page non-feuille a exactement quatre descendants, qui divisent également son espace en quadrants.


Figure 3 Exemple d'un arbre quad construit

Ce n'est pas une bonne conception de base de données.

• Chaque page ne réduit l'espace de recherche pour chaque coordonnée que deux fois. Oui, cela fournit la complexité logarithmique de la recherche, mais c'est le logarithme de base 2, pas le nombre d'éléments sur la page, (même 100) comme dans un arbre B.
• Chaque page est petite, mais derrière elle, vous devez toujours aller sur le disque.
• La profondeur de l'arbre quad doit être limitée, sinon son déséquilibre affecte les performances. Par conséquent, sur des données fortement regroupées (par exemple, des maisons sur une carte - il y a beaucoup de villes dans les villes, peu dans les champs), une grande quantité de données peut s'accumuler sur les pages de feuilles. Un index à partir d'un index exact devient bloc et nécessite un post-traitement.
  
  Une taille de réseau mal sélectionnée (profondeur d'arbre) peut nuire aux performances. Néanmoins, je voudrais que les performances de l'algorithme ne dépendent pas de manière critique du facteur humain.
  
• Le coût de l'espace pour stocker un point est assez élevé.

Numérotation des espaces

Il reste à considérer la version précédemment différée avec une fonction qui, sur la base d'une clé multidimensionnelle, calcule la valeur d'écriture dans un arbre B régulier.

La construction d'un tel index est évidente, et l'index lui-même a tous les avantages de l'arbre B. La seule question est de savoir si cet index peut être utilisé pour une recherche efficace.

Il existe un grand nombre de ces fonctions, on peut supposer que parmi elles il y a un petit nombre de «bonnes», un grand nombre de «mauvaises» et un grand nombre de «tout simplement horribles».

Trouver une fonction terrible n'est pas difficile - nous sérialisons la clé dans une chaîne, considérons MD5 à partir de celle-ci et obtenons une valeur complètement inutile pour nos besoins.

Et comment aborder le bien? Il a déjà été dit qu'un index utile fournit la «localité» des données - des points qui sont proches dans l'espace et sont souvent proches les uns des autres lorsqu'ils sont enregistrés sur le disque. Appliquée à la fonction souhaitée, cela signifie que pour des points spatialement proches, elle donne des valeurs proches.

Une fois dans l'index, les valeurs calculées apparaîtront sur les pages "physiques" dans l'ordre de leurs valeurs. Du point de vue du «sens physique», l'étendue de la recherche devrait affecter le moins de pages d'index physique possible. Ce qui est généralement évident. De ce point de vue, les courbes de numérotation qui «tirent» les données sont «mauvaises». Et ceux qui «se confondent en boule» - plus près du «bien».

Numérotation naïve

Une tentative de presser un segment dans un carré (hypercube) tout en restant dans la logique de l'espace unidimensionnel, c'est-à-dire couper en morceaux et remplir le carré avec ces morceaux. Ça pourrait être


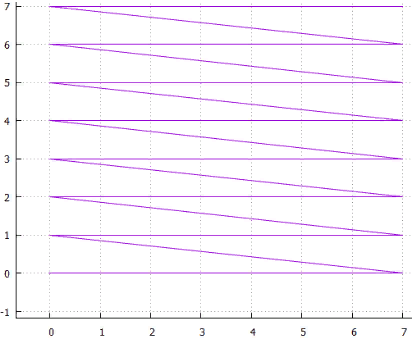Balayage 4 lignes


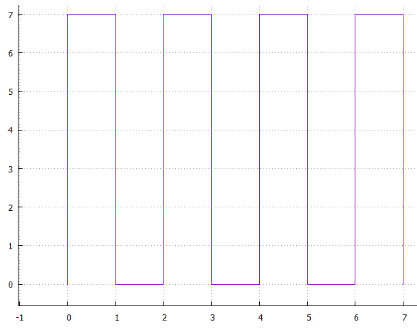5 entrelacé


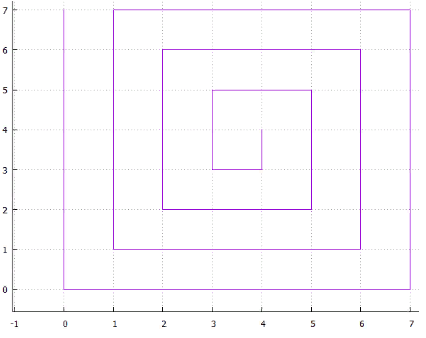Fig.6 spirale

ou ... vous pouvez trouver beaucoup d'options, elles ont toutes deux inconvénients

1. ambiguïté, par exemple: pourquoi la spirale est enroulée dans le sens horaire et non contre elle, ou pourquoi le balayage horizontal est d'abord le long de X puis le long de Y
   
2. la présence de longues pièces droites qui rendent l'utilisation d'une telle méthode inefficace pour l'indexation multidimensionnelle (périmètre de grande page)

Fonctionnalités d'accès direct

Si la principale revendication des méthodes «naïves» est qu'elles génèrent des pages très allongées, générons nous-mêmes les pages «correctes».

L'idée est simple - qu'il y ait une division externe de l'espace en blocs, attribuez un identifiant à chaque bloc et ce sera la clé de l'index spatial.

• laissez les coordonnées X et Y sur 16 bits (pour plus de clarté)
• nous allons couvrir l'espace avec des blocs carrés de taille 1024X1024
• grossir les coordonnées, décaler de 10 bits vers la droite
• et obtenez l'ID de la page, collez les bits de X&Y. Maintenant, dans l'identifiant, les 6 chiffres inférieurs sont les plus anciens de X, les 6 chiffres suivants sont les plus anciens de Y
  

Il est facile de voir que les blocs forment un balayage de ligne, par conséquent, pour trouver des données pour l'étendue de recherche, vous devrez effectuer une recherche / lecture dans l'index pour chaque ligne de blocs sur laquelle cette étendue est appliquée. En général, cette méthode fonctionne très bien, bien qu'elle présente plusieurs inconvénients.

• lors de la création d'un index, vous devez choisir la taille de bloc optimale, ce qui n'est pas évident
• si le bloc est significativement plus grand qu'une requête classique, la recherche sera inefficace car doivent trop lire et filtrer (post-traitement)
  
• si le bloc est significativement plus petit qu'une requête typique, la recherche sera inefficace car devra faire beaucoup de requêtes ligne par ligne
  
• si le bloc contient en moyenne trop ou trop peu de données, la recherche sera inefficace
  
• si les données sont regroupées (ex: à la maison sur la carte), la recherche ne sera pas efficace partout
• si l'ensemble de données a augmenté, il se peut bien que la taille du bloc cesse d'être optimale.
  

En partie, ces problèmes sont résolus en créant des blocs à plusieurs niveaux. Pour le même exemple:

• veulent toujours des blocs 1024X1024
• mais maintenant, nous aurons toujours des blocs de niveau supérieur de blocs inférieurs de taille 8X8
• la clé est disposée comme suit (de bas en haut):
  3 chiffres - chiffres 10 ... 12 coordonnées X
  3 chiffres - chiffres 10 ... 12 coordonnées Y
  3 chiffres - chiffres 13 ... 15 coordonnées X
  3 chiffres - chiffres 13 ... 15 coordonnées Y

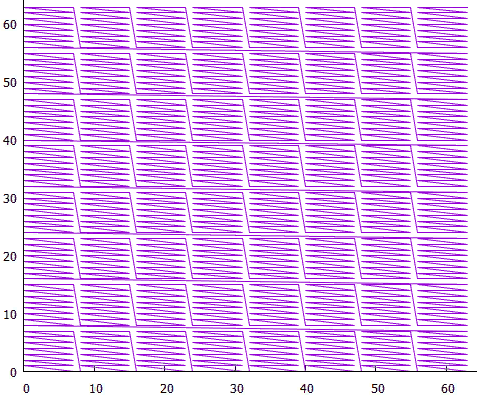7 blocs de bas niveau forment des blocs de haut niveau

Maintenant, pour les grandes étendues, vous n'avez pas besoin de lire un grand nombre de petits blocs, cela se fait au détriment des blocs de haut niveau.

Fait intéressant, il était possible de ne pas rendre les coordonnées plus rugueuses, mais de la même manière de les presser dans la clé. Dans ce cas, le post-filtrage serait moins cher car se produirait lors de la lecture de l'index.

Les index GRID spatiaux sont organisés dans MS SQL de la même manière; jusqu'à 4 niveaux de bloc y sont autorisés.


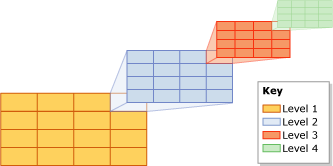Fig.8 Index GRID

Une autre façon intéressante d'indexation directe consiste à utiliser un arbre quadruple pour le partitionnement externe de l'espace.

L'arbre quad est utile en ce qu'il peut s'adapter à la densité des objets, car lorsque le nœud déborde, il se divise. Par conséquent, lorsque la densité des objets est élevée, les blocs se révèlent petits et vice versa. Cela réduit le nombre d'appels d'index vides.

Certes, l'arbre quad est une construction peu pratique pour la reconstruction à la volée, il est avantageux de le faire de temps en temps.

De la chose agréable, lors de la reconstruction d'un arbre quadruple, il n'est pas nécessaire de reconstruire l'index si les blocs sont identifiés par le code Morton et les objets sont encodés à l'aide de celui-ci. Voici l'astuce: si les coordonnées du point sont encodées avec un code Morton, l'identifiant de page est un préfixe dans ce code. Lors de la recherche de données de page, toutes les clés comprises entre [préfixe] 00 ... 00B et [préfixe] 11 ... 11B sont sélectionnées, si la page est divisée, cela signifie que seul le préfixe de ses descendants s'est allongé.

Fonctionnalités similaires

La première chose qui me vient à l'esprit lorsque l'on mentionne des fonctions auto-similaires est le «balayage des courbes». "Une courbe notable est une cartographie continue, dont le domaine est le segment unitaire [0, 1], et le domaine est l'espace euclidien (plus strictement, topologique)." Un exemple est la courbe de Peano.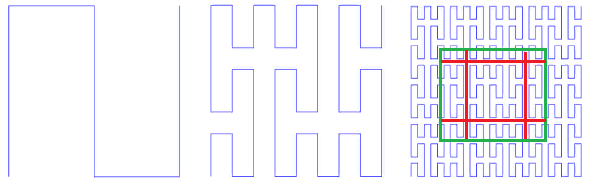


Fig.9 premières itérations de la courbe de Peano

Dans le coin inférieur gauche se trouve le début de la zone de définition (et la valeur zéro de la fonction), dans le coin supérieur droit la fin (et 1), chaque fois que nous déplaçons 1 étape, ajoutez 1 / (N * N) à la valeur (à condition que N - degré 3, bien sûr). Par conséquent, dans le coin supérieur droit, la valeur atteint 1. Si nous en ajoutons un à chaque étape, une telle fonction numérote simplement le réseau carré de manière séquentielle, ce que nous voulions.

Toutes les courbes de balayage sont auto-similaires. Dans ce cas, le simplexe est un carré de 3 x 3. À chaque itération, chaque point du simplexe se transforme en le même simplexe, pour assurer la continuité, il faut recourir à des mappings (flips).

L'autosimilarité est une qualité très importante pour nous. Cela donne de l'espoir pour la valeur logarithmique de la recherche. Par exemple, pour un simplexe 3x3, tous les nombres générés dans chacun des 9 carrés élémentaires par des itérations de détail ultérieures seront dans la même plage. Tout simplement parce que le nombre est le chemin parcouru depuis le début. C'est-à-dire si vous divisez l'étendue en 9 parties, le contenu de chacune d'elles peut être obtenu par une traversée d'index. Et ainsi de suite récursivement, chacun des 9 sous-carrés de chacun des carrés peut être obtenu par une seule requête sur l'index (bien que dans une plage plus petite). L'étendue de la recherche peut donc être décomposée en un petit nombre de sous-requêtes carrées, lues soit en totalité, soit avec un filtrage (autour du périmètre). La figure 9 montre l'étendue de la recherche en vert, divisée par des lignes rouges en sous-requêtes.

Cependant, l'autosimilarité ne rend pas automatiquement la courbe de numérotation appropriée à des fins d'indexation.

• la courbe doit remplir la grille carrée. Nous indexons les valeurs dans les nœuds du réseau carré et chaque fois nous ne voulons pas rechercher un nœud approprié sur le réseau, par exemple triangulaire. Au moins pour éviter les problèmes d'arrondi. Ici, par exemple, tels (figure 10)
  
  
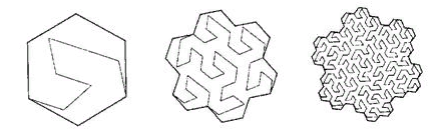
  Figure 10 lac ternaire Kokha
  
  la courbe ne nous convient pas. Bien qu'il «ponte» parfaitement la surface.
  
• la courbe doit remplir l'espace sans lacunes ( dimension fractale D = 2). La voici (Fig.11):
  
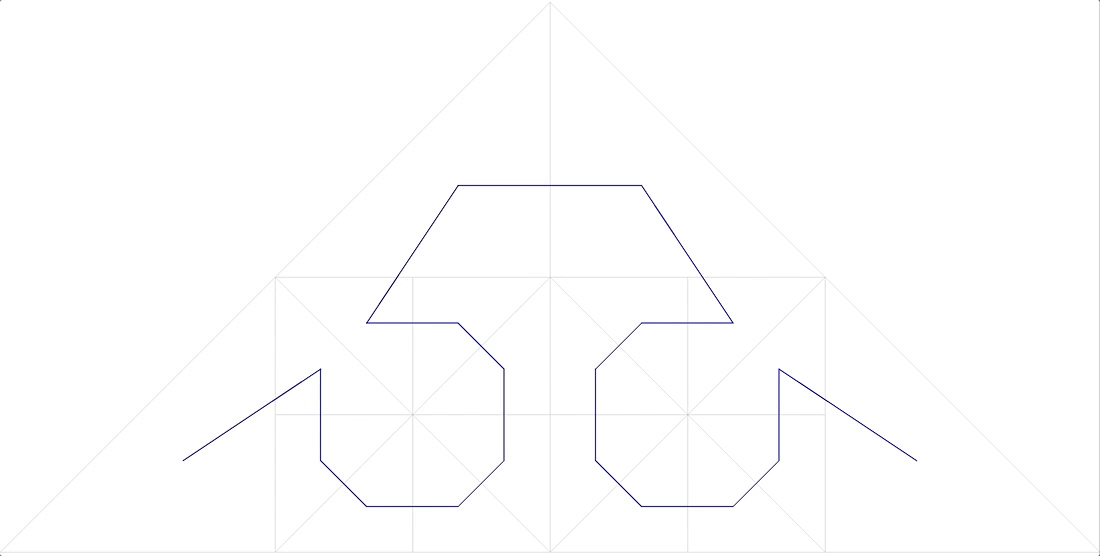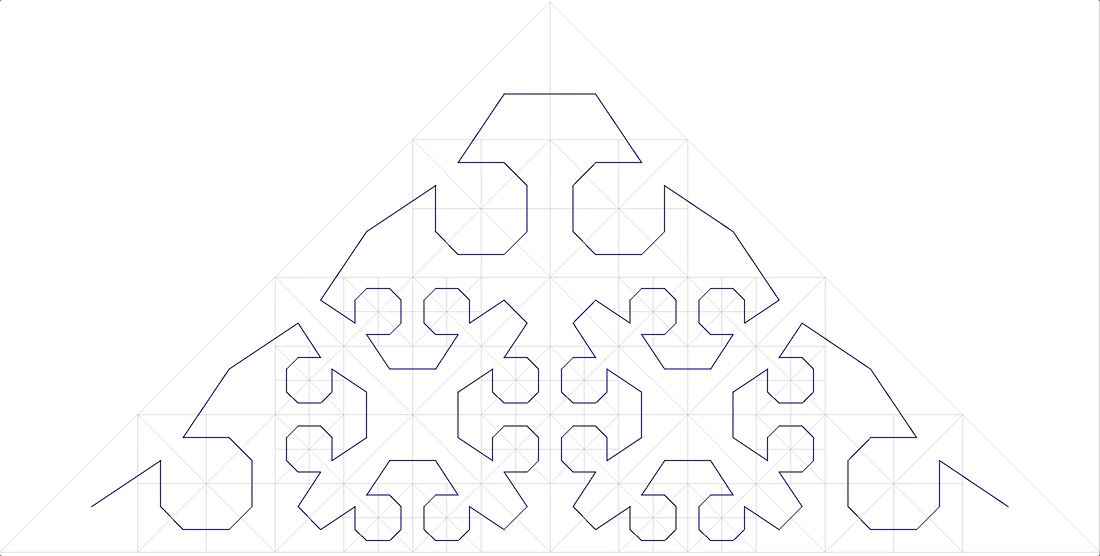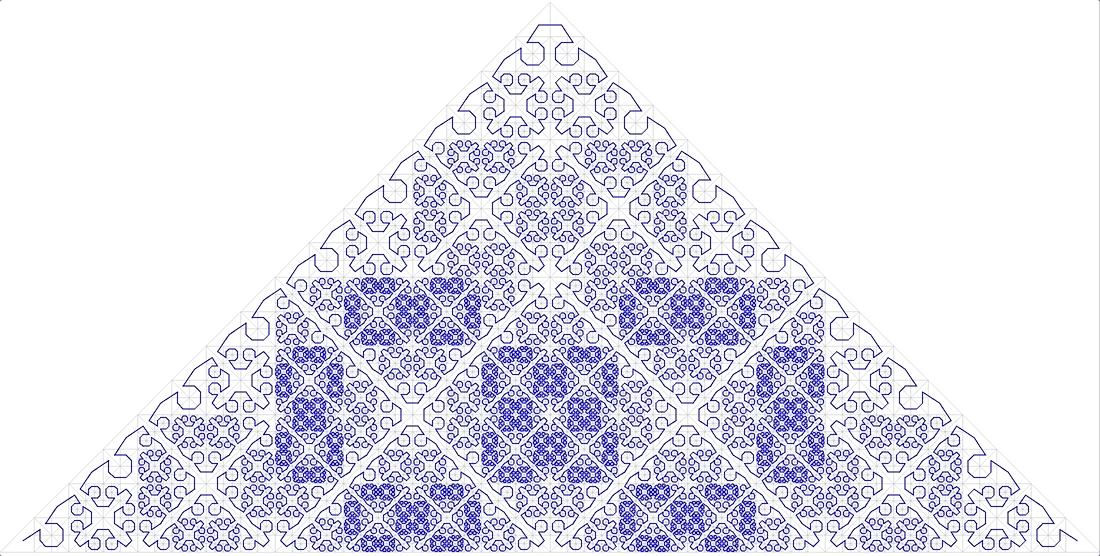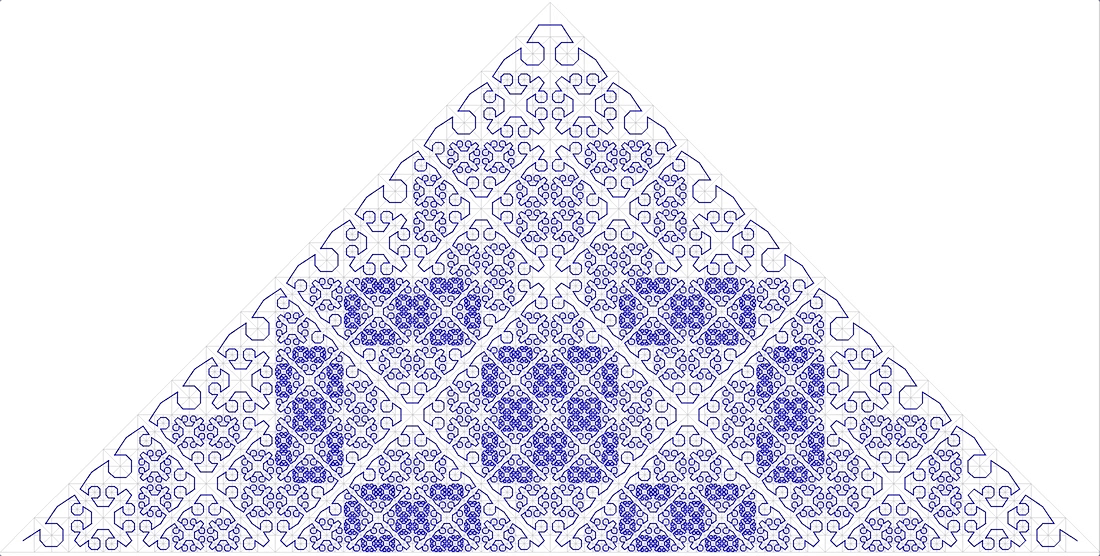
  11 courbe fractale anonyme
  
  ne convient pas non plus.
  
• la valeur de la fonction de numérotation (le chemin parcouru le long de la courbe depuis le début) doit être facilement calculée. Il en résulte qu'en raison de l'ambiguïté qui en résulte, les courbes auto-touchantes ne conviennent pas, comme la courbe de Sierpinski
  
  
  Fig.12 Courbe de Sierpinski
  
  ou, qui est la même chose (pour nous), "en passant le triangle le long de Cesaro "
  
  
  FIG. 13 Triangle Cesaro, pour plus de clarté, l'angle droit est remplacé par 85 °
• il ne doit pas y avoir de paramètres dans la fonction de numérotation, la courbe doit être uniforme (précise à la symétrie). . : ( )
  
  
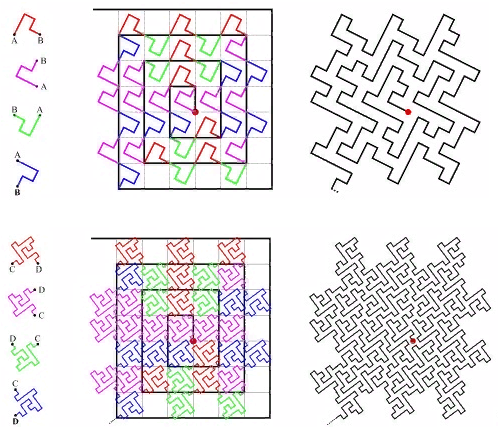
  . 14 “A Plane Filling Curve for the Year 2017”
  
  , ( ) .
  , , , .

— . , . , N- N (N-1) . , , -.


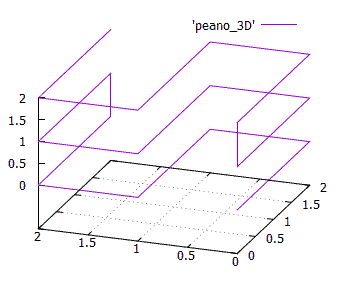. 15 3x3x3

, .

.

, . , ( ). , , . , .

.

• ,
  
• ( ) , . , . — . .
• — , .. .
  
• , . , , . , , — () 3...10% () Z-.
  
  — , .

, () , ( ) .

, , - , . , , . , . .

, ? .

().

, , . , . , 3X3 3 X, 3 Y. . () 5X5, 5 . (ex: 2+3), .

- — , 5- 7- , . . , .

. 2 . 4 . .

, 33 22 , 3 > 2, 44 33, 88 55. , 22…

? . Parce que , . 3X3 , 3 . 8x8 (.16), — 64 .


. 16 8x8

, , 2x2, , .


. 17 2x2

, , , “Z”, “” “”.
, “” , . 4 . 256 8- .

, ( “”), . .


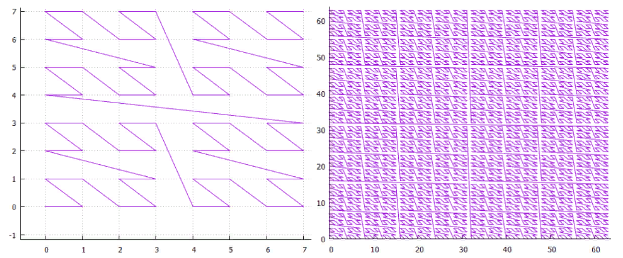. 18 Z-


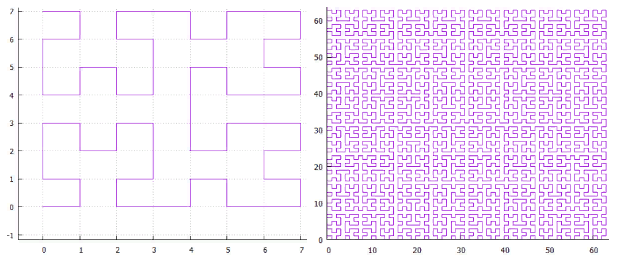. 19 “” —

, . .

• , , .
  —
  
  • (KMin, KMax)
    
  • ( ) KMin, KMax
    
  • , SMin, , SMax
    
  • . , , SMin, . .
  • , , ( ).
    
  • Z- . z- — , — ( ). , , .
• • , , . ,
  • , . — “ ” >= “ ” () , “ ”
    
    
    • “ ” > , ,
      
    • , ,
      
    • “ ” > , , ,
    • “ ” == ,
      
  • • 0 1 —
    • 0 1 —
    • , , 1, 0. .
  
  

Sur une courbe en Z, cela fonctionne comme ceci:


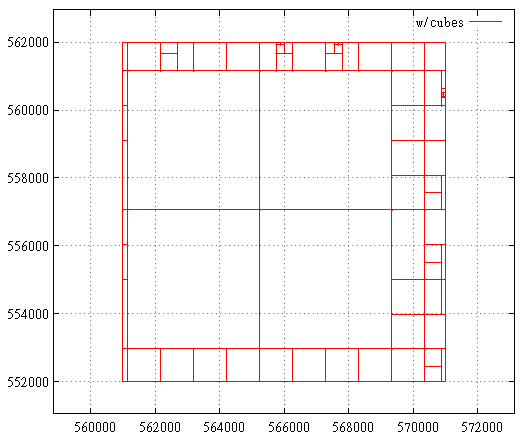FIG. 20 - fractionnement de sous-requête en cas de courbe en Z


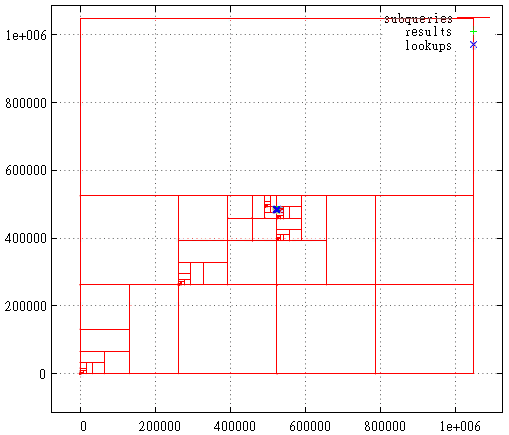FIG. 21 Courbe de Hilbert, le cas où l'étendue de départ est le maximum

La première étape est illustrée ici - couper la couche excédentaire de l'étendue maximale.


FIG. 22 Courbe de Hilbert, zone de requête de recherche

Et voici une ventilation en sous-requêtes, points trouvés et appels d'index dans la zone de requête de recherche. Il s'agit toujours d'une demande très infructueuse du point de vue de la courbe de Hilbert. Habituellement, tout est beaucoup moins sanglant.

Cependant, les statistiques de requête indiquent que (à peu près) sur les mêmes données, un index bidimensionnel basé sur une courbe de Hilbert lit en moyenne 5% de pages de disque en moins, mais il fonctionne à moitié plus lentement. Le ralentissement est également dû au fait que le calcul lui-même (direct et inverse) de cette courbe est beaucoup plus difficile - 2000 horloges de processeur pour Hilbert contre 50 pour la courbe Z.

En cessant de supporter la courbe de Hilbert, l'algorithme pourrait être simplifié; à première vue, un tel ralentissement n'est pas justifié. D'un autre côté, ce n'est qu'un cas à deux dimensions, par exemple, dans un espace à 8 dimensions ou plus, les statistiques peuvent briller avec des couleurs complètement nouvelles. Cette question attend toujours des éclaircissements.

PS : La courbe en Z est parfois appelée courbe d'entrelacement de bits en raison de l'algorithme de calcul de la valeur - les chiffres de chaque coordonnée tombent dans la valeur clé à travers une, ce qui est très technologique. Mais vous pouvez, après tout, entrelacer les décharges non pas individuellement, mais en paquets de 2,3 ... 8 ... pièces. Maintenant, si nous prenons 8 bits, alors sur une clé 32 bits, nous obtenons un analogue de l'index GRID à 4 niveaux de MS SQL. Et dans un cas extrême - un pack de 32 bits chacun - un algorithme de balayage horizontal.

Un tel indice (pas en minuscules, bien sûr) peut être très efficace, encore plus efficace que la courbe Z sur certains ensembles de données. Malheureusement, en raison de la perte de généralité.

PPS : L'index décrit est très similaire au travail avec un arbre quadruple. L'étendue maximale est la page racine de l'arbre quadruple, elle a 4 descendants ... Et donc, l'algorithme peut être attribué à des "méthodes d'accès direct".

Les différences sont toujours fondamentales.

L'arbre quadruple n'est stocké nulle part, il est virtuel, intégré dans la nature même des nombres. Il n'y a aucune restriction sur la profondeur de l'arbre; nous obtenons des informations sur la population de descendants à partir de la population de l'arbre principal. De plus, l'arbre principal est lu une fois, on passe des valeurs les plus petites aux plus anciennes. C'est drôle, mais la structure physique de l'arbre B permet d'éviter les requêtes vides et de limiter la profondeur de récursivité.

Une dernière chose - à chaque itération, seuls deux descendants apparaissent - à partir de là, 4 sous-requêtes peuvent être générées et ne peuvent pas être générées s'il n'y a pas de données sous elles. Dans le cas en 3 dimensions, nous parlerions de 8 descendants, dans le cas en 8 dimensions - environ 256.

PPPS : au début de cet article, nous avons parlé de dichotomie lors de la recherche dans un index multidimensionnel - afin d'obtenir la valeur logarithmique, il est nécessaire de diviser une ressource finie à chaque itération - soit l'espace de valeur clé ou l'espace de recherche. Dans l'algorithme présenté, cette dichotomie s'est effondrée - nous partageons simultanément la clé et l'espace.

«Je vis dans les deux cours et mes arbres sont toujours plus grands.» ( C )

PPPPS : Dès qu'ils appellent la courbe Z, vous avez ici l'ordre Z et l'entrelacement des bits et le code / courbe de Morton. Il est également connu sous le nom de courbe de Lebesgue, afin de maintenir l'équilibre, l'auteur a intitulé l'article, y compris en l'honneur de Henry Leon Lebesgue .

PPPPPS : Dans l'illustration du titre, la vue sur le glacier Fedchenko est tout simplement magnifique et il y a suffisamment de vide. En fait, l'auteur a été impressionné par la façon dont les différentes idées et méthodes s'enchaînent sans heurts, fusionnant progressivement en un seul algorithme. Tout comme les nombreuses petites sources d'eau qui composent le bassin versant forment un seul ruissellement.