Les surfaces aléatoires cachent un ordre complexe

Les mathématiciens ont prouvé qu'un processus aléatoire appliqué à une surface aléatoire génère invariablement certains modèles

Dans l' article d'origine, il s'agit d'une image en trois dimensions qui peut être tordue

Dans le film sur la recherche de l'arche perdue, Indiana Jones a dû chercher une pièce secrète cachant l' arche légendaire de l'Alliance . Pour déterminer son emplacement exact, l'Indiana avait besoin de trouver une carte spéciale, visible uniquement lorsque le soleil brille à travers un cristal spécial dans une certaine pièce à une certaine heure de la journée.

Une idée similaire - que les informations les plus importantes ne peuvent être divulguées qu'avec la coïncidence exacte de certaines circonstances - se retrouve dans de nombreux mythes. Cela se produit en mathématiques, parfois dans des situations inattendues. Maintenant, trois mathématiciens ont prouvé que si un certain type de hasard est réglé très précisément, des figures géométriques complexes apparaissent - comme une carte avec un trésor sur un sol ordinaire.

Ces pièces sont comme des cellules d'échecs dispersées sur des grilles, qui sont elles-mêmes créées par un processus aléatoire. On pourrait penser qu'en empilant le hasard dans le hasard, nous obtenons de la confusion. Il s'avère que, comme dans le cas des flocons de neige, lorsque chacun d'eux est unique, mais en même temps ce sont tous des flocons de neige, le désordre converge vers une forme universelle - si seulement les conditions s'avèrent être exactement comme nécessaires.

Point tournant

Tout le monde sait que les mathématiciens étudient les formulaires. La plupart de ces formes suivent des règles déterministes: si je vous donne des instructions pour construire une sphère, vous recevrez la même sphère à chaque fois.

Mais même les mathématiciens étudient les formes obtenues à la suite de processus aléatoires, tels que, par exemple, la marche aléatoire - un chemin, dont la direction de chaque étape est choisie au hasard. En plus des promenades aléatoires, il existe d'autres types d'objets géométriques aléatoires, par exemple, des surfaces bidimensionnelles aléatoires (imaginez un paysage où les collines et les vallées sont dispersées de manière aléatoire) et des cartes aléatoires (un ensemble de points aléatoires reliés par des lignes).


Surface aléatoire obtenue par collage de triangles

Toutes ces formes sont différentes les unes des autres. Cependant, les mathématiciens ont découvert que ces processus aléatoires convergent vers certaines formes canoniques. Par exemple, toutes les marches aléatoires sont une forme de mouvement brownien avec une marche assez longue. Ces dernières années, les mathématiciens ont découvert des formes canoniques et d'autres processus aléatoires - et ont reçu les plus hautes récompenses pour cela dans leurs domaines.

Les nouvelles preuves sont liées à une compréhension des propriétés sous-jacentes d'un autre processus aléatoire.

Il commence par créer une surface aléatoire. Vous devez d'abord coller les triangles ensemble. Ensuite, ils doivent être appariés de quelque manière que ce soit, uniquement pour que le formulaire résultant soit fermé, comme un paquet sur un cadeau (sans trous). Si vous commencez avec un certain nombre de triangles sur les mains, vous aurez de nombreuses opportunités. Certaines de ces «triangulations» produiront des surfaces presque lisses qui ressemblent à une balle. La plupart d'entre eux auront l'air plus rugueux - comme des surfaces extrêmes ressemblant à des chaînes de montagnes.

"Cela ne ressemblera pas à une sphère régulière, il aura de si grandes pointes", a déclaré Olivier Bernardi , mathématicien de l'Université de Brandeis, co-auteur du travail, qui a également impliqué Nicholas Curien de l'Université de Paris-Sud XI et Gregory Mjermont de la Higher Normal School in Lyon.


Olivier Bernardi, Nicholas Curien et Gregory Myermont

Myermont et un autre mathématicien, Jean-François le Gall , ont établi de nombreuses propriétés de ces triangulations aléatoires dans leurs travaux précédents. La nouvelle preuve va encore plus loin en ajoutant une deuxième couche d'aléatoire en plus de la triangulation aléatoire.

Pour ajouter un nouveau caractère aléatoire, marquez chaque point auquel les triangles se rencontrent aux coins - ce que les mathématiciens appellent un sommet. Colorez les sommets au hasard en noir ou blanc. Vous pouvez le faire en lançant une pièce, bien que la pièce ne soit pas complètement honnête et l'emporte sur un côté.

Après avoir peint les pics, vous pouvez poser diverses questions sur le motif que vous avez créé. L'un des plus basiques: jusqu'où pouvez-vous aller le long de la surface en utilisant un seul sommet noir? Le processus de déplacement le long de sommets connectés de la même couleur est appelé infiltration. Il s'agit d'une façon mathématique d'étudier un phénomène physique du même nom lorsqu'un fluide traverse un milieu poreux.

Il sera facile de s'infiltrer (ou non), selon la répartition du poids de la pièce: si la pièce a tendance à dégager des sommets noirs, l'infiltration est presque garantie; si pour l'extradition des blancs, l'infiltration sera presque certainement impossible.



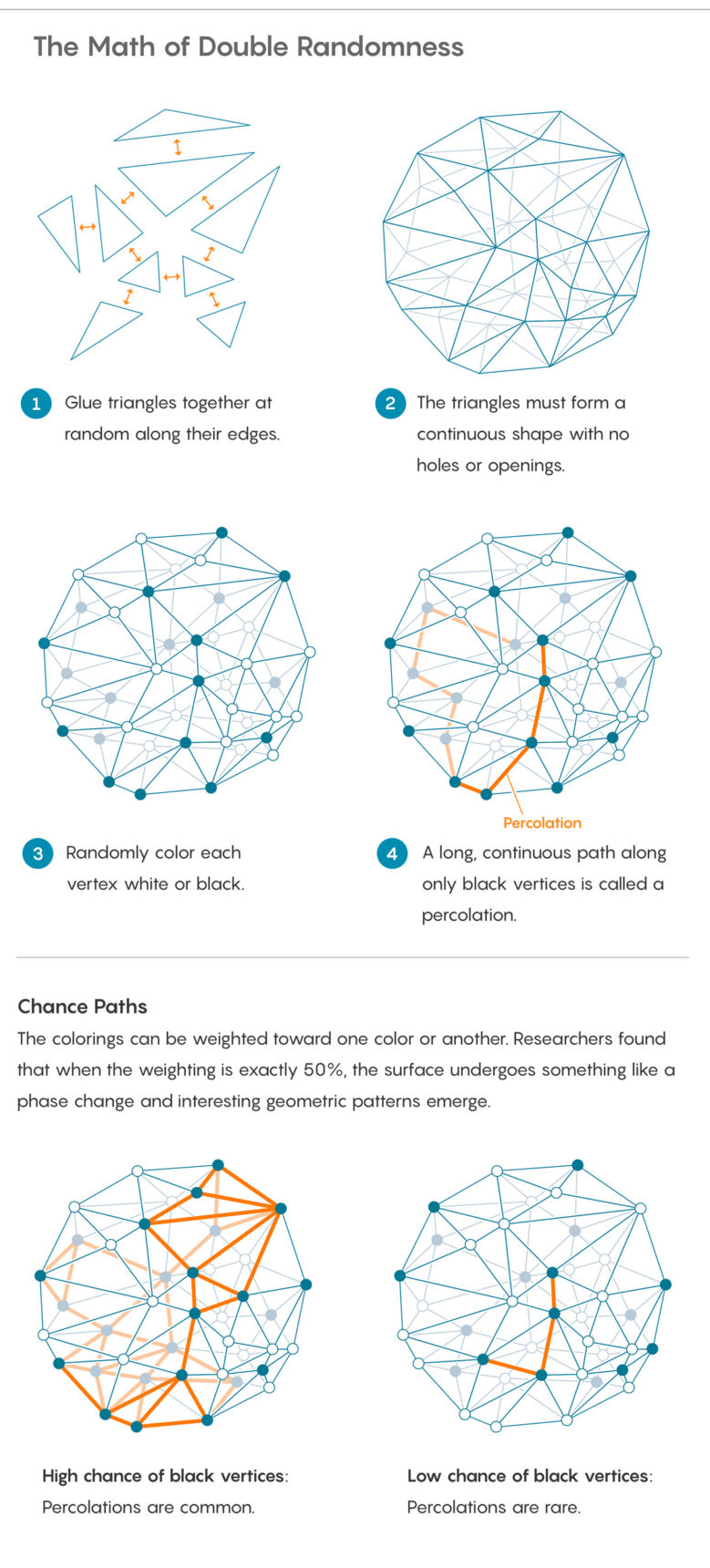
Bernardi, Curien et Myermont étudient des cas se situant entre ces extrêmes - un tournant dans le changement du poids de la pièce, lorsque la fuite passe d'un phénomène presque impossible à presque garanti. Ils appellent ce point un «seuil critique». Ceci est un exemple de transition de phase, ce moment magique où l'eau chaude devient soudainement de la vapeur.

«Le seuil critique signifie que si je modifie légèrement mes paramètres, le comportement de mon système passera de dramatique à dramatique avec un signe différent», a déclaré Curien.

Les physiciens sont intéressés par les transitions de phase parce que bon nombre des phénomènes naturels les plus importants se produisent juste à la veille. Les mathématiciens s'intéressent également aux transitions de phase, car d'importantes propriétés mathématiques apparaissent souvent juste à ces points.

"Nous savons que l'eau bout à 100 degrés, créant tous ces motifs fous et des formes de vapeur", a déclaré Scott Sheffield , mathématicien au MIT. «Parfois, un tel comportement fou et sauvage devient très intéressant. Cette transition de phase nous appelle à la comprendre. »

Dans le nouveau travail, trois mathématiciens prouvent qu'un tel comportement insensé se manifeste précisément dans la transition de phase de la fuite. Ils montrent qu'à ce seuil critique apparaît une forme géométrique - unique et en même temps universelle.

Ordre caché au hasard

La première partie du travail détermine comment corriger une pièce pour que la coloration des sommets tombe sur le seuil entre la présence et l'absence d'infiltration. Confirmant l'intuition, ils prouvent que la pièce idéale est la valeur critique - donnant 50% de chances de tomber noir et 50% de tomber blanc.

«C'est la première partie du travail. Nous prouvons qu'il se passe exactement la moitié d'un événement intéressant », a déclaré Bernardi.


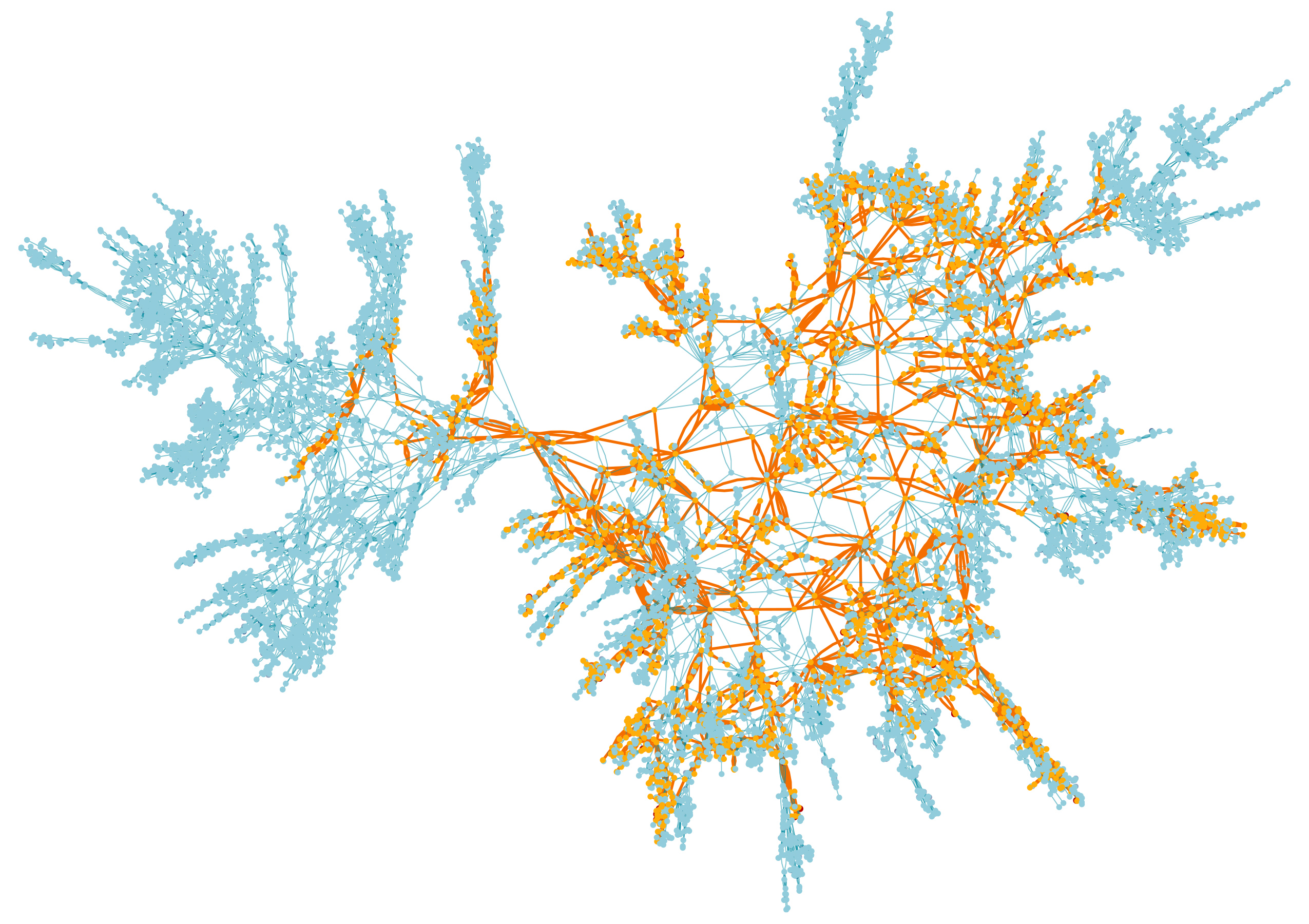Carte des pics d'une surface aléatoire, le plus grand groupe est marqué en orange

Dans la deuxième partie, nous étudions ce qui se passe là-bas. En coloriant les sommets en noir et blanc avec une pièce de monnaie équitable, vous obtenez un bon équilibre entre les grappes de sommets noir et blanc. Les grappes se développent les unes autour des autres, comme des fourrés de mauvaises herbes qui se disputent une place dans un jardin envahi, créant des formes géométriques complexes qui n'apparaissent pas lorsque l'une des fleurs domine parmi les sommets.

"En choisissant un paramètre critique, vous découvrez de grands clusters", a déclaré Sheffield. "Cependant, ils ne tachent pas le tout et ils ne sont pas petits."

Étant donné que la surface a été créée de manière aléatoire et que le processus de coloration des sommets est également aléatoire, le grand cluster sur une surface sera toujours différent du grand cluster sur l'autre. Mais les mathématiciens ont prouvé que pour toutes les surfaces et toutes les façons possibles de colorer leurs sommets, les plus grands groupes auront les mêmes propriétés. La première chose qu'ils ont prouvée est la distribution de probabilité exacte des tailles des plus grands amas noirs sur toutes les surfaces. Ils ont constaté que le plus souvent un groupe d'une certaine taille intermédiaire se produit et que la fréquence d'apparition de groupes plus ou moins grands augmente de façon exponentielle avec la distance de cet intermédiaire.

Ils soutiennent également que tous les grands groupes peuvent être réduits à la même forme canonique, connue sous le nom de «carte stable». La carte stable fait référence à ces grappes de la même manière que le mouvement brownien de marche aléatoire. Cela signifie que si les grappes individuelles sont légèrement éloignées - de sorte que chaque étape aléatoire à l'intérieur de la grappe est moins perceptible dans la géométrie de la figure entière dans son ensemble - alors les grappes prendront progressivement une forme commune. Ils ressemblent à des flocons de neige: ils semblent uniques à proximité, mais leur point commun est clairement visible de loin.

"Ils ont trouvé cette carte stable, la limite naturelle de la mise à l'échelle", a déclaré Sheffield.

Le travail repousse les limites des connaissances concernant les formes et les processus aléatoires accumulés par les mathématiciens ces dernières années. Elle nous révèle aussi que c'est précisément à ce moment où le système aléatoire semble le plus chaotique qu'un ordre géométrique exceptionnel commence à se voir à travers lui.