Il y a deux hommes nommés "Van Eck". Le premier, en 1985, a montré au monde comment intercepter des données d'un moniteur (
phreaking Van Eck ) pour 15 $, le second, en 2010, a proposé une séquence astucieuse (séquence de
Van Eck ). Plus raide que la simplicité de la tâche de cette séquence ne peut être que ses propriétés et ses énigmes.
Donc, l'algorithme pour générer des membres de séquence. Nous prenons le "numéro de départ", par exemple, "0", écrivez. Le terme suivant est le nombre de pas en arrière que ce nombre s'est produit dans la sous-séquence précédente. Si jamais, écrivez zéro. Le suivant est le nombre de pas en arrière il y avait zéro dans la sous-séquence précédente, c'est-à-dire un pas en arrière. Nous notons l'unité. Unité un - écrire zéro. Oups, zéro a reculé de deux pas. Nous écrivons deux, et ainsi de suite ...
Pour le point de rapport «0», les 97 premiers membres de la séquence:
0, 0, 1, 0, 2, 0, 2, 2, 1, 6, 0, 5, 0, 2, 6, 5, 4, 0, 5, 3, 0, 3, 2, 9, 0, 4, 9, 3, 6, 14, 0, 6, 3, 5, 15, 0, 5, 3, 5, 2, 17, 0, 6, 11, 0, 3, 8, 0, 3, 3, 1, 42, 0, 5, 15, 20, 0, 4, 32, 0, 3, 11, 18, 0, 4, 7, 0, 3, 7, 3, 2, 31, 0, 6, 31, 3, 6, 3, 2, 8, 33, 0, 9, 56, 0, 3, 8, 7, 19, 0, 5, 37, 0, 3, 8, 8, 1
Graphique:
Encore plus de chronologie:
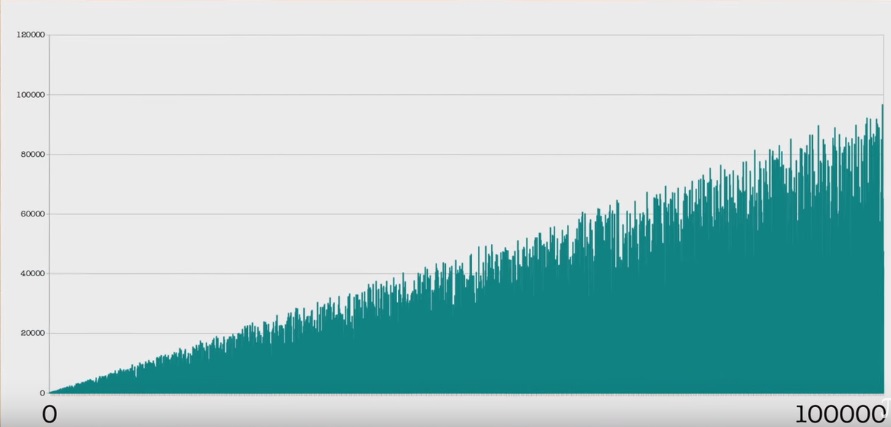
Les propriétés d'une séquence sont assez facilement prouvées que son terme maximum augmente tout le temps et qu'elle a un nombre infini de zéros. Ou qu'il n'y a pas de périodes. (Quelques théorèmes et conséquences
ici .)
Graphique logarithmique:
Programme en Python:
A181391 = [0] last_pos = {} for i in range(10**4): new_value = i - last_pos.get(A181391[i], i) A181391.append(new_value) last_pos[A181391[i]] = i
Pour le nombre de départ "1", la première centaine est:
1, 0, 0, 1, 3, 0, 3, 2, 0, 3, 3, 1, 8, 0, 5, 0, 2, 9, 0, 3, 9, 3, 2, 6, 0, 6, 2, 4, 0, 4, 2, 4, 2, 2, 1, 23, 0, 8, 25, 0, 3, 19, 0, 3, 3, 1, 11, 0, 5, 34, 0, 3, 7, 0, 3, 3, 1, 11, 11, 1, 3, 5, 13, 0, 10, 0, 2, 33, 0, 3, 9, 50, 0, 4, 42, 0, 3, 7, 25, 40, 0, 5, 20, 0, 3, 8, 48, 0, 4, 15
Graphique:
Pour le nombre de départ "2", la première centaine est:
2, 0, 0, 1, 0, 2, 5, 0, 3, 0, 2, 5, 5, 1, 10, 0, 6, 0, 2, 8, 0, 3, 13, 0, 3, 3, 1, 13, 5, 16, 0, 7, 0, 2, 15, 0, 3, 11, 0, 3, 3, 1, 15, 8, 24, 0, 7, 15, 5, 20, 0, 5, 3, 12, 0, 4, 0, 2, 24, 14, 0, 4, 6, 46, 0, 4, 4, 1, 26, 0, 5, 19, 0, 3, 21, 0, 3, 3, 1, 11, 42, 0, 6, 20, 34, 0, 4, 20, 4
Graphique:
Les sources