Nouveau service d'indices pour rechercher hh.ru

Les indices de recherche sont excellents. À quelle fréquence tapons-nous l'adresse complète du site dans la barre d'adresse? Et le nom du produit dans la boutique en ligne? Pour des requêtes aussi courtes, il suffit généralement de taper quelques caractères si les indices de recherche sont bons. Et si vous n'avez pas vingt doigts ou une vitesse de frappe incroyable, vous les utiliserez sûrement.
Dans cet article, nous parlerons de notre nouveau service d'indices de recherche hh.ru, ce que nous avons fait dans le numéro précédent de la School of Programmers .

L'ancien service avait un certain nombre de problèmes:

• il a travaillé sur des requêtes d'utilisateurs populaires sélectionnées à la main;
• n'a pas pu s'adapter à l'évolution des préférences des utilisateurs;
• n'a pas pu classer les requêtes qui ne sont pas incluses dans le haut;
• n'a pas corrigé les fautes de frappe.

Dans le nouveau service, nous avons corrigé ces lacunes (tout en en ajoutant de nouvelles).

Dictionnaire des requêtes populaires

Lorsqu'il n'y a aucun indice, vous pouvez sélectionner manuellement les requêtes N des utilisateurs et générer des indices à partir de ces requêtes en utilisant l'occurrence exacte des mots (avec ou sans ordre). C'est une bonne option - elle est facile à mettre en œuvre, donne une bonne précision des invites et ne rencontre pas de problèmes de performances. Pendant longtemps, notre conseil a fonctionné comme ça, mais un inconvénient important de cette approche est le caractère incomplet de l'émission.

Par exemple, la demande "développeur javascript" ne faisait pas partie de cette liste. Par conséquent, lorsque nous saisissons "heures javascript", nous n'avons rien à afficher. Si nous complétons la demande, en ne prenant en compte que le dernier mot, nous verrons "bricoleur javascript" en premier lieu. Pour la même raison, il ne sera pas possible d'implémenter une correction d'erreur plus difficile que l'approche standard avec la recherche des mots les plus proches par distance Damerau-Levenshtein.

Modèle de langage

Une autre approche consiste à apprendre à évaluer les probabilités de requêtes et à générer les suites les plus probables pour une requête utilisateur. Pour ce faire, utilisez des modèles de langage - une distribution de probabilité sur un ensemble de séquences de mots.



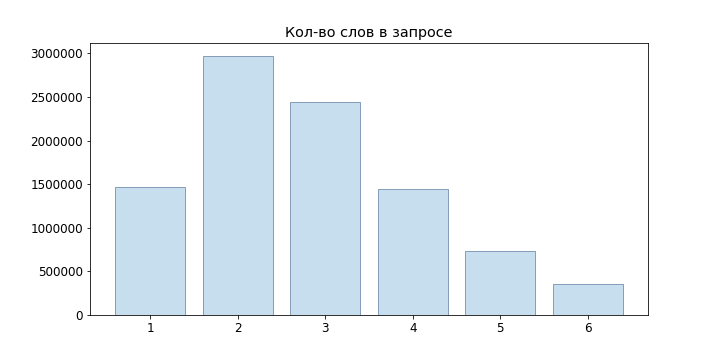
Étant donné que les demandes des utilisateurs sont généralement courtes, nous n'avons même pas essayé les modèles de langage de réseau neuronal, mais nous nous sommes limités à n-gram:

$$

$$P (w_1 \ dots w_m) = \ prod_ {i = 1} ^ mP (w_i | w_1 \ dots w_ {i-1}) \ approx \ prod_ {i = 1} ^ mP (w_i | w_ {i- ( n-1)} \ points w_ {i-1})$$

En tant que modèle le plus simple, nous pouvons prendre la définition statistique de la probabilité, puis

$$

$$P (w_i | w_1 \ dots w_ {i-1}) = \ frac {count (w_1 \ dots w_i)} {count (w_1 \ dots w_ {i-1})}$$

Cependant, un tel modèle ne convient pas pour évaluer des requêtes qui n'étaient pas dans notre échantillon: si nous n'avons pas observé le `` Java Developer Junior '', il s'avère que

$$

$$P (\ text {développeur junior java}) = \ frac {count (\ text {développeur junior java})} {count (\ text {développeur junior})} = 0$$

Pour résoudre ce problème, vous pouvez utiliser différents modèles de lissage et d'interpolation. Nous avons utilisé Backoff:

$$

$$P_ {bo} (w_n | w_1 \ dots w_ {n-1}) = \ begin {cases} {P} (w_n | w_1 \ dots w_ {n-1}), count (w_1 \ dots w_ {n- 1})> 0 \\ \ alpha {P_ {bo}} (w_n | w_2 \ dots w_ {n-1}), count (w_1 \ dots w_ {n-1}) = 0 \ end {cases}$$

$$

$$\ alpha = \ frac {P (w_1 \ dots w_ {n-1})} {1 - \ sum_wP_ {bo} (w | w_2 \ dots w_ {n-1})}$$

Où P est la probabilité lissée $$$w_1 ... w_ {n-1}$ (nous avons utilisé le lissage de Laplace):

$$

$$P (w_n | w_1 \ points w_ {n-1}) = \ frac {count (w_n) + \ delta} {count (w_1 \ dots w_ {n-1}) + \ delta | V |}$$

où V est notre dictionnaire.

Génération d'options

Nous sommes donc en mesure d'évaluer la probabilité d'une demande particulière, mais comment générer ces mêmes demandes? Il est judicieux de procéder comme suit: laisser l'utilisateur entrer une requête $$$w_1 ... w_n$ , les requêtes qui nous conviennent peuvent être trouvées à partir de la condition

$$

$$w_1 \ dots w_m = \ underset {w_ {n + 1} \ dots w_m \ in V} {argmax} P (w_1 \ dots w_n w_ {n + 1} \ dots w_m)$$

Bien sûr, le tri $$$| V | ^ {m-n}, m = 1 \ points M$ Il n'est pas possible de sélectionner les meilleures options pour chaque demande entrante, nous utiliserons donc la recherche de faisceaux . Pour notre modèle de langage n-gram, cela se résume à l'algorithme suivant:

def beam(initial, vocabulary): variants = [initial] for i in range(P): candidates = [] for variant in variants: candidates.extends(generate_candidates(variant, vocabulary)) variants = sorted(candidates)[:N] return candidates def generate_candidates(variant, vocabulary): top_terms = [] #         1, 2, ... n  for n0 in range(n): top_n = sorted(vocabulary, key=lambda c: P(|variant[-n0:]) top_terms.extends(top_n) candidates = [variant + [term] for term in top_terms] #       candidates = sorted(candidates, key=lambda v: P(variant))[:N] return candidates 

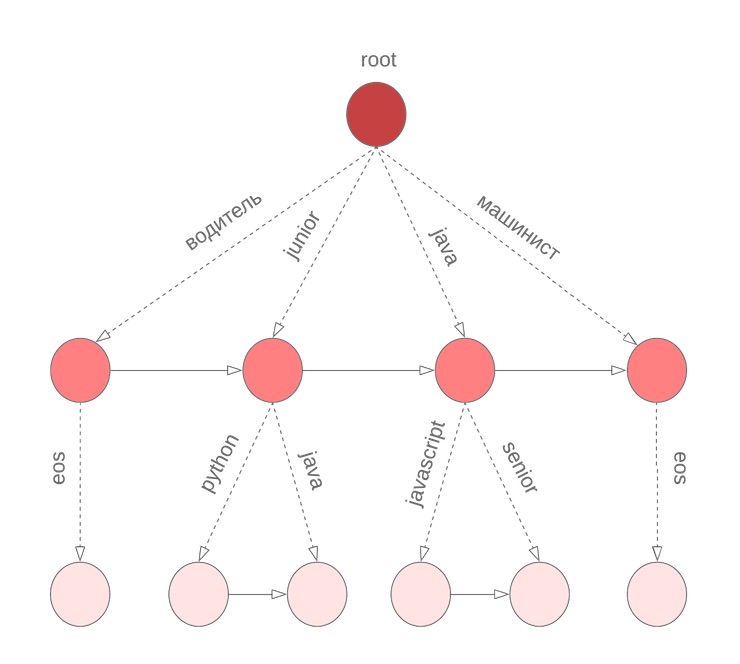
Ici, les nœuds surlignés en vert sont les dernières options sélectionnées, le nombre devant le nœud $$$w_n$ - probabilité $$$P (w_n | w_ {n-1})$ , après le nœud - $$$P (w1 ... w_n)$ .

C'est devenu beaucoup mieux, mais dans generate_candidates, vous devez obtenir rapidement N meilleurs termes pour un contexte donné. Dans le cas du stockage uniquement des probabilités de n-grammes, nous devons parcourir l'intégralité du dictionnaire, calculer les probabilités de toutes les phrases possibles, puis les trier. De toute évidence, cela ne décollera pas pour les requêtes en ligne.

Bore pour les probabilités

Pour obtenir rapidement le meilleur N dans les variantes de probabilité conditionnelle de la continuation de la phrase, nous avons utilisé le bore en termes. Dans le nœud $$$w_1 \ à w_2$ coefficient enregistré $$$\ alpha$ , valeur $$$P (w_2 | w_1)$ et triés par probabilité conditionnelle $$$P (\ bullet | w_1 w_2)$ liste des termes $$$w_3$ avec $$$P (w_3 | w_1 w_2)$ . Le terme spécial eos marque la fin d'une phrase.

Mais il y a une nuance

Dans l'algorithme décrit ci-dessus, nous supposons que tous les mots de la requête ont été complétés. Cependant, ce n'est pas vrai pour le dernier mot que l'utilisateur saisit en ce moment. Nous devons à nouveau parcourir tout le dictionnaire pour continuer le mot en cours de saisie. Pour résoudre ce problème, nous utilisons un bore symbolique, dans les nœuds dont nous stockons M termes triés par la probabilité unigramme. Par exemple, cela ressemblera à notre bor pour java, junior, jupyter, javascript avec M = 3:



Ensuite, avant de commencer la recherche de faisceaux, nous trouvons les M meilleurs candidats pour continuer le mot actuel $$$w_n$ et sélectionner les N meilleurs candidats pour $$$P (w_1 \ points w_n)$ .

Typos

Eh bien, nous avons construit un service qui vous permet de donner de bons conseils pour une demande d'utilisateur. Nous sommes même prêts pour de nouveaux mots. Et tout irait bien ... Mais les utilisateurs font attention et ne changent pas les claviers hfcrkflre.

Comment résoudre ça? La première chose qui me vient à l'esprit est la recherche de corrections en trouvant les options les plus proches pour la distance Damerau-Levenshtein, qui est définie comme le nombre minimum d'insertion / suppression / remplacement d'un caractère ou transposition de deux caractères voisins nécessaires pour en obtenir un autre à partir d'une ligne. Malheureusement, cette distance ne prend pas en compte la probabilité d'un remplacement particulier. Ainsi, pour le mot saisi «sapeur», nous obtenons que les options «collecteur» et «soudeur» sont équivalentes, bien qu'il semble intuitivement qu'elles signifient le deuxième mot.

Le deuxième problème est que nous ne prenons pas en compte le contexte dans lequel l'erreur s'est produite. Par exemple, dans la requête «sapeur de commandes», nous préférons toujours l'option «collecteur» plutôt que «soudeur».

Si vous abordez la tâche de corriger les fautes de frappe d'un point de vue probabiliste, il est tout à fait naturel d'arriver à un modèle de canal bruyant :

1. ensemble alphabet $$$\ Sigma$ ;
2. ensemble de toutes les lignes de fuite $$$\ Sigma ^ *$ sur lui;
3. beaucoup de lignes qui sont des mots corrects $$$D \ subseteq \ Sigma ^ *$ ;
4. distributions données $$$P (s | w)$ où $$$s \ in \ Sigma ^ *, w \ in D$ .

Ensuite, la tâche de correction est définie comme la recherche du mot correct w pour l'entrée s. Selon la source de l'erreur, mesurez $$$P$ il peut être construit de différentes manières, dans notre cas, il est sage d'essayer d'estimer la probabilité de fautes de frappe (appelons-les remplacements élémentaires) $$$P_e (t | r)$ , où t, r sont des n-grammes symboliques, puis évaluent $$$P (s | w)$ comme la probabilité d'obtenir s de w par les remplacements élémentaires les plus probables.

Soit $$$Part_n (x)$ - fractionner la chaîne x en n sous-chaînes (éventuellement zéro). Le modèle de Brill-Moore implique le calcul de la probabilité $$$P (s | w)$ comme suit:

$$

$$P (s | w) \ approx \ max_ {R \ in Part_n (s)} T \ in Part_n (s)} \ prod_ {i = 1} ^ {n} P_e (T_i | R_i)$$

Mais nous devons trouver $$$P (w | s)$ :

$$

$$P (w | s) = \ frac {P (s | w) P (w)} {P (s)} = const \ cdot P (s | w) \ cdot P (w)$$

En apprenant à évaluer P (w | s), nous résoudrons également le problème des options de classement avec la même distance Damerau-Levenshtein et pouvons prendre en compte le contexte lors de la correction d'une faute de frappe.

Calcul $$$P_e (T_i | R_i)$

Pour calculer les probabilités de substitutions élémentaires, les requêtes des utilisateurs nous aideront à nouveau: nous composerons des paires de mots (s, w) qui

1. fermer à Damerau-Levenshtein;
2. l'un des mots est plus courant que les autres N fois.

Pour de telles paires, nous considérons l'alignement optimal selon Levenshtein:


Nous composons toutes les partitions possibles de s et w (nous nous sommes limités aux longueurs n = 2, 3): n → n, pr → rn, pro → rn, ro → po, m → ``, mm → m, etc. Pour chaque n-gramme, on trouve

$$

$$P_e (t | r) = \ frac {count (r \ to t)} {count (r)}$$

Calcul $$$P (s | w)$

Calcul $$$P (s | w)$ prend directement $$$O (2 ^ {| w | + | s |})$ : nous devons trier toutes les partitions possibles de w avec toutes les partitions possibles de s. Cependant, la dynamique sur le préfixe peut donner une réponse pour $$$O (| w | * | s | * n ^ 2)$ où n est la longueur maximale des substitutions élémentaires:

$$

$$d [i, j] = \ begin {cases} d [0, j] = 0 & j> = k \\ d [i, 0] = 0 & i> = k \\ d [0, j] = P (s [0: j] \ espace | \ espace w [0]) & j <k \\ d [i, 0] = P (s [0] \ espace | \ espace w [0: i]) & i <k \\ d [i, j] = \ underset {k, l \ le n, k \ lt i, l \ lt j} {max} (P (s [jl: j] \ space | \ space w [ik: i]) \ cdot d [ik-1, jl-1]) \ end {cases}$$

Ici, P est la probabilité de la ligne correspondante dans le modèle k-gramme. Si vous regardez de plus près, il est très similaire à l'algorithme de Wagner-Fisher avec écrêtage Ukkonen. À chaque étape, nous obtenons $$$P (w [0: i] | s [0: j])$ en énumérant toutes les corrections $$$w [i-k: i]$ dans $$$s [j-l: j]$ sous réserve de $$$k, l \ le n$ et le choix du plus probable.

Retour à $$$P (w | s)$

Ainsi, nous pouvons calculer $$$P (s | w)$ . Maintenant, nous devons sélectionner plusieurs options en maximisant $$$P (w | s)$ . Plus précisément, pour la demande d'origine $$$s_1s_2 \ dots s_n$ tu dois choisir $$$w_1 \ dots w_n$ où $$$P (w_1 \ points w_n | s_1 \ points s_n)$ maximum. Malheureusement, un choix honnête d'options ne correspondait pas à nos exigences de temps de réponse (et la date limite du projet touchait à sa fin), nous avons donc décidé de nous concentrer sur l'approche suivante:

1. à partir de la requête d'origine, nous obtenons plusieurs options en changeant les k derniers mots:
   
   1. nous corrigeons la disposition du clavier si le terme résultant a une probabilité plusieurs fois supérieure à celle d'origine;
   2. on trouve des mots dont la distance Damerau-Levenshtein ne dépasse pas d;
   3. choisissez parmi les options top-N pour $$$P (s | w)$ ;
2. envoyer BeamSearch à l'entrée avec la demande d'origine;
3. lors du classement des résultats, nous actualisons les options obtenues sur $$$\ prod_ {i = 0} ^ {k-1} P (s_ {n-i} | w_ {n-i})$ .

Pour l'élément 1.2, nous avons utilisé l'algorithme FB-Trie (tri avant et arrière), basé sur une recherche floue dans les arbres de préfixe avant et arrière. Cela s'est avéré plus rapide que l'évaluation de P (s | w) dans le dictionnaire.

Statistiques de requête

Avec la construction du modèle de langage, tout est simple: nous collectons des statistiques sur les requêtes des utilisateurs (combien de fois nous avons fait une demande pour une phrase donnée, combien d'utilisateurs, combien d'utilisateurs enregistrés), nous avons divisé les demandes en n-grammes et construit des fraises. Plus compliqué avec le modèle d'erreur: au minimum, un dictionnaire des bons mots est nécessaire pour le construire. Comme mentionné ci-dessus, pour sélectionner les paires d'entraînement, nous avons utilisé l'hypothèse que ces paires devraient être proches dans la distance Damerau-Levenshtein, et l'une devrait se produire plus souvent que l'autre plusieurs fois.

Mais les données sont encore trop bruyantes: tentatives d'injection xss, mise en page incorrecte, texte aléatoire du presse-papiers, utilisateurs expérimentés avec des requêtes "programmeur c pas 1c", requêtes du chat qui sont passées par le clavier .


Par conséquent, pour effacer les données source, nous avons exclu:

• termes de basse fréquence;
• Contenant des opérateurs de langage de requête
• vocabulaire obscène.

Ils ont également corrigé la disposition du clavier, vérifié les mots des textes des postes vacants et ouvert les dictionnaires. Bien sûr, il n'a pas été possible de tout réparer, mais ces options sont généralement soit complètement coupées, soit situées en bas de la liste.

En prod

Juste avant la protection du projet, ils ont lancé un service en production pour les tests internes, et après quelques jours - pour 20% des utilisateurs. Dans hh.ru, toutes les modifications importantes pour les utilisateurs passent par un système de tests AB , ce qui nous permet non seulement d'être sûr de la signification et de la qualité des modifications, mais aussi de trouver des erreurs .



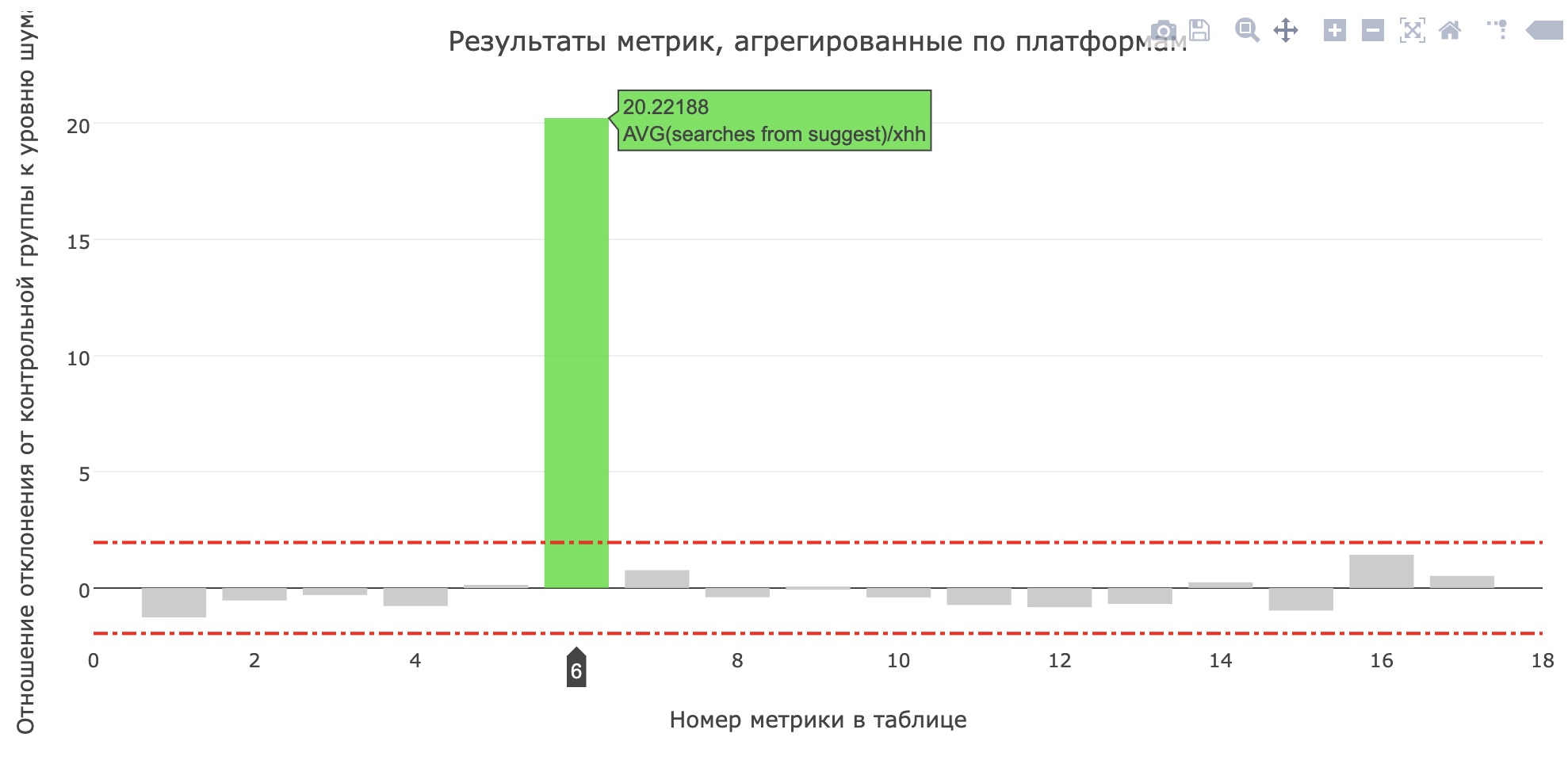
La mesure du nombre moyen de recherches à partir de la requête pour les candidats s'est améliorée (passant de 0,959 à 1,1355), et la part des recherches à partir de toutes les requêtes de recherche est passée de 12,78% à 15,04%. Malheureusement, les principales mesures du produit n'ont pas augmenté, mais les utilisateurs ont certainement commencé à utiliser plus de conseils.

En fin de compte

Il n'y avait pas de place pour une histoire sur les processus de l'école, les autres modèles testés, les outils que nous avons écrits pour les comparaisons de modèles et les réunions où nous avons décidé quelles fonctionnalités développer afin de réaliser une démo intermédiaire. Regardez les dossiers de l'école passée , laissez une demande sur https://school.hh.ru , remplissez des tâches intéressantes et venez étudier. Soit dit en passant, le service de vérification des tâches a également été effectué par les diplômés de l'ensemble précédent.

Que lire?

1. Introduction au modèle de langage
2. Modèle Brill-Moore
3. Fb-trie
4. Qu'advient-il de votre requête de recherche