Le livre "Grok deep learning"

Salut, habrozhiteli! Le livre jette les bases d'une maîtrise accrue des technologies d'apprentissage en profondeur. Il commence par une description des bases des réseaux de neurones, puis examine en détail les couches d'architecture supplémentaires.

Le livre est spécialement écrit dans le but de fournir le seuil d'entrée le plus bas possible. Vous n'avez pas besoin de connaître l'algèbre linéaire, les méthodes numériques, les optimisations convexes et même l'apprentissage automatique. Tout ce qui est nécessaire pour comprendre l'apprentissage en profondeur sera clarifié au fur et à mesure.

Nous vous proposons de vous familiariser avec le passage "Qu'est-ce qu'un cadre d'apprentissage en profondeur?"

De bons outils réduisent les erreurs, accélèrent le développement et augmentent la vitesse d'exécution.

Si vous lisez beaucoup sur l'apprentissage en profondeur, vous êtes probablement tombé sur des cadres bien connus tels que PyTorch, TensorFlow, Theano (récemment déclaré obsolète), Keras, Lasagne et DyNet. Au cours des dernières années, les frameworks ont évolué très rapidement, et malgré le fait que tous ces frameworks soient distribués gratuitement et open source, chacun d'eux a un esprit de compétition et de camaraderie.

Jusqu'à présent, j'ai évité de discuter de frameworks, car, tout d'abord, il était extrêmement important pour vous de comprendre ce qui se passait en coulisses, en implémentant les algorithmes manuellement (en utilisant uniquement la bibliothèque NumPy). Mais maintenant, nous allons commencer à utiliser de tels cadres, car les réseaux que nous allons former, les réseaux avec mémoire à court terme à long terme (LSTM), sont très complexes, et le code qui les implémente en utilisant NumPy est difficile à lire, à utiliser et à déboguer (gradients dans ce code se trouvent partout).

C'est cette complexité que les cadres d'apprentissage en profondeur sont conçus pour traiter. Le cadre d'apprentissage en profondeur peut réduire considérablement la complexité du code (ainsi que le nombre d'erreurs et augmenter la vitesse de développement) et augmenter la vitesse de son exécution, surtout si vous utilisez un processeur graphique (GPU) pour entraîner le réseau neuronal, ce qui peut accélérer le processus de 10 à 100 fois. Pour ces raisons, les cadres sont utilisés presque partout dans la communauté de la recherche, et la compréhension des caractéristiques de leur travail vous sera utile dans votre carrière en tant qu'utilisateur et chercheur en apprentissage profond.

Mais nous ne nous limiterons pas au cadre d'un cadre particulier, car cela vous empêchera d'apprendre comment fonctionnent tous ces modèles complexes (tels que LSTM). Au lieu de cela, nous allons créer notre propre framework léger, en suivant les dernières tendances dans le développement de frameworks. En suivant ce chemin, vous saurez exactement ce que font les frameworks lorsque des architectures complexes sont créées avec leur aide. De plus, une tentative de créer votre propre petit framework vous-même vous aidera à passer en douceur à l'utilisation de véritables frameworks d'apprentissage en profondeur, car vous connaissez déjà les principes d'organisation d'une interface de programme (API) et ses fonctionnalités. Cet exercice m'a été très utile et les connaissances acquises lors de la création de mon propre framework se sont avérées très utiles lors du débogage de modèles de problème.

Comment le framework simplifie-t-il le code? En termes abstraits, cela élimine la nécessité d'écrire encore et encore le même code. Plus précisément, la fonctionnalité la plus pratique du cadre d'apprentissage en profondeur est la prise en charge de la rétropropagation automatique et de l'optimisation automatique. Cela vous permet d'écrire uniquement du code de distribution directe, et le framework se chargera automatiquement de la distribution arrière et de la correction des poids. La plupart des frameworks modernes simplifient même le code qui implémente la distribution directe en offrant des interfaces de haut niveau pour définir des couches typiques et des fonctions de perte.

Introduction aux tenseurs

Les tenseurs sont une forme abstraite de vecteurs et de matrices

Jusqu'à ce moment, nous utilisions des vecteurs et des matrices comme structures principales. Permettez-moi de vous rappeler qu'une matrice est une liste de vecteurs, et un vecteur est une liste de scalaires (nombres simples). Un tenseur est une forme abstraite pour représenter des listes de nombres imbriquées. Le vecteur est un tenseur unidimensionnel. La matrice est un tenseur à deux dimensions, et les structures avec un grand nombre de dimensions sont appelées tenseurs à n dimensions. Commençons donc à créer un nouveau cadre d'apprentissage en profondeur en définissant un type de base, que nous appellerons Tenseur:

import numpy as np class Tensor (object): def __init__(self, data): self.data = np.array(data) def __add__(self, other): return Tensor(self.data + other.data) def __repr__(self): return str(self.data.__repr__()) def __str__(self): return str(self.data.__str__()) x = Tensor([1,2,3,4,5]) print(x) [1 2 3 4 5] y = x + x print(y) [2 4 6 8 10] 

Ceci est la première version de notre structure de données de base. Notez qu'il stocke toutes les informations numériques dans le tableau NumPy (self.data) et prend en charge une opération de tenseur unique (ajout). Ajouter des opérations supplémentaires n'est pas difficile du tout, ajoutez simplement des fonctions supplémentaires avec la fonctionnalité correspondante à la classe Tensor.

Introduction au calcul automatique du gradient (autograd)

Auparavant, nous avons effectué une propagation arrière manuelle. Maintenant, rendons-le automatique!

Dans le chapitre 4, nous avons introduit les dérivés. Depuis lors, nous avons calculé manuellement ces dérivées dans chaque nouveau réseau neuronal. Permettez-moi de vous rappeler que cela est réalisé par un mouvement inverse à travers le réseau de neurones: d'abord, le gradient à la sortie du réseau est calculé, puis ce résultat est utilisé pour calculer la dérivée dans le composant précédent, et ainsi de suite, jusqu'à ce que les gradients corrects soient déterminés pour tous les poids dans l'architecture. Cette logique de calcul des gradients peut également être ajoutée à la classe des tenseurs. Ce qui suit montre ce que j'avais en tête.

 import numpy as np class Tensor (object): def __init__(self, data, creators=None, creation_op=None): self.data = np.array(data) self.creation_op = creation_op self.creators = creators self.grad = None def backward(self, grad): self.grad = grad if(self.creation_op == "add"): self.creators[0].backward(grad) self.creators[1].backward(grad) def __add__(self, other): return Tensor(self.data + other.data, creators=[self,other], creation_op="add") def __repr__(self): return str(self.data.__repr__()) def __str__(self): return str(self.data.__str__()) x = Tensor([1,2,3,4,5]) y = Tensor([2,2,2,2,2]) z = x + y z.backward(Tensor(np.array([1,1,1,1,1]))) 

Cette méthode introduit deux innovations. Tout d'abord, chaque tenseur reçoit deux nouveaux attributs. creators est une liste de tous les tenseurs utilisés pour créer le tenseur actuel (par défaut None). Autrement dit, si le tenseur z est obtenu en ajoutant les deux autres tenseurs, x et y, l'attribut creators du tenseur z contiendra les tenseurs x et y. creation_op est un attribut compagnon qui stocke les opérations utilisées dans le processus de création de ce tenseur. Autrement dit, l'instruction z = x + y créera un graphe de calcul avec trois nœuds (x, y et z) et deux arêtes (z -> x et z -> y). Chaque bord est signé par l'opération de creation_op, c'est-à-dire ajouter. Ce graphique aidera à organiser la propagation récursive vers l'arrière des gradients.


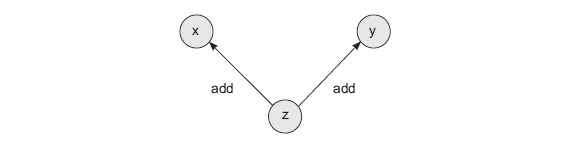
La première innovation de cette implémentation est la création automatique d'un graphe lors de chaque opération mathématique. Si nous prenons z et effectuons une autre opération, le graphe sera poursuivi dans une nouvelle variable référençant z.

La deuxième innovation de cette version de la classe Tensor est la possibilité d'utiliser un graphique pour calculer les gradients. Si vous appelez la méthode z.backward (), elle passera le gradient pour x et y, en tenant compte de la fonction avec laquelle le tenseur z (add) a été créé. Comme le montre l'exemple ci-dessus, nous passons le vecteur de gradient (np.array ([1,1,1,1,1]]) à z, et que l'on applique à ses parents. Comme vous vous en souvenez probablement du chapitre 4, la propagation vers l'arrière par l'addition signifie appliquer la propagation vers l'arrière. Dans ce cas, nous n'avons qu'un seul gradient à ajouter à x et y, nous le copions donc de z à x et y:

 print(x.grad) print(y.grad) print(z.creators) print(z.creation_op) [1 1 1 1 1] [1 1 1 1 1] [array([1, 2, 3, 4, 5]), array([2, 2, 2, 2, 2])] add 

La caractéristique la plus remarquable de cette forme de calcul automatique du gradient est qu'elle fonctionne récursivement - chaque vecteur appelle la méthode .backward () de tous ses parents à partir de la liste self.creators:


»Plus d'informations sur le livre sont disponibles sur le site Web de l'éditeur
» Contenu
» Extrait

25% de réduction sur les colporteurs - Deep Learning
Lors du paiement de la version papier du livre, un livre électronique est envoyé par e-mail.