Que devez-vous faire si vous avez besoin de dessiner un graphique, mais les outils qui se trouvent sous votre bras dessinent une sorte de masse de cheveux ou même dévorent toute la RAM et raccrochent le système? Au cours des deux dernières années de travail avec de grands graphiques (des centaines de millions de sommets et d'arêtes), j'ai essayé de nombreux outils et approches, et je n'ai presque pas trouvé de critiques décentes. Par conséquent, maintenant j'écris moi-même une telle critique.
Pourquoi visualiser des graphiques?
Trouvez quoi chercher
À l'entrée, nous avons généralement juste un ensemble de sommets et d'arêtes, qui est essentiellement un graphique. Nous pouvons calculer certaines caractéristiques statistiques, des mesures de graphique à partir de celui-ci, mais cela ne vous donnera pas une image claire de ce que c'est. Une bonne visualisation peut montrer s'il y a un amas ou des ponts dans le graphique, ou est-il homogène, ou peut-être qu'il fusionne en un bloc à un centre d'attraction majeur.
Se vanter
La visualisation des données, par définition, résout le problème de représentation. Si certains travaux ont déjà été effectués, vous pouvez montrer les conclusions dans une image spectaculaire. Par exemple, si vous avez regroupé un graphique, vous pouvez coloriser le graphique en grappes et montrer comment les différentes étiquettes sont liées les unes aux autres.
Obtenez des signes
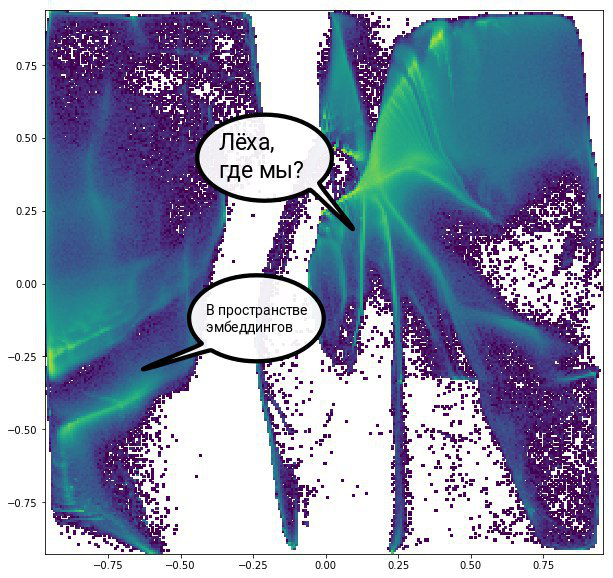
Bien que les algorithmes de visualisation de graphes aient été principalement développés uniquement comme des outils pour obtenir des images, ils peuvent être utilisés comme méthodes de réduction de la dimension. Le graphique lui-même, s'il est représenté par une matrice d'adjacence, est des données dans un espace de grande dimension, et lors du rendu, nous obtenons deux coordonnées pour chaque sommet (parfois trois ou plus, mais c'est une exception). La proximité des sommets dans la visualisation exprime souvent la similitude des propriétés.
Quel est le problème avec les grands graphiques?
Par grands graphiques, j'entendrai des dimensions, disons, à partir de 10 000 sommets ou arêtes. Pour les petites tailles, il n'y a généralement pas de problèmes, car presque tous les outils que l'on peut trouver par une recherche rapide sur Internet résolvent bien leurs problèmes pour de tels volumes. Quel est le problème avec les grands graphiques? Deux problèmes: c'est la lisibilité et la vitesse. Il est prévu que plus il y aura d'objets, plus il sera difficile de les naviguer. Pour les grands graphiques, on obtient souvent des images impossibles à comprendre. De plus, les algorithmes de graphes sont généralement très lents, beaucoup ont une complexité algorithmique proportionnelle au carré (parfois cube) du nombre de sommets et / ou d'arêtes. Même si vous attendez le rendu, vous ne pouvez toujours pas vous permettre de passer par de nombreuses options pour obtenir un résultat satisfaisant.
Qu'est-ce que différentes personnes intelligentes écrivent à ce sujet?
Il y a quelques œuvres sur lesquelles je voudrais attirer l'attention:
[1] Helen Gibson, Joe Faith et Paul Vickers: «Une étude des techniques de mise en page graphique bidimensionnelle pour la visualisation de l'information»Les gars trient d'abord les approches pour dessiner des graphiques, expliquent les principes de travail, puis essaient de les essayer tous. Il y a un tableau très détaillé avec des informations sur différents algorithmes, y compris leur complexité algorithmique.
[2] Oh-Hyun Kwon, Tarik Crnovrsanin et Kwan-Liu Ma «À quoi ressemblerait un graphique dans cette présentation? Une approche d'apprentissage automatique pour la visualisation de grands graphes »Ici, nos camarades sont devenus très confus et ont obtenu toutes les implémentations d'algorithmes de visualisation de graphiques qu'ils pouvaient. Ensuite, ils ont visualisé de nombreux graphiques et donné des marqueurs pour le balisage. Selon les résultats, nous avons appris au modèle à évaluer à quoi ressemblera le graphique dans différentes options de style. J'ai pris quelques photos de cet article.
Théorie
L'empilement est un moyen de mapper les coordonnées à chaque sommet d'un graphique. Habituellement, nous parlons de coordonnées sur un plan, bien que de manière générale il ne soit pas nécessaire que ce soit un plan. Utiliser simplement plus de 2 dimensions n'est presque jamais nécessaire.
Qu'est-ce qu'un bon style?

Il est très facile de dire que quelque chose semble bon ou mauvais, mais il est difficile d'expliquer à la machine comment donner une telle évaluation. Pour faire un «bon» style, les métriques dites «esthétiques» sont généralement optimisées et formulées de manière plus objective. En voici quelques uns:
Traversée minimale des côtesC'est simple: quand il y a beaucoup d'intersections, il s'avère "bouillie", quand ce n'est pas suffisant, alors l'image a l'air "plus propre"
Les pics adjacents sont proches les uns des autres, les non-adjacents sont loin.Un graphique par définition est un ensemble de connexions entre des sommets et un ensemble de sommets. Rendre les sommets connectés plus proches les uns des autres est un moyen direct et logique d'exprimer les propriétés de base des données de graphe.
Les communautés sont regroupéesCela découle du paragraphe précédent. S'il y a beaucoup de nœuds qui sont plus connectés les uns aux autres qu'au reste du graphique, ils forment une «communauté» et dans l'image devraient ressembler à un cluster dense
Superpositions minimales de sommets et d'arêtesAssez évident. Si nous ne pouvons pas distinguer un ou plusieurs objets ici, alors la visualisation est mal lue.
Répartir uniformément les sommets et / ou les arêtesCette condition est utile si les propriétés du graphe ne permettent pas de distinguer au moins une certaine structure autrement. Par exemple, si nous avons le graphique entier - il s'agit d'un cluster dense, alors il est préférable de le tacher dans l'image pour voir au moins l'inégalité des connexions plutôt que de lui permettre de fusionner en un point solide.
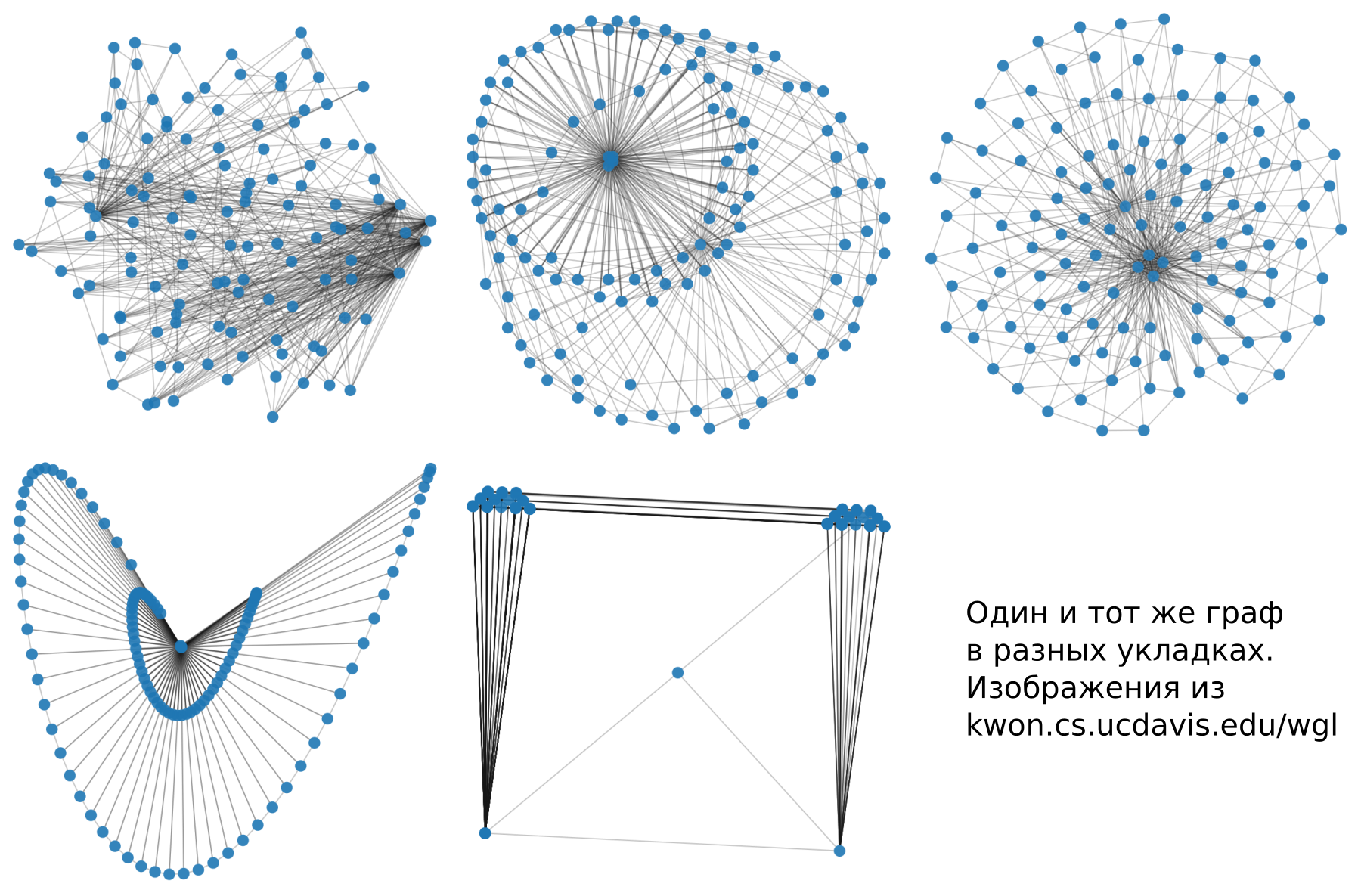
Quels sont le style
Je considère qu'il est important de considérer ces trois types de style, bien qu'il existe de nombreuses classifications et types. Cependant, la connaissance de ces types suffit pour naviguer sur le sujet.
- Force-dirigée et basée sur l'énergie
- Réduction de dimension
- Caractéristiques des nœuds
À force dirigée et à base d'énergie
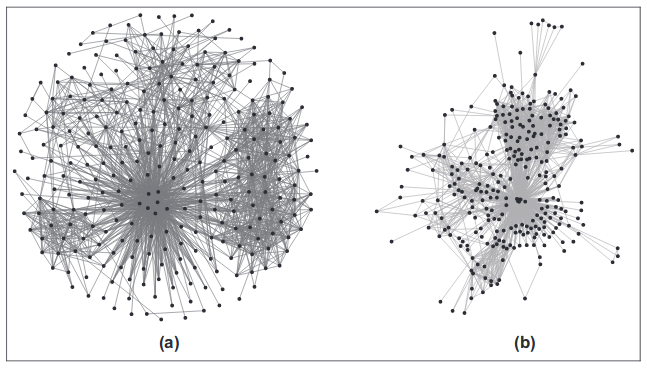
Ces méthodes utilisent une simulation de la force physique. Les pics sont représentés comme des particules chargées qui se repoussent et des bords - comme des cordes élastiques qui rassemblent les pics adjacents. Ensuite, le mouvement des sommets dans un tel système est simulé jusqu'à ce qu'un état stationnaire soit établi. D'autres approches tentent de décrire l'énergie potentielle d'un tel système et de trouver la position des sommets qui correspondront au minimum.
Les avantages de cette famille d'algorithmes comme image. Habituellement, on obtient un très bon style qui reflète la topologie du graphique. Inconvénients parmi les paramètres qui doivent être configurés. Eh bien et, bien sûr, la complexité de calcul. Pour chaque sommet, vous devez calculer les forces agissant à partir de tous les autres sommets.
Les algorithmes familiaux importants sont Force Atlas, Fruchterman-Reingold, Kamada Kawaii et OpenOrd. Ce dernier algorithme utilise des optimisations délicates, par exemple, coupe les bords longs pour accélérer les calculs, et comme effet secondaire, des grappes plus denses de pics proches sont obtenues.
Réduction de dimension

Le graphique peut être défini par la matrice d'adjacence, c'est-à-dire par la matrice carrée NxN, où N est le nombre de sommets. Cela peut être interprété comme N objets dans un espace de dimension N. Cette représentation permet l'utilisation de méthodes universelles de réduction de dimension, telles que tSNE, UMAP, PCA, etc. Une autre approche consiste à calculer les distances théoriques entre les sommets, sur la base des poids des arêtes et des connaissances de la topologie locale, puis à essayer de maintenir la relation entre ces distances lors du déplacement dans des espaces de plus petite dimension.
Disposition basée sur les fonctionnalités

Habituellement, les données proviennent du monde réel, où nous n'avons pas seulement des informations sur la contiguïté des sommets. Les pics sont des objets réels avec leurs propres propriétés. En gardant cela à l'esprit, nous pouvons utiliser les propriétés des sommets pour les afficher sur le plan. Pour ce faire, vous pouvez utiliser toutes les approches couramment utilisées pour les données tabulaires. Ce sont les méthodes de réduction des dimensions de PCA, UMAP, tSNE, Autoencoders déjà mentionnées ci-dessus. Ou vous pouvez dessiner un nuage de points simple (nuage de points) pour les paires d'entités et dessiner des bords déjà au-dessus de la vue résultante. Séparément, nous pouvons mentionner Hive Plot - une méthode intéressante lorsque les valeurs de l'attribut correspondent à différents axes dirigés depuis le centre, sur lesquels les sommets sont situés, et les bords sont dessinés par des arcs entre eux.
Outils de visualisation de grands graphes

Malgré le fait que la tâche de visualisation soit ancienne et relativement populaire, il existe de gros problèmes avec les outils pour les grands graphiques. La plupart d'entre eux ne sont pas pris en charge. Presque tout le monde a certaines de ses graves lacunes qui doivent être prises en charge. Je ne parlerai que de ceux qui méritent d'être mentionnés et qui peuvent être utilisés pour de grands graphiques. Pour les petits graphiques, il n'y a pas de problème - les outils sont faciles à trouver et fonctionnent bien.
GraphViz

Transactions et adresses de la blockchain Bitcoin jusqu'en 2011

La configuration des paramètres peut être difficile
Un outil CLI old-school avec son propre langage de description graphique - dot. En fait, c'est un package avec un style différent pour toute occasion. Pour les grands graphiques, il existe un outil sfdp - il appartient à la classe d'empilements Force Directed. Les avantages et les inconvénients de cet outil lors du lancement à partir de la ligne de commande. C'est très pratique pour la reproductibilité et l'automatisation, cependant, sans curseurs et affichage de résultats intermédiaires, le réglage des paramètres devient très douloureux. On définit les paramètres, on démarre, on attend sans barre de progression, on voit le résultat, on change les paramètres, on redémarre. Capable d'écrire en svg, png et autres formats d'image.
Gephi
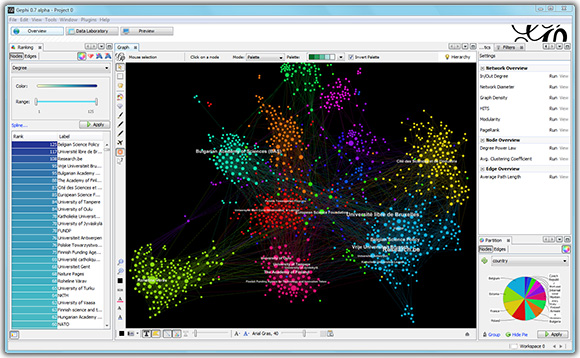

Recommandations 173 mille films avec iMDB

Plusieurs millions de pics est déjà une tâche trop difficile
Peut-être l'outil le plus puissant dans son intégralité. Il s'agit d'une application graphique qui contient un ensemble de styles de base, ainsi que de nombreux autres outils d'analyse graphique. La communauté gephi a écrit de nombreux plugins, comme mon Multigravity Force-Atlas 2 préféré ou un plugin pour exporter le style vers une page Web interactive. En outre, l'implémentation OpenOrd d'origine est contenue dans Gephi. Gephi dispose d'outils pour peindre les sommets et les arêtes en fonction de leurs propriétés, définir des légendes, des tailles et d'autres options de rendu. Il existe une exportation vers les principaux formats d'image, y compris le vecteur.
Un fait très ennuyeux est que Gephi est abandonné depuis plusieurs années. Les deux principaux développeurs, n'ayant pas les ressources nécessaires pour transférer à quelqu'un d'autre leurs connaissances nécessaires à leur développement, ont déclaré qu'ils ne pouvaient plus soutenir activement Gephi. D'autres inconvénients incluent une certaine «clarté» de l'interface et le manque de fonctionnalités évidentes, mais rien «n'est tout simplement mieux», personne n'a écrit. D'après les dernières nouvelles, une déclaration est apparue sur le blog du projet selon laquelle la puissance du WebGL moderne est déjà en avance sur l'ancien Gephi et il y a une chance de le voir revivre en tant qu'application Web.
igraph

Graphique de recommandation de musique dans lastfm. La source est
ici .
On ne peut que rendre hommage à ce progiciel à usage général pour l'analyse graphique. L'une des visualisations graphiques les plus spectaculaires de son époque a été réalisée par l'un des auteurs de igraph. Il a développé son style DrL pour cela. C'était un graphique des recommandations des bandes lastfm. Le résultat est plus élevé.
Les inconvénients incluent une documentation dégoûtante. Au moins pour l'api python. Il est plus facile de lire la source immédiatement.
LargeViz
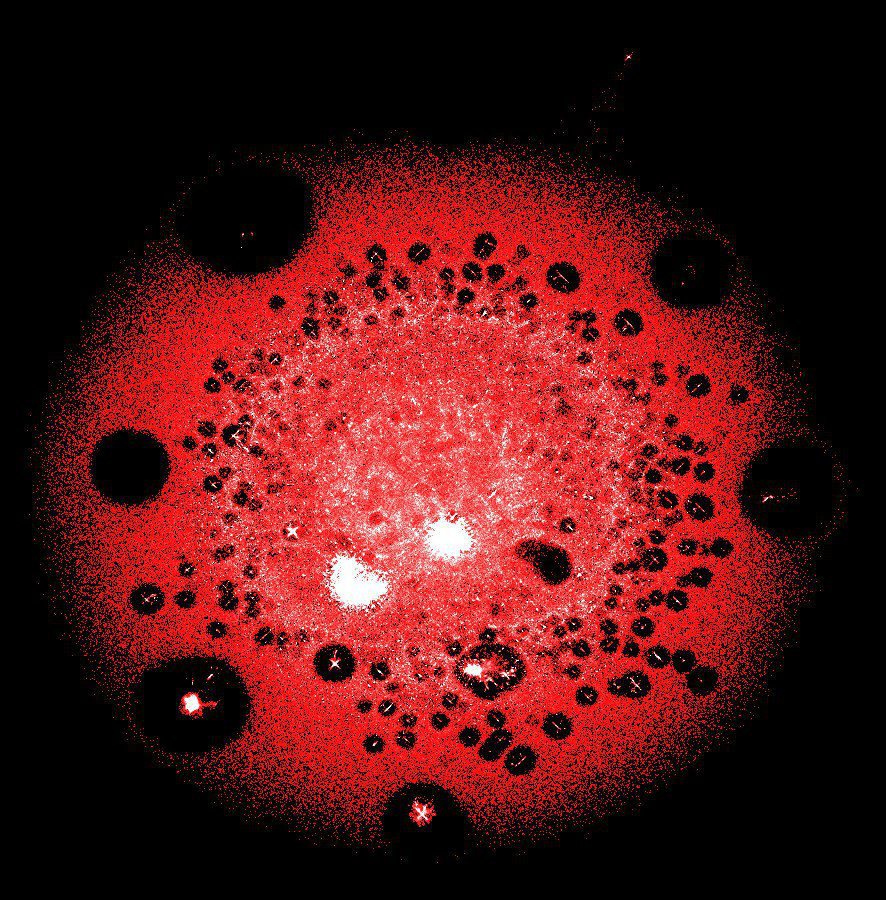
Plusieurs dizaines de millions de pics (transactions et adresses) dans l'un des plus grands clusters de blockchain Bitcoin
Un vrai salut lorsque vous devez dessiner un graphique géant. LargeViz fait référence aux algorithmes de réduction de dimensionnalité et peut être utilisé non seulement pour les graphiques, mais aussi pour les données tabulaires arbitraires. Il fonctionne à partir de la ligne de commande et offre d'excellentes performances. Très économique en mémoire et rapide.
Graphie

Adresses piratables en une semaine, et leurs transactions

Interface claire mais très limitée, paramètres par défaut raisonnables
Le seul outil commercial de cette liste. La graphie est un service qui prend vos données et effectue de lourds calculs de son côté. Le client regarde simplement la belle image dans le navigateur. En fait, gephi n'est pas mieux que les options par défaut et l'interactivité raisonnables. Il implémente un seul style: quelque chose de similaire à ForceAtlas. Il y a une limite de 800 000 pour le nombre maximum de sommets ou d'arêtes.
Intégrations de graphiques
Pour les tailles folles, il y a aussi une approche. Commençant déjà par un million de sommets, lors du dessin, il est logique de ne regarder que la densité des sommets à différents points de l'espace, simplement parce que rien d'autre ne peut être vu. La plupart des algorithmes inventés spécifiquement pour le rendu des graphiques fonctionneront pour des dizaines de millions de sommets ou d'arêtes pendant plusieurs heures, voire plusieurs jours. Vous pouvez sortir de cette situation en résolvant un problème légèrement différent. Il existe de nombreuses méthodes pour obtenir des représentations vectorielles d'une dimension donnée, reflétant les propriétés des sommets du graphique. Après avoir reçu de telles représentations, il ne reste plus qu'à réduire la dimension à 2 afin d'obtenir déjà l'image.
Node2Vec

Node2Vec + UMAP
Adaptation de word2vec standard pour les graphiques. Au lieu de séquences de mots, des séquences de sommets sont prises pour une traversée aléatoire du graphique et envoyées à word2vec au lieu de mots. La méthode ne prend en compte que les informations sur le voisinage des sommets. C'est généralement suffisant.
Verset
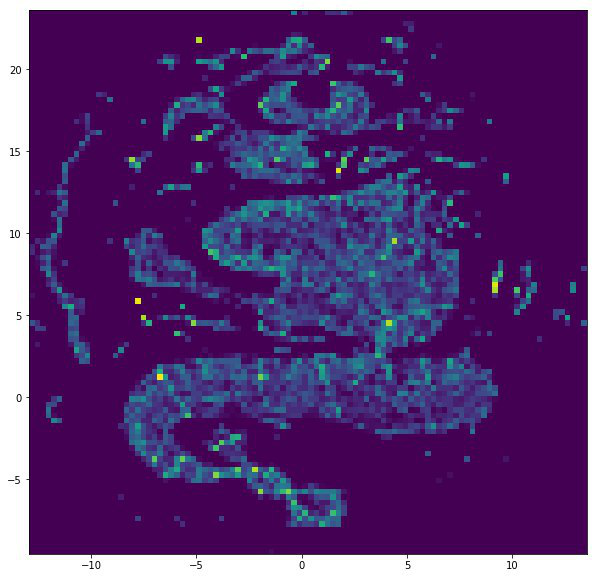
VERSE + UMAP
Un algorithme avancé pour obtenir des plongements de graphes, qui cherche à obtenir une représentation polyvalente pour les sommets, c'est-à-dire prendre en compte tous les rôles qu'un sommet joue dans un graphe. Le voisinage des sommets et la topologie locale du graphe sont pris en compte.
Graph convolutions

Graphique Convolutions + Autoencoder
Il existe de nombreuses façons de déterminer l’opération de convolution sur les graphiques, mais il s’agit essentiellement d’une «bavure» d’informations sur le graphique, de sorte que les sommets reçoivent des informations sur les signes de leurs voisins. Vous pouvez ajouter des informations de topologie locale à ces attributs.
Bonus: un peu plus sur la convolution graphique
Toutes les approches décrites sont basées sur des outils prêts à l'emploi. Ce dernier cas est une exception. Pour implémenter la convolution de graphe, vous devez réfléchir un peu et écrire un peu de code.
Une analyse détaillée des convolutions sur les graphiques et autres données non euclidiennes est un sujet digne d'un article séparé. Je décrirai ici l'approche de base la plus simple, qui ne nécessite pas de cadres graphiques spéciaux et est facilement évolutive. Nous voulons donc que les signes de chaque sommet du graphe contiennent des informations sur les signes des voisins.
Comment fait-on cela?
Le moyen le plus évident est de simplement prendre la moyenne des voisins. Si vous réfléchissez un peu plus à ce qui se passe et aux informations que la moyenne perd, vous pouvez y ajouter d'autres statistiques, telles que l'écart type, le minimum, le maximum, etc.
Comment l'organiser maintenant? Pour commencer, un graphe est essentiellement composé de nombreux sommets et de nombreux bords. Nous ne sommes intéressés que par les pièces connectées de plus d'un sommet, donc la liste des arêtes dans notre cas définit complètement le graphique. Ceci est commodément écrit sous la forme d'un tableau: dans la première colonne, les sommets d'où sort l'arête, dans la seconde, où ces arêtes entrent. Ensuite, nous devons lire les statistiques. C'est une tâche très courante et vous pouvez donc utiliser des frameworks dans lesquels tout est optimisé jusqu'à nous.
La puissance des frameworks de table dans l'analyse graphique
Nous sommes arrivés à la conclusion que nous avons une plaque spécifiant un graphique et que nous devons lire les statistiques pour certaines quantités. Tableaux et statistiques - tout cela est dans les pandas, donc ce qui suit sera un exemple de mise en œuvre.
Pour commencer, posons le graphe:
ara = np.arange(101).reshape(-1, 1) sample = np.vstack((np.hstack((ara[:-1], ara[1:])),
Il s'agit simplement d'une chaîne de 101 sommets connectés les uns après les autres, comme sur la figure.

Ensuite, nous définissons les signes des sommets au hasard:
feats = np.random.normal(size=(101, 10))
Et nous allons créer des cadres de données pandas à partir de tout cela:
edges = pd.DataFrame(sample, columns=['source', 'target']) cols = ['col{}'.format(i) for i in range(10)] feats = pd.DataFrame(feats, columns=cols) feats['target'] = ara
Maintenant, nous définissons la fonction de convolution elle-même:
def make_conv(edges, feats, cols, by, on, size=1000000, agg_f='mean', prefix='mean_'): """ edges -- edgelist: pandas dataframe with two columns (arguments by and on) feats -- features dataframe with key column (argument on) and features columns (argument cols) by -- column in edges to be used as source nodes on -- column in edges to be used as neighbor nodes size -- number of unique source nodes to be used in one chunk agg_f -- can be interpreted as pooling function. Pandas has several optimised functions for basic statistics, that can be passed as string arg (see pandas docs), but you also can provide any function you like prefix -- prefix for new column names """ res_feats = []
Que se passe-t-il ici
Tout d'abord, nous sélectionnons un morceau de sommets pour lequel nous allons faire une convolution, prendre toutes leurs arêtes, le concaténer avec les signes des voisins et l'écrire dans le bloc de données temporaire. Ensuite, nous regroupons par les sommets des sources, et agrégons en utilisant la fonction agg_f, qui est simplement moyenne par défaut. Ajoutez le résultat de la pièce actuelle à la liste et, à la fin, concaténez simplement les résultats.

Pour ce graphique, il ressemblera à ceci
Nous appliquons la fonction et dessinons le résultat:
conv1 = make_conv(edges, feats, cols, 'source', 'target') plt.figure(figsize=(3, 8)) plt.imshow(np.hstack((feats[cols].values, conv1.values[:, 1:])), cmap='jet');

Les signes initiaux, puis l'original et le résultat de la première convolution, puis l'original et le résultat de deux convolutions.
Par exemple, un cas si simple a été spécialement choisi qu'il était facile de voir visuellement comment les signes sont "maculés" chez les voisins si vous dessinez directement une matrice de signes. Dans un cas plus général, le processus ressemble à ceci:

Si vous voulez un peu plus de maths
Si vous avez déjà entendu parler des convolutions de graphes, c'était probablement dans le contexte des réseaux de convolution de graphes (Graph Convolutional Networks - GCN). Pour certains, les astuces avec les tablettes qui sont décrites ici peuvent sembler «pas difficiles». En fait, un article très intéressant est consacré à l'utilisation des convolutions de graphes sans apprentissage approfondi: «Simplifier les réseaux convolutionnels de graphes». Il donne une telle définition de la convolution
où
Est une matrice de fonctionnalités, et
Est le laplacien normalisé du graphique, qui est défini comme suit:
ici
La matrice d'adjacence du graphique est-elle additionnée à la matrice d'identité, et
- la matrice dans la diagonale dont les degrés des sommets du graphe sont enregistrés. Et tout cela est écrit en quelques lignes en python en utilisant scipy et numpy:
S = sparse.csgraph.laplacian(adj, normed=True) feats_conv = S @ feats
Ici, sparse est le module à l'intérieur de scipy pour travailler avec des matrices clairsemées, adj est la matrice d'adjacence, et feats et feats_conv sont les signes avant et après la convolution. Cette approche est plus rigoureuse, mais très mal mise à l'échelle. De plus, si vous pensez un peu à la signification de ce qui se passe, cela équivaut à la différence entre la valeur de l'entité au sommet et la moyenne dans les voisins du sommet, c'est-à-dire qu'elle peut être complètement résolue par le schéma précédent avec des tables, si vous ajoutez une opération.
Les références
Avis sur Visual Visualisationleonidzhukov.net/hse/2018/sna/papers/gibson2013arxiv.org/pdf/1710.04328.pdfSimplification des réseaux convolutionnels de graphesarxiv.org/pdf/1902.07153.pdfGraphVizgraphviz.orgGephigephi.orgigraphigraph.orgLargeVizarxiv.org/abs/1602.00370github.com/lferry007/LargeVisGraphiewww.graphistry.comNode2Vecsnap.stanford.edu/node2vecgithub.com/xgfs/node2vec-cVersettsitsul.in/publications/versegithub.com/xgfs/verseCahier avec code de package pandas completgithub.com/iggisv9t/graph-stuff/blob/master/Universal%20Convolver%20Example.ipynbGraph convolutionsVoici les travaux collectés sur les réseaux de convolution de graphes:
github.com/thunlp/GNNPapersL'essence de tout l'article dans un seul tableau