La représentation des limites (B-rep) est la principale méthode de représentation des objets modélisés dans la plupart des noyaux géométriques, y compris notre noyau C3D Modeler. Les algorithmes de base qui modifient les modèles, tels que l'application d'opérations de congé, l'exécution d'opérations de découpe et l'obtention de projections plates nécessitent la précision des représentations B-rep. La variété croissante de données 3D dans des formats polygonaux rend la tâche de transformations de modèles des polygones en représentation des limites de plus en plus pertinente. En conséquence, nous avons développé un nouveau SDK, C3D B-Shaper, qui fait partie de notre boîte à outils C3D.



L'utilisation d'un algorithme de triangulation (connu sous le nom de tessellation) sur la représentation des limites d'un modèle est relativement facile. La construction de représentations polygonales (pavées) est utile à des fins de visualisation et pour effectuer des calculs géométriques.

La transformation inverse - de la représentation polygonale à B-rep - fait cependant face à une série de problèmes liés à la complexité de reconnaître différents types de surfaces, y compris celles de forme libre. De plus, il y a le problème du bruit dans les modèles polygonaux qui apparaissent généralement à la suite du balayage 3D.

Le processus général par lequel C3D B-Shaper transforme les modèles des formats polygonaux en B-rep comprend trois étapes: la segmentation, la reconstruction des surfaces et la construction du modèle b-rep. Le processus de transformation est itératif: si les utilisateurs ne sont pas satisfaits des résultats pour quelque raison que ce soit, des corrections peuvent être apportées pendant les étapes de segmentation et de reconstruction de surface.


Transformer une représentation polygonale en B-rep

Cependant, avant d'amorcer le processus de transformation b-rep, nous améliorons la qualité du maillage polygonal source en appliquant les correctifs suivants: coordonner les directions des normales dans les polygones adjacents; éliminer les trous; et appliquer des algorithmes de lissage aux sources de maillage bruyantes, le cas échéant.

Segmentation du modèle polygonal

La première étape de la transformation consiste à segmenter le modèle polygonal. Nous classons le polygone maillé en sous-ensembles (segments). Les informations sur les normales à chaque sommet de maillage permettent d'effectuer une segmentation de premier ordre, puis d'effectuer le fractionnement initial du maillage, ainsi que de classer les zones comme plates ou fortement incurvées. Le fractionnement initial du maillage est basé sur la définition d'arêtes "nettes". Ce sont les arêtes entre deux polygones triangulaires où l'angle entre leurs normales moyennes dépasse une valeur prédéfinie.

Une segmentation de second ordre analyse le maillage en fonction de sa courbure principale, suffisante pour classer les surfaces élémentaires. Lors du calcul des courbures aux sommets du maillage, nous utilisons les résultats des travaux de Meyer (Mark Meyer, Mathieu Desbrun, Peter Schroder et Alan H. Barr, "Opérateurs de géométrie différentielle discrète pour les collecteurs triangulés à 2", Visualisation et mathématiques III, 2003) pour définir un opérateur différentiel discret pour des régions triangulées: un ensemble de sommets adjacents (liés à un sommet donné via une arête) est considéré pour chaque sommet de maillage initial. Ensuite, un opérateur discret K est calculé pour le sommet. En fonction de l'opérateur, les courbures moyennes normales, moyennes K _H et gaussiennes K _G sont définies au sommet du maillage.


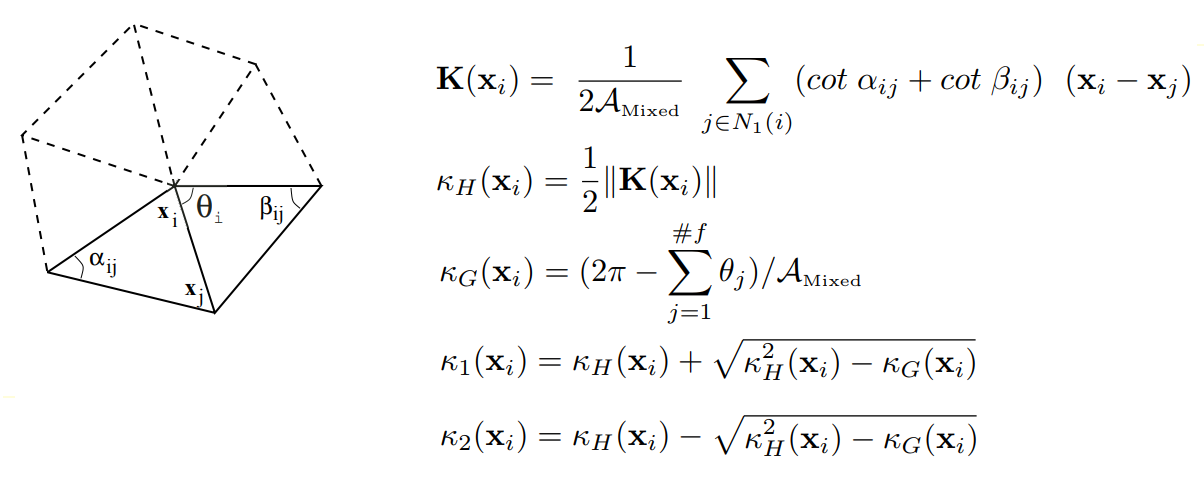Définition d'opérateurs différentiels discrets pour des régions triangulées

De cette manière, le tenseur de courbure est calculé pour chaque sommet de maillage, à partir duquel les valeurs de courbure principales K ₁ et K ₂ et les directions de courbure principales sont extraites.

Les sommets de maillage sont classés par les valeurs de leurs courbures principales K ₁ et K ₂ , puis sont calculés pour eux. L'algorithme de classification des sommets est basé sur k-moyennes, c'est-à-dire minimisant l'écart quadratique total des points d'amas par rapport aux centres des amas. La sortie résultante de l'algorithme contient un sommet de maillage associé à un cluster $$$Ci$et une paire de courbures (cluster-centre - L. Guillaume, «Segmentation de maillage triangulaire à tenseur de courbure avec rectification des limites», Actes Computer Graphics International (CGI), 2004).


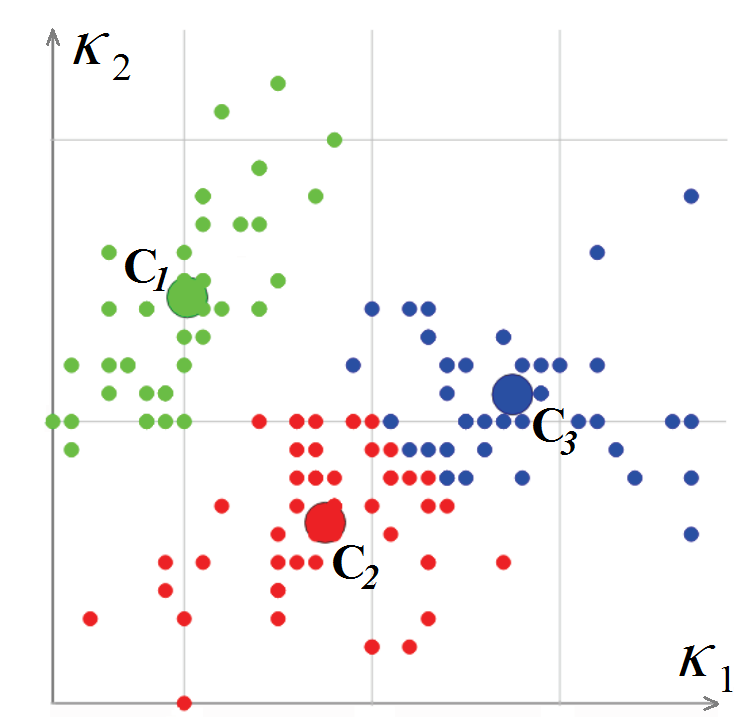Classification des sommets de maillage polygonaux dans l'espace de courbure

Une fois que nous avons fini de classer les sommets du maillage polygonal, nous continuons à classer les polygones. Pour commencer cette procédure, nous choisissons un polygone triangulaire dont la courbure peut être considérée comme entièrement définie. Il s'agit de celui dont les trois sommets sont dans un seul cluster, ou a deux sommets sur une arête vive. Le polygone est étiqueté comme un nouveau segment et devient le point de départ d'une procédure récursive qui étend le segment: pour chaque polygone triangulaire, les polygones adjacents sont considérés tant que le bord entre eux n'est pas "net". Lorsqu'un sommet de polygone adjacent, opposé à une arête commune, se trouve sur une arête vive ou appartient au même cluster, le polygone est ajouté au segment. Le processus est répété jusqu'à ce que tous les polygones composant le maillage aient disparu.


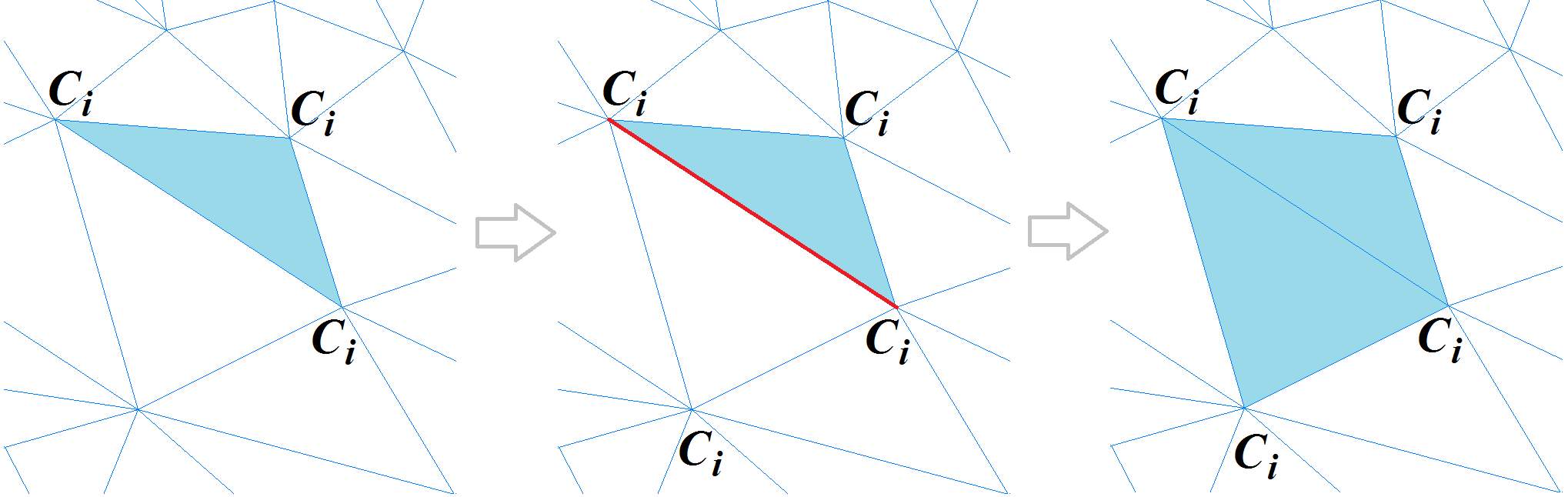Segmentation polygonale du maillage

Une fois la procédure de création de segment terminée, un autre algorithme assemble les segments adjacents pour éliminer la sur-segmentation du maillage.

Reconnaissance de type de surface

La deuxième étape est la reconnaissance de surface. Chaque segment doit être approximé par une surface avec une précision déterminée par le système ou par les utilisateurs.

Tout d'abord, les valeurs de courbure principales des segments sont utilisées pour déterminer s'il est possible de décrire la forme du segment par l'une des surfaces élémentaires suivantes:

• Plan: k ₁ = k ₂ = 0
• Sphère: k ₁ = k ₂ = K > 0
• Cylindre: k ₁ = K > 0, k ₂ = 0
• Cône: k ₁ ∈ [ a , b ], k ₂ = 0
• Toroïde: k ₁ = K , k ₂ ∈ [ a , b ]

Pour créer des surfaces élémentaires, nous ajustons des objets géométriques simples sur des ensembles de points en utilisant l'algorithme approprié. Par exemple, pour ajuster un cercle et une sphère sur un ensemble de points, la méthode des moindres carrés est utilisée; pour ajuster un plan, l'analyse en composantes principales est utilisée. Le système garantit que chaque surface reconstruite est liée à un segment dans une précision de reconnaissance prédéfinie.

La figure ci-dessous illustre les surfaces reconnues par couleur: les plans sont affichés en bleu, les cylindres sont en rouge, les sphères en vert, les cônes jaunes et les tores violets.


Maillage polygonal source (gauche) et maillage segmenté (droite) avec des segments de surface reconnus

Si aucune surface élémentaire n'est capable de décrire le segment, alors le système tente de reconnaître une surface d'extrusion ou une surface de révolution.

Lorsque le système ne parvient finalement pas à trouver une surface analytique permettant de décrire la forme du segment, une surface NURBS est créée pour elle.

Création de modèle B-rep

La dernière étape de la transformation consiste à créer le modèle B-rep basé sur la segmentation et les données de surface reconstruites. Un graphe d'adjacence est créé à partir des régions segmentées pour représenter la topologie du modèle et constitue la base de la création du modèle B-rep résultant. Les modèles B-rep sont assemblés en mode entièrement automatique, contrairement aux étapes précédentes:

• Les arêtes B-rep sont créées à partir de courbes d'intersection de surfaces reconstruites adjacentes
• Les faces B-rep sont construites par des surfaces reconnues bornées et des arêtes B-rep

Il n'est cependant pas toujours possible de créer un shell avec la topologie correcte. Par exemple, prenez deux surfaces telles qu'un cylindre et un plan qui sont presque tangentes l'une à l'autre dans l'espace. En raison de la tolérance spécifiée pour les surfaces reconstruites, elles peuvent ne pas se croiser du tout. Par conséquent, le shell créé peut présenter des défauts. Les utilisateurs peuvent éliminer les défauts en corrigeant les paramètres de surface.

Types de modèles polygonaux

Il existe de nombreuses sources de modèles polygonaux disponibles en ligne:

• Les catalogues et bases de données en ligne proposent des modèles 3D aux formats polygonaux comme STL, VRML et OBJ de 3D Warehouse, Cults 3D, etc.
• Fichiers résultant de la numérisation 3D
• Sortie de l'optimisation topologique des modèles à l'aide d'algorithmes CAE

Les modèles polygonaux de ces sources peuvent être divisés en deux groupes: les modèles triangulés (maillés) à partir d'objets B-rep et tous les autres modèles. Une paire de caractéristiques spécifiques au premier groupe est l'absence de bruit de maillage polygonal et la domination des surfaces analytiques. Cela signifie que les modèles du premier groupe peuvent être facilement transformés en b-reps en mode entièrement automatisé ou avec un effort minimal de l'utilisateur.

Les maillages polygonaux des modèles du deuxième groupe ont du bruit, contiennent des surfaces organiques et sont donc plus susceptibles de nécessiter la participation interactive des utilisateurs.

Ainsi, nous proposons deux modes de fonctionnement C3D B-Shape, entièrement automatiques et interactifs. Les utilisateurs peuvent basculer entre les modes de reconnaissance et gérer les types de surfaces pendant le processus de reconstruction. La sélection d'un mode peut dépendre de l'objectif de la transformation: les utilisateurs peuvent parfois vouloir ignorer la connectivité topologique du shell résultant, ou son exactitude globale. C'est souvent le cas lors de l'optimisation de l'affichage dans les applications BIM, dans lesquelles les utilisateurs ajoutent des éléments intérieurs personnalisés au modèle architectural.

D'un autre côté, les tâches d'ingénierie inverse nécessitent la copie la plus précise possible des modèles source afin que le modèle résultant ait une topologie correcte. Il est donc nécessaire de prédéfinir la précision, disons, de la co-axialité des cylindres ou de la tangence de deux surfaces. Dans ce type de cas, la participation des utilisateurs au processus de transformation est cruciale.

La transformation automatique du C3D B-Shaper utilise les fonctions suivantes qui utilisent comme données d'entrée le maillage source et les paramètres de transformation:

MbResultType ConvertMeshToShell( MbMesh & mesh, MbFaceShell *& shell, const MbMeshProcessorValues & params ); MbResultType ConvertCollectionToShell( MbCollection & collection, MbFaceShell *& shell, const MbMeshProcessorValues & params ); 

L'un des paramètres de transformation est une valeur de précision de reconnaissance qui définit la tolérance maximale pour les distances entre les sommets des segments et les surfaces reconnues. La précision peut être absolue ou relative. Lorsque vous utilisez la précision relative, les écarts des faces par rapport aux corps maillés sont mesurés par rapport à la taille du modèle.

La classe d'interface du processeur MbMesh offre des options avancées pour gérer la segmentation et la reconnaissance des surfaces:

 class MbMeshProcessor { .. public: // Mesh rectification. void SetUseMeshSmoothing( bool useSmoothing ); // Mesh segmentation management. const MbCollection & GetSegmentedMesh(); MbResultType SegmentMesh( bool createSurfaces = true ); void ResetSegmentation(); void UniteSegments( size_t firstSegmentIdx, size_t secondSegmentIdx ); MbResultType SegmentMeshBySeparators( const std::vector<std::vector<uint>> & sep ); // Surface recognition management. void FitSurfaceToSegment( size_t idxSegment ); void FitSurfaceToSegment( size_t idxSegment, MbeSpaceType surfaceType ); const MbSurface * GetSegmentSurface( size_t idxSegment ) const; // B-rep shell construction. MbResultType CreateBRepShell( MbFaceShell *& pShell ); .. } 

Pour, par exemple, corriger les résultats de la segmentation automatique, C3D B-Shaper propose des outils pour fusionner et diviser des segments, etc. Les utilisateurs peuvent ajuster des surfaces de types donnés sur le segment sélectionné, ainsi que modifier les paramètres des surfaces reconnues.

Résumé

Le résultat des algorithmes de transformation de C3D B-Shaper est illustré par les figures ci-dessous, dans lesquelles un modèle 3D complexe est transformé avec succès de sa représentation maillée polygonale en un solide de représentation de frontière.




Maillage polygonal (à gauche) et modèle B-rep (à droite) convertis avec C3D B-Shaper

Notre objectif est de créer un puissant SDK pour transformer les modèles de polygonaux en B-rep, et le développement du C3D B-Shaper se poursuit donc. Nous travaillons notamment à faire progresser les algorithmes de segmentation automatique, à développer des outils d'édition de segmentation, à améliorer la construction de surfaces NURBS de forme libre et à améliorer la qualité des assemblages de shell B-rep.

Les clients qui utilisent le noyau géométrique C3D jouent également un rôle moteur dans le développement du C3D B-Shaper.

Les développeurs sont invités à tester C3D B-Shaper dans le cadre de la boîte à outils C3D ou en tant que composant autonome.

Par Andrey Tumanin, responsable du développement logiciel chez C3D Labs