Calcul de l'hypothèse nulle, par exemple, l'analyse des salaires des programmeurs ukrainiens

J'ai décidé de le partager, mais je n'oublierais pas moi-même comment de simples outils statistiques peuvent être utilisés pour analyser les données. Une enquête anonyme a été utilisée comme exemple concernant les salaires, l'ancienneté et les postes des programmeurs ukrainiens pour 2014 et 2019. (1)

Étapes d'analyse

• Prétraitement des données et analyse préliminaire ( toute personne intéressée par le code ici )
• Une représentation graphique des données. Fonction de densité de distribution.
• Nous formulons l'hypothèse nulle (H0) (2)
• Choisissez une métrique pour l'analyse
• Nous utilisons la méthode d'amorçage pour former un nouveau tableau de données.
• Nous calculons la valeur de p (3) pour confirmer ou réfuter l'hypothèse

Prétraitement des données

Après quelques manipulations (le code est ici ), nous présentons les données sous la forme suivante:

#      ,  . display(data_14_1.head(), data_19_1.head()) print('  : \n \ {} .  14   {}  19 '.format(len(data_14_1), len(data_19_1))) 

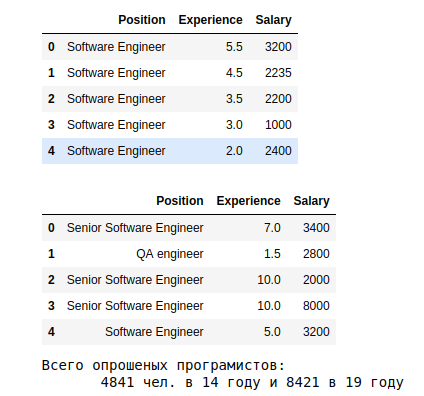
Un peu plus de regroupements pendant un an (soit le 19):

 # ,  19  display(pd.DataFrame(df.groupby(['Experience'])['Salary'].mean().sort_values(ascending=False)), \ pd.DataFrame(df.groupby(['Position'])['Salary'].mean().sort_values(ascending=False)), \ df.Position.value_counts()) 

Les premières estimations sont les suivantes.

a. Les résultats montrent qu'en moyenne sur 19, ceux qui travaillent depuis plus de 10 ans reçoivent plus de 3,5k. La dépendance de l'expérience -> zp

c. Moyenne s.p. en 19, selon la spécialisation, ils affichent un écart de 10 fois - de 5k pour System Architect, à 575 pour Junior QA.

s La dernière planche montre la répartition par profession. La plupart des données sur l'ingénieur logiciel, sans qualification.

Nous attirons l'attention sur les caractéristiques de la 19e année: quelque chose ne va pas avec la 9e année d'expérience et il n'y a pas de classement selon les niveaux de junior, moyen, senior. Vous pouvez mieux comprendre les raisons de la valeur aberrante de la 9e année. Mais pour cette analyse, nous le prenons tel quel.

Mais avec les catégories - ça vaut le coup de régler. en 19 ans, l'ingénieur logiciel 2739 personnes (35% de tous) sans indiquer le niveau de qualification. Calculons la moyenne et les écarts pour ceux qui ont indiqué.



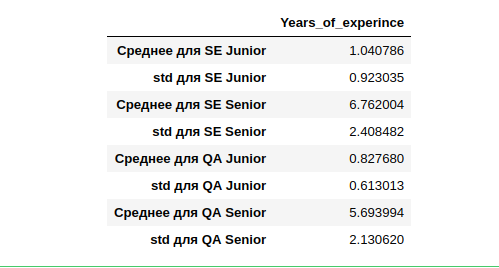
Il s'avère que l'expérience de travail moyenne (qui l'a indiqué) pour SE Junior est d'un an, avec un écart assez large d'un an. SE Senior a le plus d'expérience avec un écart de 2,4 ans tout aussi important.

Si nous essayons de calculer Middle et d'utiliser l'expérience moyenne de ceux qui l'ont indiqué, puis de catégoriser celui qui ne l'a pas indiqué, nous pouvons ne pas regrouper correctement l'échantillon entier. Nous ferons surtout des erreurs sur d'autres spécialités (pas SE et QA) c'est à dire trop peu de données. De plus, ils sont peu nombreux à comparer à la 14e année.

Que puis-je utiliser d'autre?

Prenons uniquement le niveau de salaire comme indicateur fiable du niveau de compétence! (Je pense qu'il y aura dissidence).

Tout d'abord, nous construisons à quoi ressemble la distribution des salaires pour la 19e année.





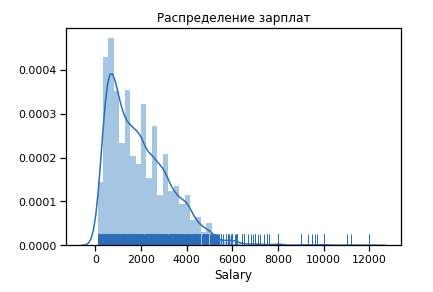
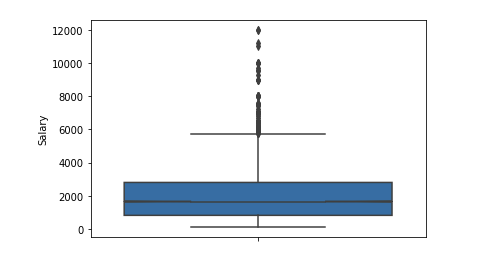
Valeurs aberrantes en nombre significatif après 6 k $. Nous quittons la plage de limitations [400 - 4000]. Tout programmeur devrait en obtenir plus de 400 :)

 df_new = data_19_1[(data_19_1['Salary'] > 400) & (data_19_1['Salary'] < 4000)] sns.distplot(df_new['Salary'], rug=True, norm_hist=True) 

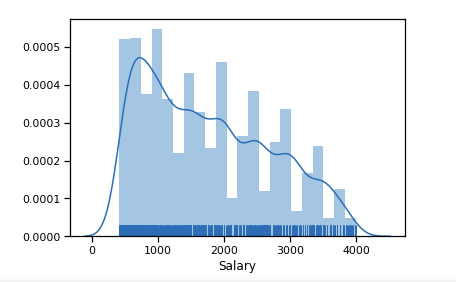
Déjà un peu plus proche de la distribution normale.

Nous composons depuis 19 ans, les niveaux de compétence en fonction de la DP. La gamme de 3600 $ nous donne un bon diviseur en 3 catégories - 1200 $

 df_new.reset_index() df_new.loc['level'] = 0 df_new.loc[df_new.Salary <= 1200, 'level'] = 'Junior' df_new.loc[(df_new.Salary > 1200) & (df_new.Salary <= 2400), 'level'] = 'Middle' df_new.loc[df_new.Salary > 2401, 'level'] = 'Senior' 

Tirage - densité de catégorie depuis 19 ans.

 sns.set(style="whitegrid") fig, ax = plt.subplots() fig.set_size_inches(11.7, 8.27) plt.title('      19 ') sns.barplot(x='level', y='Salary', hue='Experience', hue_order=[1,3,5,7,10], palette='Blues', \ data=df_new, ci='sd') 

En ajoutant la quantité d'expérience spécifiée (coin gauche), vous pouvez voir différentes nuances. Par exemple, que Junior gagne en moyenne jusqu'à 1k et son expérience de travail est de 5 ans. La plus grande dispersion de sn chez Senior (une courte ligne noire en haut de chaque colonne) et bien d'autres détails intéressants.

C'est là que les deux premières étapes sont terminées, nous procédons au test d'hypothèses par bootstraping.

Nous formulons l'hypothèse nulle (H0)

Lors des premières étapes, nous avons découvert que l'expérience de travail spécifiée ne signifie pas très précisément le niveau de qualification. Ensuite, nous formons l'hypothèse nulle (celle qui doit être réfutée)

Il existe de nombreuses options (par exemple):

• La dépendance du salaire à l'ancienneté dans l'année 14 est la même que dans la 19e.
• Les salaires des juniors n'ont pas changé depuis 14 ans.

Cependant, comme l'expérience indiquée est un mauvais indicateur et que le calcul pour certaines catégories peut prêter à confusion, nous prenons une option simple et plus substantielle: le niveau moyen de sn à 14, le même qu'en 19, est notre hypothèse nulle H0 (2).

Autrement dit, nous supposons que les salaires pendant 5 ans n'ont pas changé.

PAS la fidélité de l'hypothèse, malgré toute son évidence, nous pouvons vérifier avec précision en calculant la valeur P pour l'hypothèse nulle.

 #       (14  19 ),    95 % mean_salary_14 = np.mean(data_14_1['Salary']) conf_salary_14 = np.percentile(data_14_1['Salary'], [2.5, 97.5]) mean_salary_19 = np.mean(data_19_1['Salary']) conf_salary_19 = np.percentile(data_19_1['Salary'], [2.5, 97.5]) diff_mean_salary = mean_salary_19 - mean_salary_14 

Le salaire moyen de l'année 14 est de 1797 $, où l'intervalle de confiance est de 95% [300,0 4000,0]
Le salaire moyen en 19 ans est de 1949 $, où l'intervalle de confiance est de 95% [300,0 5000,0]

La différence de salaire moyen entre les années 14 et 19: 152 $

Métrique pour l'analyse

Il est logique de choisir les valeurs moyennes comme métrique. D'autres options sont possibles, par exemple la médiane, qui se fait souvent dans le cas d'un nombre important de valeurs aberrantes. Cependant, la moyenne en tant qu'estimation est facile à comprendre et donne également une bonne idée.

Écriture d'une fonction d'amorçage.

 #   bootstraping def bootstrap(data, func): boots = np.random.choice(data, len(data)) return func(boots) def bootstrapping(data, func=np.mean, size=1): reps = np.empty(size) for i in range(size): reps[i] = bootstrap(data, func) return reps 

Nous calculons nos statistiques.

 #  14  19   -       data = np.concatenate((data_14_1['Salary'].values, data_19_1['Salary'].values)) #     2  data_mean = np.mean(data) #      14  19 ,           data_14_shifted = data_14_1['Salary'].values - np.mean(data_14_1['Salary'].values) + data_mean data_19_shifted = data_19_1['Salary'].values - np.mean(data_19_1['Salary'].values) + data_mean #  10000     ,   data_14_bootsted = bootstrapping(data_14_shifted, np.mean, size=10000) data_19_bootsted = bootstrapping(data_19_shifted, np.mean, size=10000) #       .      . mean_diff = data_19_bootsted - data_14_bootsted #  P value               . p_value = sum(mean_diff >= diff_mean_salary) / len(mean_diff) print('p-value = {}'.format(p_value)) 

valeur p = 0,0

Les valeurs P jusqu'à 0,05 sont considérées comme insignifiantes, et dans notre cas, elles sont égales à 0. Ce qui signifie que l'hypothèse nulle est réfutée - le salaire moyen des années 14 et 19 est différent et ce n'est pas un résultat accidentel ou un nombre significatif de valeurs aberrantes.

Nous avons généré 10 000 de ces tableaux, en moyenne, ne pouvaient pas obtenir un total de plus de détachements de ce type que les données elles-mêmes.

Bien que nous ayons consacré beaucoup d'attention aux deux premières étapes, nous avons formulé l'hypothèse correcte et choisi la bonne métrique. Dans des tâches plus complexes, avec un grand nombre de variables, sans de telles étapes préliminaires, l'analyse peut conduire à une interprétation incorrecte. Ne les sautez pas.

À la suite de notre étude du niveau des salaires pendant 14 et 19 ans, nous sommes parvenus aux conclusions suivantes:

1. Sur la base des données de l'enquête, l'expérience spécifiée n'est pas un critère tout à fait approprié pour déterminer le niveau des salaires et des qualifications.
2. La division en niveau de compétence sera très probablement basée sur le niveau des salaires.
3. Les salaires des programmeurs sont passés de 14 à 19 (en moyenne 8,5%) et ce n'est pas un résultat accidentel.

Merci de votre attention. Je serai ravi des commentaires et des critiques.

Les sources

1. https://jobs.dou.ua/salaries/ (résultats de l'enquête)
2. https://en.wikipedia.org/wiki/Null_hypothesis
3. https://en.wikipedia.org/wiki/P-value