Aujourd'hui, je voudrais parler du déballage des listes imbriquées de profondeur indéfinie. Ceci est une tâche assez non triviale, donc je voudrais parler ici de ce que sont les implémentations, de leurs avantages et inconvénients et d'une comparaison de leurs performances.

L'article comprendra plusieurs sections ci-dessous:

Les fonctions
Les données
Résultats
Conclusions

Partie 1. Fonctions

Implémentations empruntées

externe_flatten_1

Implémentation

def outer_flatten_1(array: Iterable) -> List: """ Based on C realization of this solution More on: https://iteration-utilities.readthedocs.io/en/latest/generated/deepflatten.html https://github.com/MSeifert04/iteration_utilities/blob/384948b4e82e41de47fa79fb73efc56c08549b01/src/deepflatten.c """ return deepflatten(array)

J'ai pris cette fonction pour analyser à partir d'un package externe, iteration_utilities.

L'implémentation a été effectuée en C, laissant à python une interface d'appel de fonction de haut niveau.
L'implémentation de la fonction en C est assez lourde, vous pouvez la voir en cliquant sur le lien dans le spoiler. La fonction est un itérateur.

 >>> from typing import Iterator, Generator >>> from iteration_utilities import deepflatten >>> isinstance(deepflatten(a), Iterator) True >>> isinstance(deepflatten(a), Generator) False

Il est difficile de dire sur la complexité de l'algorithme implémenté ici, je laisse donc cet intérêt aux utilisateurs Habr.

En général, je voudrais également noter que toutes les autres fonctions de cette bibliothèque sont assez rapides et sont également implémentées en C.

external_flatten_2

Implémentation

 def outer_flatten_2(array: Iterable) -> List: """ recursive algorithm, vaguely reminiscent of recursion_flatten. Based on next pattern: .. code:: python try: tree = iter(node) except TypeError: yield node more on: https://more-itertools.readthedocs.io/en/stable/api.html#more_itertools.collapse """ return collapse(array)

L'implémentation de cette méthode de décompression des listes imbriquées est également dans le package externe, à savoir more_itertools.
La fonction est effectuée sur du python pur, mais pas optimal, à mon avis. Une implémentation détaillée peut être vue dans le lien de la documentation.
La complexité de cet algorithme est O (n * m).

Implémentations propres

niccolum_flatten

Implémentation

 def niccolum_flatten(array: Iterable) -> List: """ Non recursive algorithm Based on pop/insert elements in current list """ new_array = array[:] ind = 0 while True: try: while isinstance(new_array[ind], list): item = new_array.pop(ind) for inner_item in reversed(item): new_array.insert(ind, inner_item) ind += 1 except IndexError: break return new_array

Quand il est apparu d'une manière ou d'une autre dans des télégrammes au public @ru_python_beginners sur la mise en œuvre du déballage des listes imbriquées d'imbrication indéfinie, j'ai proposé ma propre option.

Cela consiste dans le fait que nous copions la liste d'origine (afin de ne pas la modifier), puis dans la boucle while True, nous vérifions que l'élément est une liste - nous la parcourons et insérons le résultat au tout début.

Oui, maintenant je comprends que cela ne semble pas optimal et difficile, car la réindexation se produit à chaque fois (parce que nous ajoutons et supprimons en haut de la liste), mais cette option a également le droit à la vie et nous vérifierons son implémentation avec le reste.

La complexité de cet algorithme est O (n ^ 3 * m) en raison de la reconstruction de la liste deux fois pour chaque itération passée

tishka_flatten

Implémentation

 def tishka_flatten(data: Iterable) -> List: """ Non recursive algorithm Based on append/extend elements to new list """ nested = True while nested: new = [] nested = False for i in data: if isinstance(i, list): new.extend(i) nested = True else: new.append(i) data = new return data

L'un des premiers a également montré la mise en œuvre de Tishka17 . Cela consiste dans le fait qu'à l'intérieur de la boucle while imbriquée itère sur la liste existante avec la clé nested = False, et si elle a au moins une fois obtenu une feuille, elle quitte le drapeau nested = True et étend cette feuille à la liste. En conséquence, il s'avère que pour chaque cycle, il établit un niveau d'imbrication, combien de niveaux d'imbrication il y aura - il y aura tellement de passages à travers le cycle. Comme on peut le voir dans la description - pas l'algorithme le plus optimal, mais quand même, il est différent du reste.
La complexité de cet algorithme est O (n * m).

zart_flatten

Implémentation

 def zart_flatten(a: Iterable) -> List: """ Non recursive algorithm Based on pop from old and append elements to new list """ queue, out = [a], [] while queue: elem = queue.pop(-1) if isinstance(elem, list): queue.extend(elem) else: out.append(elem) return out[::-1]

Un algorithme également suggéré par l'un des participants au chat expérimenté. À mon avis, c'est assez simple et propre. Sa signification est que si l'élément est une liste, nous ajoutons le résultat à la fin de la liste d'origine, et sinon, nous l'ajoutons à la sortie. Je l'appellerai ci-dessous le mécanisme d'extension / ajout. En conséquence, nous affichons la liste plate résultante résultante inversée afin de conserver l'ordre d'origine des éléments.

La complexité de cet algorithme est O (n * m).

recursive_flatten_iterator

Implémentation

 def recursive_flatten_iterator(arr: Iterable) -> Iterator: """ Recursive algorithm based on iterator Usual solution to this problem """ for i in arr: if isinstance(i, list): yield from recursion_flatten(i) else: yield i

La solution la plus courante à ce problème est probablement la récursivité et le rendement à partir de. Peu de choses peuvent être dites - l'algorithme semble assez simple et efficace, à part le fait qu'il se fait par récursivité et, avec de grandes enceintes, il peut y avoir une pile d'appels assez importante.

La complexité de cet algorithme est O (n * m).

recursive_flatten_generator

Implémentation

 def recursive_flatten_generator(array: Iterable) -> List: """ Recursive algorithm Looks like recursive_flatten_iterator, but with extend/append """ lst = [] for i in array: if isinstance(i, list): lst.extend(recursive_flatten_list(i)) else: lst.append(i) return lst

Cette fonction est assez similaire à la précédente, elle n'est exécutée que via un itérateur, mais via un mécanisme d'extension / ajout récursif.

La complexité de cet algorithme est O (n * m).

tishka_flatten_with_stack

Implémentation

 def tishka_flatten_with_stack(seq: Iterable) -> List: """ Non recursive algorithm Based on zart_flatten, but build on try/except pattern """ stack = [iter(seq)] new = [] while stack: i = stack.pop() try: while True: data = next(i) if isinstance(data, list): stack.append(i) i = iter(data) else: new.append(data) except StopIteration: pass return new

Un autre algorithme que Tishka a fourni, qui, en fait, est très similaire à zart_flatten, cependant, il a été implémenté via un simple mécanisme d'extension / ajout, puis par itération dans une boucle infinie dans laquelle ce mécanisme est utilisé. Ainsi, il s'est avéré quelque chose de similaire à zart_flatten, mais par itération et tout en True.

La complexité de cet algorithme est O (n * m).

Partie 2. Données

Pour tester l'efficacité de ces algorithmes, nous devons créer des fonctions pour la génération automatique de listes d'une certaine imbrication, que j'ai traitées avec succès et vous montrerons le résultat ci-dessous:

create_data_decreasing_depth

Implémentation

 def create_data_decreasing_depth( data: Union[List, Iterator], length: int, max_depth: int, _current_depth: int = None, _result: List = None ) -> List: """ creates data in depth on decreasing. Examples: >>> data = create_data_decreasing_depth(list(range(1, 11)), length=5, max_depth=3) >>> assert data == [[[1, 2, 3, 4, 5], 6, 7, 8, 9, 10]] >>> data = create_data_decreasing_depth(list(range(1, 11)), length=2, max_depth=3) >>> assert data == [[[1, 2], 3, 4], 5, 6], [[7, 8,] 9, 10]] """ _result = _result or [] _current_depth = _current_depth or max_depth data = iter(data) if _current_depth - 1: _result.append(create_data_decreasing_depth( data=data, length=length, max_depth=max_depth, _current_depth=_current_depth - 1, _result=_result)) try: _current_length = length while _current_length: item = next(data) _result.append(item) _current_length -= 1 if max_depth == _current_depth: _result += create_data_decreasing_depth( data=data, length=length, max_depth=max_depth) return _result except StopIteration: return _result

Cette fonction crée des listes imbriquées avec une imbrication décroissante.

  >>> data = create_data_decreasing_depth(list(range(1, 11)), length=5, max_depth=3) >>> assert data == [[[1, 2, 3, 4, 5], 6, 7, 8, 9, 10]] >>> data = create_data_decreasing_depth(list(range(1, 11)), length=2, max_depth=3) >>> assert data == [[[1, 2], 3, 4], 5, 6], [[7, 8,] 9, 10]]

create_data_increasing_depth

Implémentation

 def create_data_increasing_depth( data: Union[List, Iterator], length: int, max_depth: int, _current_depth: int = None, _result: List = None ) -> List: """ creates data in depth to increase. Examples: >>> data = create_data_increasing_depth(list(range(1, 11)), length=5, max_depth=3) >>> assert data == [1, 2, 3, 4, 5, [6, 7, 8, 9, 10]] >>> data = create_data_increasing_depth(list(range(1, 11)), length=2, max_depth=3) >>> assert data == [1, 2, [3, 4, [5, 6]]], 7, 8, [9, 10]] """ _result = _result or [] _current_depth = _current_depth or max_depth data = iter(data) try: _current_length = length while _current_length: item = next(data) _result.append(item) _current_length -= 1 except StopIteration: return _result if _current_depth - 1: tmp_res = create_data_increasing_depth( data=data, length=length, max_depth=max_depth, _current_depth=_current_depth - 1) if tmp_res: _result.append(tmp_res) if max_depth == _current_depth: tmp_res = create_data_increasing_depth( data=data, length=length, max_depth=max_depth) if tmp_res: _result += tmp_res return _result

Cette fonction crée des listes imbriquées avec une imbrication croissante.

  >>> data = create_data_increasing_depth(list(range(1, 11)), length=5, max_depth=3) >>> assert data == [1, 2, 3, 4, 5, [6, 7, 8, 9, 10]] >>> data = create_data_increasing_depth(list(range(1, 11)), length=2, max_depth=3) >>> assert data == [1, 2, [3, 4, [5, 6]]], 7, 8, [9, 10]]

generate_data

Implémentation

 def generate_data() -> List[Tuple[str, Dict[str, Union[range, Num]]]]: """ Generated collections of Data by pattern {amount_item}_amount_{length}_length_{max_depth}_max_depth where: .. py:attribute:: amount_item: len of flatten elements .. py:attribute:: length: len of elements at the same level of nesting .. py:attribute:: max_depth: highest possible level of nesting """ data = [] amount_of_elements = [10 ** i for i in range(5)] data_template = '{amount_item}_amount_{length}_length_{max_depth}_max_depth' # amount_item doesn't need to be [1] for amount_item in amount_of_elements[1:]: for max_depth in amount_of_elements: # for exclude flatten list after generate data by create_data_increasing_depth if amount_item > max_depth: # generate four types of length for length in range(0, max_depth + 1, math.ceil(max_depth / 4)): # min length must be 1 length = length or 1 data_name = data_template.format( amount_item=amount_item, length=length, max_depth=max_depth ) data_value = { 'data': range(amount_item), 'length': length, 'max_depth': max_depth } data.append((data_name, data_value)) # for not to produce more than 1 flat entity if max_depth == 1: break # this order is convenient for me data = sorted(data, key=lambda x: [x[1]['data'][-1], x[1]['max_depth'], x[1]['length']]) return data

Cette fonction crée directement des modèles pour les données de test. Pour ce faire, il génère des en-têtes créés par le modèle.

 data_template = '{amount_item}_amount_{length}_length_{max_depth}_max_depth'

Où:

montant - le nombre total d'articles dans la liste
longueur - le nombre d'éléments à un niveau d'imbrication
max_depth - nombre maximum de niveaux d'imbrication

Les données elles-mêmes sont transférées aux fonctions ci-dessus pour générer les données nécessaires. En conséquence, la sortie, comme nous le verrons plus tard, nous aurons les données suivantes (en-têtes):

 10_amount_1_length_1_max_depth 100_amount_1_length_1_max_depth 100_amount_1_length_10_max_depth 100_amount_3_length_10_max_depth 100_amount_6_length_10_max_depth 100_amount_9_length_10_max_depth 1000_amount_1_length_1_max_depth 1000_amount_1_length_10_max_depth 1000_amount_3_length_10_max_depth 1000_amount_6_length_10_max_depth 1000_amount_9_length_10_max_depth 1000_amount_1_length_100_max_depth 1000_amount_25_length_100_max_depth 1000_amount_50_length_100_max_depth 1000_amount_75_length_100_max_depth 1000_amount_100_length_100_max_depth 10000_amount_1_length_1_max_depth 10000_amount_1_length_10_max_depth 10000_amount_3_length_10_max_depth 10000_amount_6_length_10_max_depth 10000_amount_9_length_10_max_depth 10000_amount_1_length_100_max_depth 10000_amount_25_length_100_max_depth 10000_amount_50_length_100_max_depth 10000_amount_75_length_100_max_depth 10000_amount_100_length_100_max_depth 10000_amount_1_length_1000_max_depth 10000_amount_250_length_1000_max_depth 10000_amount_500_length_1000_max_depth 10000_amount_750_length_1000_max_depth 10000_amount_1000_length_1000_max_depth

Partie 3. Résultats

Pour profiler le CPU - j'ai utilisé line_profiler
Pour la représentation graphique - timeit + matplotlib

CPU Profiler

Conclusion

 $ kernprof -l funcs.py $ python -m line_profiler funcs.py.lprof Timer unit: 1e-06 s Total time: 1.7e-05 s File: funcs.py Function: outer_flatten_1 at line 11 Line # Hits Time Per Hit % Time Line Contents ============================================================== 11 @profile 12 def outer_flatten_1(array: Iterable) -> List: 13 """ 14 Based on C realization of this solution 15 More on: 16 17 https://iteration-utilities.readthedocs.io/en/latest/generated/deepflatten.html 18 19 https://github.com/MSeifert04/iteration_utilities/blob/384948b4e82e41de47fa79fb73efc56c08549b01/src/deepflatten.c 20 """ 21 2 17.0 8.5 100.0 return deepflatten(array) Total time: 3.3e-05 s File: funcs.py Function: outer_flatten_2 at line 24 Line # Hits Time Per Hit % Time Line Contents ============================================================== 24 @profile 25 def outer_flatten_2(array: Iterable) -> List: 26 """ 27 recursive algorithm, vaguely reminiscent of recursion_flatten. Based on next pattern: 28 29 .. code:: python 30 31 try: 32 tree = iter(node) 33 except TypeError: 34 yield node 35 36 more on: 37 https://more-itertools.readthedocs.io/en/stable/api.html#more_itertools.collapse 38 """ 39 2 33.0 16.5 100.0 return collapse(array) Total time: 0.105099 s File: funcs.py Function: niccolum_flatten at line 42 Line # Hits Time Per Hit % Time Line Contents ============================================================== 42 @profile 43 def niccolum_flatten(array: Iterable) -> List: 44 """ 45 Non recursive algorithm 46 Based on pop/insert elements in current list 47 """ 48 49 2 39.0 19.5 0.0 new_array = array[:] 50 2 6.0 3.0 0.0 ind = 0 51 2 2.0 1.0 0.0 while True: 52 20002 7778.0 0.4 7.4 try: 53 21010 13528.0 0.6 12.9 while isinstance(new_array[ind], list): 54 1008 1520.0 1.5 1.4 item = new_array.pop(ind) 55 21014 13423.0 0.6 12.8 for inner_item in reversed(item): 56 20006 59375.0 3.0 56.5 new_array.insert(ind, inner_item) 57 20000 9423.0 0.5 9.0 ind += 1 58 2 2.0 1.0 0.0 except IndexError: 59 2 2.0 1.0 0.0 break 60 2 1.0 0.5 0.0 return new_array Total time: 0.137481 s File: funcs.py Function: tishka_flatten at line 63 Line # Hits Time Per Hit % Time Line Contents ============================================================== 63 @profile 64 def tishka_flatten(data: Iterable) -> List: 65 """ 66 Non recursive algorithm 67 Based on append/extend elements to new list 68 69 """ 70 2 17.0 8.5 0.0 nested = True 71 1012 1044.0 1.0 0.8 while nested: 72 1010 1063.0 1.1 0.8 new = [] 73 1010 992.0 1.0 0.7 nested = False 74 112018 38090.0 0.3 27.7 for i in data: 75 111008 50247.0 0.5 36.5 if isinstance(i, list): 76 1008 1431.0 1.4 1.0 new.extend(i) 77 1008 1138.0 1.1 0.8 nested = True 78 else: 79 110000 42052.0 0.4 30.6 new.append(i) 80 1010 1406.0 1.4 1.0 data = new 81 2 1.0 0.5 0.0 return data Total time: 0.062931 s File: funcs.py Function: zart_flatten at line 84 Line # Hits Time Per Hit % Time Line Contents ============================================================== 84 @profile 85 def zart_flatten(a: Iterable) -> List: 86 """ 87 Non recursive algorithm 88 Based on pop from old and append elements to new list 89 """ 90 2 20.0 10.0 0.0 queue, out = [a], [] 91 21012 12866.0 0.6 20.4 while queue: 92 21010 16849.0 0.8 26.8 elem = queue.pop(-1) 93 21010 17768.0 0.8 28.2 if isinstance(elem, list): 94 1010 1562.0 1.5 2.5 queue.extend(elem) 95 else: 96 20000 13813.0 0.7 21.9 out.append(elem) 97 2 53.0 26.5 0.1 return out[::-1] Total time: 0.052754 s File: funcs.py Function: recursive_flatten_generator at line 100 Line # Hits Time Per Hit % Time Line Contents ============================================================== 100 @profile 101 def recursive_flatten_generator(array: Iterable) -> List: 102 """ 103 Recursive algorithm 104 Looks like recursive_flatten_iterator, but with extend/append 105 106 """ 107 1010 1569.0 1.6 3.0 lst = [] 108 22018 13565.0 0.6 25.7 for i in array: 109 21008 17060.0 0.8 32.3 if isinstance(i, list): 110 1008 6624.0 6.6 12.6 lst.extend(recursive_flatten_generator(i)) 111 else: 112 20000 13622.0 0.7 25.8 lst.append(i) 113 1010 314.0 0.3 0.6 return lst Total time: 0.054103 s File: funcs.py Function: recursive_flatten_iterator at line 116 Line # Hits Time Per Hit % Time Line Contents ============================================================== 116 @profile 117 def recursive_flatten_iterator(arr: Iterable) -> Iterator: 118 """ 119 Recursive algorithm based on iterator 120 Usual solution to this problem 121 122 """ 123 124 22018 20200.0 0.9 37.3 for i in arr: 125 21008 19363.0 0.9 35.8 if isinstance(i, list): 126 1008 6856.0 6.8 12.7 yield from recursive_flatten_iterator(i) 127 else: 128 20000 7684.0 0.4 14.2 yield i Total time: 0.056111 s File: funcs.py Function: tishka_flatten_with_stack at line 131 Line # Hits Time Per Hit % Time Line Contents ============================================================== 131 @profile 132 def tishka_flatten_with_stack(seq: Iterable) -> List: 133 """ 134 Non recursive algorithm 135 Based on zart_flatten, but build on try/except pattern 136 """ 137 2 24.0 12.0 0.0 stack = [iter(seq)] 138 2 5.0 2.5 0.0 new = [] 139 1012 357.0 0.4 0.6 while stack: 140 1010 435.0 0.4 0.8 i = stack.pop() 141 1010 328.0 0.3 0.6 try: 142 1010 330.0 0.3 0.6 while True: 143 22018 17272.0 0.8 30.8 data = next(i) 144 21008 18951.0 0.9 33.8 if isinstance(data, list): 145 1008 997.0 1.0 1.8 stack.append(i) 146 1008 1205.0 1.2 2.1 i = iter(data) 147 else: 148 20000 15413.0 0.8 27.5 new.append(data) 149 1010 425.0 0.4 0.8 except StopIteration: 150 1010 368.0 0.4 0.7 pass 151 2 1.0 0.5 0.0 return new

Graphiques

Résultat global:

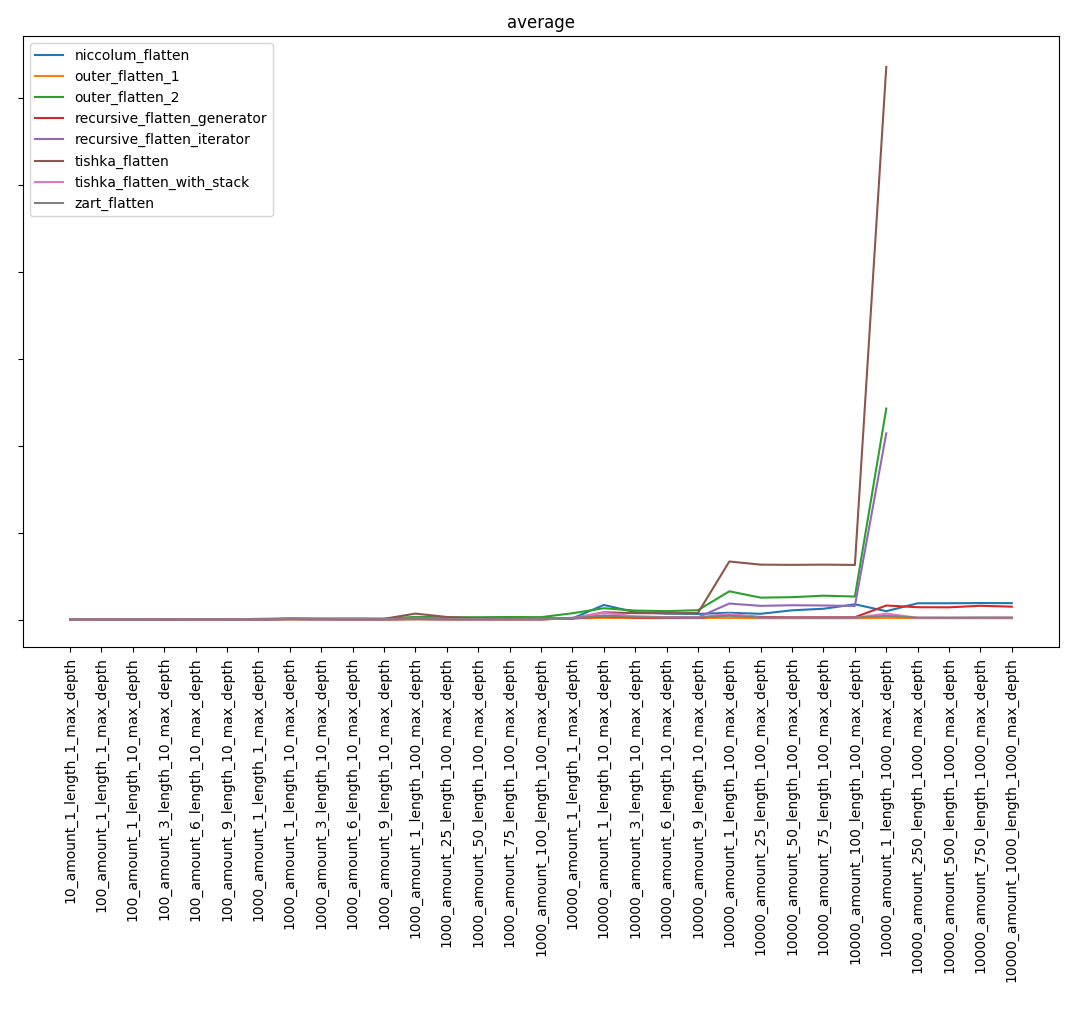
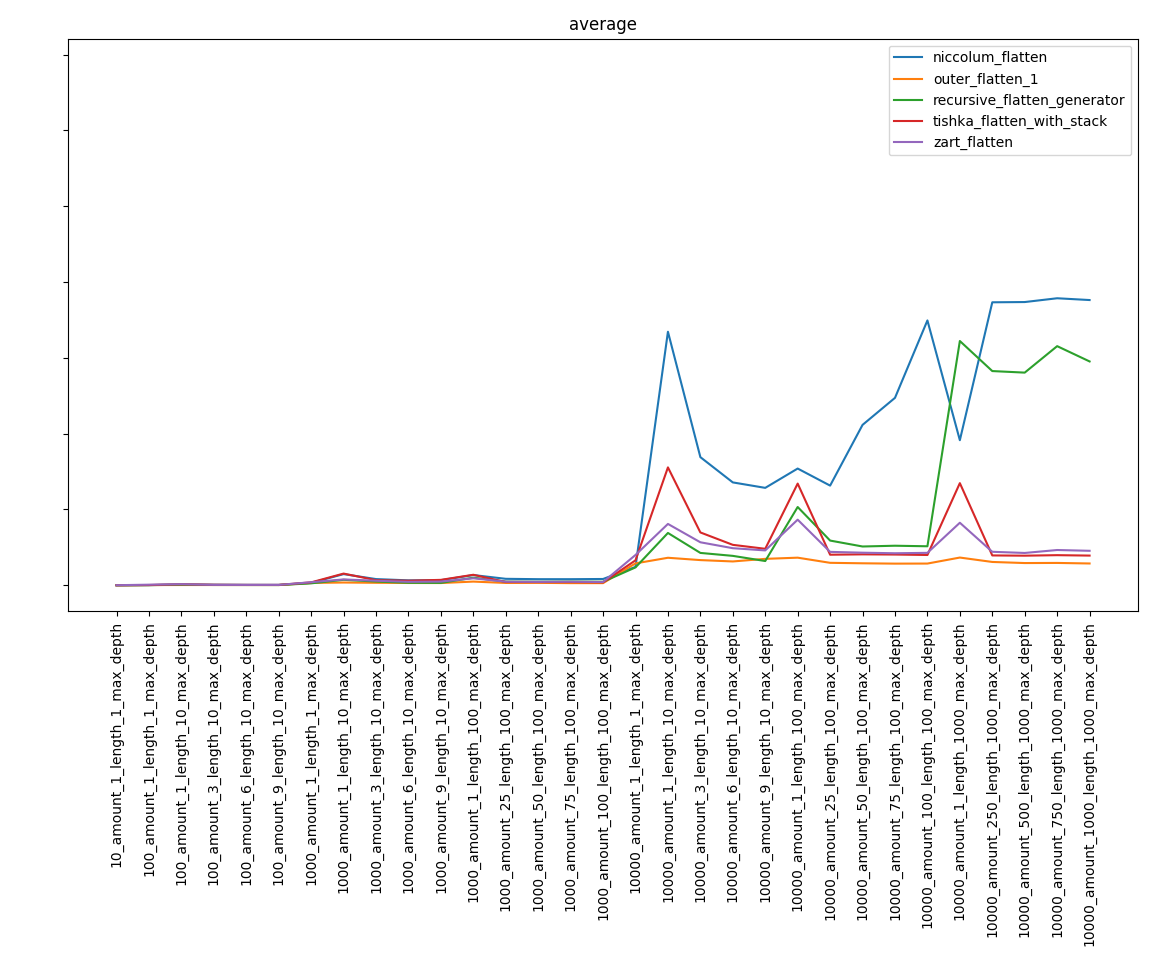
En excluant les fonctions les plus lentes, nous obtenons:

Partie 4. Conclusions

Je dirai peut-être la chose évidente, mais, malgré la complexité connue des algorithmes, le résultat peut ne pas être évident. Ainsi, la fonction niccolum_flatten, dont la complexité était la plus élevée, est entrée dans la phase finale et s'est éloignée de la dernière place. Et recursive_flatten_generator s'est avéré être beaucoup plus rapide que recursive_flatten_iterator.

Pour résumer, je tiens tout d'abord à dire qu'il s'agissait davantage d'une étude que d'un guide pour la rédaction d'algorithmes efficaces de déballage de liste. Habituellement, vous pouvez écrire l'implémentation la plus simple sans vous demander si c'est la plus rapide, car peu d'économies.

Liens utiles

Des résultats plus complets peuvent être trouvés ici.
Référentiel avec code ici
Documentation via sphinx ici

Si vous trouvez des erreurs, écrivez au télégramme Niccolum ou à lastsal@mail.ru.
Je me ferai un plaisir de formuler des critiques constructives.

Déballage des listes imbriquées de profondeur indéfinie

Partie 1. Fonctions

Implémentations empruntées

externe_flatten_1

external_flatten_2

Implémentations propres

niccolum_flatten

tishka_flatten

zart_flatten

recursive_flatten_iterator

recursive_flatten_generator

tishka_flatten_with_stack

Partie 2. Données

create_data_decreasing_depth

create_data_increasing_depth

generate_data

Partie 3. Résultats

CPU Profiler

Graphiques

Partie 4. Conclusions

Liens utiles

More articles: