Posit-arithmétique: vaincre un point flottant dans son propre champ. Partie 1

2e partie

Du traducteur: Le sujet du format Posit était déjà sur le hub ici , mais sans détails techniques significatifs. Dans cette publication, j'attire votre attention sur une traduction d'un article de John Gustafson (auteur de Posit) et Isaac Yonemoto sur le format Posit.
Étant donné que l'article a un grand volume, je l'ai divisé en deux parties. La liste des liens se trouve à la fin de la deuxième partie.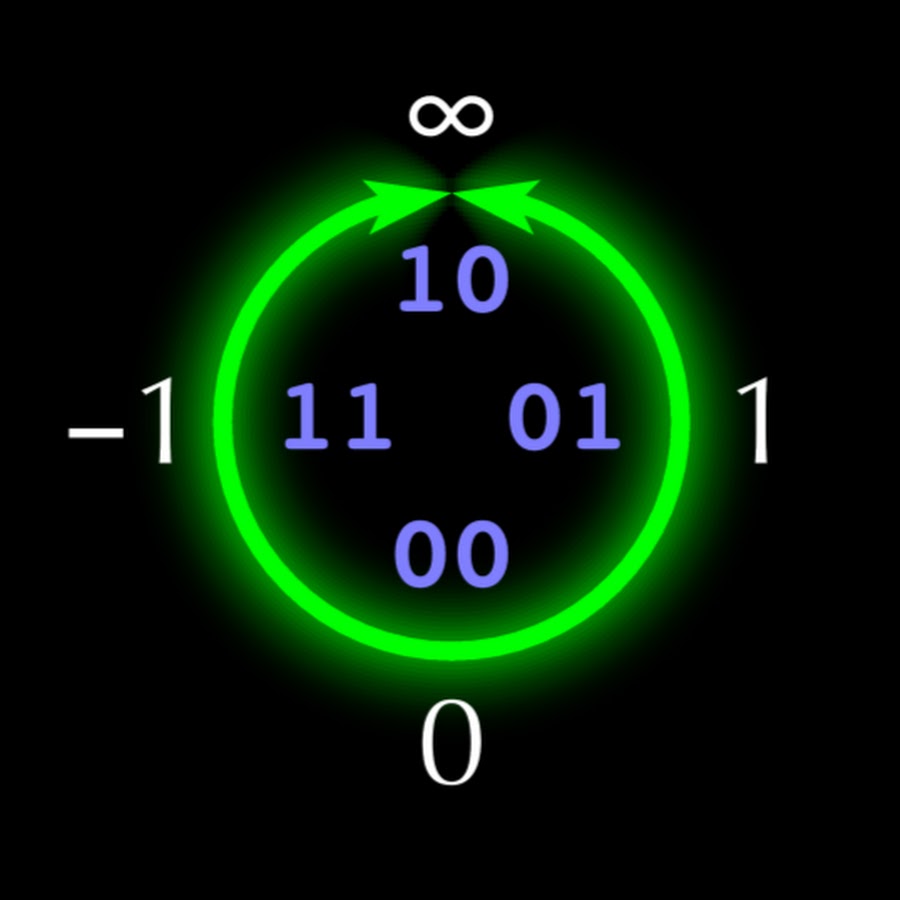



Le nouveau type de données, appelé posit, est conçu pour remplacer directement les nombres à virgule flottante de la norme IEEE 754. Contrairement à la forme précédente, l'arithmétique unum, la norme posit ne nécessite pas l'utilisation d'arithmétique d'intervalle ou d'opérandes de taille variable et, comme float, les nombres positifs sont arrondis si le résultat ne peut pas être représenté exactement. Ils présentent des avantages indéniables par rapport au format flottant, notamment une plus grande plage dynamique, une plus grande précision, une coïncidence au niveau du bit des résultats des calculs sur différents systèmes, un matériel plus simple et une prise en charge plus simple des exceptions. Les nombres positifs ne débordent ni à l'infini ni à zéro, et «pas un nombre» (pas un nombre, NaN) sont des actions, pas des combinaisons de bits. L'unité de traitement de posit est moins complexe que le FPU IEEE. Il consomme moins d'énergie et occupe une zone de silicium plus petite, de sorte que la puce peut effectuer beaucoup plus d'opérations sur les nombres positifs par seconde que FLOPS, avec les mêmes ressources matérielles. Les GPU et les processeurs d'apprentissage en profondeur, en particulier, peuvent effectuer plus d'opérations par watt de consommation d'énergie, ce qui améliorera la qualité de leur travail.

Des tests complets ont été effectués en comparant posit et float en termes de précision de calcul pour diverses précision de posit. Les nombres de position avec une faible précision sont la meilleure solution pour les «calculs approximatifs» dans les cas où une faible précision est acceptable. Les valeurs de position de haute précision offrent une précision supérieure à un flotteur de même taille; dans certains cas, une position de 32 bits peut remplacer en toute sécurité un flotteur de 64 bits. En d'autres termes, posit surpasse le flotteur dans son propre jeu.

Théorie: Unums: Type I et Type II

Le cadre arithmétique unum (nombres universels, nombre universel) a plusieurs formes pour représenter les nombres. La forme originale est «Type I», un surensemble de IEEE 754; elle utilise ubit à la fin de la partie fractionnaire pour indiquer que le nombre réel est exact ou dans la plage entre les nombres réels adjacents. Malgré le fait qu'Unum, comme float, ait un signe, un exposant et une partie fractionnaire, les longueurs de l'exposant et de la partie fractionnaire varient automatiquement, d'un bit à une certaine valeur définie par l'utilisateur. Unum Type I est un moyen compact de représenter l' arithmétique d'intervalle, mais les longueurs variables nécessitent un effort supplémentaire. Ce type peut répéter le comportement d'un flottant à l'aide d'une fonction d'arrondi spéciale.

La forme de nombre universel «Type II» [4] n'est pas compatible avec le flotteur IEEE et est un concept propre et mathématiquement rigoureux basé sur des nombres réels projectifs x. L'idée clé ici est que les entiers signés dans le code complémentaire mappent élégamment aux nombres réels projectifs, avec la même propriété de passer des nombres positifs aux nombres négatifs et avec le même ordre sur l'axe des nombres. Citant William Kahan [5]:
«Ils économisent de l'espace mémoire car ils ne manipulent pas les nombres, mais pointent vers des valeurs. Et cela permet de rendre l'arithmétique très, très rapide. "
La structure de l'unum à 5 bits est représentée sur la Fig. 1. Si chaque unum a n bits, alors le «u-lattice» remplit le quadrant supérieur droit du cercle avec un ensemble ordonné de $$$2 ^ {n-3} -1$ nombres réels $$$x_i$ (pas nécessairement rationnel). Dans le quadrant supérieur gauche sont négatifs $$$x_i$ réfléchi par rapport à l'axe vertical. La moitié inférieure du cercle contient des nombres qui sont inverses aux nombres de la moitié supérieure, réfléchis par l'axe horizontal, ce qui rend les opérations de multiplication et de division aussi symétriques que l'addition et la soustraction. Comme pour le type I, les nombres unum de type II se terminent par 1 (ubit), représentant l'intervalle ouvert entre des points exacts adjacents pour lesquels unum se termine par 0 .


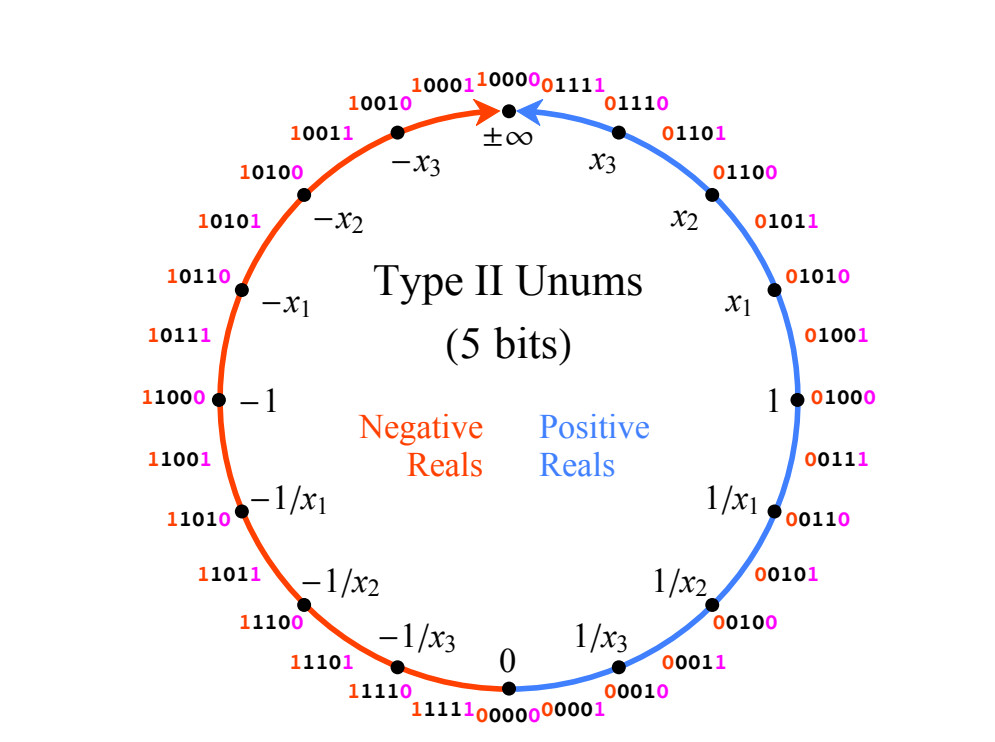Fig. 1. La ligne de nombres réels projectifs, mappée à des entiers dans un code supplémentaire de 4 bits.

Les nombres unum de type II ont de nombreuses propriétés mathématiques idéales, mais la plupart des opérations avec eux sont effectuées à l'aide de tables de recherche . Si n bits de précision sont nécessaires, alors la table (dans le pire des cas) aura $$$2 ^ {2n}$ valeurs pour la fonction de deux arguments, mais en tenant compte des symétries et autres astuces, le tableau peut être réduit à une taille plus acceptable. La taille du tableau limite l'échelle de ce format ultrarapide à 20 bits ou moins pour la technologie d'aujourd'hui. Les numéros unum de type II ne se prêtent pas non plus bien aux opérations de fusion . Ces lacunes ont servi de motivation pour trouver un format qui conserve de nombreuses propriétés des nombres unum de type II, mais qui est plus «matériel» et peut être calculé par des circuits logiques similaires aux FPU existants.

2. Les nombres Posit et Valid

Il existe deux approches opposées aux calculs en nombres réels:

• Pas stricte, mais bon marché et acceptable pour un grand nombre d'applications pratiques
• Rigueur mathématique, même au prix du temps et de la mémoire

La première instruction concerne l'arithmétique réelle, dans laquelle l'erreur d'arrondi est suffisamment petite, la seconde instruction concerne l'arithmétique d'intervalle. Les nombres unum des types I et II peuvent également être considérés dans la même veine, et c'est l'une des raisons pour lesquelles il s'agit de «nombres universels». Cependant, si nous allons toujours utiliser une fonction pour l'arrondi après chaque opération, il vaut mieux ne pas utiliser le dernier bit comme un bit significatif de la partie fractionnaire et non comme ubit. Le nombre unum de ce type sera appelé le nombre positif.

Citation du New Oxford American Dictionary, 3e édition:

posit (nom): Une déclaration faite en supposant que cela se révélera vrai.

Afin de simplifier l'implémentation matérielle, les nombres unum de type II affaiblissent l'une des règles: les valeurs inverses exactes n'existent que pour 0, $$$\ pm \ infty$ et degrés deux. Cela nous permet de remplir la grille en U afin que les nombres finaux restent similaires à flottants, et auront la forme $$$m \ cdot2 ^ k$ où k et m sont des entiers. Il n'y a pas d'intervalles ouverts.

Valide est une paire de nombres positifs de taille égale, chacun se terminant par ubit. Ils sont destinés à être utilisés dans les applications où il est important de déterminer strictement dans quel intervalle le nombre est, par exemple, lors du débogage d'algorithmes numériques. Les valeurs valides sont plus puissantes que l'arithmétique d'intervalle ordinaire et moins susceptibles d'élargir rapidement les limites d'intervalle trop pessimistes [2, 4]. Cependant, ils ne font pas l'objet de cette publication.

La figure 2 montre la structure de la représentation positive à n bits avec des bits d'exposant.


Figure 2. Format de position généralisé pour les valeurs non nulles de fin

Le bit de signe contient 0 pour les nombres positifs, 1 pour les négatifs. Pour les nombres négatifs, recherchez le supplément 2 avant de décoder le mode, l'exposant et la partie fractionnaire. Pour comprendre les bits de mode, considérons les chaînes binaires présentées dans le tableau 1, dans lesquelles k signifie la longueur de la séquence de tête et x dans le train de bits signifie un état indifférent.

Tableau 1. Signification de la longueur de course k des bits de régime



Nous appelons la longueur de la séquence de tête le mode numérique. Les chaînes binaires commencent par un certain nombre de zéros ou de uns consécutifs, suivis du bit opposé, ou la fin de la chaîne est atteinte. Les bits de mode sont surlignés en orange, le bit opposé est surligné en marron. Soit m le nombre de bits identiques dans la séquence, si ces bits sont nuls, alors k = -m, si 1, alors k = m-1. La plupart des processeurs peuvent trouver la première unité dans un mot ou le premier zéro dans un mot dans le matériel, c'est-à-dire que la logique de décodage est déjà disponible. Mode signifie un facteur d'échelle égal à $$$utilisé ^ k$ où $$$utilisé = 2 ^ {2 ^ {es}}$ . Le tableau 2 montre un exemple de valeurs utilisées.

Tableau 2. utilisé comme fonction es



Les bits suivants (surlignés en bleu sur la figure) sont l'exposant e, qui fait référence à un entier non signé. Il n'est pas décalé, comme dans les flottants, il représente la mise à l'échelle $$$2 ^ e$ . Il peut y avoir jusqu'à es bits d'exposant, selon le nombre de bits restant à droite des bits de mode. C'est une façon compacte de modifier la précision; les nombres proches de 1 en valeur absolue ont une plus grande précision que les très grands ou très petits nombres, qui sont beaucoup moins courants dans les calculs.

S'il reste des bits après le mode et des bits d'exposant, ils représentent la partie fractionnaire, f, tout comme la partie fractionnaire 1.f au format float, mais le bit caché est toujours 1. Il n'y a pas de nombres dénormalisés avec 0 caché, contrairement à float.

Le système que nous avons décrit est une conséquence naturelle du remplissage de la grille en u. Commençons par un simple pos 3 bits, pour plus de clarté, sur la fig. La figure 3 ne montre que la moitié droite des nombres réels projectifs. Ainsi, les chiffres de la fig. 3. Obéissez aux règles de type II. Il n'y a que deux valeurs spéciales: 0 (tous les bits sont 0) et ± ∞ (une unité suivie de tous les zéros), leur séquence de bits ne suit pas la notation positionnelle. Pour les autres valeurs positives de la figure 3., les bits sont colorés comme décrit ci-dessus. Notez que toutes les valeurs positives de la figure 3 sont des valeurs exactes utilisées en degré k représentées par des bits de mode.


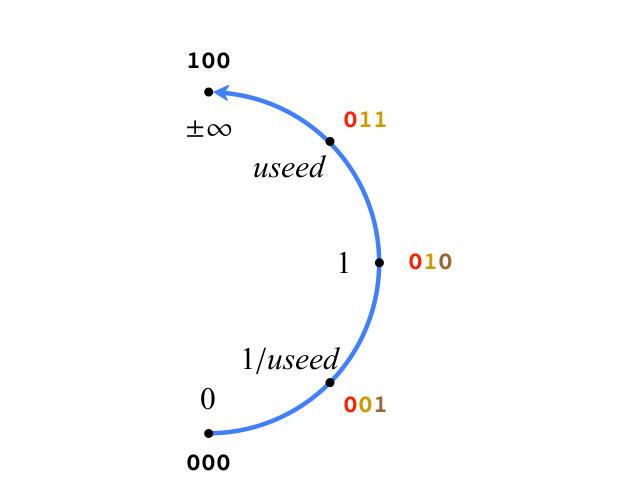Fig.3. Valeurs positives de position 3 bits

La précision des nombres Posit augmente à mesure que les bits sont ajoutés et les valeurs restent là où elles se trouvent sur le cercle lorsque le bit 0 est ajouté. Lorsque 1 est ajouté, une nouvelle valeur est créée entre les deux valeurs Pos sur le cercle. Quelle valeur numérique devons-nous leur attribuer? Soit maxpos la plus grande valeur positive et minpos la plus petite valeur positive sur le cercle défini par la chaîne de bits. Dans la figure 3, maxpos est utilisé et minpos est 1 / utilisé. Les règles d'interpolation sont les suivantes:

Entre maxpos et ± ∞, la nouvelle valeur est maxpos × utilisée; entre 0 et minpos, la nouvelle valeur est minpos / utilisée (avec un nouveau bit de mode)
Entre les valeurs existantes $$$x = 2 ^ m$ et $$$y = 2 ^ n$ , où m et n diffèrent de plus de 1, la nouvelle valeur sera leur moyenne géométrique, $$$\ sqrt {x \ cdot y} = 2 ^ {(m + n) / 2}$ (avec un nouveau bit d'exposant).
Dans d'autres cas, la nouvelle valeur est située au milieu entre les x et y existants, c'est-à-dire qu'il s'agit d'une moyenne arithmétique, $$$(x + y) / 2$ (avec un nouveau bit fractionnaire)

A titre d'exemple, fig. 4 montre la construction de nombres positifs de 2 à 5 bits avec es = 2, et donc utilisé = 16.


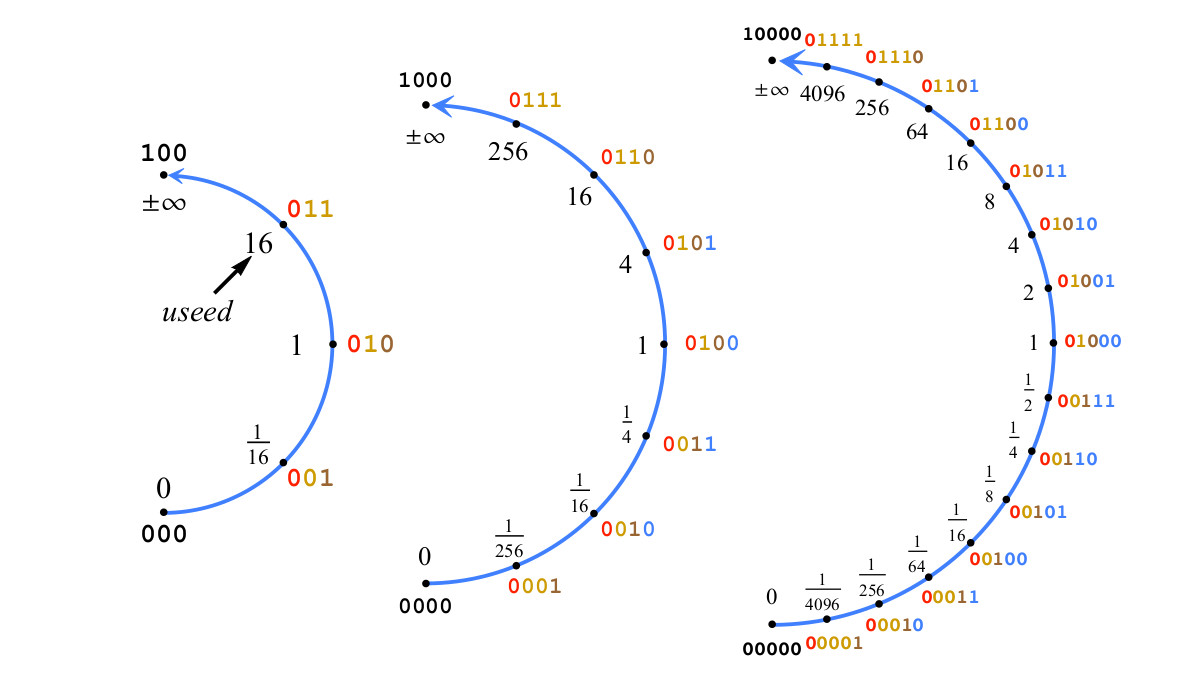Fig. 4. Construire une position avec deux bits d'exposant, $$$es = 2, utilisé = 2 ^ {2 ^ {es}} = 16$

Si dans la fig. 4 ajoutez un bit de plus pour obtenir un posit de 6 bits, aux nombres de posit représentant les plages de valeurs entre 1/16 et 16, le bit de la partie fractionnaire sera ajouté, pas le bit exposant. Considérons une chaîne de bits représentant le nombre pos p comme un entier signé, allant de $$$-2 ^ {n-1}$ avant $$$2 ^ {n-1} -1$ . Soit k un entier représentant des bits de mode, e un nombre non signé représentant des bits d'exposant, s'il est présent. Si l'ensemble de bits est une partie fractionnaire $$$\ {f_1f_2 ... f_ {f_s} \}$ éventuellement vide puis soit f une valeur représentant un nombre $$$1, f_1f_2 ... f_ {f_s}$ . Alors p représente

$$

$$x = \ begin {cases} 0, & p = 0, \\ \ pm \ infty, & p = -2 ^ {n-1}, \\ signe (p) \ fois utilisé ^ k \ fois 2 ^ e \ times f \, & \ text {any other} p \ end {cases}$$

Le mode et les bits es remplissent la même fonction que les bits exponentiels dans le flotteur standard, ensemble ils déterminent un facteur d'échelle égal à une puissance de deux, et chaque incrément utilisé signifie un décalage $$$2 ^ {es}$ peu. Le nombre de maxpos est $$$utilisé ^ {n-2}$ et minpos est égal $$$utilisé ^ {2-n}$ . Un exemple de décodage du nombre positif est présenté sur la figure 5 (avec une valeur «non standard» pour es, pour simplification).


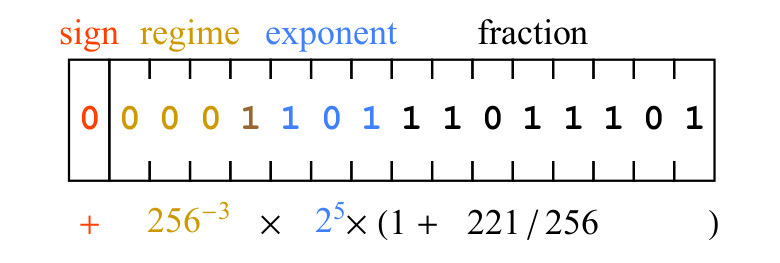Fig. 5. Un exemple de la chaîne de bits positifs et sa signification mathématique

Un peu de signe 0 signifie que la valeur est positive. Les bits du mode 0001 ont une séquence de trois zéros, ce qui signifie que k = -3, par conséquent, le facteur d'échelle introduit par les bits du mode est $$ . Les bits d'exposant, 101, représentent 5 comme un entier binaire non signé, et le facteur d'échelle d'insertion est $$ . Enfin, les bits de la partie fractionnaire 11011101 représentent le nombre 221, c'est-à-dire que la partie fractionnaire est 1 + 221/256. Expression écrite sous le champ binaire de la figure 5. nous mène au résultat $$

2.2. Formation au réseau de neurones et de positons 8 bits

Malgré le fait que la norme IEEE ne définit pas de flottants 8 bits, les nombres positifs de 8 bits avec es = 0 ont prouvé leur utilité à certaines fins, ils sont très utiles pour la construction de réseaux de neurones [3, 8]. Actuellement, les nombres IEEE à demi-précision (16 bits) sont souvent utilisés à ces fins, mais les nombres positifs à 8 bits peuvent potentiellement être traités 2 à 4 fois plus rapidement. Une fonction importante dans les réseaux de neurones est la sigmoïde, qui a une asymptote de 0 pour $$$x \ to- \ infty$ et 1 pour $$$x \ à \ infty$ . Vue générale de la fonction sigmoïde $$$1 / (1 + e ^ {- x})$ , et il est coûteux pour les calculs, et peut facilement nécessiter plus d'une centaine de cycles du processeur pour appeler la fonction exp (x) à partir de la bibliothèque, et à cause de la division. Avec les nombres positifs, vous pouvez simplement inverser le premier bit du nombre positif représentant x, déplacer le nombre 2 bits vers la droite, en remplissant les bits à gauche par des zéros et la fonction positive résultante, illustrée à la figure 6. violet, proche du sigmoïde (montré en vert), et a même la même pente en traversant l'axe y.


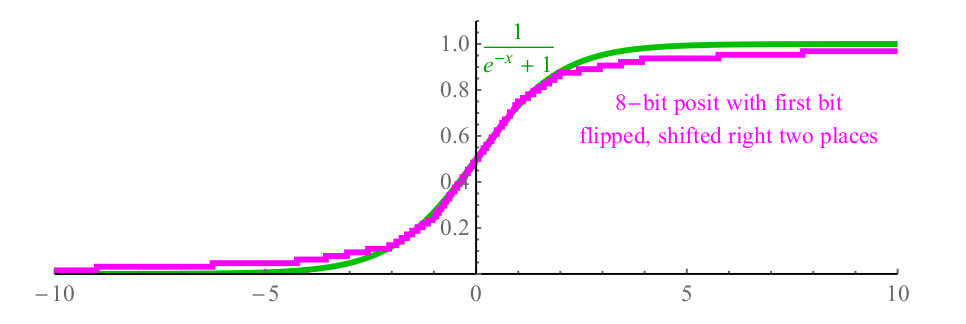Fig. 6. Fonction sigmoïde rapide utilisant la représentation positive

2.3. Utilisé pour atteindre et dépasser la plage dynamique du flotteur

Nous définissons la plage dynamique du système numérique comme le nombre de décimales de la plus petite à la plus grande valeur finale positive, de minpos à maxpos. Autrement dit, la plage dynamique est définie comme $$$log_ {10} (maxpos) −log_ {10} (minpos) = log_ {10} (maxpos / minpos)$ . Pour un posit 8 bits avec es = 0, minpos est 1/64 et maxpos est 64, donc la plage dynamique est de 3,6 ordres décimaux. Les nombres positifs définis avec es = 0 sont élégants et simples, mais leurs versions 16 et 32 ​​bits ont une plage dynamique plus petite qu'un flotteur IEEE de la même taille. Par exemple, un flottant IEEE 32 bits a une plage dynamique de 83 décennies, mais un pos 32 bits avec es = 0 aura une plage dynamique de seulement 18 décennies.

Vous trouverez ci-dessous un tableau des valeurs es qui permettent aux nombres positifs de dépasser la plage dynamique du flottant pour les tailles 16 et 32 ​​bits, et de s'en approcher pour les tailles 64, 128 et 256 bits.

Tableau 3. Plages dynamiques de flottement et de position pour un nombre égal de bits



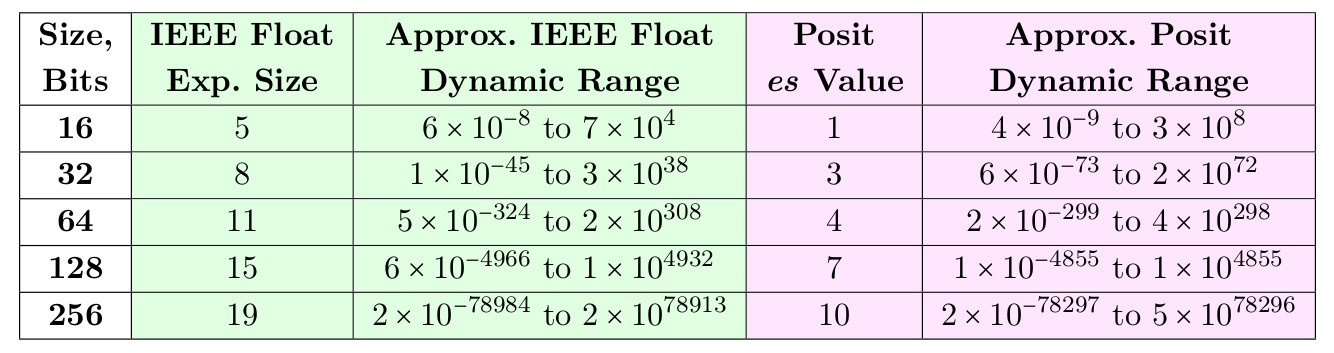
L'une des raisons de choisir es = 3 pour la position 32 bits est que dans ce cas, ils peuvent servir de remplacement simple non seulement pour un flottant 32 bits, mais aussi pour 64 bits. De même, la plage dynamique de 17 décennies pour les positions 16 bits leur ouvre la voie dans les applications qui utilisent actuellement des flottants 32 bits. Nous montrons que posit peut surpasser le flotteur à la fois dans la plage dynamique et la précision à la même taille de bit.

2.4. Comparaison qualitative des formats Float et Posit

Il n'y a pas de «NaN» dans le format posit, à la place, les calculs sont interrompus et le gestionnaire d'interruption doit soit signaler une erreur, soit traiter l'erreur d'une manière ou d'une autre et continuer le calcul, mais les nombres posit ne permettent pas l'affectation d'une certaine valeur qui signale une erreur logique , qui, par définition, est le nombre. Cela simplifie considérablement le matériel. Si le programmeur voit la nécessité d'utiliser des valeurs NaN, cela montre que le programme n'est pas encore terminé et que des nombres valides doivent être utilisés dans l'environnement de débogage pour rechercher et éliminer ces erreurs. En outre, posit n'a pas $$$+ \ infty$ et $$$- \ infty$ , comme float, cependant, les nombres valides prennent en charge les intervalles ouverts $$$(maxpos, + \ infty)$ et $$$(- \ infty, -maxpos)$ , qui permettent de représenter une valeur illimitée de n'importe quel signe, et le besoin d'infini signé signifie seulement qu'au lieu de nombres positifs, vous devez appliquer des valeurs valides.

De plus, dans la vue positive, il n'y a pas de «zéro négatif», zéro négatif, c'est un autre défaut logique qui existe dans la norme flottante IEEE. Avec des nombres positifs, si a = b, alors f (a) = f (b). La norme IEEE 754 dit que le nombre inverse de -0 est $$$- \ infty$ et le nombre inverse de +0 est $$$+ \ infty$ , mais dit également que -0 est +0. Par conséquent, il est entendu que $$$- \ infty = + \ infty$ ?

Les nombres flottants ont un algorithme de comparaison sophistiqué a = b. Si l'un des éléments (a, b) est NaN, le résultat de la comparaison est toujours négatif, même si leur représentation binaire est la même. Si la représentation binaire est différente, alors il y a toujours la possibilité que a soit égal à b, puisqu'un zéro négatif est égal à un zéro positif! En posix, le contrôle d'égalité est le même que pour les entiers: si les bits sont égaux, les nombres sont égaux. Si un bit est différent, ils ne sont pas égaux. Les nombres positifs ont la même relation (a <b) que les entiers signés comme avec les entiers signés, vous devez vous assurer qu'il n'y a pas de débordement avec un changement de signe, mais vous n'avez pas besoin d'instructions machine distinctes pour comparer posit, si vous avez des instructions pour comparer les entiers signés.

Dans le format positif, il n'y a pas de nombres dénormalisés, c'est-à-dire qu'il n'y a pas de combinaison de bits spéciale montrant que le bit caché est 0 au lieu de 1 . Posit n'utilise pas d'anti-débordement, à la place, une diminution progressive de la précision est utilisée, qui fournit la fonctionnalité d'anti-débordement et son cas symétrique, débordement (contrairement à posit, le flotteur standard est asymétrique et utilise ces modèles de bits pour représenter un ensemble important et inutile de valeurs NaN).

Le format float a un avantage sur posit, lors du développement du matériel, une disposition fixe des bits de l'exposant et de la partie fractionnaire permet de les décoder en parallèle.Au format positif, vous devez suivre une séquence, décodant d'abord les bits de mode, puis les bits restants. Il existe un moyen simple de contourner cette restriction, similaire à une astuce utilisée pour augmenter la vitesse de gestion des exceptions dans float: quelques bits supplémentaires sont attachés à chaque valeur afin de stocker des informations de taille en eux lors du décodage de l'instruction.

3. Compatibilité au niveau du bit et opérations combinées

L'une des raisons pour lesquelles IEEE float ne donne pas des résultats identiques sur différents systèmes est que pour les fonctions élémentaires, telles que $$$log(x)$ et $$$cos(x)$IEEE ne nécessite pas de précision jusqu'au dernier bit pour toute entrée possible. L'environnement positif devrait arrondir correctement tous les résultats des opérations arithmétiques prises en charge. (Certains programmeurs de bibliothèque de mathématiques s'inquiètent du «dilemme de dilemme de table», qui est que pour certaines valeurs, il peut être très coûteux de déterminer leur arrondi correct, cela peut être éliminé en utilisant des tables d'interpolation au lieu d'approximations polynomiales.) Valeur incorrecte dans le dernier bit de la fonction$$$e^x$, par exemple, peut finalement conduire à un système informatique nous disant que 2 + 2 = 5.

La raison la plus fondamentale pour laquelle le flotteur IEEE ne produit pas de résultats en double sur différents systèmes est que la norme permet l'utilisation de méthodes voilées pour éviter le débordement / l'anti-débordement et pour augmenter la précision des opérations, telles que le stockage en interne d'un bit de transport supplémentaire pour exponentiel et fractionnaire pièces. L'arithmétique positive interdit de telles astuces cachées.

La dernière version (2008) de la norme IEEE 754 [7] inclut une opération de multiplication-addition combinée dans les exigences. Il s'agit d'un changement controversé, non approuvé par de nombreux membres du comité. Les opérations combinées retardent l'opération d'arrondi jusqu'à ce que la dernière opération du calcul, qui comprend plusieurs opérations, soit terminée une fois toutes les opérations terminées, y compris les opérations entières exactes. La combinaison des opérations n'est pas la même chose que l'arithmétique de précision extensible, qui peut augmenter la longueur des entiers jusqu'à ce que la mémoire de l'ordinateur soit pleine.

L'environnement positif nécessite la présence des opérations combinées suivantes:

Multiplication-addition combinée$$$(a\times b)+c$
Combinaison addition-multiplication $$$(a+b)\times c$
Multiplication-Multiplication-Soustraction Combinée $$$(a\times b)-(c\times d)$
Sommation combinée $$$\sum a_i$
Multiplication scalaire combinée $$$\sum a_i b_i$

Notez que toutes les opérations de la liste ci-dessus sont un sous-ensemble de la multiplication scalaire combinée [6] en termes d'exigences matérielles du processeur. Le plus petit nombre non nul pouvant être obtenu en utilisant la multiplication scalaire est$$$minpos^2$ . Tout produit est un temps entier $$$minpos^2$ . Si nous voulons obtenir un produit scalaire de vecteurs $$$\{maxpos, minpos\}$ et $$$\{maxpos, minpos\}$ comme une opération exacte dans une zone à gratter, nous avons besoin d'un tout assez grand pour stocker $$$maxpos^2/minpos^2$ . Rappelez-vous que $$$maxpos=useed^{n-2}$ et $$$minpos=1/maxpos$ . De cette façon $$$maxpos^2/minpos^2=useed^{4n-8}$ .En tenant compte des bits de transfert et d'arrondi à la puissance de deux, nous obtenons les valeurs recommandées données dans le tableau 4.

Tableau 4. Tailles exactes de la batterie pour chaque taille positive.



Dans certains cas, la taille de la batterie est comparable à la taille du registre, dans d'autres cas, une zone de travail équivalente au cache L1 ou L2 est requise. Les opérations combinées peuvent être exécutées sous forme logicielle ou matérielle, mais doivent être disponibles pour être exécutées dans un environnement positif.