Comment l'intrication quantique contribuera à la détection des ondes gravitationnelles

Nous avons récemment fait une expérience pour tester une nouvelle approche de réduction du bruit quantique dans LIGO et écrit un article à ce sujet, voir arXiv: «Démonstration de l'amélioration de l'interféromètre par l'intrication EPR» . Et ici, je vais vous dire quel type de bruit quantique dans LIGO, comment ils peuvent être réduits, et qu'est-ce que l'intrication quantique et la lumière comprimée ont à voir avec cela.

Article UPD publié dans Nature Photonics .

1. Sensibilité LIGO et bruit quantique

J'ai parlé en détail du fonctionnement du détecteur et du bruit qu'il contient dans la dernière publication sur le télescope Einstein . Le détecteur a une grande variété de bruits: sismiques, thermiques, quantiques et autres - et tous interfèrent avec l'enregistrement d'un signal provenant d'ondes gravitationnelles.


Les principales contributions à la sensibilité du LIGO à différentes fréquences, normalisées à l'amplitude du GW (déformation).

Toute la difficulté de créer un détecteur d'ondes gravitationnelles est de réduire ces bruits. La plupart de ces bruits ne sont pas fondamentaux, mais plutôt des limitations techniques. Et seuls les bruits quantiques proviennent de la nature même de l'appareil de mesure. Ils deviendront le principal obstacle à une meilleure sensibilité des futurs détecteurs, nous allons donc nous attarder sur eux plus en détail. Il existe deux bruits quantiques: le bruit de grenaille et le bruit de pression de rayonnement.

Le bruit de tir provient de la nature quantique du laser: le faisceau laser est constitué de photons volant avec des retards aléatoires différents entre eux. Lorsque ces photons sont mesurés sur des photodiodes, les fluctuations du flux de photons conduisent à des fluctuations de courant et, par conséquent, à du bruit dans le signal que nous observons.

Le bruit de la pression de rayonnement est le deuxième côté de la nature quantique de la lumière. Comme l’électromagnétisme classique le sait depuis le temps des expériences de Lebedev, un objet sur lequel brille la lumière subit une pression de la lumière . Il est facile de comprendre si nous considérons un photon comme une particule: chaque particule porte une impulsion, qui est transmise au corps lors de l'impact. C'est-à-dire que lorsque le laser brille sur un miroir mobile, le miroir commence à se déplacer sous l'influence de la pression lumineuse. Et puisque les photons sont distribués de façon aléatoire, parfois plus de photons arrivent au miroir pendant un intervalle de temps donné, parfois moins, et cette force de pression lumineuse est également aléatoire. Donc: la quantification de la lumière conduit à une force aléatoire agissant sur les miroirs du LIGO. Cette force provoque un décalage aléatoire des miroirs, qui est enregistré à la sortie de l'interféromètre sous forme de signal parasite.


Explication sur le bruit quantique. Une distribution aléatoire du nombre de photons produit une force aléatoire de pression de rayonnement (à gauche). En revanche, une distribution aléatoire des photons dans le temps entraîne des fluctuations d'amplitude sur le photodétecteur (à droite). Les deux bruits dépendent de la longueur d'onde, de la puissance lumineuse et de la longueur des épaules. Le bruit de la pression de radiation est moindre, plus la masse des miroirs est grande. Crédit: [1].

Le bruit de la pression de rayonnement est d'autant plus fort que la puissance de la lumière incidente sur les miroirs est élevée (c'est-à-dire le flux de photons). Le signal du GW augmente également avec l'augmentation de la puissance lumineuse dans le détecteur. Le bruit de tir normalisé au signal diminue. En conséquence, il s'avère que vous pouvez augmenter la sensibilité limitée par le bruit de tir en augmentant la puissance de la lumière, mais vous devrez payer pour cela avec l'augmentation du bruit de la pression de rayonnement. Et vice versa. Il n'y a aucun moyen de manière classique de supprimer les deux bruits quantiques à la fois. Devra utiliser la technologie quantique.


Dépendance de la sensibilité à la puissance lumineuse: le bruit de tir (bleu) diminue et le bruit de pression de rayonnement (vert) augmente proportionnellement.

2. Lumière comprimée

Il y a un merveilleux article sur Habré sur la lumière comprimée de qbertych . Si vous ne savez pas ce qu'est la lumière compressée, je vous recommande fortement de lire d'abord son article. Je serai bref.

Si vous regardez la lumière comme une onde, les paramètres caractéristiques ne seront pas le flux de photons et le retard entre eux, mais l'amplitude et la phase de l'onde. Habituellement, ils parlent de quadratures de phase et d'amplitude de lumière.

$$$$ afficher $$ E = E_0 \ cos (\ omega_0 t + \ phi) = E_0 \ cos \ omega_0 t \ cos \ phi - E_0 \ sin \ omega_0 t \ sin \ phi = \\ = E_ {} \ sin \ omega_0 t + E_ {a} \ cos \ omega_0 t $$ afficher $$

Si le signal qui nous intéresse est contenu dans la phase de lumière, et qu'il est suffisamment petit, alors nous pouvons faire une approximation:

$$$$ afficher $$ E_ {f} = E_0 \ sin \ phi \ approx E_0 \ phi; \ quad E_ {a} = E_0 \ cos \ phi \ environ E_0 $$ afficher $$

Par conséquent, la valeur$$ $ inline $ E_ {f} $ inline $ appelé quadrature de phase - il contient des informations sur la phase.

Par conséquent, le bruit de grenaille est une fluctuation de la phase de la lumière, et le bruit de la pression de rayonnement est provoqué par des fluctuations d'amplitude.

L'incertitude de phase et l'incertitude d'amplitude sont liées par la relation de Heisenberg:

$$$$ afficher $$ \ Delta ^ 2 E_ {f} \ Delta ^ 2 E_ {a} \ leq \ frac {1} {2} $$ afficher $$

Dans un faisceau laser conventionnel, ces incertitudes sont égales. Cependant, il est possible de comprimer l' incertitude dans la phase en augmentant l'incertitude d'amplitude - l'essentiel est que leur produit satisfasse la relation d'incertitude. Une telle lumière est appelée pressée:

$$$$ afficher $$ \ Delta ^ 2 E_ {f} ^ {sqz} = e ^ {- 2r} \ Delta ^ 2 E_ {f}, \ Delta ^ 2 E_ {a} ^ {sqz} = e ^ {2r } \ Delta ^ 2 E_ {a} \\ \ Delta ^ 2 E_ {f} ^ {sqz} \ Delta ^ 2 E_ {a} ^ {sqz} = \ Delta ^ 2 E_ {f} \ Delta ^ 2 E_ { a} \ leq \ frac {1} {2}, $$ display $$

où r est le taux de compression.

D'une manière générale, même en l'absence d'un faisceau puissant, des fluctuations de vide existent toujours. Ils peuvent également être compressés pour obtenir un vide comprimé: en moyenne, le nombre de photons qu'il contient est nul, mais les fluctuations de l'amplitude et de la phase sont compressées.


Ce sont les fluctuations de vide pénétrant dans le détecteur par le port de signal qui sont à l'origine du bruit quantique dans LIGO. Par conséquent, si ce vide est comprimé en phase, cela réduira le bruit de grenaille dans le détecteur.

Cette approche a été utilisée dans le détecteur GEO600 au cours des 8 dernières années, réduisant le bruit des tirs de quatre fois, et depuis cette année, elle a également été mise en œuvre dans LIGO, réduisant le bruit des tirs de moitié (ce qui augmente le nombre d'événements enregistrés de 8 fois).



Gauche: Un exemple de sensibilité LIGO améliorée avec une lumière comprimée. À droite: la meilleure compression à ce jour a été créée dans notre groupe il y a plusieurs années: les fluctuations de vide ont été supprimées de 15 dB.

Cependant, tout n'est pas si simple: selon la relation d'incertitude, si on comprime la phase, on augmente les fluctuations d'amplitude. Et ils augmentent le bruit de la pression de radiation. Et encore une fois, vous devez choisir le bruit à réduire en augmentant l'autre. Mais est-il possible de contourner cette limitation?

3. Compression dépendante de la fréquence

Heureusement, deux bruits quantiques limitent la sensibilité du détecteur à différentes fréquences: à faible bruit, la pression de rayonnement est beaucoup plus forte que la pression de tir, et à haute - vice versa. Par conséquent, il est possible de préparer une compression délicate de la lumière, où à basse fréquence, la lumière est compressée en amplitude (et donc le bruit de pression de rayonnement est réduit), et à haute fréquence - en phase (et donc le bruit de grenaille est réduit).


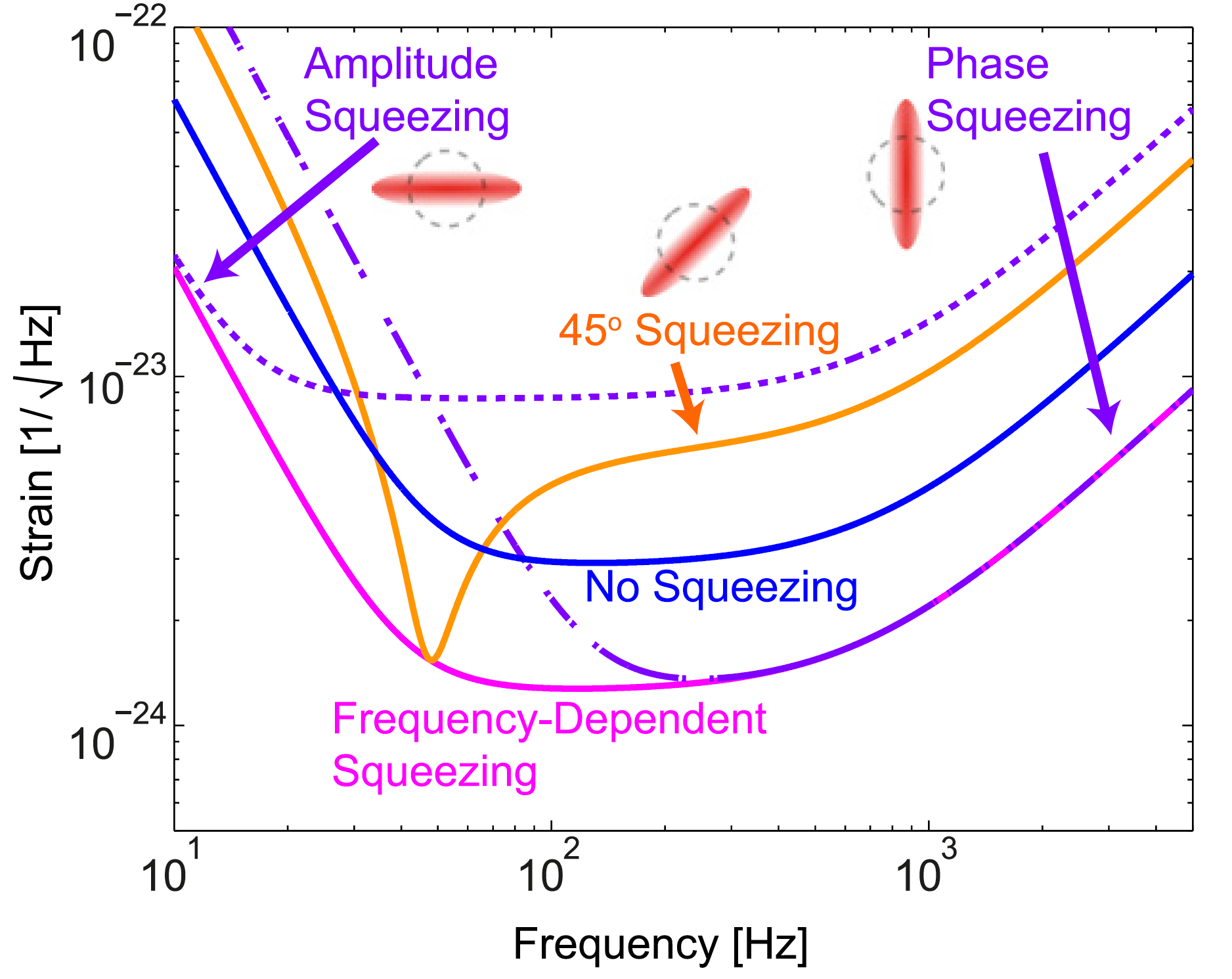Compression dépendante de la fréquence: à différentes fréquences, l'amplitude, la phase ou une combinaison de celles-ci est compressée. En conséquence, la sensibilité est améliorée à toutes les fréquences. [Classe SSY Chua et al 2014. Quantum Grav. 31 183001]

Fondamentalement, la raison de la nécessité d'une compression dépendante de la fréquence est que la pression de rayonnement sur les miroirs crée également une compression légère, mais dans une quadrature différente. Cela peut être vu dans l'image ci-dessous: si vous utilisez une compression conventionnelle à l'entrée, elle acquiert une dépendance de fréquence à la sortie en raison de la pression de rayonnement. Pour "annuler" cette dépendance de fréquence, vous devez définir la dépendance inverse pour la compression à l'entrée.


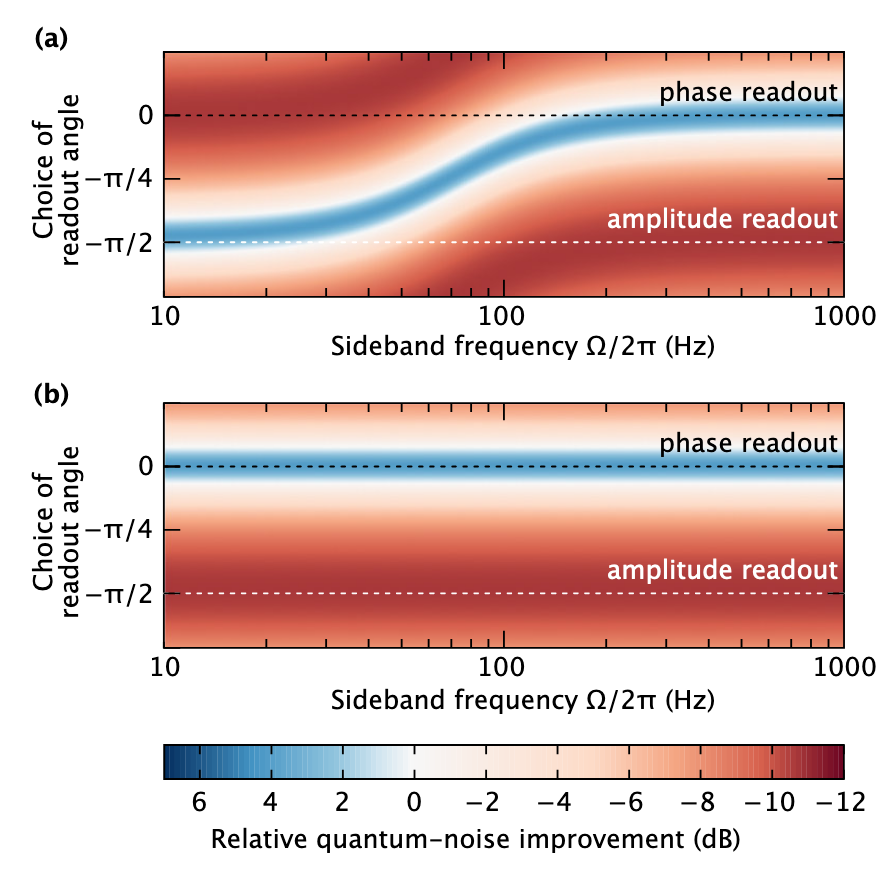Un exemple de l'article: la dépendance de l'amélioration de la sensibilité de l'interféromètre lors de l'utilisation de la compression conventionnelle en fonction de la fréquence et des différentes phases de mesure est montrée ci-dessus - le signal est en quadrature de phase, et on peut voir que si la sensibilité augmente à hautes fréquences (couleur bleue), puis à basses fréquences elle diminue (rouge ) L'utilisation de la compression dépendante de la fréquence peut améliorer la sensibilité à toutes les fréquences.

Donc, nous résolvons conceptuellement le problème de la réduction du bruit quantique à toutes les fréquences, la question demeure: comment mettre en œuvre une telle dépendance en fréquence. Pour ce faire, vous devez comprendre comment transformer la phase compressée en une amplitude compressée. En fait, c'est très simple: pour produire un déphasage:

$$$$ afficher $$ E_ {f} ^ {sqz} = E_0 e ^ {- 2r} \ sin (\ phi) \ rightarrow E_0 e ^ {- 2r} \ sin (\ phi + \ pi / 2) = E_ { a} e ^ {- 2r} $$ afficher $$

Habituellement, un simple miroir suffit pour décaler la phase, ce qui changera la longueur du chemin parcouru par la lumière. Cependant, dans ce cas, vous avez besoin d'un appareil qui crée un déphasage dépendant de la fréquence: ne dépassez pas la phase aux hautes fréquences, mais aux basses$$ $ inline $ \ pi / 2 $ inline $ .

Actuellement, le principal concept de création d'une compression dépendante de la fréquence dans toutes les conceptions des futurs détecteurs est l'utilisation de résonateurs de filtrage supplémentaires. Si le vide comprimé est réfléchi par un tel résonateur lorsqu'il est désaccordé de la fréquence de résonance, il acquiert la dépendance de fréquence nécessaire. Il présente cependant de grandes difficultés: pour créer la dépendance fréquentielle requise, les résonateurs doivent mesurer plusieurs centaines de mètres de long sous vide, ce qui est très coûteux et difficile à contrôler. Nous avons une autre idée.

Le fait est que dans le détecteur lui-même, il existe déjà de nombreux résonateurs de tailles appropriées, de faibles pertes et avec une méthode de contrôle bien connue, mais ils ne peuvent pas être utilisés directement - pour une compression dépendante de la fréquence, un désaccord de la résonance est nécessaire. Mais chaque résonateur a de nombreuses fréquences de résonance, tandis que le détecteur ne fonctionne que sur l'une d'entre elles. L'idée est d'utiliser une résonance différente , reflétant la lumière pressée de l'interféromètre lui-même pour obtenir la dépendance de fréquence nécessaire. La question demeure: comment utiliser la dépendance en fréquence créée à une fréquence différente de la fréquence de travail principale du laser. Et puis l'intrication quantique vient à la rescousse.

4. L'intrication quantique et le paradoxe de l'EPR

La question de la nature de l' enchevêtrement mérite sans aucun doute un article séparé. J'ai discuté un peu plus de complexité dans un article précédent sur le Habré, donc ici je ne décrirai que brièvement ses principales propriétés. Commençons par le paradoxe EPR (Einstein-Podolsky-Rosen): trois messieurs ont remarqué qu'il y a un hic dans la mécanique quantique. D'une part, il y a le principe d'incertitude, qui dit qu'il est impossible de mesurer avec précision les coordonnées et la quantité de mouvement d'une particule en même temps (et dans notre cas, l'amplitude et la phase de la lumière). D'un autre côté, on peut faire une expérience aussi simple: prendre l'événement de désintégration des particules, dans lequel naissent deux particules identiques. Selon la loi de conservation de l'élan, ils se disperseront dans des directions opposées à la même vitesse. Si nous mesurons la quantité de mouvement d'une particule, nous saurons exactement la quantité de mouvement de la seconde. Si nous mesurons la coordonnée de la deuxième particule, nous connaîtrons simultanément exactement à la fois la coordonnée (nous l'avons mesurée) et la quantité de mouvement (nous l'avons prédite à partir de la mesure de la première particule), ce qui, semble-t-il, est impossible en raison de la relation d'incertitude. Le paradoxe visible est résolu en introduisant le concept d'enchevêtrement des particules: deux particules ne sont pas indépendantes l'une de l'autre, elles sont décrites par une fonction d'onde. Cette fonction d'onde est non locale: jusqu'au moment de la mesure, il est impossible de dire laquelle des particules a volé dans quelle direction. Dans un sens, ils volaient tous les deux dans les deux directions à la fois, et seulement au moment de la mesure, il y avait un choix aléatoire de la particule à mesurer. Leurs coordonnées et leur impulsion sont connectées de sorte que la relation d'incertitude ne s'applique pas à leur valeur relative. De plus, si l'une des particules subit une action, par exemple par une certaine force, la deuxième particule «ressent» également cette force - ses paramètres mesurés changeront en conséquence.

Donc, pour nous, la chose la plus importante: si nous avons deux particules, nous pouvons prédire avec précision les propriétés de la deuxième particule en mesurant la première. Nous pouvons mettre une source d'influence sur le chemin d'une particule, et elle agira sur deux à la fois. Après avoir fait la mesure correcte, nous pouvons voir le résultat de cet effet.

Comment nous l'utilisons (il a été proposé pour la première fois dans un article de Nature Physics [2]). Le rôle des particules dans l'EPR est joué par deux faisceaux de vide comprimé à deux fréquences: la fréquence fondamentale de l'interféromètre et la fréquence de la prochaine résonance du résonateur. Nous les confondons, l'un d'eux (haute fréquence) est réfléchi par le résonateur accordé et mesuré. Il obtient une dépendance de fréquence. Les rayons étant enchevêtrés, cette dépendance en fréquence est également transmise au faisceau à la fréquence fondamentale. Après la mesure, nous pouvons prédire les signaux dans le faisceau principal idéalement avec une précision parfaite. Pour ce faire, nous mesurons séparément sur deux détecteurs distincts et traitons de manière optimale les données.


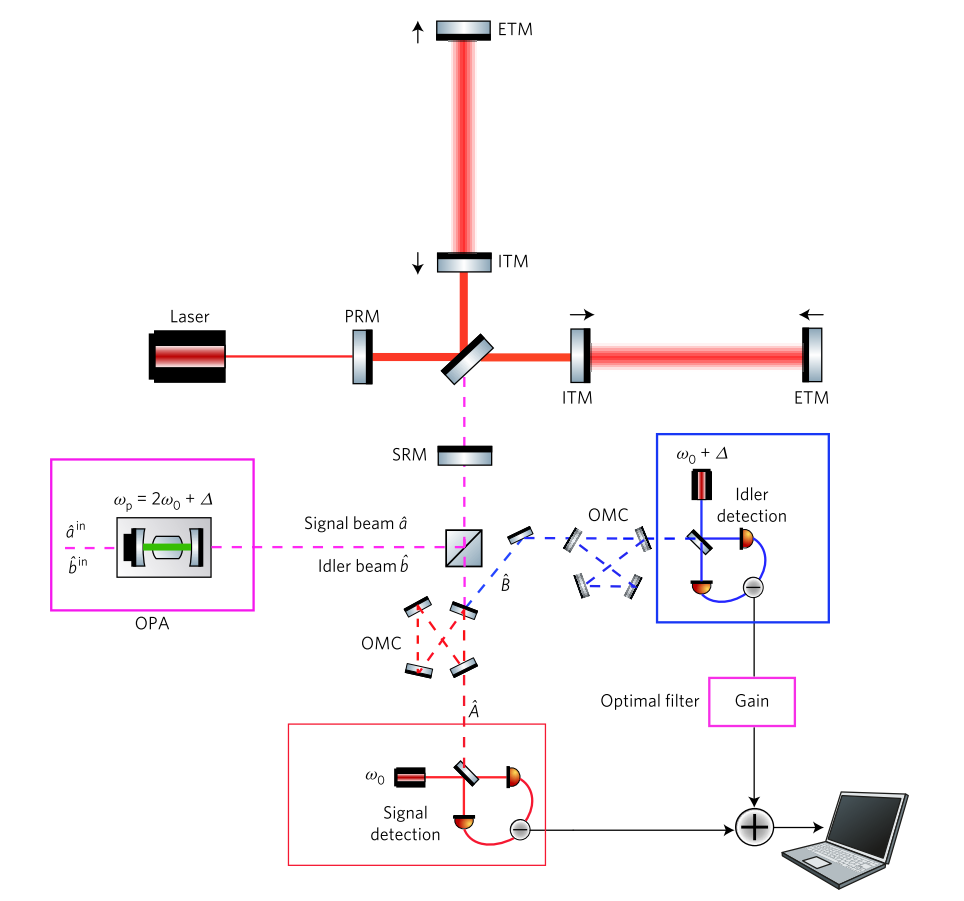Un schéma complet de compression en fonction de la fréquence basé sur l'intrication de [2]. L'OPA (Optical Parametric Amplifier) ​​crée deux faisceaux intriqués de vide comprimé à différentes fréquences, tous deux envoyés au détecteur. Un faisceau à une fréquence porteuse résonne dans l'interféromètre. Un faisceau à haute fréquence est désaccordé de l'une des résonances les plus élevées. En sortie, les rayons sont séparés et détectés sur deux détecteurs homodynes différents, après quoi ils sont traités de manière optimale.

5. Expérience

Notre expérience ne comprend pas d'interféromètre complet avec miroirs mobiles. Au lieu de cela, nous explorons la possibilité d'obtenir une compression dépendante de la fréquence en utilisant la lumière intriquée réfléchie par un résonateur.


Conception expérimentale simplifiée. Au lieu d'un interféromètre complet, nous avons un résonateur optique de 2,5 m de long. Au lieu de deux détecteurs homodynes différents, nous utilisons un détecteur, mais deux faisceaux de référence de fréquences différentes.

Comme je l'ai écrit ci-dessus, dans un interféromètre, la pression de rayonnement crée une dépendance en fréquence de la lumière comprimée, ce qui gâche la sensibilité du détecteur. Afin d'annuler cette dépendance en fréquence, nous devons créer une dépendance en fréquence inverse de la lumière comprimée. Dans notre expérience, la sensibilité ne gâche pas la pression de rayonnement (nous n'avons pas de miroirs mobiles), mais le désaccord du détecteur de la résonance (voir l'image ci-dessous (a)). Mesuré en quadrature de signal (lecture de phase), cela gâche la sensibilité aux basses fréquences (rouge).

Pour restaurer la sensibilité, nous reconstruisons un rayon supplémentaire (oisif) à partir de la résonance dans la direction opposée. Ensuite, après la mesure, nous pouvons restaurer complètement la sensibilité. En termes d'EPR - nous pouvons prédire le résultat de la mesure de la quadrature de phase avec une meilleure précision en utilisant la lumière enchevêtrée quantique.


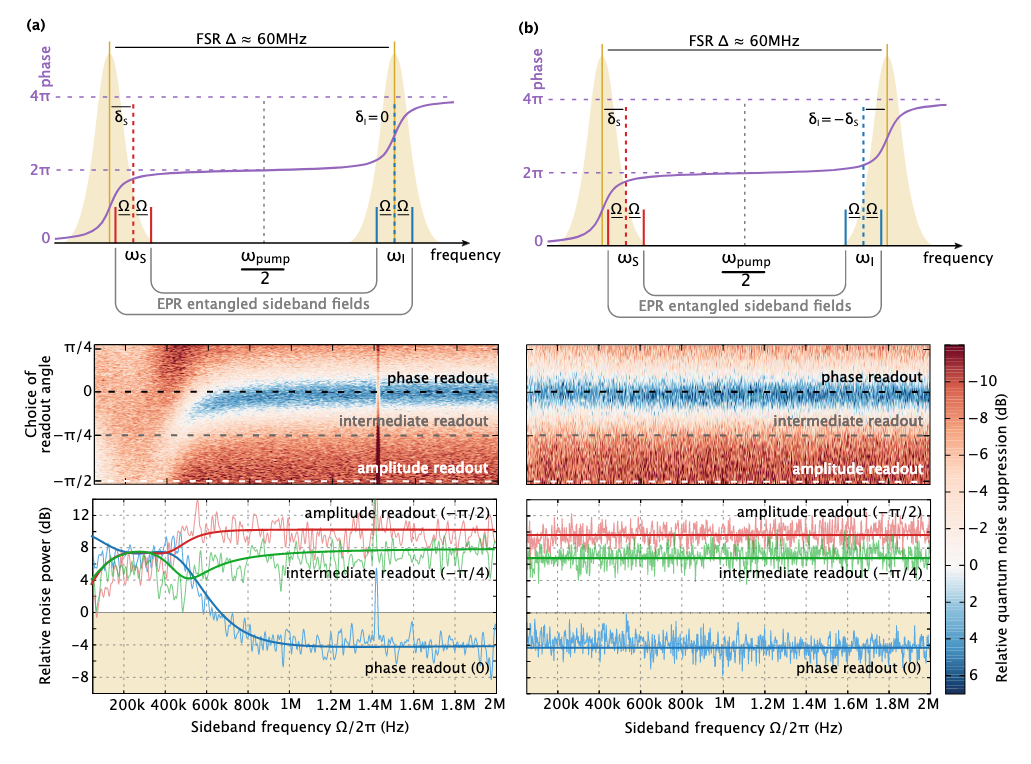Deux expériences pour observer la compression dépendante de la fréquence. Dans le premier (a), nous avons réglé le faisceau de signal de la résonance du détecteur, gâchant ainsi la sensibilité dans la quadrature de phase (et créant une dépendance en fréquence de la lumière comprimée). Dans le second, nous avons créé une dépendance de fréquence supplémentaire du deuxième rayon (oisif) et en raison de l'intrication quantique entre les deux rayons, le signal et le signal ont pu restaurer la sensibilité endommagée en annulant la dépendance de fréquence introduite dans la première expérience.

Dans l'image ci-dessus, la dépendance en fréquence en (a) est assez floue. Cela est dû aux limites du post-traitement: idéalement, deux détecteurs homodynes séparés sont nécessaires, dont les signaux peuvent être filtrés de manière optimale. Cependant, dans un autre mode, nous pouvons obtenir une belle dépendance en fréquence de la lumière comprimée si nous reconstruisons les deux rayons à partir de la résonance dans une direction. Un tel schéma n'est pas pertinent pour le détecteur, mais donne une idée des options d'installation. Eh bien, de belles données expérimentales :)

6. Conclusion

Pour résumer. Les fluctuations quantiques de la lumière sont la source principale et la plus fondamentale de bruit dans tous les détecteurs modernes et futurs. Pour les supprimer, on peut utiliser des corrélations quantiques - lumière comprimée. Cependant, afin de réduire le bruit dans toute la gamme de fréquences du détecteur, il est nécessaire de compresser les fluctuations d'amplitude aux basses fréquences et les fluctuations de phase aux hautes fréquences. Il est proposé que cette compression en fonction de la fréquence soit effectuée à l'aide de résonateurs de filtrage spéciaux. Traditionnellement, de tels résonateurs sont très coûteux et difficiles à mettre en œuvre. Notre alternative consiste à utiliser le détecteur lui-même comme résonateur à filtre, en utilisant de la lumière enchevêtrée quantique. Nous avons fait une expérience et montré que l'intrication quantique permet effectivement de réaliser cette idée.

Cette approche n'est pas une panacée, hélas: il faut payer pour plus de commodité. Pour que le concept fonctionne pleinement, il est nécessaire d'utiliser deux détecteurs homodynes, ce qui est assez difficile expérimentalement. De plus, le deuxième détecteur ajoute du bruit à la sensibilité - bien que beaucoup moins que ce que vous pouvez gagner avec la compression.

Dans ce travail, nous avons joué avec les subtilités et la lumière comprimée et montré comment nous pouvons les utiliser pour améliorer la sensibilité des futurs détecteurs.Mais cela, bien sûr, n'est que la première étape d'un long chemin pour mettre en œuvre cette approche dans un vrai détecteur: vous devez vérifier comment tout fonctionne avec un véritable interféromètre, avec des miroirs mobiles, deux homodynes, etc. En général, le travail est encore complet.

Pour ceux qui sont intéressés par les détails, consultez notre article et l' article où l'idée a été présentée pour la première fois [2].

[1] S. Hild au- delà des détecteurs GW de 2e génération
[2] Y. Ma et al, Proposition de détection des ondes gravitationnelles au-delà de la limite quantique standard par enchevêtrement EPR, Nature Physics volume 13, pages 776–780 (2017)

7. Divers

Et maintenant quelques nouvelles de LIGO:

1. LIGO 26 3. https://gracedb.ligo.org/superevents/public/O3/ , .
2. , , . , , N+1 Scientific American . , .
3. 100 . , (c 55 130 ). , , .
4. LIGO , , , . . LIGO . , , . , , , , .

: , , : @hbar_universe .