Régression linéaire et méthodes pour sa restauration

Source: xkcd

La régression linéaire est l'un des algorithmes de base pour de nombreux domaines liés à l'analyse des données. La raison en est évidente. Il s'agit d'un algorithme très simple et compréhensible, qui a contribué à son utilisation généralisée pendant des dizaines, voire des centaines d'années. L'idée est que nous supposons une dépendance linéaire d'une variable sur un ensemble d'autres variables, puis essayons de restaurer cette dépendance.

Mais cet article ne traite pas de l'application d'une régression linéaire pour résoudre des problèmes pratiques. Nous discuterons ici des caractéristiques intéressantes de la mise en œuvre d'algorithmes distribués pour sa récupération que nous avons rencontrées lors de l'écriture d'un module d'apprentissage automatique dans Apache Ignite . Un peu de mathématiques de base, les bases de l'apprentissage automatique et l'informatique distribuée vous aideront à comprendre comment restaurer la régression linéaire, même si les données sont réparties sur des milliers de nœuds.

De quoi tu parles?

Nous sommes confrontés à la tâche de restaurer la dépendance linéaire. En entrée, de nombreux vecteurs de variables supposées indépendantes sont donnés, chacun étant associé à une certaine valeur de la variable dépendante. Ces données peuvent être représentées sous la forme de deux matrices:

$$

$$\ begin {pmatrix} a_ {11} & a_ {12} & a_ {13} & ... & a_ {1n} \\ a_ {21} & a_ {22} & a_ {23} & ... & a_ {2n} \\ ... \\ a_ {m1} & a_ {m2} & a_ {m3} & ... & a_ {mn} \\ \ end {pmatrix} \ begin {pmatrix} b_ {1} \\ b_ {2} \\ ... \\ b_ {m} \\ \ end {pmatrix}$$

Maintenant, puisque la dépendance est supposée, et en plus d'être linéaire, nous écrivons notre hypothèse sous la forme d'un produit de matrices (pour simplifier la notation ici et ci-dessous, on suppose que le terme libre de l'équation $$$x_n$et la dernière colonne de la matrice $$$A$contient des unités):

$$

$$\ begin {pmatrix} a_ {11} & a_ {12} & a_ {13} & ... & a_ {1n} \\ a_ {21} & a_ {22} & a_ {23} & ... & a_ {2n} \\ ... \\ a_ {m1} & a_ {m2} & a_ {m3} & ... & a_ {mn} \\ \ end {pmatrix} \ times \ begin {pmatrix} x_ { 1} \\ x_ {2} \\ ... \\ x_ {n} \\ \ end {pmatrix} = \ begin {pmatrix} b_ {1} \\ b_ {2} \\ ... \\ b_ {m} \\ \ end {pmatrix}$$

Très similaire à un système d'équations linéaires, non? Il semble, mais très probablement il n'y aura pas de solutions à un tel système d'équations. La raison en est le bruit présent dans presque toutes les données réelles. En outre, la raison peut être l'absence de relation linéaire en tant que telle, que vous pouvez essayer de combattre en introduisant des variables supplémentaires qui dépendent non linéairement de la source. Prenons l'exemple suivant:

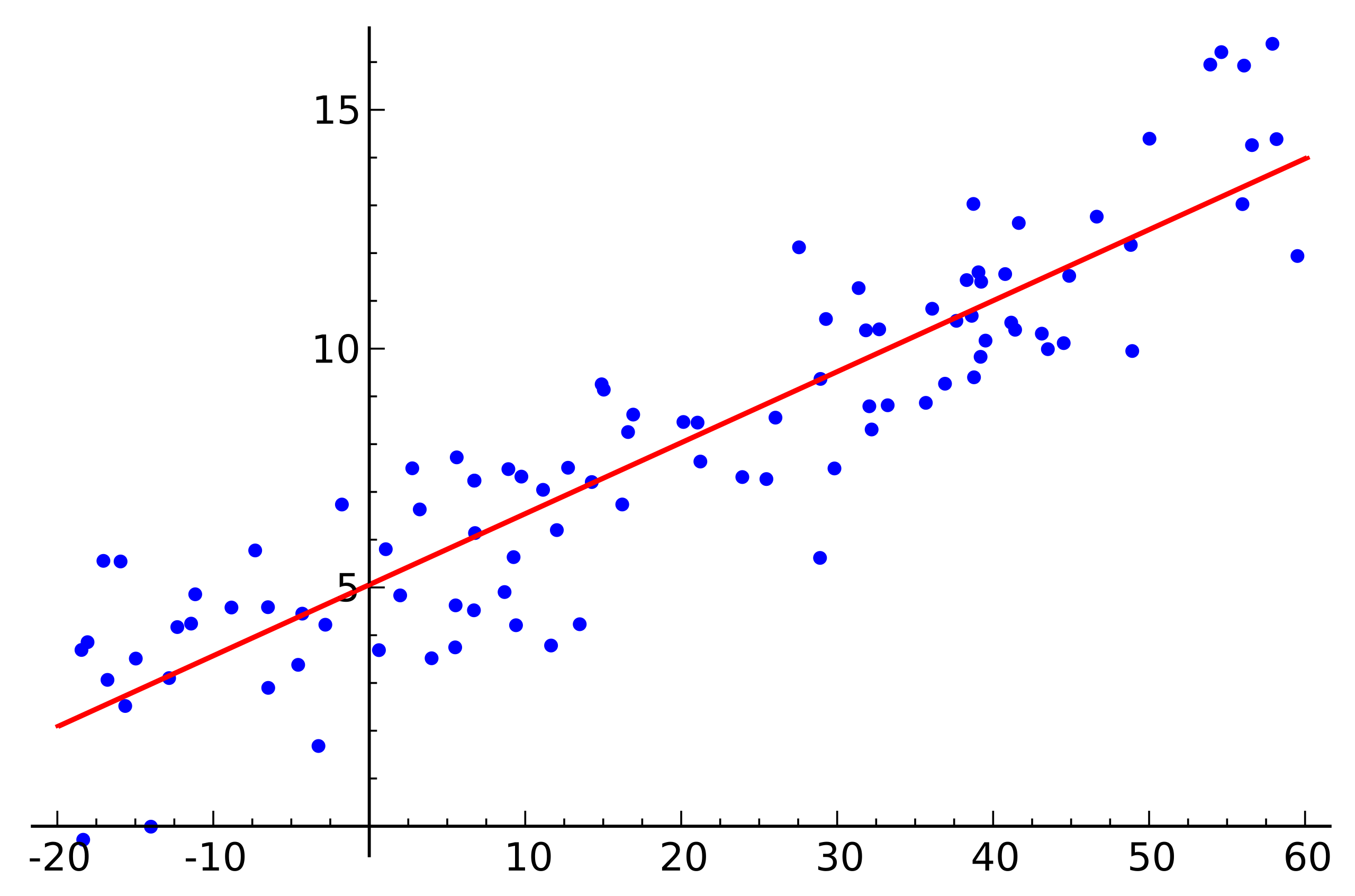Source: Wikipedia

Ceci est un exemple de régression linéaire simple qui montre la dépendance d'une variable (le long de l'axe $$$y$) d'une autre variable (le long de l'axe $$$x$) Pour que le système d'équations linéaires correspondant à cet exemple ait une solution, tous les points doivent se trouver exactement sur une droite. Mais ce n'est pas le cas. Mais ils ne reposent pas sur une même ligne précisément à cause du bruit (ou parce que l'hypothèse de la présence d'une dépendance linéaire était erronée). Ainsi, afin de restaurer une dépendance linéaire à partir de données réelles, il est généralement nécessaire d'introduire une autre hypothèse: les données d'entrée contiennent du bruit et ce bruit a une distribution normale . On peut faire des hypothèses sur d'autres types de distribution du bruit, mais dans la grande majorité des cas, c'est la distribution normale qui sera discutée plus loin.

Méthode du maximum de vraisemblance

Nous avons donc supposé la présence de bruit aléatoire distribué normalement. Comment être dans une telle situation? Dans ce cas, en mathématiques, il existe et est largement utilisée la méthode du maximum de vraisemblance . Bref, son essence réside dans le choix de la fonction de vraisemblance et sa maximisation ultérieure.

On revient à la restauration de la dépendance linéaire à partir de données à bruit normal. Notez que la relation linéaire supposée est une attente mathématique $$$\ mu$distribution normale disponible. Dans le même temps, la probabilité que $$$\ mu$prend l'une ou l'autre valeur, sous réserve de la présence d'observables $$$x$, se présente comme suit:

$$

$$P (\ mu \ mid X, \ sigma ^ 2) = \ prod_ {x \ in X} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \; e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}}}$$

Nous remplaçons maintenant à la place $$$\ mu$et $$$X$variables dont nous avons besoin:

$$

$$P (x \ mid A, B, \ sigma ^ 2) = \ prod_ {i \ in [1, m]} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \; e ^ {- \ frac {(b_i-a_ix) ^ 2} {2 \ sigma ^ 2}}}, a_i \ in A, b_i \ in B$$

Il ne reste plus qu'à trouver le vecteur $$$x$à laquelle cette probabilité est maximale. Pour maximiser une telle fonction, il est commode de faire un prologarithme en premier (le logarithme de la fonction atteindra son maximum au même point que la fonction elle-même):

$$

$$f (x) = ln (\ prod_ {i \ in [1, m]} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \; e ^ {- \ frac {(b_i-a_ix ) ^ 2} {2 \ sigma ^ 2}}}) = \ sum_ {i \ in [1, m]} ln \ frac {1} {\ sigma \ sqrt {2 \ pi}} \; - \ sum_ {i \ in [1, m]} \ frac {(b_i-a_ix) ^ 2} {2 \ sigma ^ 2}$$

Ce qui, à son tour, se résume à minimiser la fonction suivante:

$$

$$f (x) = \ sum_ {i \ in [1, m]} (b_i-a_ix) ^ 2$$

À propos, cela s'appelle la méthode des moindres carrés . Souvent, tout le raisonnement ci-dessus est omis et cette méthode est simplement utilisée.

Décomposition QR

Le minimum de la fonction ci-dessus peut être trouvé si vous trouvez le point auquel le gradient de cette fonction est égal à zéro. Et le gradient sera écrit comme suit:

$$

$$\ nabla f (x) = \ sum_ {i \ in [1, m]} 2a_i (a_ix - b_i) = 0$$

La décomposition QR est une méthode matricielle pour résoudre le problème de minimisation utilisé dans la méthode des moindres carrés. À cet égard, nous réécrivons l'équation sous forme matricielle:

$$

$$A ^ T A x = A ^ Tb$$

Donc, nous exposons la matrice $$$A$sur les matrices $$$Q$et $$$R$et effectuer une série de transformations (l'algorithme de décomposition QR lui-même ne sera pas considéré ici, seulement son utilisation par rapport à la tâche):

$$

$$\ begin {align} & (QR) ^ T (QR) x = (QR) ^ Tb; \\ & R ^ T Q ^ T Q R x = R ^ T Q ^ T b; \\ \ end {align}$$

Matrix $$$Q$est orthogonale. Cela nous permet de nous débarrasser du travail. $$$Q Q ^ T$:

$$

$$\ begin {align} & R ^ T R x = R ^ T Q ^ T b; \\ & (R ^ T) ^ {- 1} R ^ T R x = (R ^ T) ^ {- 1} R ^ T Q ^ T b; \\ & R x = Q ^ T b. \ end {align}$$

Et si vous remplacez $$$Q ^ T b$sur $$$z$ça va finir $$$R x = z$. Étant donné que $$$R$est la matrice triangulaire supérieure, elle ressemble à ceci:

$$

$$\ begin {pmatrix} r_ {11} & r_ {12} & r_ {13} & r_ {14} & ... & r_ {1n} \\ 0 & r_ {22} & r_ {23} & r_ { 24} & ... & r_ {2n} \\ 0 & 0 & r_ {33} & r_ {34} & ... & r_ {3n} \\ 0 & 0 & 0 & r_ {44} & .. . & r_ {4n} \\ ... \\ 0 & 0 & 0 & 0 & ... & r_ {nn} \\ \ end {pmatrix} \ times \ begin {pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ ... \\ x_n \ end {pmatrix} = \ begin {pmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \\ ... \\ z_n \ end {pmatrix}$$

Cela peut être résolu par la méthode de substitution. Objet $$$x_n$c'est comme $$$z_n / r_ {nn}$article précédent $$$x_ {n-1}$c'est comme $$$(z_ {n-1} - r_ {n-1, n} x_n) / r_ {n-1, n-1}$et ainsi de suite.

Il convient de noter ici que la complexité de l'algorithme résultant de l'utilisation de la décomposition QR est $$$O (2mn ^ 2)$. De plus, malgré le fait que l'opération de multiplication matricielle est bien parallélisée, il n'est pas possible d'écrire une version distribuée efficace de cet algorithme.

Descente en pente

En parlant de minimiser une certaine fonction, il vaut toujours la peine de rappeler la méthode de descente (stochastique) du gradient. Il s'agit d'une méthode de minimisation simple et efficace basée sur le calcul itératif du gradient d'une fonction en un point, puis en le déplaçant du côté opposé au gradient. Chacune de ces étapes amène la solution au minimum. Le dégradé est identique:

$$

$$\ nabla f (x) = \ sum_ {i \ in [1, m]} 2a_i (a_ix - b_i)$$

Cette méthode est également bien parallélisée et distribuée en raison des propriétés linéaires de l'opérateur de gradient. Notez que dans la formule ci-dessus, les termes indépendants sont sous le signe de la somme. En d'autres termes, nous pouvons calculer le gradient indépendamment pour tous les indices $$$i$du premier au $$$k$, parallèlement à cela, calculer le gradient des indices avec $$$k + 1$avant $$$m$. Ajoutez ensuite les dégradés résultants. Le résultat de l'addition sera le même que si nous calculions immédiatement le gradient des indices du premier au $$$m$. Ainsi, si les données sont réparties entre plusieurs parties des données, le gradient peut être calculé indépendamment sur chaque partie, puis les résultats de ces calculs peuvent être additionnés pour obtenir le résultat final:

$$

$$\ nabla f (x) = \ sum_ {i \ in P_1} 2a_i (a_ix - b_i) + \ sum_ {i \ in P_2} 2a_i (a_ix - b_i) + ... + \ sum_ {i \ in P_k} 2a_i (a_ix - b_i)$$

En termes de mise en œuvre, cela s'inscrit dans le paradigme MapReduce . À chaque étape de la descente du gradient, une tâche de calcul du gradient est envoyée à chaque nœud de données, puis les gradients calculés sont collectés ensemble et le résultat de leur sommation est utilisé pour améliorer le résultat.

Malgré la simplicité de mise en œuvre et la possibilité d'exécuter dans le paradigme MapReduce, la descente en gradient a également ses inconvénients. En particulier, le nombre d'étapes nécessaires pour atteindre la convergence est beaucoup plus important par rapport à d'autres méthodes plus spécialisées.

LSQR

LSQR est une autre méthode de résolution du problème, qui convient à la fois à la reconstruction de régression linéaire et à la résolution de systèmes d'équations linéaires. Sa principale caractéristique est de combiner les avantages des méthodes matricielles et une approche itérative. Les implémentations de cette méthode se trouvent à la fois dans la bibliothèque SciPy et dans MATLAB . Une description de cette méthode ne sera pas donnée ici (elle peut être trouvée dans l'article LSQR: Un algorithme pour les équations linéaires éparses et les moindres carrés épars ). Au lieu de cela, une approche sera démontrée pour adapter le LSQR à l'exécution dans un environnement distribué.

La méthode LSQR est basée sur la procédure de bidiagonalisation. Il s'agit d'une procédure itérative, dont chaque itération comprend les étapes suivantes:


Mais basé sur le fait que la matrice $$$A$partitionné horizontalement, chaque itération peut être représentée en deux étapes MapReduce. Ainsi, il est possible de minimiser les transferts de données lors de chaque itération (uniquement des vecteurs de longueur égale au nombre d'inconnues):



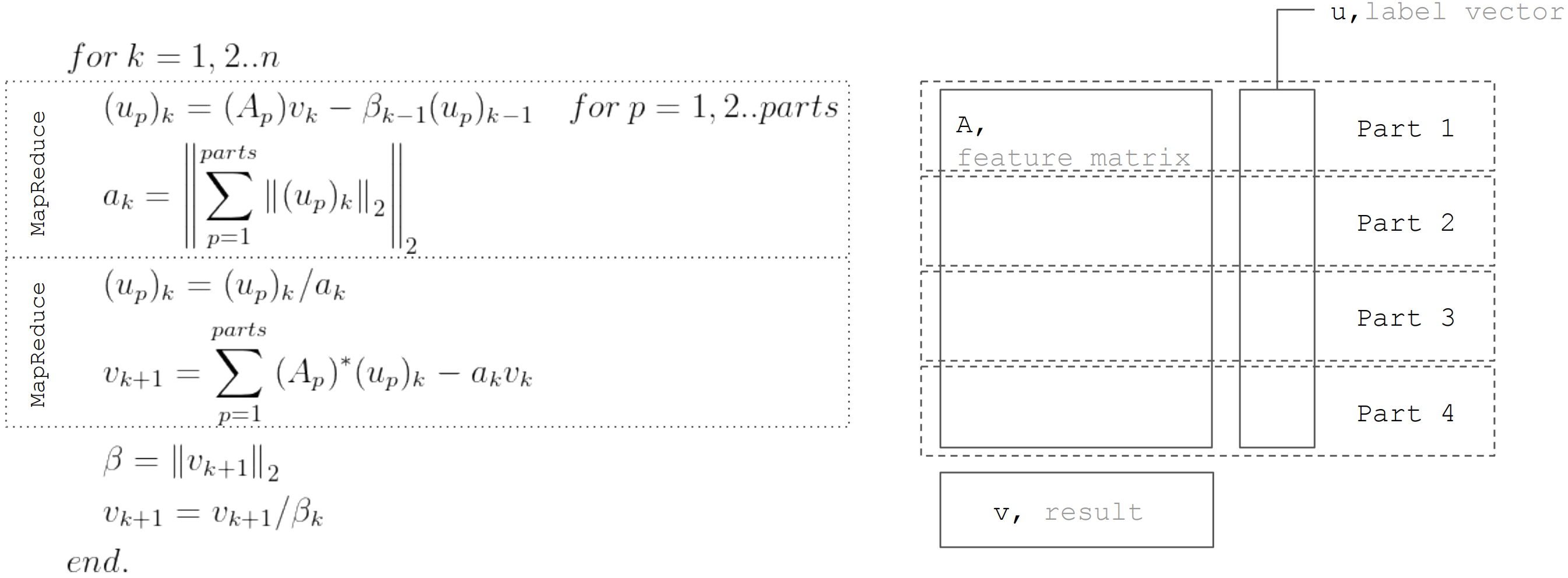
Cette approche est utilisée lors de l'implémentation d'une régression linéaire dans Apache Ignite ML .

Conclusion

Il existe de nombreux algorithmes de récupération par régression linéaire, mais ils ne peuvent pas tous être appliqués dans toutes les conditions. La décomposition QR est donc idéale pour une solution précise sur de petites matrices de données. La descente en pente est simplement implémentée et vous permet de trouver rapidement une solution approximative. Et LSQR combine les meilleures propriétés des deux algorithmes précédents, car il peut être distribué, converge plus rapidement par rapport à la descente en gradient et permet également un arrêt précoce de l'algorithme, contrairement à la décomposition QR, pour trouver une solution approximative.