Dans la plupart des systèmes de conception (CAD), la représentation principale de l'objet simulé est la représentation aux limites de la géométrie ou B-rep (représentation des limites). Mais de plus en plus, les utilisateurs de CAO doivent faire face à des modèles de polygones, par exemple, obtenus à la suite d'une numérisation 3D ou empruntés à des catalogues en ligne.
Pour les rendre aptes à un travail ultérieur, vous devez convertir le maillage polygonal en un modèle B-rep. Et ce n'est pas facile du tout.
Nous avons développé le composant logiciel C3D B-Shaper, qui est intégré au système de conception et convertit les modèles polygonaux en une représentation des limites. Dans cet article, nous montrerons l'algorithme de conversion et des exemples d'implémentation en C ++.




Quel est le principal problème des modèles polygonaux en termes de CAO? Les outils traditionnels ne peuvent pas leur être appliqués - pour effectuer des opérations booléennes, pour construire des chanfreins et des congés, pour obtenir des projections et des sections. Si l'utilisation du modèle B-rep pour construire sa représentation polygonale est assez facile (cela se fait en utilisant la triangulation), alors la transformation inverse est beaucoup plus difficile. Un certain nombre de problèmes se posent - la reconnaissance de surfaces de différents types (y compris des surfaces de forme libre), la présence de bruit, qui sont caractéristiques, par exemple, des résultats de numérisation 3D.

Dans le nouveau SDK, nous avons implémenté un mécanisme en trois étapes pour convertir le modèle polygonal en B-rep: segmentation, reconstruction de surface, construction du modèle B-rep. En général, le processus est supposé être itératif: si pour une raison quelconque l'utilisateur n'est pas satisfait du résultat, il peut alors apporter les changements correctifs nécessaires aux étapes de la segmentation et de la reconstruction des surfaces.


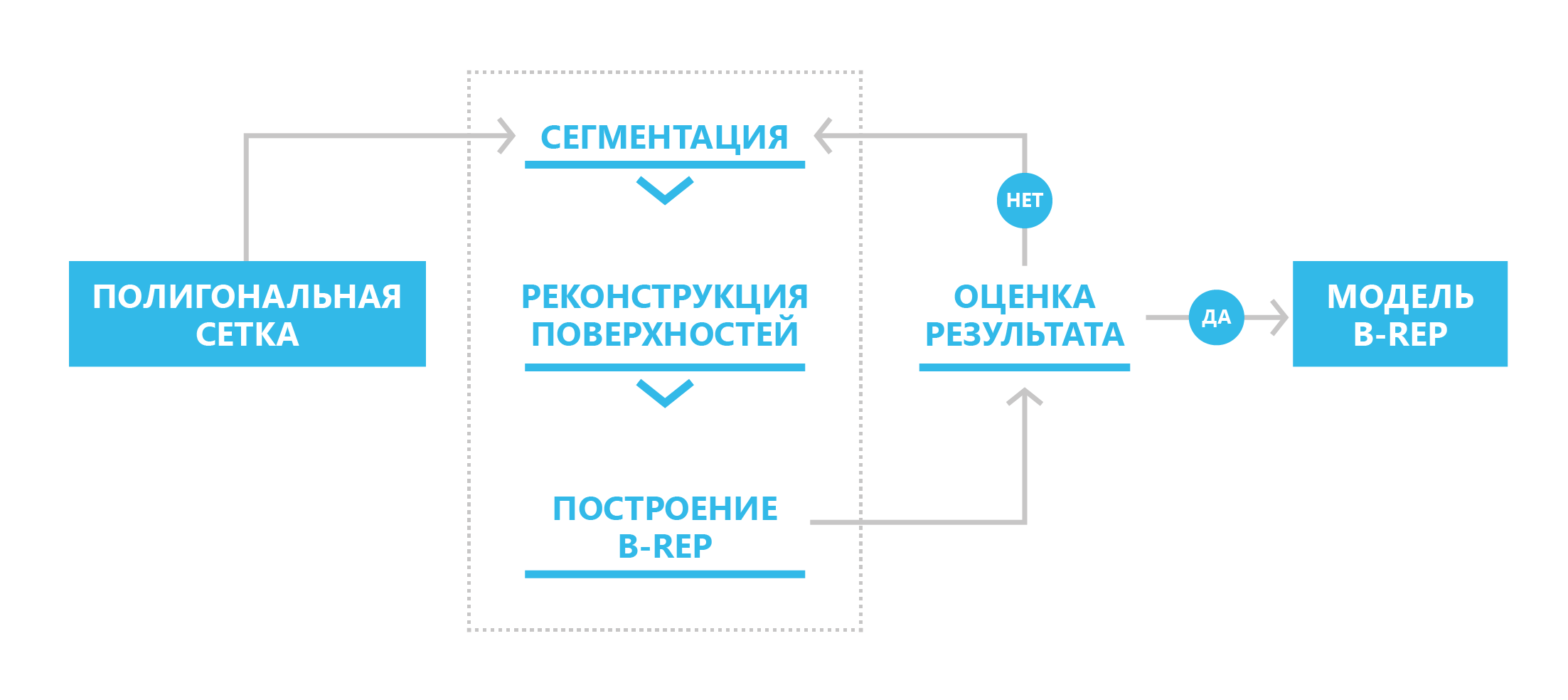Le schéma de conversion d'une représentation polygonale en frontière

Avant de lancer le processus de conversion en B-rep, il est nécessaire, dans certains cas, d'améliorer la qualité du maillage polygonal d'origine: coordonner les directions des normales aux polygones voisins, éliminer les «trous», appliquer des algorithmes de lissage en présence de bruit dans le maillage d'origine.

Segmentation des polygones

À la première étape, l'ensemble initial de polygones maillés est classé en sous-ensembles (segments). Les informations sur les normales aux sommets du maillage permettent une segmentation de premier ordre et assurent ainsi la partition initiale du maillage, ainsi que la classification des zones planes ou fortement incurvées.

Le maillage initial est basé sur la définition de bords dits «pointus» - ces bords entre deux polygones triangulaires dont l'angle entre les normales moyennes dépasse une certaine valeur prédéterminée.

La segmentation de second ordre analyse la grille en fonction de ses courbures principales, ce qui fournit une base suffisante pour la classification des surfaces élémentaires. Dans le calcul des courbures aux sommets de la grille, nous avons utilisé les résultats de Mayer (Mark Meyer, Mathieu Desbrun, Peter Schroder et Alan H. Barr, Opérateurs de géométrie différentielle discrète pour les collecteurs triangulés à 2, Visualisation et Mathématiques III, 2003) pour déterminer le différentiel discret opérateur pour les régions triangulées: pour chaque sommet du maillage d'origine, on considère un ensemble de sommets voisins associés à un sommet donné à travers une arête. Ensuite, un opérateur discret K est calculé pour un sommet donné, sur la base duquel la courbure moyenne normale, moyenne K _H et gaussienne K _G au sommet de la grille est déterminée.


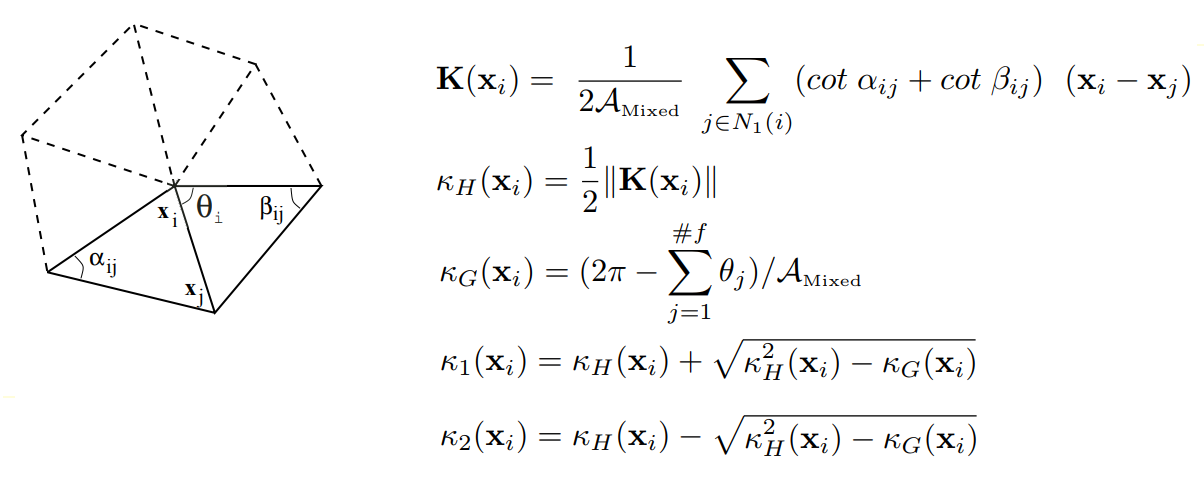Sur la définition d'un opérateur différentiel discret pour les domaines triangulés

Ainsi, le tenseur de courbure pour chaque sommet de la grille est calculé, dont les valeurs propres sont les courbures principales souhaitées K1 et K2 , et les vecteurs propres sont les directions principales du changement de courbure.

Ensuite, les sommets du maillage sont classés en fonction des valeurs des courbures principales K ₁ et K _{2 qui y sont} calculées. L'algorithme de classification des sommets est basé sur la méthode des moyennes k, c'est-à-dire sur la minimisation de la déviation quadratique totale des points de grappe par rapport aux centres de ces grappes. Par conséquent, à la sortie de l'algorithme, chaque sommet de la grille est associé à un certain cluster $$$Ci$et une paire de courbures (centre du cluster) (L. Guillaume, «Segmentation de maillage triangulaire à tenseur de courbure avec rectification des limites», Proceedings Computer Graphics International (CGI), 2004).


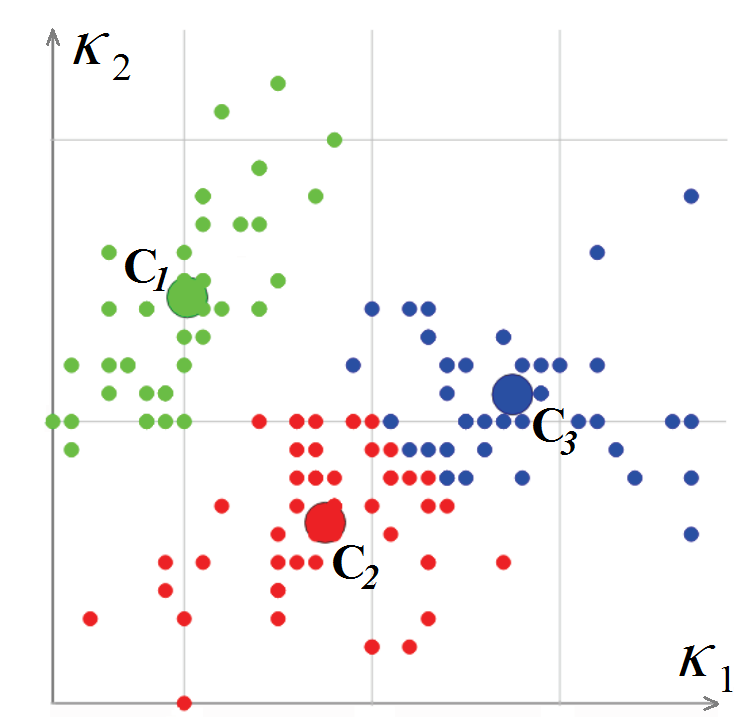Classification des sommets d'un maillage polygonal dans l'espace des courbures

Après avoir classé les sommets du maillage polygonal, il est nécessaire de classer les polygones. Au début de cette procédure, un polygone triangulaire est sélectionné pour lequel la courbure peut être considérée comme complètement définie (les trois sommets appartiennent à un cluster ou deux sommets se trouvent sur une arête vive). Ce polygone est déclaré comme un nouveau segment, et la procédure récursive pour développer le segment commence à partir de lui: pour chaque polygone triangulaire, les polygones qui lui sont adjacents sont considérés, à condition que le bord entre eux ne soit pas "net".

Si le sommet d'un polygone voisin, opposé au bord commun, se trouve sur un bord pointu ou appartient au même groupe, alors ce polygone est ajouté au segment. Le processus est répété jusqu'à ce que tous les polygones de cette grille soient affichés. Voici à quoi ressemble le mécanisme de segmentation du maillage implémenté.


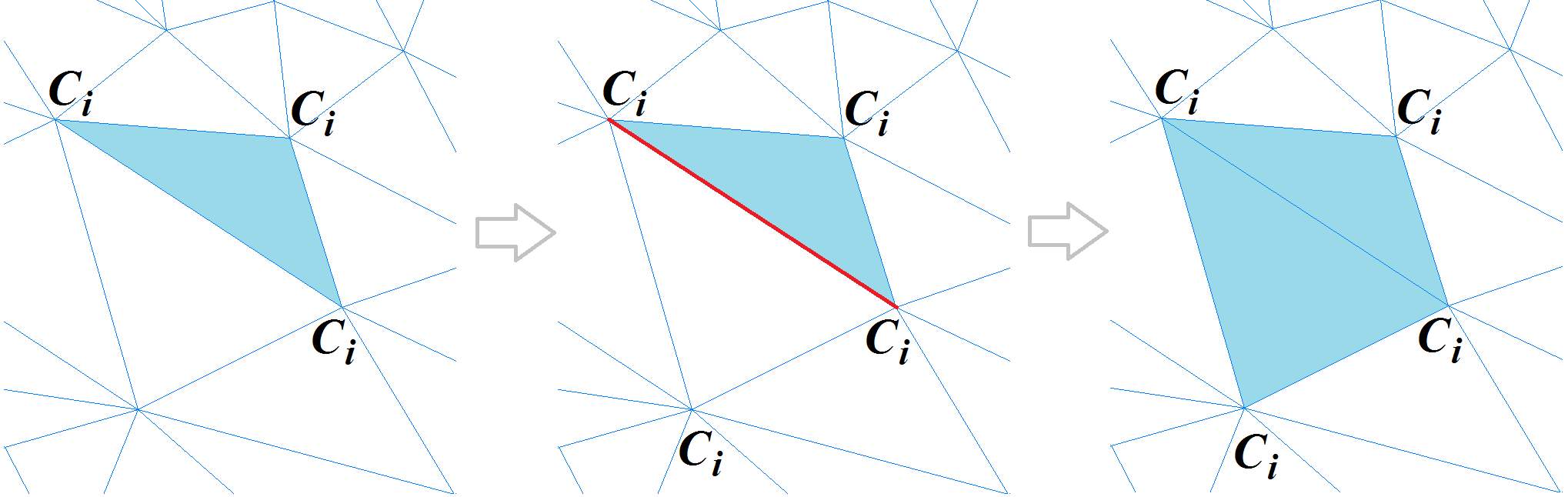Mécanisme de segmentation de maillage polygonal

À la fin de la procédure de formation des segments, un algorithme spécial pour assembler les segments adjacents est exécuté pour éliminer la segmentation excessive du maillage en question.

Reconnaissance de surface

Au deuxième stade, chacun des segments doit être associé à une certaine surface se rapprochant de sa forme avec une précision donnée. Tout d'abord, les valeurs des courbures principales pour un segment donné déterminent la possibilité de décrire la forme d'un segment par une surface élémentaire:

• avion: k ₁ = k ₂ = 0
• sphère: k ₁ = k ₂ = K > 0
• cylindre: k ₁ = K > 0, k ₂ = 0
• cône: k ₁ ∈ [ a , b ], k ₂ = 0
• tore: k ₁ = K , k ₂ ∈ [ a , b ]

Si aucune des surfaces élémentaires ne convient pour décrire un segment, l'algorithme essaiera de reconnaître la surface d'extrusion ou de rotation. En fin de compte, s'il n'était pas possible de sélectionner une surface analytique pour décrire la forme du segment, une surface NURBS sera construite pour cela.

Les surfaces élémentaires sont construites en utilisant des méthodes d'ajustement d'objets géométriques simples dans un ensemble de points. Ainsi, pour ajuster le cercle et la sphère, la méthode des moindres carrés est utilisée, pour ajuster le plan - la méthode du composant principal. Chaque surface reconstruite est vérifiée pour la conformité avec un segment pour une précision de reconnaissance donnée.

Pour plus de clarté, nous avons peint les surfaces reconnues de différentes couleurs: plans - bleu, cylindres - rouge, sphères - vert, cônes - jaune, tori - violet.


Maillage polygonal d'origine (gauche) et maillage segmenté (droite) avec des surfaces reconnues sur les segments

Création d'un modèle B-rep

La dernière étape de la transformation est la construction d'un modèle B-rep basé sur la segmentation des surfaces reconnues. Dans cette approche, un graphique des régions adjacentes est construit sur la base de régions segmentées, qui reflète la topologie du modèle et sert de base à la construction du modèle B-rep final.

Contrairement aux étapes précédentes de la conversion, l'assemblage B-rep est effectué dans un mode entièrement automatique: les lignes d'intersection des surfaces reconstruites adjacentes sont trouvées, les bords des faces sont construits dessus, les faces elles-mêmes et, enfin, la coque B-rep est assemblée.




Maillage polygonal d'origine (gauche) et modèle B-rep (droite)

Cependant, il n'est pas toujours possible de construire un shell topologiquement correct. À titre d'exemple d'une telle situation, supposons que pendant la reconstruction des surfaces, nous avons deux surfaces - un cylindre et un plan, et leur position dans l'espace est proche de la tangente. En raison d'erreurs dans la reconstruction des surfaces de leur intersection, il n'y en a peut-être pas du tout. Dans de tels cas, la coque peut être construite avec certains défauts que l'utilisateur peut corriger en ajustant correctement les paramètres de surface.

Types de modèles polygonaux et choix du mode de conversion

Aujourd'hui, il existe plusieurs sources principales de modèles dans la représentation polygonale:

• catalogues en ligne, bases de données de modèles 3D au format polygone (STL, VRML, OBJ), par exemple 3D Warehouse, Cults 3D, etc.
• Résultats de numérisation 3D
• résultats de l'optimisation du modèle topologique par les algorithmes CAE.

Les modèles polygonaux de ces sources peuvent être divisés en deux groupes: le premier comprend des modèles qui sont des triangulations d'objets B-rep, et le second - tous les autres. Les différences caractéristiques du premier groupe sont l'absence de bruit dans le maillage polygonal et la prédominance de surfaces définies analytiquement. Ainsi, la conversion aux modèles B-rep du premier groupe se fera soit en mode entièrement automatique soit avec une intervention minimale de l'utilisateur.

Les grilles polygonales des modèles du deuxième groupe impliquent une interaction interactive plus dense avec l'utilisateur. Par conséquent, nous avons initialement prévu deux modes de fonctionnement dans le C3D B-Shaper - entièrement automatique et interactif.

Le choix d'un mode particulier dépend également de la finalité de la transformation: dans certains cas, la connectivité topologique des éléments de la coque résultante, ainsi que sa justesse, peuvent être négligées. Une telle approche est acceptable, par exemple, pour optimiser le rendu dans une application BIM, lorsque l'utilisateur peut ajouter des éléments intérieurs arbitraires au modèle actuel de la pièce. D'autre part, pour les problèmes d'ingénierie inverse, il est nécessaire d'obtenir la copie la plus précise du modèle d'origine, par exemple, pour préserver l'alignement des cylindres avec une précision donnée, pour garantir l'emplacement tangent d'une paire de surfaces et, par conséquent, pour obtenir la topologie correcte du modèle - dans ce cas, vous ne pouvez pas vous passer de l'intervention de l'utilisateur dans processus de conversion.

L'interface de conversion automatique C3D B-Shaper est représentée par les fonctions suivantes, qui acceptent la grille d'entrée et les paramètres de conversion en entrée:

MbResultType ConvertMeshToShell( MbMesh & mesh, MbFaceShell *& shell, const MbMeshProcessorValues & params ); MbResultType ConvertCollectionToShell( MbCollection & collection, MbFaceShell *& shell, const MbMeshProcessorValues & params ); 

Les paramètres de conversion incluent la valeur de précision de reconnaissance, c.-à-d. la distance maximale autorisée des sommets du maillage polygonal dans les limites de ce segment à la surface reconnue. Cette précision peut être absolue ou relative: lors de l'utilisation de la précision relative, l'écart des faces du corps par rapport à la grille est vérifié par rapport à la taille du modèle.

De plus, l'utilisateur a la possibilité de changer de mode de reconnaissance, ce qui vous permet de contrôler les types de surfaces pendant la reconstruction.
Des capacités avancées de gestion des processus de segmentation et de reconnaissance de surface sont fournies par l'interface de classe MbMeshProcessor:

 class MbMeshProcessor { .. public: // “” . void SetUseMeshSmoothing( bool useSmoothing ); //   . const MbCollection & GetSegmentedMesh(); MbResultType SegmentMesh( bool createSurfaces = true ); void ResetSegmentation(); void UniteSegments( size_t firstSegmentIdx, size_t secondSegmentIdx ); MbResultType SegmentMeshBySeparators( const std::vector<std::vector<uint>> & sep ); //   . void FitSurfaceToSegment( size_t idxSegment ); void FitSurfaceToSegment( size_t idxSegment, MbeSpaceType surfaceType ); const MbSurface * GetSegmentSurface( size_t idxSegment ) const; //  B-rep . MbResultType CreateBRepShell( MbFaceShell *& pShell ); .. } 

Par exemple, pour corriger les résultats de la segmentation automatique, des outils sont fournis pour combiner les segments, les séparer, etc. L'utilisateur peut saisir une surface d'un type donné dans un segment, ainsi que modifier les paramètres d'une surface déjà reconnue.

Que se passe-t-il maintenant

En juillet, nous avons publié la première version du composant et continuons à présent de développer dans plusieurs domaines: algorithmes de segmentation automatique, outils d'édition de segmentation, construction de surfaces de forme libre (NURBS) basées sur un segment, et amélioration de la qualité de construction des shells B-rep.

Les développeurs intéressés peuvent tester le C3D B-Shaper. Le composant est fourni gratuitement pendant trois mois sur demande sur notre site Internet.

Auteur - Andrey Tumanin, Ph.D., mathématicien-programmeur de C3D Labs