
L'une des ressources les plus précieuses de tout réseau social est le «graphique des amitiés» - les informations sont diffusées via les connexions dans cette colonne, du contenu intéressant est envoyé aux utilisateurs et des commentaires constructifs sont envoyés aux auteurs de contenu. Dans le même temps, le graphique est également une source importante d'informations qui vous permet de mieux comprendre l'utilisateur et d'améliorer continuellement le service. Cependant, dans les cas où le graphique grandit, il est techniquement de plus en plus difficile d'en extraire des informations. Dans cet article, nous parlerons de quelques astuces utilisées pour traiter de grands graphiques dans OK.ru.
Pour commencer, considérez une tâche simple du monde réel: déterminer l'âge de l'utilisateur. La connaissance de l'âge permet au réseau social de sélectionner des contenus plus pertinents et de mieux s'adapter à la personne. Il semblerait que l'âge soit déjà indiqué lors de la création d'une page sur les réseaux sociaux, mais en fait, bien souvent, les utilisateurs sont rusés et indiquent un âge différent du réel. Un graphique social peut aider à rectifier la situation :).
Prenez, par exemple, Bob (tous les personnages de l'article sont fictifs, toute coïncidence avec la réalité est le résultat de la créativité d'une maison aléatoire):

D'une part, la moitié des amis de Bob sont des adolescents, ce qui suggère que Bob est aussi un adolescent. Mais il a aussi des amis plus âgés, donc la confiance dans la réponse est faible. Des informations supplémentaires provenant du graphique social peuvent aider à clarifier la réponse:

En tenant compte non seulement des arcs dans lesquels Bob est directement impliqué, mais aussi des arcs entre ses amis, nous pouvons voir que Bob fait partie d'une communauté dense d'adolescents, ce qui nous permet de tirer une conclusion sur son âge avec un plus grand degré de confiance.
Une telle structure de données est connue sous le nom de réseau ego ou sous-graphe ego; elle est utilisée depuis longtemps et a été utilisée avec succès pour résoudre de nombreux problèmes: recherche de communautés, identification de robots et de spam, recommandation d'amis et de contenu, etc. Cependant, le calcul de l'ego d'un sous-graphique pour tous les utilisateurs dans un graphique avec des centaines de millions de nœuds et des dizaines de milliards d'arcs se heurte à un certain nombre de "petites difficultés techniques" :).
Le problème principal est que lorsque l'on considère les informations sur la "deuxième étape" dans le graphique, une explosion quadratique du nombre de connexions se produit. Par exemple, pour un utilisateur avec 150 liens directs d'ego, un sous-graphique peut inclure jusqu'à  liens, et pour un utilisateur actif avec 5 000 amis, le sous-graphique ego peut atteindre plus de 12 000 000 de liens.
liens, et pour un utilisateur actif avec 5 000 amis, le sous-graphique ego peut atteindre plus de 12 000 000 de liens.
Une complication supplémentaire est le fait que le graphique est stocké dans un environnement distribué, et aucun nœud n'a une image complète du graphique en mémoire. Le travail sur le partitionnement équilibré des graphiques est effectué à la fois dans l'académie et dans l'industrie, mais même les meilleurs résultats lors de la collecte du sous-graphique de l'ego conduisent à une communication "tout le monde": pour obtenir des informations sur les amis des amis de l'utilisateur, vous devrez vous rendre dans toutes les "partitions" dans la plupart des cas.
L'une des alternatives de travail dans ce cas sera la duplication forcée des données (par exemple, l'algorithme 3 dans un article de Google ), mais cette duplication n'est pas non plus gratuite. Essayons de comprendre ce qui peut être amélioré dans ce processus.
Algorithme naïf
Pour commencer, considérons l'algorithme «naïf» pour générer un sous-graphique de l'ego:

L'algorithme suppose que le graphique d'origine est stocké sous forme de liste d'adjacence, c'est-à-dire Les informations sur tous les amis de l'utilisateur sont stockées dans un seul enregistrement avec l'ID utilisateur dans la clé et la liste des amis ID dans la valeur. Afin de prendre la deuxième étape et d'obtenir des informations sur les amis dont vous avez besoin:
- Convertissez un graphique en liste d'arêtes, où chaque arête est une entrée distincte.
- Rassemblez la liste des arêtes sur elle-même, ce qui donnera tous les chemins dans un graphique de longueur 2.
- Regroupez par début de chemin.
En sortie pour chaque utilisateur, nous obtenons des listes de chemins de longueur 2 pour chaque utilisateur. Il convient de noter ici que la structure résultante est en fait un voisinage en deux étapes de l'utilisateur , tandis que le sous-graphique ego est son sous-ensemble. Par conséquent, pour terminer le processus, nous devons filtrer tous les arcs qui sortent des amis immédiats.
Cet algorithme est bon car il est implémenté en deux lignes sur Scala sous Apache Spark . Mais les avantages s'arrêtent là: pour un graphique de taille industrielle, le volume de communication réseau est au-delà de la limite et la durée de fonctionnement est mesurée en jours. La principale difficulté est créée par deux opérations de mélange qui se produisent lorsque nous nous joignons et que nous nous regroupons. Est-il possible de réduire la quantité de données envoyées?
Sous-graphique de l'ego en un seul mélange
Étant donné que notre graphique des amitiés est symétrique, vous pouvez utiliser les optimisations proposées par Tomas Schank :
- Vous pouvez obtenir tous les chemins de longueur 2 sans rejoindre - si Bob a des amis Alice et Harry, il existe des chemins Alice-Bob-Harry et Harry-Bob-Alice.
- Lors du regroupement, deux chemins à l'entrée correspondent au même nouveau bord. Le chemin Bob-Alice-Dave et Bob-Dave-Alice contient les mêmes informations pour Bob, ce qui signifie que vous ne pouvez envoyer qu'un seul chemin sur deux, en triant les utilisateurs par leur ID.
Après avoir appliqué les optimisations, le schéma de travail ressemblera à ceci:

- Au premier stade de la génération, nous obtenons une liste de chemins de longueur 2 avec un filtre d'ordre ID.
- Le deuxième, nous nous regroupons par le premier utilisateur sur le chemin.
Dans ce paramètre, l'algorithme exécute une opération de lecture aléatoire et la taille des données transmises sur le réseau est divisée par deux. :)
Disposez le sous-graphique de l'ego en mémoire
Une question importante que nous n'avons pas encore examinée est de savoir comment décomposer les données dans l'ego d'un sous-graphique en mémoire. Pour stocker le graphique dans son ensemble, nous avons utilisé une liste d'adjacence. Cette structure est pratique pour les tâches où il est nécessaire de parcourir le graphique fini dans son ensemble, mais elle est coûteuse si nous voulons construire un graphique à partir de morceaux et faire des analyses plus subtiles. La structure idéale pour notre tâche doit effectuer efficacement les opérations suivantes:
- L'union de deux graphiques obtenus à partir de partitions différentes.
- Obtenir tous les amis humains.
- Vérifier si deux personnes sont connectées.
- Stockage en mémoire sans surcharge de boxe.
L'un des formats les plus adaptés à ces exigences est l'analogue d'une matrice CSR clairsemée :
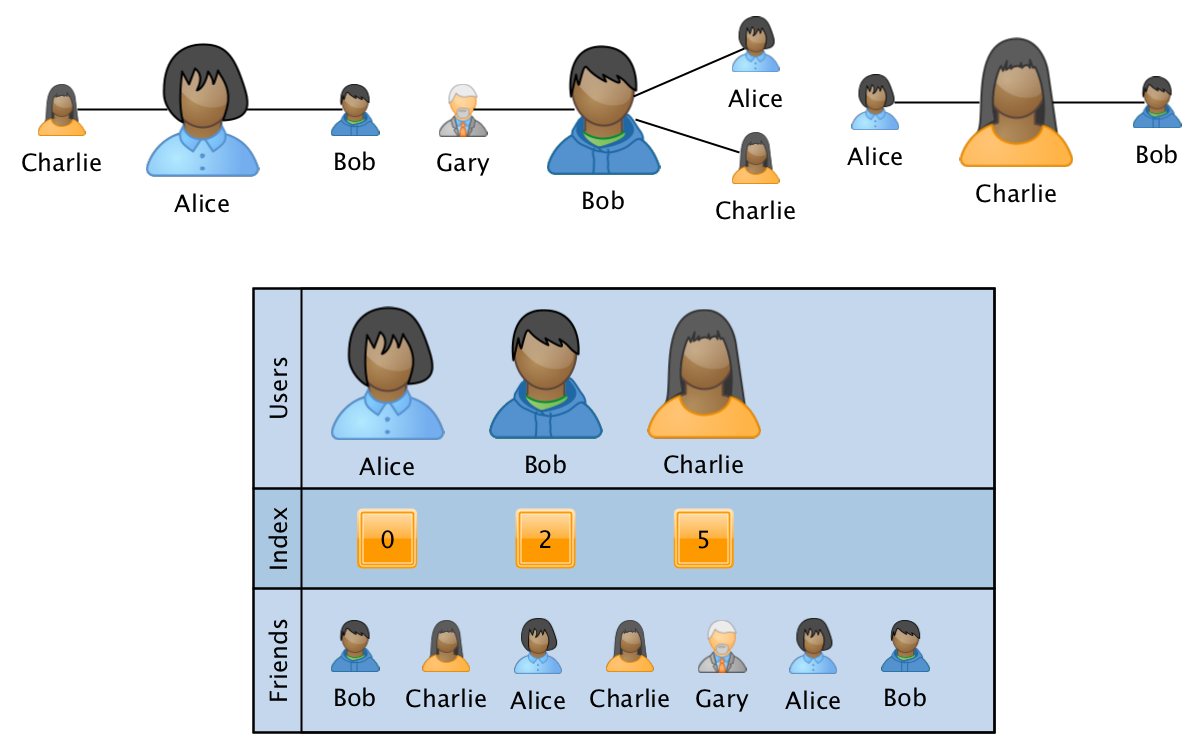
Dans ce cas, le graphique est stocké sous la forme de trois tableaux:
- utilisateurs - un tableau trié avec l'ID de tous les utilisateurs participant au graphique.
- index - un tableau de la même taille que les utilisateurs, où pour chaque utilisateur est stocké un pointeur d'index au début des informations sur les relations des utilisateurs dans le troisième tableau.
- friends - un tableau de taille égale au nombre d'arêtes dans le graphique, où les ID des utilisateurs liés sont affichés séquentiellement pour les ID correspondants des utilisateurs. Le tableau est trié pour la vitesse de traitement dans les informations sur les liens d'un seul utilisateur.
Dans ce format, l'opération de fusion de deux graphes est effectuée en temps linéaire, et l'opération d'obtention d'informations sur un utilisateur spécifique ou sur une paire d'utilisateurs par logarithme du nombre de sommets. Dans ce cas, la surcharge en mémoire ne dépend pas de la taille du graphique, car un nombre fixe de tableaux est utilisé. En ajoutant un quatrième tableau de données de taille égale à la taille des amis, vous pouvez enregistrer des informations supplémentaires associées aux relations dans le graphique.
En utilisant la propriété de symétrie du graphe, seule la moitié des arcs «triangulaires supérieurs» peut être stockée (lorsque les arcs sont stockés uniquement à partir d'un ID plus petit vers un ID plus grand), mais dans ce cas, la reconstruction de toutes les connexions d'un utilisateur individuel prendra un temps linéaire. Un bon compromis dans ce cas peut être une approche qui utilise un codage "triangulaire supérieur" pour le stockage et le transfert entre les nœuds, et un codage symétrique lors du chargement de l'ego du sous-graphique en mémoire pour l'analyse.
Réduisez le shuffle
Cependant, même après avoir implémenté toutes les optimisations mentionnées ci-dessus, la tâche de construction de tous les sous-graphiques de l'ego fonctionne toujours trop longtemps. Dans notre cas, environ 6 heures avec une utilisation élevée du cluster. Un examen plus approfondi montre que la principale source de complexité est toujours l'opération de lecture aléatoire, tandis qu'une partie importante des données impliquées dans la lecture aléatoire est rejetée dans les étapes suivantes. Le fait est que l'approche décrite crée un voisinage complet en deux étapes pour chaque utilisateur, tandis que le sous-graphique ego n'est qu'un sous-ensemble relativement petit de ce voisinage ne contenant que des arcs internes .
Par exemple, si, en traitant les voisins directs de Bob - Harry et Frank - nous savions qu'ils n'étaient pas amis l'un de l'autre, alors dès la première étape, nous pourrions filtrer ces chemins externes. Mais pour savoir pour tous Gary et Frenkov s'ils sont amis, vous devrez faire glisser le graphe d'amitié en mémoire à tous les nœuds de calcul ou effectuer des appels à distance tout en traitant chaque enregistrement, ce qui, selon les conditions de la tâche, est impossible.
Néanmoins, il existe une solution si nous nous permettons, dans un petit pourcentage de cas, de commettre des erreurs lorsque nous trouvons l'amitié là où elle n'existe pas. Il existe toute une famille de structures de données probabilistes qui permettent de réduire la consommation de mémoire lors du stockage de données par ordre de grandeur, tout en permettant une certaine quantité d'erreur. La structure la plus célèbre de ce type est le filtre Bloom , qui depuis de nombreuses années a été utilisé avec succès dans les bases de données industrielles pour compenser les échecs dans le cache "à longue queue".
La tâche principale du filtre Bloom est de répondre à la question "cet élément est-il inclus dans les nombreux éléments déjà vus?" De plus, si le filtre répond «non», alors l'élément n'est probablement pas inclus dans l'ensemble, mais s'il répond «oui» - il y a une faible probabilité que l'élément ne soit toujours pas là.
Dans notre cas, "l'élément" sera une paire d'utilisateurs, et "l'ensemble" sera tous les bords du graphique. Ensuite, le filtre Bloom peut être appliqué avec succès pour réduire la taille du shuffle:

Après avoir préparé le filtre Bloom à l'avance avec des informations sur le graphique, nous pouvons parcourir les amis de Harry pour découvrir que Bob et Ilona ne sont pas amis, ce qui signifie que nous n'avons pas besoin d'envoyer à Bob des informations sur la connexion entre Gary et Ilona. Cependant, les informations selon lesquelles Harry et Bob sont amis seuls devront toujours être envoyées afin que Bob puisse restaurer complètement son graphique d'amitié après le regroupement.
Supprimer le shuffle
Après avoir appliqué le filtre, la quantité de données envoyées est réduite d'environ 80% et la tâche se termine en 1 heure avec une charge de cluster modérée, vous permettant d'effectuer librement d'autres tâches en parallèle. Dans ce mode, il peut déjà être mis en service et mis en service au quotidien, mais il y a encore un potentiel d'optimisation.
Aussi paradoxal que cela puisse paraître, le problème peut être résolu sans recourir à la lecture aléatoire, si vous vous permettez un certain pourcentage d'erreurs. Et le filtre Bloom peut nous aider avec ceci:

Si vous parcourez la liste d'amis de Bob à l'aide d'un filtre, nous découvrons qu'Alice et Charlie sont presque certainement amis, nous pouvons immédiatement ajouter l'arc correspondant au sous-graphique de l'ego de Bob. Dans ce cas, l'ensemble du processus prendra moins de 15 minutes et ne nécessitera pas de transfert de données sur le réseau, cependant, un certain pourcentage d'arcs, en fonction des paramètres de filtre, peut être absent dans la réalité.
Les arcs supplémentaires ajoutés par le filtre n'introduisent pas de distorsions significatives pour certaines tâches: par exemple, lors du comptage de triangles, nous pouvons facilement corriger le résultat, et lors de la préparation des attributs pour les algorithmes d'apprentissage automatique, la correction ML elle-même peut être apprise à l'étape suivante.
Mais dans certaines tâches, des arcs supplémentaires entraînent une détérioration fatale de la qualité du résultat: par exemple, lors de la recherche de composants connectés dans le sous-graphique de l'ego avec un ego distant (sans le sommet de l'utilisateur), la probabilité d'un «pont fantôme» entre les composants augmente de façon quadratique par rapport à leur taille, ce qui conduit à que presque partout nous obtenons un gros composant.
Il existe également une zone intermédiaire où l'effet négatif des arcs supplémentaires doit être évalué expérimentalement: par exemple, certains algorithmes de recherche de communauté peuvent assez bien gérer un peu de bruit, renvoyant une structure de communauté presque identique.
Au lieu d'une conclusion
Les sous-graphiques des utilisateurs d'Ego sont une source importante d'informations activement utilisée dans OK pour améliorer la qualité des recommandations, affiner les données démographiques et lutter contre le spam, mais leur calcul est semé d'embûches.
Dans l'article, nous avons examiné l'évolution de l'approche de la tâche de construction de sous-graphiques de l'ego pour tous les utilisateurs d'un réseau social et avons pu améliorer le temps de travail des 20 heures initiales à 1 heure, et dans le cas d'un petit pourcentage d'erreurs, jusqu'à 10-15 minutes.
Les trois «piliers» sur lesquels repose la décision finale sont:
- Utilisation de la propriété de symétrie du graphe et des algorithmes Tomas Schank .
- Stockez efficacement les sous-graphiques de l'ego à l'aide d'une matrice CSR clairsemée .
- Utilisez un filtre Bloom pour réduire le transfert de données sur le réseau.
Des exemples de l'évolution du code de l'algorithme peuvent être trouvés dans le cahier Zeppelin .