Croissance. Poids. Trois voisins

À la recherche d'un DataSet intéressant et simple, je suis tombé sur ce bel homme .

À propos de cette beauté

Il contient des données sur la croissance et le poids de 10 000 hommes et femmes . Pas de description. Rien de "superflu". Seuls la hauteur, le poids et la marque au sol. J'ai aimé cette mystérieuse simplicité.

Eh bien, commençons!

Qu'est-ce qui m'intéressait?

• Quelle est la plage de poids et de taille pour la plupart des hommes et des femmes?
• Quel genre d' homme et de femme «moyenne» sont-ils?
• Le modèle d'apprentissage automatique KNN simple à partir de ces données peut-il prédire le poids en fonction de la taille ?

C'est parti!

Premier coup d'oeil

Tout d'abord, chargez les modules nécessaires

#      import pandas as pd #     import matplotlib.pyplot as plt %matplotlib inline #    «  » from sklearn.neighbors import KNeighborsRegressor #         from sklearn.model_selection import train_test_split 

Lorsque les bibliothèques se sont levées exactement - il était temps de charger le DataSet lui-même et d'examiner les 10 premiers éléments. Cela est nécessaire pour que notre intestin soit calme, que nous ayons tout chargé correctement.

Soit dit en passant, ne vous inquiétez pas que la taille et le poids diffèrent de ce à quoi nous sommes habitués. Cela est dû à un système de mesure différent: les pouces et les livres , au lieu des centimètres et des kilogrammes .

 data = pd.read_csv('weight-height.csv') data.head(10) 

Bon! On voit que les dix premières entrées sont des «hommes». On voit leur taille et leur poids . Les données sont bien chargées.

Vous pouvez maintenant regarder le nombre de lignes de l'ensemble.

 data.shape >> (10000, 3) 

Dix mille lignes / enregistrements. Et chacun a trois paramètres . Ce dont vous avez besoin!

Il est temps de réparer le système de mesure. Maintenant, voici les centimètres et les kilogrammes.

 data['Height'] *= 2.54 data['Weight'] /= 2.205 #    data.head(10) 

Maintenant, il est devenu plus familier. Et le tout premier enregistrement nous parle d'un homme avec une taille de ~ 190cm et un poids de ~ 110kg. Grand homme. Appelons-le Bob.

Mais comment comprendre: est-ce beaucoup ou un peu par rapport au reste? Est-il possible que nous soyons tous des haricots plus ou moins? C'est un peu plus tard.

Voyons maintenant à quel point les deux sexes sont symétriques dans cet ensemble de données?

 data['Gender'].value_counts() >> Male 5000 Female 5000 Name: Gender, dtype: int64 

Idéalement également divisé. Et c'est bien, car s'il y avait: 9 999 hommes et 1 femme, il serait insensé de prétendre que ce DataSet révèle également les deux sexes. Dans notre cas, tout va bien!

Divisez et apprenez!

Maintenant, l'intuition suggère qu'il sera correct de séparer les deux sexes et d'explorer séparément. En effet, dans la vie, nous voyons souvent que les hommes et les femmes ont plus ou moins une taille et un poids différents

 #  data_male = data[data['Gender'] == 'Male'].copy() #  data_female = data[data['Gender'] == 'Female'].copy() 

Jetons un coup d'œil aux petites statistiques descriptives que le module pandas nous offre.

Hommes :

 data_male.describe() 

Femmes :

 data_female.describe() 

On voit que chez les hommes la moyenne et la médiane sont de 175cm et 85kg. Et chez la femme : 162cm et 62kg. Cela nous indique qu'il n'y a pas de fortes émissions. Ou ils sont symétriques des deux côtés de la médiane. Ce qui est très rare.

Mais les deux sexes ont de légers écarts de la moyenne par rapport à la médiane. Mais ils sont insignifiants et ils ne sont visibles qu'aux centièmes. Continuons!

Histogramme

Il s'agit d'un graphique qui trace les valeurs du minimum au maximum par ordre de croissance et montre le nombre d'instances individuelles.

 fig, axes = plt.subplots(2,2, figsize=(20,10)) plt.subplots_adjust(wspace=0, hspace=0) axes[0,0].hist(data_male['Height'], label='Male Height', bins=100, color='red') axes[0,1].hist(data_male['Weight'], label='Male Weight', bins=100, color='red', alpha=0.4) axes[1,0].hist(data_female['Height'], label='Female Height', bins=100, color='blue') axes[1,1].hist(data_female['Weight'], label='Female Weight', bins=100, color='blue', alpha=0.4) axes[0,0].legend(loc=2, fontsize=20) axes[0,1].legend(loc=2, fontsize=20) axes[1,0].legend(loc=2, fontsize=20) axes[1,1].legend(loc=2, fontsize=20) plt.savefig('plt_histogram.png') plt.show() 

Les données sont distribuées en forme de cloche. Très similaire à la distribution normale .

En plus des tests statistiques de distribution normale, il existe un test visuel. Si la distribution par type et logique semble être normale - nous pouvons supposer avec certaines hypothèses que nous y faisons face.

On pourrait faire un test de normalité statistique et déterminer la valeur de p, mais Je ne peux pas cela dépasse le cadre de l'article.

Apprendre à travailler avec des stylos

Les pandas peuvent compter beaucoup pour nous. Mais vous devez vous-même compter au moins une fois quelques statistiques. Je vais maintenant montrer comment calculer l'écart type .

Faisons-le sur l'exemple des hommes et la caractéristique - la croissance.

Moyenne

Formule

$$

$$M = \ frac {1} {N} \ sum \ limits_ {i = 1} ^ N n_i$$

où

• M - valeur moyenne
• N est le nombre d'instances
• ni - instance unique

Code:

 mean = data_male['Height'].mean() print('mean:\t{:.2f}'.format(mean)) >> mean: 175.33 

Hauteur moyenne - 175cm

Déviation au carré

$$

$$d_i = (n_i - M) ^ 2$$

où

• di - écart unique
• ni - instance unique
• M - moyen

Code:

 data_male['Height_d'] = (data_male['Height'] - mean) ** 2 data_male['Height_d'].head(10) >> 0 149.927893 1 0.385495 2 166.739089 3 47.193692 4 4.721246 5 20.288347 6 0.375539 7 2.964214 8 25.997623 9 200.149603 Name: Height_d, dtype: float64 

Dispersion

Formule

$$

$$D = \ frac {1} {N} \ sum \ limits_ {i = 1} ^ N d_i$$

où

• D est la valeur de dispersion
• di - écart unique
• N est le nombre d'instances

Code:

 disp = data_male['Height_d'].mean() print('disp:\t{:.2f}'.format(disp)) >> disp: 52.89 

Dispersion - 53

Écart type

Formule

$$

$$std = \ sqrt {D}$$

où

• std - valeur d'écart type
• D est la valeur de dispersion

Code:

 std = disp ** 0.5 print('std:\t{:.2f}'.format(std)) >> std: 7.27 

Écart type - 7

Intervalles de confiance

Nous allons maintenant découvrir dans quelles gammes de croissance et de poids se situent 68%, 95% et 99,7% des hommes et des femmes .

Ce n'est pas si difficile - vous devez ajouter et soustraire l' écart-type de la moyenne. Cela ressemble à ceci:

• 68% - plus ou moins un écart-type
• 95% - plus ou moins deux écarts-types
• 99,7% - plus ou moins trois écarts-types

Nous écrivons une fonction auxiliaire qui tiendra compte de ceci:

 def get_stats(series, title='noname'): #    print('= {} =\n'.format(title.upper())) #     pandas descr = series.describe() #   mean = descr['mean'] print('= Mean:\t{:.0f}'.format(mean)) #    std = descr['std'] print('= Std:\t{:.0f}'.format(std)) #    print('\n= = = =\n') #   ## 68% devi_1 = [mean - std, mean + std] ## 95% devi_2 = [mean - 2 * std, mean + 2 * std] ## 99.7% devi_3 = [mean - 3 * std, mean + 3 * std] #   print('= 68% is from\t\t{:.0f} to {:.0f}'.format(devi_1[0], devi_1[1])) print('= 95% is from\t\t{:.0f} to {:.0f}'.format(devi_2[0], devi_2[1])) print('= 99.7% is from\t\t{:.0f} to {:.0f}'.format(devi_3[0], devi_3[1])) 

Eh bien, appliquez-le aux données:

Hommes | Croissance

 get_stats(data_male['Height'], title='Male Height') >> = MALE HEIGHT = = Mean: 175 = Std: 7 = = = = = 68% is from 168 to 183 = 95% is from 161 to 190 = 99.7% is from 154 to 197 

Hommes | Le poids

 get_stats(data_male['Height'], title='Male Height') >> = MALE WEIGHT = = Mean: 85 = Std: 9 = = = = = 68% is from 76 to 94 = 95% is from 67 to 103 = 99.7% is from 58 to 112 

Femmes | Croissance

 get_stats(data_male['Height'], title='Male Height') >> = FEMALE HEIGHT = = Mean: 162 = Std: 7 = = = = = 68% is from 155 to 169 = 95% is from 148 to 176 = 99.7% is from 141 to 182 

Femmes | Le poids

 get_stats(data_male['Height'], title='Male Height') >> = FEMALE WEIGHT = = Mean: 62 = Std: 9 = = = = = 68% is from 53 to 70 = 95% is from 44 to 79 = 99.7% is from 36 to 87 

D'où les conclusions:

• La plupart des hommes: 154 cm - 197 cm et 58 kg - 112 kg.
• La plupart des femmes: 141 cm - 182 cm et 36 kg - 87 kg.

Maintenant, il ne reste plus qu'à appliquer l'apprentissage automatique à cet ensemble et à essayer de prédire le poids en fonction de la taille.

Voisins les plus proches

L'algorithme "Aux voisins les plus proches" est simple. Il existe pour les tâches de classification - pour distinguer un chat d'un chien - et pour les tâches de régression - pour deviner le poids en fonction de la taille. Voilà ce dont nous avons besoin!

Pour la régression, il utilise l'algorithme suivant:

• Se souvient de tous les points de données
• Lorsqu'un nouveau point apparaît, il recherche K ses voisins les plus proches (le nombre K est fixé par l'utilisateur)
• Moyenne du résultat
• Donne une réponse

Vous devez d'abord diviser l'ensemble de données en parties de formation et de test et tester l'algorithme

Expérimenter sur les hommes

 X_train, X_test, y_train, y_test = train_test_split(data_male['Height'], data_male['Weight']) 

Divisé, il est temps d'essayer.

 #   knr3 = KNeighborsRegressor(n_neighbors=3) knr3.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr3.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.8298400793623182 #   knr5 = KNeighborsRegressor(n_neighbors=5) knr5.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr5.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.7958051642678619 #   knr7 = KNeighborsRegressor(n_neighbors=7) knr7.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr7.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.7769249318420969 

Nous n'irons pas loin et nous arrêterons à trois voisins. Mais la question est: un tel modèle peut-il deviner mon poids?

 knr3.predict([[180]])[0, 0] >> 88.67596236265881 

88kg est très proche. Cette seconde, mon poids est de 89,8 kg

Tableau de prédiction pour les hommes

Le temps de construire ma partie préférée de la science est le graphisme.

 array_male = [] #   99.7% xaxis = range(154, 198) for h in xaxis: ans = knr3.predict([[h]]) array_male.append(ans[0, 0]) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_male, 'r-', linewidth=4) plt.title('Male heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_male.png') plt.show() 

Modèle et tableau de prédiction pour les femmes

 X_train, X_test, y_train, y_test = train_test_split(data_female['Height'], data_female['Weight']) knr3 = KNeighborsRegressor(n_neighbors=3) knr3.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr3.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.8135681584074799 

 array_female = [] #   99.7% xaxis = range(141, 183) for h in xaxis: ans = knr3.predict([[h]]) array_female.append(ans[0, 0]) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_female, 'b-', linewidth=4) plt.title('Female heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_female.png') plt.show() 

Et bien sûr, il est intéressant de voir comment ces graphiques se ressemblent:

 #      xaxis = range(154, 183) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_male[:-15], 'r-', linewidth=4) plt.plot(xaxis, array_female[13:], 'b-', linewidth=4) plt.title('Together heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_together.png') plt.show() 

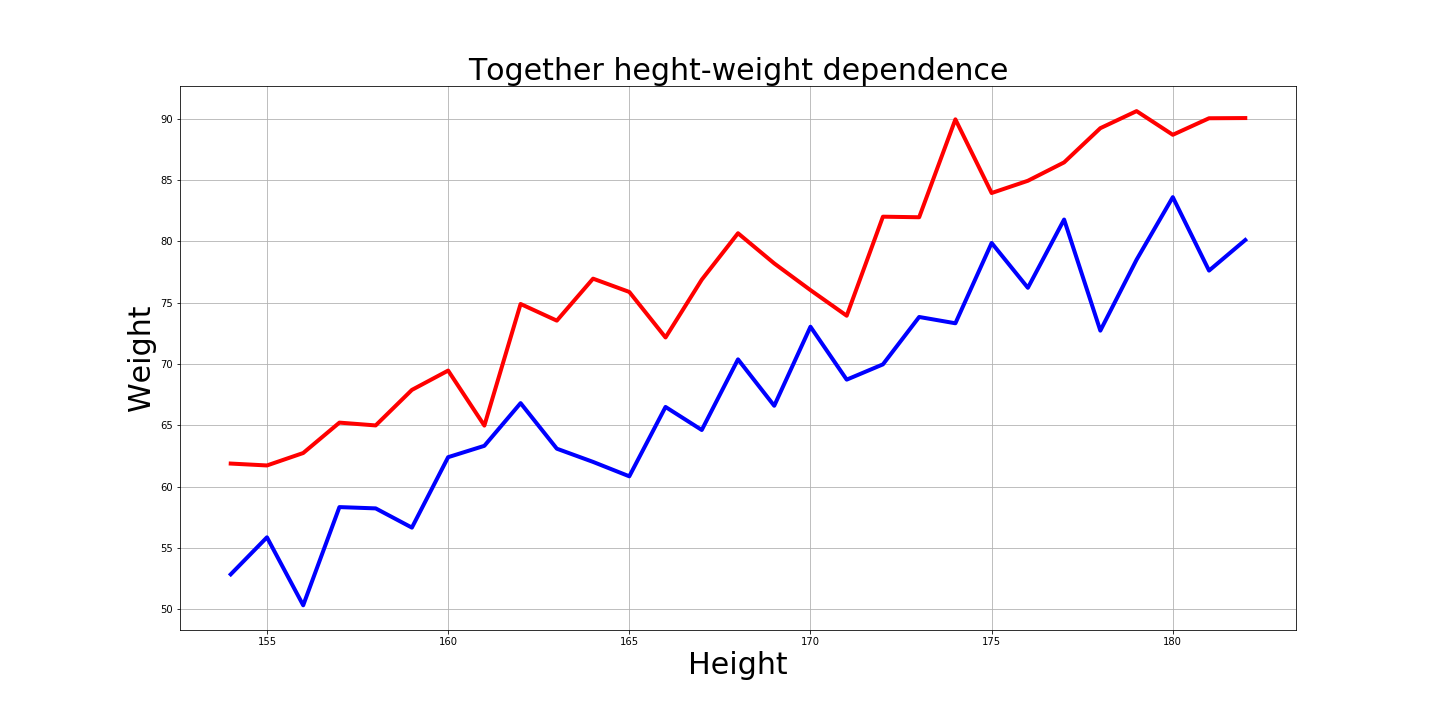
Réponses aux questions

- Quelle est la plage de poids et de taille pour la plupart des hommes et des femmes?

99,7% des hommes: de 154 cm à 197 cm et de 58 kg à 112 kg.
Et 99,7% des femmes: de 141cm à 182cm et de 36kg à 87kg.

- De quel type d'homme et de femme «moyenne» s'agit-il?

L'homme moyen mesure 175 cm et 85 kg.
Et la femme moyenne mesure 162 cm et 62 kg.

- Le modèle d'apprentissage automatique KNN simple à partir de ces données prédira-t-il le poids en fonction de la taille?

Oui, le modèle prédit 88 kg et j'en ai 89,8 kg.

Tout ce que j'ai fait, je l'ai récupéré ici

Inconvénients de l'article

• Il n'y a aucune description de DataSet. Probablement, l'âge et d'autres facteurs chez les personnes étaient différents. Par conséquent, on ne peut pas l'accepter sur la foi, mais pour le plaisir de l'expérience - s'il vous plaît.
• Dans le bon sens - il fallait faire un test de normalité de distribution

Épilogue

Comme si vous atteigniez l'intervalle de 99,7%