Algorithmes de traitement de chaîne intelligents dans ClickHouse

ClickHouse rencontre constamment des tâches de traitement de chaîne. Par exemple, rechercher, calculer les propriétés des chaînes UTF-8, ou quelque chose de plus exotique, qu'il s'agisse d'une recherche sensible à la casse ou d'une recherche de données compressées.

Tout a commencé avec le fait que la responsable du développement de ClickHouse, Lesha Milovidov o6CuFl2Q, est venue nous voir à la Faculté d'informatique de la Higher School of Economics et a proposé un grand nombre de sujets pour des articles et des diplômes. Quand j'ai vu «Smart String Processing Algorithms in ClickHouse» (moi, une personne qui s'intéresse à divers algorithmes, y compris expérimentaux), j'ai immédiatement mis en place des plans sur la façon de faire le diplôme le plus cool. Ma joie et mon expression peuvent être décrites comme suit:

Clickhouse

ClickHouse a soigneusement réfléchi à l'organisation du stockage des données en mémoire - en colonnes. À la fin de chaque colonne, il y a un remplissage de 15 octets pour une lecture sûre d'un registre de 16 octets. Par exemple, ColumnString stocke des chaînes terminées nulles avec des décalages. Il est très pratique de travailler avec de tels tableaux.

Il existe également ColumnFixedString, ColumnConst et LowCardinality, mais nous n'en parlerons pas en détail aujourd'hui. Le point principal à ce stade est que la conception de la lecture sûre des queues est très bien, et la localité des données joue également un rôle dans le traitement.

Recherche de sous-chaîne

Très probablement, vous connaissez de nombreux algorithmes différents pour trouver une sous-chaîne dans une chaîne. Nous parlerons de ceux qui sont utilisés dans ClickHouse. Nous introduisons d'abord quelques définitions:

1. meule de foin - la ligne dans laquelle nous regardons; généralement, la longueur est désignée par n .
2. aiguille - la chaîne ou l'expression régulière que nous recherchons; la longueur sera notée m .

Après avoir étudié un grand nombre d'algorithmes, je peux dire qu'il existe 2 (maximum 3) types d'algorithmes de recherche de sous-chaîne. Le premier est la création sous une forme ou une autre de structures de suffixes. Le deuxième type est constitué d'algorithmes basés sur la comparaison de mémoire. Il existe également l'algorithme Rabin-Karp, qui utilise des hachages, mais il est assez unique en son genre. L'algorithme le plus rapide n'existe pas, tout dépend de la taille de l'alphabet, de la longueur de l'aiguille, de la botte de foin et de la fréquence d'occurrence.

Découvrez les différents algorithmes ici . Et voici les algorithmes les plus populaires:

1. Knut - Morris - Pratt,
2. Boyer - Moore,
3. Boyer - Moore - Horspool,
4. Rabin - Carpe,
5. Double face (utilisé dans la glibc appelée «memmem»),
6. BNDM

La liste continue. Chez ClickHouse, nous avons honnêtement tout essayé, mais nous avons finalement opté pour une version plus extraordinaire.

Algorithme de Volnitsky

L'algorithme a été publié sur le blog du programmeur Leonid Volnitsky fin 2010. Il rappelle quelque peu l'algorithme de Boyer-Moore-Horspool, seulement une version améliorée.

Si m <4 , alors l'algorithme de recherche standard est utilisé. Enregistrer toutes les aiguilles bigrammes (2 octets consécutifs) de la fin dans une table de hachage avec un adressage ouvert de taille | Sigma | ² éléments (en pratique, ce sont 2 ¹⁶ éléments), où les décalages de ce bigramme seront les valeurs, et le bigramme lui-même sera le hachage et l'index en même temps. La position initiale sera à la position m - 2 depuis le début de la meule de foin. Nous suivons la meule de foin à l'étape m - 1 , regardons le prochain bigramme de cette position dans la meule de foin et considérons toutes les valeurs du bigramme dans la table de hachage. Ensuite, nous comparerons deux morceaux de mémoire avec l'algorithme de comparaison habituel. La queue qui reste sera traitée par le même algorithme.

L'étape m-1 est choisie de telle manière que s'il y a une occurrence d'aiguille dans une botte de foin, alors nous considérerons certainement le bigramme de cette entrée - garantissant ainsi que nous retournons la position de l'entrée dans la botte de foin. La première occurrence est garantie par le fait que nous ajoutons des index de la fin à la table de hachage par bigram. Cela signifie que lorsque nous allons de gauche à droite, nous considérerons d'abord les bigrammes à partir de la fin de la ligne (peut-être en considérant initialement des bigrammes complètement inutiles), puis plus près du début.

Prenons un exemple. Que la botte de foin en ficelle soit abacabaac et aiguille égale à aaca . La table de hachage sera {aa : 0, ac : 1, ca : 2} .

 0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -    

Nous voyons le bigram ac . En aiguille c'est, on substitue en égalité:

 0 1 2 3 4 5 6 7 8 9 abacabaaca aaca 

Ne correspondait pas. Après ac il n'y a pas d'entrées dans la table de hachage, nous passons à l'étape 3:

 0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -    

Il n'y a pas de bigrammes ba dans la table de hachage, allez-y:

 0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -    

Il y a un bigramme dans l'aiguille, on regarde le décalage et on trouve l'entrée:

 0 1 2 3 4 5 6 7 8 9 abacabaaca aaca 

L'algorithme présente de nombreux avantages. Tout d'abord, vous n'avez pas besoin d'allouer de mémoire sur le tas, et 64 Ko sur la pile ne sont pas quelque chose de transcendantal maintenant. Deuxièmement, 2 ¹⁶ est un excellent nombre pour prendre le modulo pour le processeur; ce ne sont que des instructions movzwl (ou, comme nous plaisantons, «movsvl») et la famille.

En moyenne, cet algorithme s'est avéré le meilleur. Nous avons pris les données de Yandex.Metrica, les demandes sont presque réelles. Une vitesse de flux, plus c'est mieux, KMP: algorithme Knut - Morris - Pratt, BM: Boyer - Moore, BMH: Boyer - Moore - Horspool.

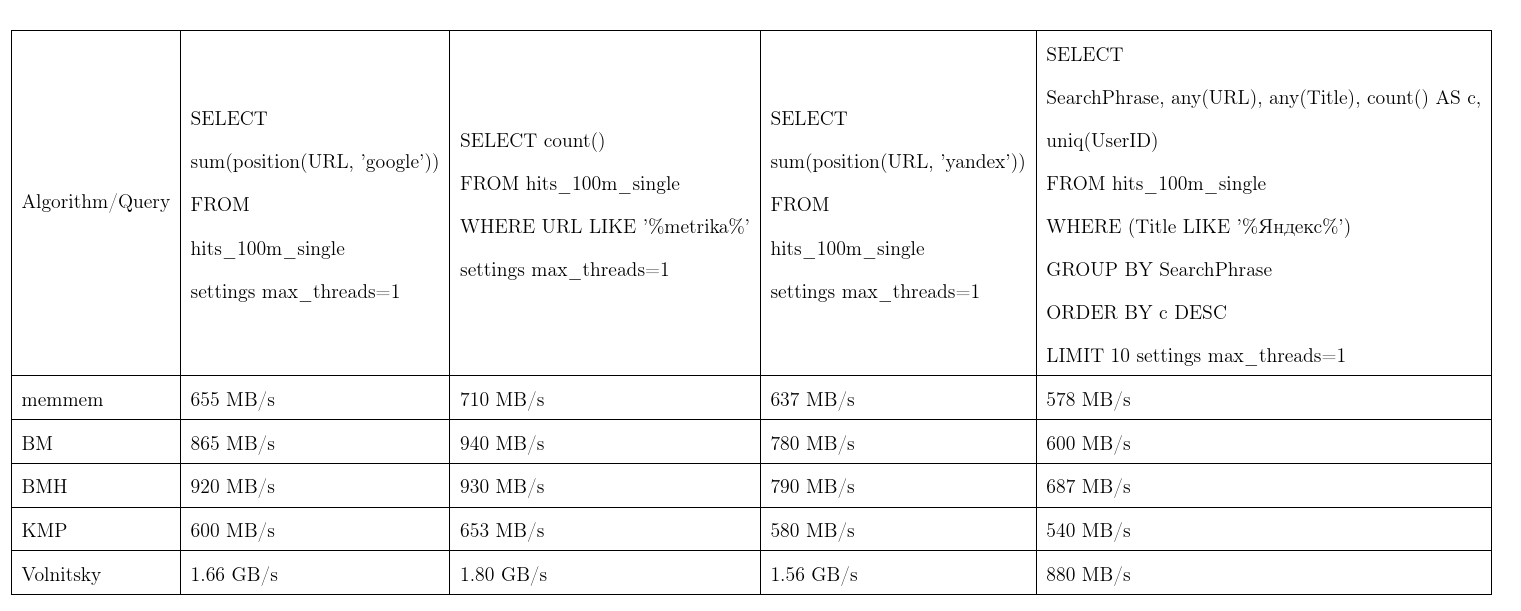
Pour ne pas être infondé, l'algorithme peut travailler le temps quadratique:

Il est utilisé dans la fonction de position(Column, ConstNeedle) et agit également comme une optimisation pour les recherches d'expressions régulières.

Recherche d'expression régulière

Nous vous expliquerons comment ClickHouse optimise les recherches d'expressions régulières. De nombreuses expressions régulières contiennent une sous-chaîne à l'intérieur, qui doit être à l'intérieur d'une botte de foin. Afin de ne pas construire une machine à états finis et de la comparer, nous isolerons de telles sous-chaînes.

Pour ce faire, c'est assez simple: tout crochet ouvrant augmente le niveau d'imbrication, tout crochet fermant diminue; il existe également des caractères spécifiques aux expressions régulières (par exemple, '.', '*', '?', '\ w', etc.). Nous devons obtenir toutes les sous-chaînes au niveau 0. Prenons un exemple:

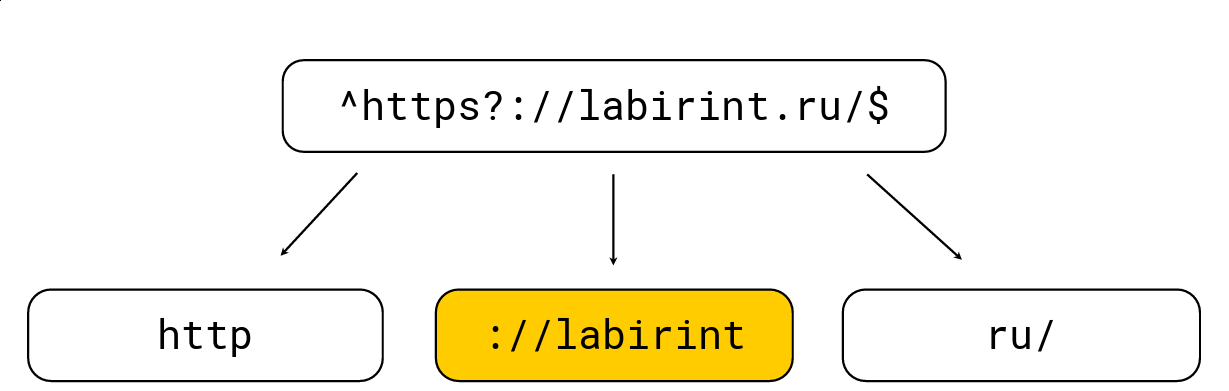
Nous le décomposons en ces sous-chaînes qui doivent être dans la botte de foin de l'expression régulière, après quoi nous sélectionnons la longueur maximale, recherchons des candidats dessus, puis vérifions avec le moteur d'expression régulière habituel RE2. Dans l'image ci-dessus, il y a une expression régulière, elle est traitée par le moteur RE2 habituel à 736 Mo / s, Hyperscan (à ce sujet un peu plus tard) gère à 1,6 Go / s, et nous gérons 1,69 Go / s par cœur avec décompression LZ4. En général, une telle optimisation est en surface et accélère considérablement la recherche d'expressions régulières, mais souvent elle n'est pas implémentée dans les outils, ce qui m'étonne beaucoup.

Le mot clé LIKE est également optimisé à l'aide de cet algorithme, seulement après que LIKE peut qu'une expression régulière très simplifiée passe par %%%%% (sous-chaîne arbitraire) et _ (caractère arbitraire).

Malheureusement, toutes les expressions régulières ne sont pas soumises à de telles optimisations, par exemple, à partir de yandex|google il est impossible d'extraire explicitement des sous-chaînes qui doivent apparaître dans une botte de foin. Par conséquent, nous avons trouvé une solution complètement différente.

Rechercher de nombreuses sous-chaînes

Le problème est qu'il y a beaucoup d'aiguilles, et je veux comprendre si au moins l'une d'entre elles est incluse dans la botte de foin. Il existe des méthodes assez classiques pour une telle recherche, par exemple l'algorithme Aho-Korasik. Mais il n'a pas été trop rapide pour notre tâche. Nous en reparlerons un peu plus tard.

Lesha ClickHouse aime les solutions non standard, nous avons donc décidé d'essayer quelque chose de différent et, peut-être, de créer nous-mêmes un nouvel algorithme de recherche. Et ils l'ont fait.

Nous avons examiné l'algorithme de Volnitsky et l'avons modifié pour qu'il commence à rechercher de nombreuses sous-chaînes à la fois. Pour ce faire, il vous suffit d'ajouter les bigrammes de toutes les lignes et de stocker en plus un index de ligne dans la table de hachage. L'étape sera sélectionnée parmi au moins toutes les longueurs d'aiguille moins 1 pour garantir à nouveau la propriété que s'il y a une occurrence, nous verrons son bigramme. La table de hachage passera à 128 Ko (les lignes de plus de 255 sont traitées par l'algorithme standard, nous ne considérerons pas plus de 256 aiguilles). Je suis très paresseux, alors voici un exemple de la présentation (lu de gauche à droite de haut en bas):

Nous avons commencé à regarder comment un tel algorithme se comporte par rapport aux autres (les lignes sont tirées de données réelles). Et pour un petit nombre de lignes, il fait tout (la vitesse avec déchargement est indiquée - environ 2,5 Go / s).

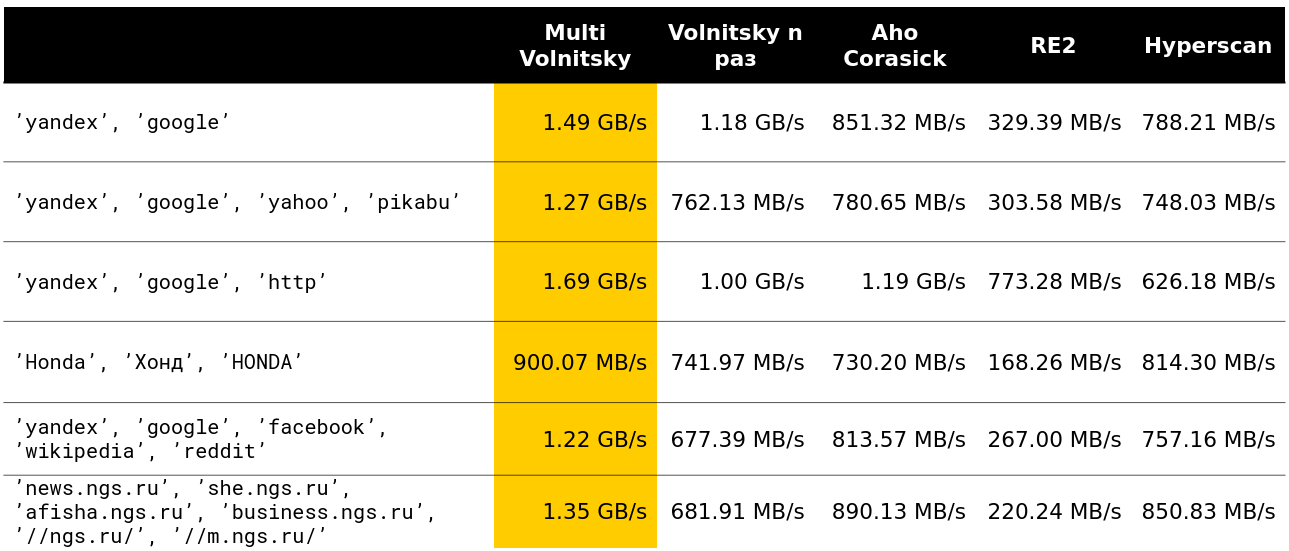
Puis c'est devenu intéressant. Par exemple, avec un grand nombre de bigrammes similaires, nous perdons face à certains concurrents. C'est compréhensible - nous commençons à comparer de nombreux morceaux de mémoire et à nous dégrader.

Vous ne pouvez pas accélérer beaucoup si la longueur minimale de l'aiguille est suffisamment grande. De toute évidence, nous avons plus d'occasions de sauter des morceaux entiers de meule de foin sans rien payer pour cela.

Le point de basculement commence quelque part sur les lignes 13 à 15. Environ 97% des demandes que j'ai vues sur le cluster étaient inférieures à 15 lignes:

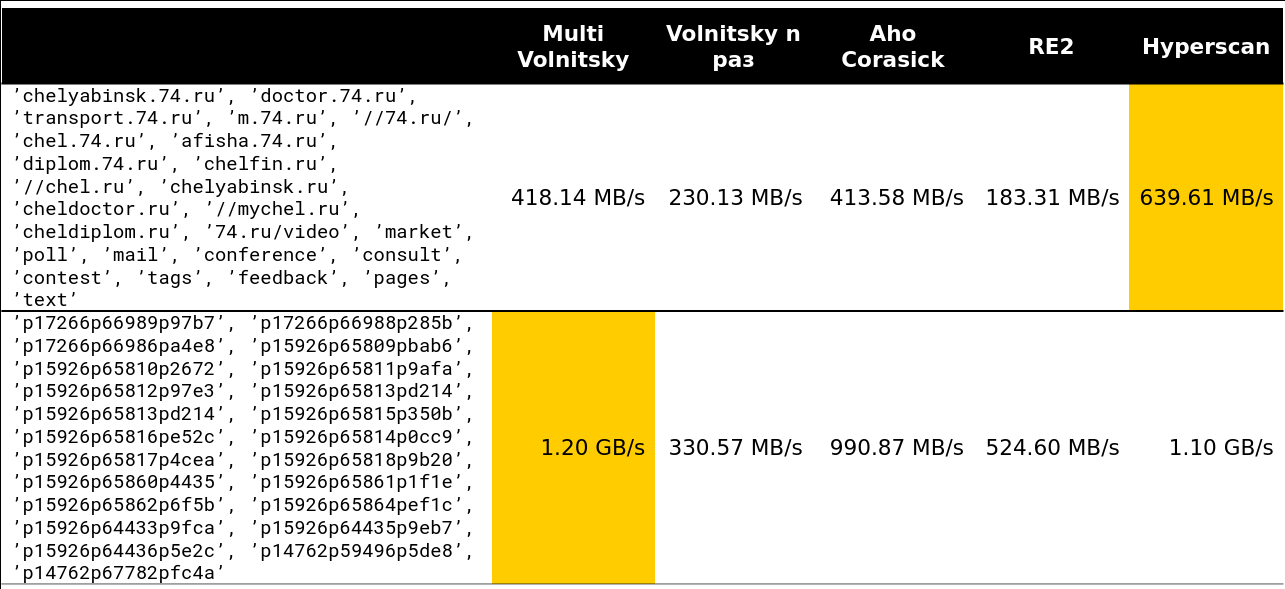
Eh bien, une image très effrayante - 41 lignes, de nombreux bigrammes répétitifs:

En conséquence, dans ClickHouse (19.5), nous avons implémenté les fonctions suivantes via cet algorithme:

- multiSearchAny(h, [n_1, ..., n_k]) - 1, si au moins une des aiguilles se trouve dans la botte de foin.
- multiSearchFirstPosition(h, [n_1, ..., n_k]) - la position la plus à gauche de l'entrée dans la botte de foin (à partir d'une) ou 0 si elle n'est pas trouvée.
- multiSearchFirstIndex(h, [n_1, ..., n_k]) - l'index d'aiguille le plus à gauche, qui a été trouvé dans la botte de foin; 0 s'il n'est pas trouvé.
- multiSearchAllPositions(h, [n_1, ..., n_k]) - toutes les premières positions de toutes les aiguilles, renvoie un tableau.

Les suffixes sont -UTF8 (nous ne normalisons pas), -CaseInsensitive (ajoutez 4 bigrammes avec une casse différente), -CaseInsensitiveUTF8 (il y a une condition que les majuscules et les minuscules doivent avoir le même nombre d'octets). Voir l'implémentation ici .

Après cela, nous nous sommes demandé si nous pouvions faire quelque chose de similaire avec de nombreuses expressions régulières. Et ils ont trouvé une solution qui était déjà gâtée dans les benchmarks.

Recherche par de nombreuses expressions régulières

Hyperscan est une bibliothèque d'Intel qui recherche immédiatement de nombreuses expressions régulières. Il utilise l'heuristique pour isoler les sous-mots des expressions régulières sur lesquelles nous avons écrit et beaucoup de SIMD pour rechercher l'automate Glushkov (l'algorithme semble s'appeler Teddy).

En général, tout est dans les meilleures traditions pour tirer le maximum de la recherche d'expressions régulières. La bibliothèque fait vraiment ce qui est déclaré dans ses fonctions.

Heureusement, au cours de mon mois de développement chez ClickHouse, j'ai pu dépasser le développement de 12 ans sur une classe de requêtes décente et j'en suis très satisfait.

Dans Yandex, la bibliothèque Hyperscan est également utilisée dans l'antispam. À en juger par les critiques, elle traite calmement des milliers d'expressions régulières et les recherche rapidement.

La bibliothèque présente plusieurs inconvénients. Le premier est la quantité de mémoire non documentée consommée et une caractéristique étrange que la botte de foin doit être inférieure à 2 ³² octets. Le deuxième - vous ne pouvez pas renvoyer les premières positions gratuitement, les indices d'aiguille les plus à gauche, etc. Et le troisième moins - il y a quelques bugs à l'improviste. Par conséquent, chez ClickHouse, nous avons implémenté les fonctions suivantes à l'aide d'Hyperscan:

- multiMatchAny(h, [n_1, ..., n_k]) - 1, si au moins une des aiguilles est venue avec une botte de foin.
- multiMatchAnyIndex(h, [n_1, ..., n_k]) - tout index d'aiguille qui multiMatchAnyIndex(h, [n_1, ..., n_k]) botte de foin.

Nous sommes intéressés, mais comment rechercher pas exactement, mais approximativement? Et est venu avec plusieurs solutions.

Recherche approximative

La norme dans la recherche approximative est la distance Levenshtein - le nombre minimum de caractères qui peuvent être remplacés, ajoutés et supprimés pour obtenir une chaîne b de longueur n à partir d'une chaîne a de longueur m. Malheureusement, l'algorithme de programmation dynamique naïf fonctionne pour O (mn) ; les meilleurs esprits de ShAD peuvent le faire en O (mn / log max (n, m)) ; il est facile de penser à O ((n + m) ⋅ alpha) , où alpha est la réponse; la science peut le faire pour O ((alpha - | n - m |) min (m, n, alpha) + m + n) (l'algorithme est simple, lu au moins dans le ShAD) ou, si un peu plus clair, pour O (alpha ^ 2 + m + n) . Il y a encore un inconvénient: il est très probablement impossible de se débarrasser du temps quadratique dans le pire des cas polynomialement - Peter Indik a écrit un article très puissant à ce sujet.

Il y a un exercice: imaginez que pour remplacer un personnage dans la distance Levenshtein, vous payez une amende non pas deux, mais deux; puis trouver un algorithme pour O ((n + m) log (n + m)) .

Cela ne fonctionne toujours pas, trop long et trop cher. Mais à l'aide d'une telle distance, nous avons fait la détection de fautes de frappe dans les requêtes.

En plus de la distance de Levenshtein, il y a une distance de Hamming. Avec lui aussi, tout va plutôt mal, mais un peu mieux qu'avec la distance de Levenshtein. Il ne prend pas en compte la suppression des caractères, mais ne considère que pour deux lignes de même longueur le nombre de caractères dans lesquels elles diffèrent. Par conséquent, si nous utilisons la distance pour les chaînes de longueur m <n, alors seulement dans la recherche des sous-chaînes les plus proches.

Comment calculer un tel tableau de divergences (un tableau d de n - m + 1 éléments, où d [i] est le nombre de caractères différents dans le i-ème depuis le début de la superposition) pour O (| Sigma | (n + m) log (n + m) ) ? Tout d'abord, faites | Sigma | masques de bits indiquant si ce symbole est égal à celui considéré. Ensuite, nous calculons la réponse pour chacun des masques Sigma et ajoutons - nous obtenons la réponse d'origine.

Prenons un exemple. abba , sous-chaîne ba , alphabet binaire. Nous obtenons 2 masques 1001, 01 et 0110, 10 .

    a 1001 01 - 0  01 - 0  01 - 1  

    b 0110 10 - 0  10 - 1  10 - 1  

Nous obtenons le tableau [0, 1, 2] - c'est presque la bonne réponse. Mais notez que pour chaque lettre, le nombre de correspondances n'est que le produit scalaire d'une aiguille binaire fixe et de toutes les sous-chaînes de meules de foin. Et pour cela, bien sûr, il y a une transformée de Fourier rapide!

Pour ceux qui ne connaissent pas: la FFT peut multiplier deux polynômes de degrés m <n en un temps O (n log n) , à condition que le travail avec les coefficients soit effectué par unité de temps. Les convolutions sont très similaires aux produits scalaires. Il suffit de dupliquer les coefficients du premier polynôme, de développer et de compléter le second avec le nombre de zéros requis, puis nous obtenons tous les produits scalaires d'une chaîne binaire et toutes les sous-chaînes de l'autre en O (n log n) - une sorte de magie! Mais croyez-moi, c'est absolument réel, et parfois les gens le font.

Mais pas dans ClickHouse. Pour nous, travailler avec | Sigma | = 30 est déjà grand, et la FFT n'est pas l'algorithme pratique le plus agréable pour le processeur ou, comme on dit chez les gens du commun, "la constante est grande".

Par conséquent, nous avons décidé d'examiner d'autres mesures. Nous sommes arrivés à la bioinformatique, où les gens utilisent la distance de n grammes. En fait, nous prenons tous les n-grammes de botte de foin et d'aiguille, considérons 2 multisets avec ces n-grammes. Ensuite, nous prenons la différence symétrique et divisons par la somme des cardinalités de deux multisets avec n-grammes. Nous obtenons un nombre de 0 à 1 - plus proche de 0, plus les lignes sont similaires. Prenons un exemple où n = 4 :

 abcda → {abcd, bcda}; Size = 2 bcdab → {bcda, cdab}; Size = 2         . |{abcd, cdab}| / (2 + 2) = 0.5 

En conséquence, nous avons fait une distance de 4 grammes et y avons collé un tas d'idées de SSE, et nous avons également légèrement affaibli la mise en œuvre en hachages crc32 à deux octets.

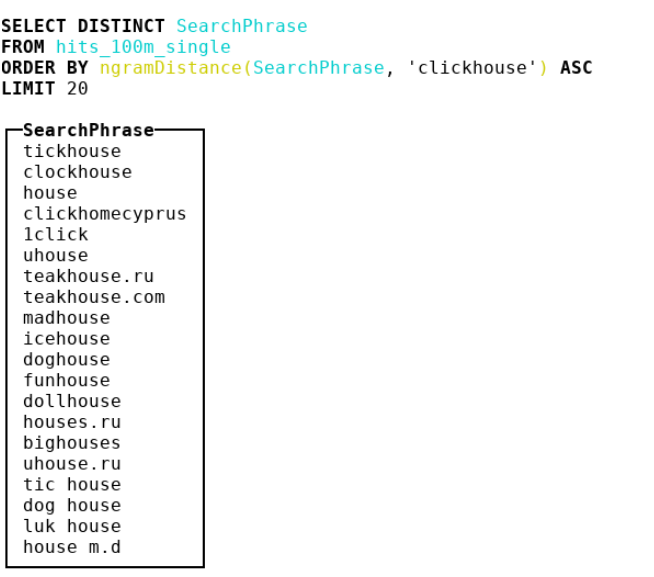
Découvrez l' implémentation . Attention: code très convaincant et optimisé pour les compilateurs.

Je vous conseille particulièrement de faire attention au hack sale pour la casse des minuscules pour les points de code ASCII et russe.

- ngramDistance(haystack, needle) - renvoie un nombre de 0 à 1; plus près de 0, plus les lignes se ressemblent.
- -UTF8, -CaseInsensitive, -CaseInsensitiveUTF8 (hack sale pour les Russes et ASCII).

Hyperscan ne s'arrête pas non plus - il a des fonctionnalités de recherche approximative: vous pouvez rechercher des lignes qui ressemblent à des expressions régulières par la distance constante de Levenshtein. Un automate distance + 1 est créé, qui est interconnecté en supprimant, en remplaçant ou en insérant un caractère, ce qui signifie «bien», après quoi l'algorithme habituel pour vérifier si un automate accepte une ligne particulière est appliqué. Dans ClickHouse, nous les avons implémentés sous les noms suivants:

- multiFuzzyMatchAny(haystack, distance, [n_1, ..., n_k]) - similaire à multiMatchAny, uniquement avec la distance.
- multiFuzzyMatchAnyIndex(haystack, distance, [n_1, ..., n_k]) - similaire à multiMatchAnyIndex, uniquement avec la distance.

Avec l'augmentation de la distance, la vitesse commence à se dégrader considérablement, mais reste toujours à un niveau assez décent.

Terminez la recherche et passez au traitement des chaînes UTF-8. Il y avait aussi beaucoup de choses intéressantes.

Traitement de ligne UTF-8

J'admets qu'il était difficile de franchir le plafond des implémentations naïves dans les chaînes codées UTF-8. Il était particulièrement difficile de visser SIMD. Je partagerai quelques idées sur la façon de procéder.

Rappelez-vous à quoi ressemble une séquence UTF-8 valide:

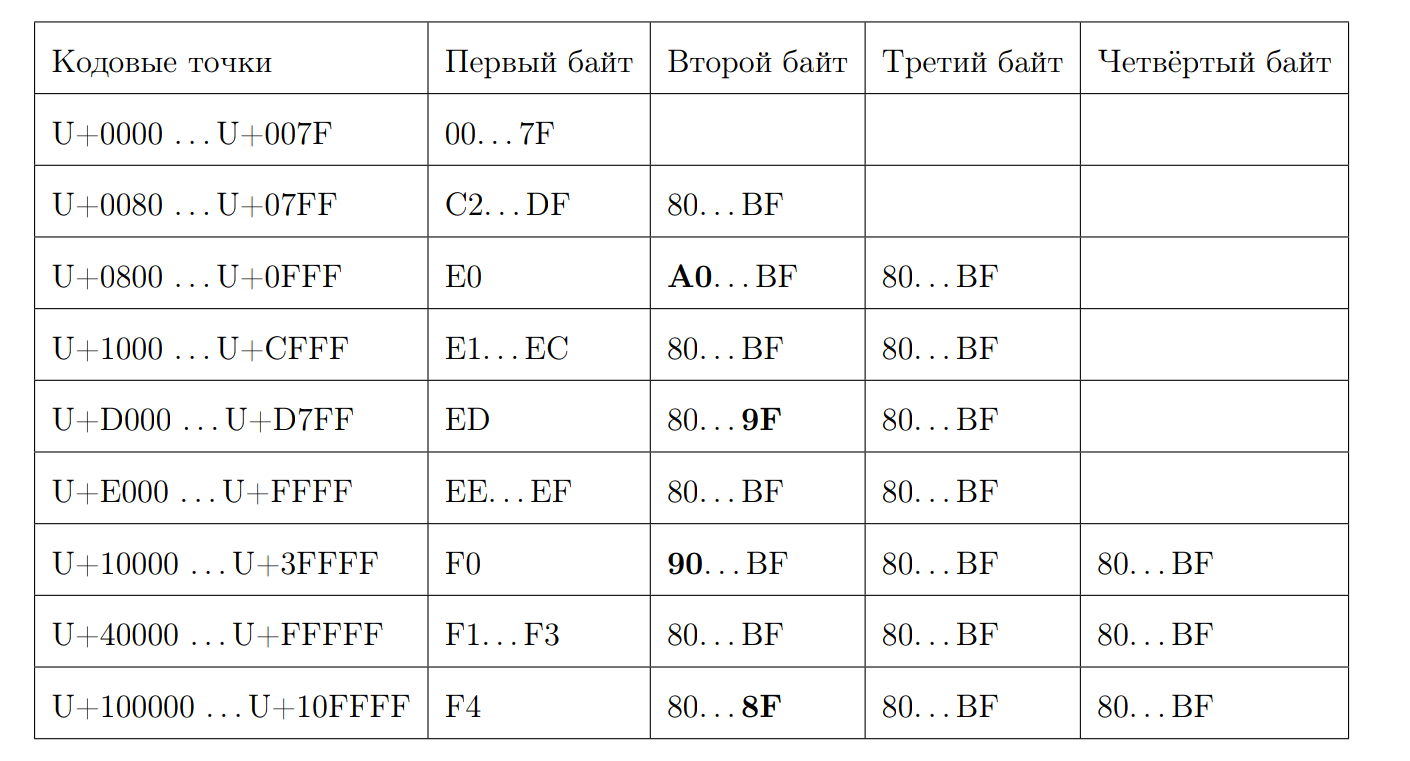
Essayons de calculer la longueur du point de code par le premier octet. C'est là que commence la magie un peu. Encore une fois, nous écrivons quelques propriétés:

- À partir de 0xC et de 0xD, 2 octets
- 0xC2 = 11 0 00010
- 0xDF = 11 0 11111
- 0xE0 = 111 0 0000
- 0xF4 = 1111 0100, il n'y a rien de plus que 0xF4, mais s'il y avait 0xF8, il y aurait une histoire différente
- Répondez 7 moins la position du premier zéro depuis la fin, s'il ne s'agit pas d'un caractère ASCII

Nous calculons la longueur:

 inline size_t seqLength(const UInt8 first_octet) { if (first_octet < 0x80u) return 1; const auto first_zero = bitScanReverse(static_cast<UInt8>(~first_octet)); return 7 - first_zero; } 

Heureusement, nous avons en stock des instructions qui peuvent calculer le nombre de bits zéro, en commençant par les plus significatifs.

 f = __builtin_clz(val) // (bsrl,     ) f(2) = 30, f(8) = 28, f(7) = 29 

Calculer bitScanReverse:

 unsigned int bitScanReverse(unsigned int x) { return 31 - __builtin_clz(x); } 

Essayons de calculer la longueur d'une chaîne UTF-8 par points de code via SIMD. Pour ce faire, examinez chaque octet comme un numéro signé et notez les propriétés suivantes:

- 0xBF = -65
- 0x80 = -128
- 0xC2 = -62
- 0x7F = 127
- tous les premiers octets sont dans [0xC2, 0x7F]
- tous les non-premiers octets sont dans [0x80, 0xBF]

L'algorithme est assez simple. Comparez chaque octet avec -65 et, s'il est supérieur à ce nombre, ajoutez-en un. Si nous voulons utiliser SIMD, c'est la charge habituelle de 16 octets du flux d'entrée. Ensuite, il y a une comparaison d'octets, qui en cas de résultat positif donnera l'octet 0xFF, et dans le cas d'un négatif - 0x00. Puis l'instruction pmovmskb , qui collectera les bits hauts de chaque octet du registre. Ensuite, le nombre de soulignements augmente, nous utilisons l'intrinsèque pour l'instruction popcnt SSE4. Le schéma de cet algorithme peut être illustré par un exemple:

Il s'avère qu'avec la décompression, le traitement par cœur sera d'environ 1,5 Go / s.

Les fonctions sont appelées:

- lengthUTF8(string) - renvoie la longueur d'une chaîne UTF-8 correctement encodée, quelque chose est considéré comme invalide, aucune exception n'est levée.

Nous sommes allés plus loin car nous voulions encore plus de fonctions avec le traitement de chaîne UTF-8. Par exemple, vérifier la validité et transtyper en une expression UTF-8 valide.

Pour vérifier la validité, j'ai pris https://github.com/cyb70289/utf8/ , adapté pour ClickHouse (en fait juste changé le traitement des queues) et j'ai obtenu une vitesse de 1,22 Go / s contre 900 Mo / s pour l'algorithme naïf . Je ne décrirai pas l'algorithme lui-même, il est assez compliqué pour la perception.

- isValidUTF8(string) - renvoie 1 si la chaîne est correctement encodée avec UTF-8, sinon 0.
- toValidUTF8(string) - remplace les caractères UTF-8 non valides par le caractère (U + FFFD). Tous les caractères invalides consécutifs se réduisent en un seul caractère de remplacement. Pas de science fusée.

En général, dans les lignes UTF-8, en raison du schéma statique moins agréable, il est toujours difficile de trouver quelque chose de bien optimisé.

Et ensuite?

Permettez-moi de vous rappeler que c'était ma thèse. Bien sûr, je l'ai défendue 10/10. Nous l'avons déjà accompagnée à Highload ++ Siberia (bien qu'il me semble qu'elle n'intéressait guère personne). Regardez la présentation . J'ai aimé que la partie pratique de la thèse ait donné lieu à de nombreuses recherches intéressantes. Et voici le diplôme lui-même. Il contient beaucoup de fautes de frappe, car personne ne l'a lu. :)

Dans le cadre de la préparation du diplôme, j'ai effectué un tas d'autres travaux similaires (les liens conduisent à des demandes de pool):

- Fonction de concaturation optimisée 2 fois ;
- Création du format python le plus simple pour les requêtes ;
- LZ4 accéléré de 4% ;
- J'ai fait un excellent travail sur SIMD pour ARM et PPC64LE ;
- Et il a conseillé quelques étudiants du FCS diplômés de ClickHouse.

En fin de compte, il s'est avéré que, selon mon expérience, chaque mois, Lesha a essayé de me chanter ClickHouse est le système le plus agréable pour écrire du code haute performance, où il y a de la documentation, des commentaires, un excellent support développeur et devops. ClickHouse est vraiment génial. Fatigué de changer les formats JSON? Venez à Lesha et demandez une tâche de n'importe quel niveau - il la fournira pour vous, et au cours du week-end, vous aurez un grand plaisir à écrire du code.

Mais avec toutes les réalisations de ClickHouse et sa conception, il ne s'agit probablement pas d'eux. Pas principalement en eux.

J'ai suivi 4 ans d'études de premier cycle à la FCS, en juin j'ai obtenu un diplôme du HSE avec mention, travaillé pendant un an et demi dans une équipe géniale à Yandex, après avoir bien pompé. Sans expérience totale tout ce temps et le fer Rien d'écrit dans le post n'aurait fonctionné. FCN est très cool, si vous en tirez le maximum. Merci à Vana Puzyrevsky ivan_puzyrevskiy , Ignat Kolesnichenko, Gleb Evstropov, Max Babenko maxim_babenko pour leur rencontre dans ma drôle d'aventure sur FCN. Et aussi merci à tous les professeurs qui m'ont appris quelque chose.