"Si vous lisez l'inscription" buffle "sur la cage de l'éléphant, n'en croyez pas vos yeux" Kozma Prutkov

Dans un article précédent sur la conception orientée modèle , il a été démontré pourquoi un modèle objet est nécessaire, et il a été prouvé que sans ce modèle objet, on ne peut parler de conception basée sur un modèle que comme un blizzard marketing, dénué de sens et impitoyable. Mais lorsqu'un modèle d'objet apparaît, les ingénieurs compétents ont toujours une question raisonnable: quelle preuve y a-t-il que le modèle mathématique d'un objet correspond à un objet réel?

Un exemple de réponse à cette question est donné dans un article sur la conception orientée modèle d'un entraînement électrique. Dans cet article, nous considérerons un exemple de création d'un modèle pour les systèmes de climatisation de l'aviation, diluant la pratique avec quelques considérations générales théoriques.

Création d'un modèle fiable de l'objet. Théorie

Afin de ne pas tirer sur le caoutchouc, je vais vous parler immédiatement de l'algorithme de création d'un modèle pour une conception orientée modèle. Il ne comporte que trois étapes simples:

Étape 1. Développer un système d'équations algébriques-différentielles qui décrivent le comportement dynamique des systèmes simulés. C'est simple si vous connaissez la physique du processus. De nombreux scientifiques ont déjà développé pour nous les lois physiques de base du nom de Newton, Brenuli, Navier Stokes et d'autres Shtangels of Compasses et Rabinovich.

Étape 2. Dans le système résultant, isolez l'ensemble des coefficients empiriques et des caractéristiques de l'objet de simulation qui peuvent être obtenus à partir des tests.

Étape 3. Effectuer des tests de l'objet et ajuster le modèle en fonction des résultats des expériences sur le terrain, afin qu'il corresponde à la réalité, avec le degré de détail nécessaire.

Comme vous pouvez le voir, seulement deux trois.

Exemple pratique

Le système de climatisation (SCR) de l'avion est connecté au système de maintien automatique de la pression. La pression dans l'avion doit toujours être supérieure à la pression externe, tandis que le taux de variation de pression doit être tel que les pilotes et les passagers ne saignent pas du nez et des oreilles. Par conséquent, le système de contrôle de l'entrée et de la sortie d'air est important pour la sécurité, et des systèmes de test coûteux sont mis en place pour son développement. Ils créent des températures et des pressions d'altitude de vol, reproduisent des modes de décollage et d'atterrissage sur des aérodromes de hauteurs différentes. Et la question du développement et du débogage de systèmes de contrôle pour les devises fortes est à son plein potentiel. Combien de temps allons-nous conduire le banc d'essai pour obtenir un système de contrôle satisfaisant? De toute évidence, si nous adaptons le modèle de contrôle au modèle objet, le cycle de travail sur le banc d'essai peut être considérablement réduit.

Le système de climatisation de l'aviation se compose des mêmes échangeurs de chaleur que tout autre système thermique. Batterie - c'est aussi une batterie en Afrique, uniquement la climatisation. Mais en raison de la limitation de la masse au décollage et des dimensions de l'avion, les échangeurs de chaleur sont réalisés aussi compacts que possible et aussi efficaces que possible afin de transférer le plus de chaleur possible de la masse inférieure. En conséquence, la géométrie devient assez bizarre. Comme par exemple dans le cas considéré. La figure 1 montre un échangeur de chaleur à plaques, dans lequel une membrane est utilisée entre les plaques pour améliorer le transfert de chaleur. Le liquide de refroidissement chaud et froid alternent dans les canaux, tandis que le sens d'écoulement est transversal. Un liquide de refroidissement est fourni à la coupe frontale, l'autre sur le côté.

Pour résoudre le problème de contrôle SCR, nous devons savoir combien de chaleur est transférée d'un milieu à un autre dans un tel échangeur de chaleur par unité de temps. Le taux de changement de température en dépend, que nous régulons.

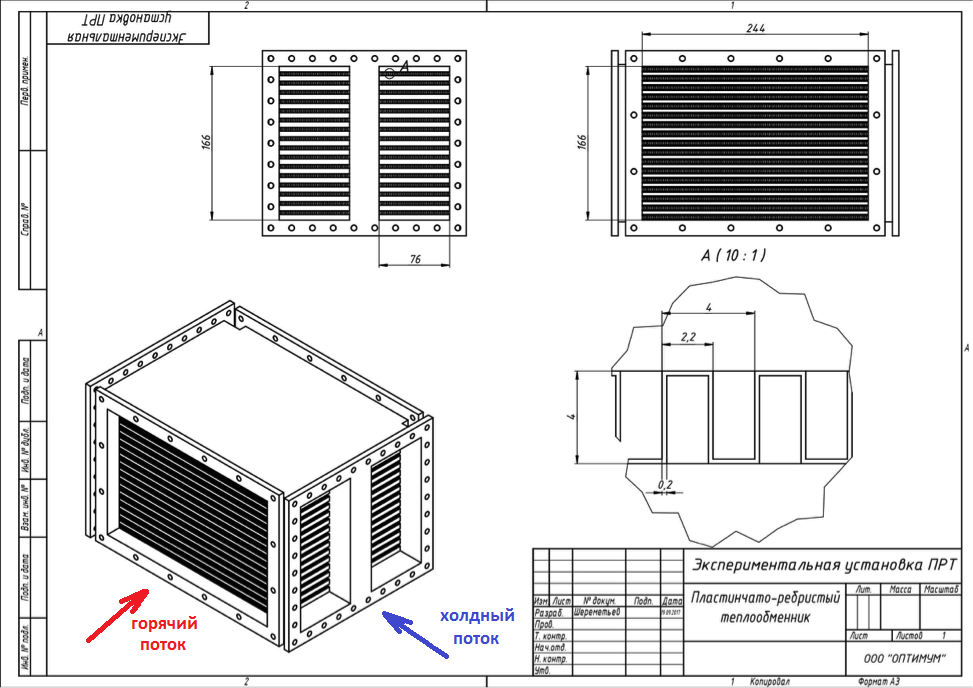
Figure 1. Diagramme de l'échangeur de chaleur de l'avion.

Problèmes de modélisation. Partie hydraulique

À première vue, la tâche est assez simple, il faut calculer le débit massique à travers les canaux de l'échangeur de chaleur et le flux de chaleur entre les canaux.
Le débit massique du liquide de refroidissement dans les canaux est calculé à l'aide de la formule de Bernoulli:

où:
ΔP est la chute de pression entre deux points;
ξ est le coefficient de frottement du liquide de refroidissement;
L est la longueur du canal;
d est le diamètre hydraulique du canal;
ρ est la densité du liquide de refroidissement;
ω est la vitesse du liquide de refroidissement dans le canal.

Pour un canal de forme arbitraire, le diamètre hydraulique est calculé par la formule:

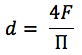
où:
F est l'aire de l'alésage;
P - périmètre de canal mouillé.

Le coefficient de frottement est calculé selon des formules empiriques et dépend de la vitesse d'écoulement et des propriétés du liquide de refroidissement. Pour différentes géométries, différentes dépendances sont obtenues, par exemple, la formule d'écoulement turbulent dans des tuyaux lisses:

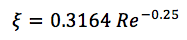
où:
Re est le nombre de Reynolds.

Pour l'écoulement dans des canaux plats, la formule suivante peut être utilisée:

À partir de la formule de Bernoulli, vous pouvez calculer la chute de pression pour une vitesse donnée, ou vice versa, calculer la vitesse du liquide de refroidissement dans le canal, sur la base d'une chute de pression donnée.

Transfert de chaleur

Le flux de chaleur entre le liquide de refroidissement et le mur est calculé par la formule:

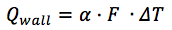
où:
α [W / (m2 × deg)] - coefficient de transfert de chaleur;
F est l'aire de l'alésage.

Pour les problèmes d'écoulement de liquides de refroidissement dans les canalisations, un nombre suffisant d'études a été réalisé et il existe de nombreuses méthodes de calcul, et en règle générale, tout se résume à des dépendances empiriques, pour le coefficient de transfert de chaleur α [W / (m2 × deg)]

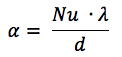
où:
Nu est le nombre de Nusselt,
λ est la conductivité thermique du liquide [W / (m × deg)]
d est le diamètre hydraulique (équivalent).

Les dépendances de critères empiriques sont utilisées pour calculer le nombre de Nusselt (critère), par exemple, la formule de calcul du nombre de Nusselt d'un tuyau rond ressemble à ceci:

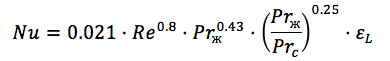
Ici, nous voyons déjà le nombre de Reynolods, le nombre de Prandtl à la température de la paroi et à la température du fluide, et le coefficient d'inégalité. ( Source )

Pour les échangeurs de chaleur à plaques ondulées, la formule est similaire ( Source ):

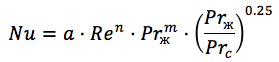
où:
n = 0,73 m = 0,43 pour un écoulement turbulent,
le coefficient a - varie entre 0,065 et 0,6 selon le nombre de plaques et le régime d'écoulement.

Notez que ce coefficient est calculé pour un seul point du flux. Pour le point suivant, nous avons une température de liquide différente (elle s'est réchauffée ou refroidie), une température de paroi différente et, en conséquence, tous les nombres de Reynolds et les nombres de Prandtl flottent.

À ce stade, tout mathématicien dira qu'il est impossible de calculer exactement le système dans lequel le coefficient change 10 fois, et il aura raison.

Tout ingénieur en exercice dira que chaque échangeur de chaleur est différent dans la fabrication et qu'il est impossible de calculer les systèmes, et il aura également raison.

Mais qu'en est-il de la conception orientée modèle? Tout est-il parti?

Les vendeurs avancés de logiciels occidentaux dans cet endroit vous associeront à un supercalculateur et à des systèmes de calcul 3D, tels que «sans lui en aucune façon». Et vous devez exécuter le calcul pendant une journée pour obtenir la distribution de température pendant 1 minute.

Il est clair que ce n'est pas notre option, nous devons déboguer le système de contrôle, sinon en temps réel, du moins dans un avenir prévisible.

Méthode Poke

Un échangeur de chaleur est fabriqué, une série de tests est effectuée et un tableau de l'efficacité de la température en régime permanent est établi aux débits donnés. Simple, rapide et fiable, comme les données obtenues à partir des tests.

L'inconvénient de cette approche est qu'il n'y a pas de caractéristiques dynamiques de l'objet. Oui, nous savons quel sera le flux de chaleur en régime permanent, mais nous ne savons pas combien de temps il sera établi lors du passage d'un mode de fonctionnement à un autre.

Par conséquent, après avoir calculé les caractéristiques nécessaires, nous avons mis en place le système de contrôle directement pendant les tests, ce que nous aimerions éviter dès le début.

Approche orientée modèle

Pour créer un modèle d'échangeur de chaleur dynamique, il est nécessaire d'utiliser des données de test, pour éliminer les incertitudes dans les formules de calcul empiriques - le nombre de Nusselt et la résistance hydraulique.

La décision est simple, comme toute ingénieuse. Nous prenons la formule empirique, menons des expériences et déterminons la valeur du coefficient a, éliminant ainsi l'incertitude de la formule.

Dès que nous avons une certaine valeur du coefficient de transfert de chaleur, tous les autres paramètres sont déterminés par les lois physiques de base de la conservation. La différence de température et le coefficient de transfert de chaleur déterminent la quantité d'énergie transférée au canal par unité de temps.

Connaissant le flux d'énergie, il est possible de résoudre les équations de conservation de la masse d'énergie et de l'impulsion pour le liquide de refroidissement dans le canal hydraulique. Par exemple, ceci:

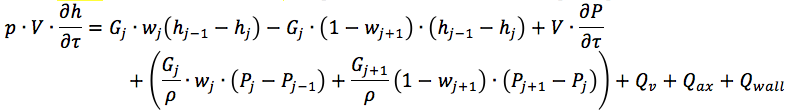
Dans notre cas, le flux de chaleur entre le mur et le liquide de refroidissement - Qwall - reste indéterminé. Plus de détails peuvent être trouvés ici ...

Et aussi l'équation de la dérivée de température pour la paroi du canal:

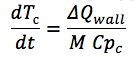
où:
_Mur ΔQ - la différence entre le flux entrant et sortant vers la paroi du canal;
M est la masse de la paroi du canal;
C _pc est la capacité thermique du matériau du mur.

Précision du modèle

Comme mentionné ci-dessus, dans l'échangeur de chaleur, nous avons une distribution de température sur la surface de la plaque. Pour la valeur en régime permanent, on peut prendre la moyenne sur les plaques et l'utiliser, en présentant l'échangeur de chaleur entier comme un point concentré, dans lequel le transfert de chaleur se produit sur toute la surface de l'échangeur de chaleur à la même différence de température. Mais pour les modes transitoires, cette approximation peut ne pas fonctionner. L'autre extrême est de faire plusieurs centaines de milliers de points et de charger le Super Computer, ce qui ne nous convient pas non plus, puisque la tâche est de configurer le système de contrôle en temps réel, ou mieux, plus rapidement.

La question se pose, de combien de sections avez-vous besoin pour casser l'échangeur de chaleur pour obtenir une précision et une vitesse de calcul acceptables?

Comme toujours par hasard, j'avais en main un modèle d'échangeur de chaleur à amine. L'échangeur de chaleur est un tube, le fluide caloporteur circule dans les tuyaux, et chauffé entre les puits. Pour simplifier la tâche, le tube entier de l'échangeur de chaleur peut être représenté comme un tuyau équivalent, et le tuyau lui-même peut être représenté comme un ensemble de cellules de conception discrètes, dans chacune desquelles un modèle ponctuel de transfert de chaleur est calculé. Le schéma du modèle d'une seule cellule est illustré à la figure 2. Le canal d'air chaud et le canal d'air froid sont connectés à travers une paroi qui assure le transfert de chaleur entre les canaux.

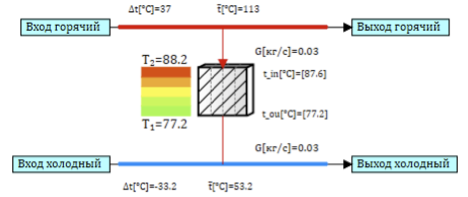
Figure 2. Modèle de cellule d'échangeur de chaleur.

Le modèle d'échangeur de chaleur tubulaire est facilement personnalisable. Vous ne pouvez modifier qu'un seul paramètre - le nombre de sections le long de la longueur du tuyau et consulter les résultats des calculs pour différentes partitions. Nous calculerons plusieurs options, en partant de la division en 5 points de longueur (Fig. 3) et jusqu'à 100 points de longueur (Fig. 4).

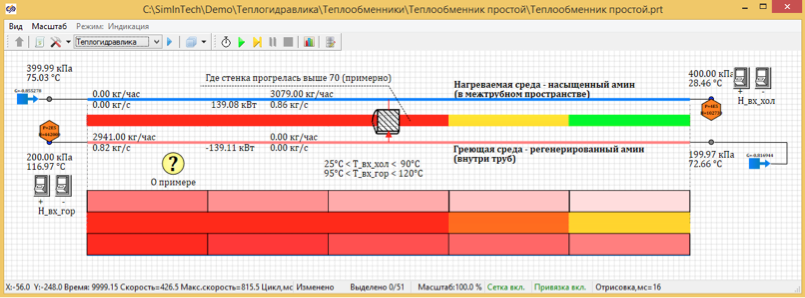
Figure 3. Distribution de température stationnaire de 5 points de conception.

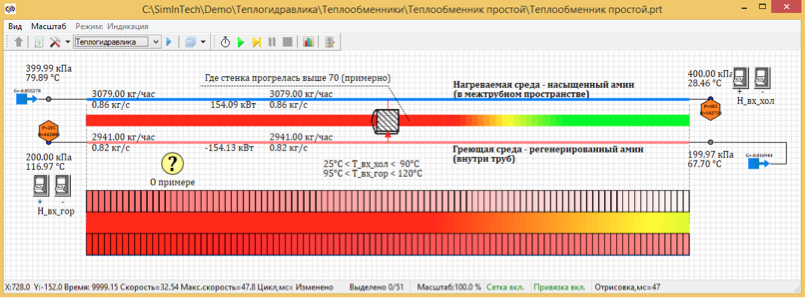
Figure 4. Distribution de température stationnaire de 100 points de conception.

À la suite des calculs, il s'est avéré que la température à l'état stationnaire lorsqu'elle était divisée par 100 points était de 67,7 degrés. Et lorsqu'elle est divisée en 5 points calculés, la température est de 72, 66 degrés C.

De plus, la vitesse de calcul par rapport au temps réel est affichée dans la partie inférieure de la fenêtre.
Voyons comment la température en régime permanent et la vitesse de calcul changent en fonction du nombre de points de conception. La différence de températures en régime permanent dans les calculs avec un nombre différent de cellules de calcul peut être utilisée pour évaluer la précision du résultat.

Tableau 1. La dépendance de la température et de la vitesse de calcul sur le nombre de points de conception sur la longueur de l'échangeur de chaleur.

En analysant ce tableau, nous pouvons tirer les conclusions suivantes:

• La vitesse de calcul diminue proportionnellement au nombre de points de conception dans le modèle d'échangeur de chaleur.
• Le changement dans la précision du calcul se produit de façon exponentielle. À mesure que le nombre de points augmente, le raffinement à chaque augmentation subséquente diminue.

Dans le cas d'un échangeur de chaleur à plaques avec un caloporteur à flux croisé, comme sur la figure 1, la création d'un modèle équivalent à partir de cellules de conception élémentaire est légèrement compliquée. Nous devons connecter les cellules de manière à organiser le flux transversal. Pour 4 cellules, le circuit ressemblera à celui illustré à la figure 5.

Le flux de liquide de refroidissement est divisé en deux canaux le long de la branche chaude et froide, les canaux seront connectés à travers des structures thermiques, de sorte qu'en traversant le canal, le liquide de refroidissement échange de la chaleur avec différents canaux. Simulant le flux transversal, le caloporteur chaud circule de gauche à droite (voir Fig.5) dans chaque canal, échangeant séquentiellement de la chaleur avec les canaux du caloporteur froid, qui va de bas en haut (voir Fig.5). Le point le plus chaud se trouve dans le coin supérieur gauche, car le caloporteur chaud échange de la chaleur avec le liquide de refroidissement déjà chauffé du canal froid. Et le plus froid en bas à droite, où le liquide de refroidissement froid échange de la chaleur avec le liquide de refroidissement chaud qui a déjà refroidi dans la première section.

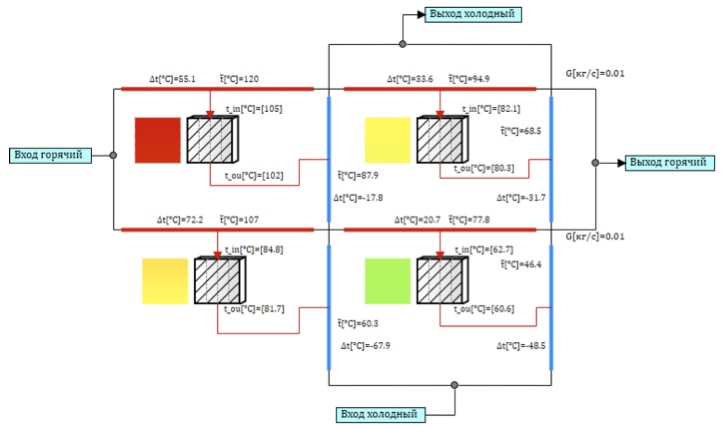
Figure 5. Un modèle d'écoulement transversal de 4 cellules de conception.

Un tel modèle d'échangeur de chaleur à plaques ne prend pas en compte le transfert de chaleur entre les cellules du fait de la conductivité thermique et ne prend pas en compte le mélange du fluide caloporteur, chaque canal étant isolé.

Mais dans notre cas, cette dernière limitation ne réduit pas la précision, car dans la conception de l'échangeur de chaleur, la membrane ondulée divise le flux en de nombreux canaux isolés le long du liquide de refroidissement (voir Fig.1). Voyons ce qui se passe avec la précision du calcul lors de la modélisation d'un échangeur de chaleur à plaques avec une augmentation du nombre de cellules de conception.

Pour l'analyse de précision, nous utilisons deux options pour diviser l'échangeur de chaleur dans la cellule de conception:

1. Chaque cellule carrée contient deux éléments hydrauliques (flux froid et chaud) et un élément thermique. (voir figure 5)
2. Chaque cellule carrée contient six éléments hydrauliques (trois sections en flux chaud et froid) et trois éléments thermiques.

Dans ce dernier cas, nous utilisons deux types de connexion:

• contre-courant des courants froids et chauds;
• flux associé de flux froid et chaud.

Le courant venant en sens inverse augmente l'efficacité par rapport au courant transversal et le courant associé diminue. Avec un grand nombre de cellules, la moyenne du flux se produit et tout devient proche du flux transversal réel qui l'entoure (voir figure 6).

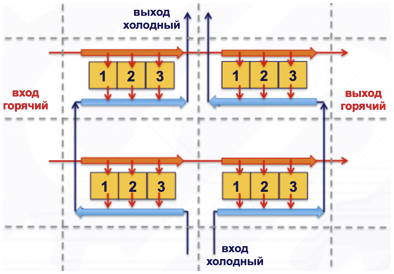
Figure 6. Un modèle d'écoulement transversal de quatre cellules avec 3 éléments.

La figure 7 montre les résultats d'une distribution de température stationnaire à l'état stationnaire dans l'échangeur de chaleur lors de la fourniture d'air à une température de 150 ° C le long de la ligne chaude et 21 ° C le long de la ligne froide, pour diverses options de partitionnement du modèle. La couleur et les nombres sur la cellule reflètent la température moyenne des parois de la cellule.

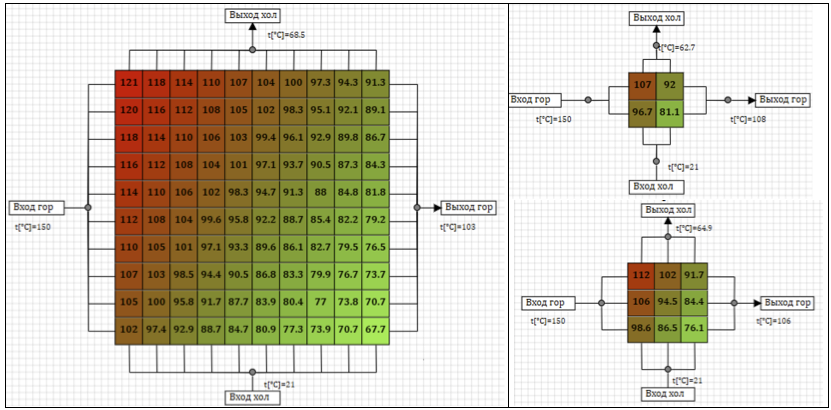
Figure 7. Températures à l'état stable pour différents schémas de calcul.

Le tableau 2 montre la température à l'état stationnaire de l'air chauffé après l'échangeur de chaleur, en fonction de la partition du modèle d'échangeur de chaleur en cellules.

Tableau 2. Dépendance de la température sur le nombre de cellules de conception dans l'échangeur de chaleur.

Avec une augmentation du nombre de cellules de calcul dans le modèle, la température finale en régime permanent augmente. La différence entre la température de régime permanent à différentes partitions peut être considérée comme un indicateur de la précision du calcul. On voit qu'avec une augmentation du nombre de cellules de calcul, la température tend vers la limite, et l'augmentation de la précision n'est pas proportionnelle au nombre de points de calcul.

La question se pose, mais de quelle précision du modèle avons-nous besoin?

La réponse à cette question dépend de l'objectif de notre modèle. Étant donné que cet article concerne la conception orientée modèle, nous créons un modèle pour le réglage du système de contrôle. Cela signifie que la précision du modèle doit être comparable à la précision des capteurs utilisés dans le système.

Dans notre cas, la température est mesurée par un thermocouple dont la précision est de ± 2,5 ° C. Toute précision supérieure dans le but de régler le système de contrôle est inutile, notre véritable système de contrôle "ne le verra tout simplement pas". Ainsi, si nous supposons que la température limite avec un nombre infini de partitions est de 70 ° C, alors un modèle qui nous donne plus de 67,5 ° C sera d'une précision suffisante. Tous les modèles avec 3 points dans la cellule de calcul et les modèles sont plus grands que 5x5 avec un point dans la cellule. (Surligné en vert dans le tableau 2)

Modes de fonctionnement dynamiques

Pour évaluer le mode dynamique, nous évaluons le processus de changement de température aux points les plus chauds et les plus froids de la paroi de l'échangeur de chaleur pour divers schémas de conception. (voir fig.8)


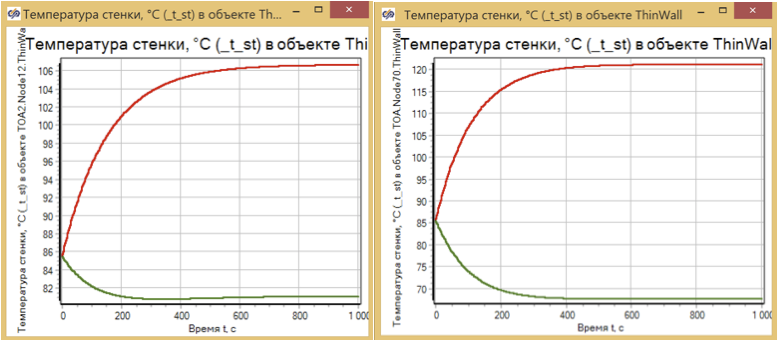
Figure 8. Échangeur de chaleur se réchauffant. Modèles de dimension 2x2 et 10x10.

On peut voir que le temps du processus de transition et sa nature même, ne dépendent pratiquement pas du nombre de cellules calculées et sont déterminés uniquement par la masse du métal chauffé.

Ainsi, nous concluons que pour une simulation honnête de l'échangeur de chaleur dans les modes de 20 à 150 ° C, avec la précision requise par le système de contrôle SCR, environ 10 à 20 points calculés suffisent.

Expérimentez la configuration du modèle dynamique

, , , , , .

, , . 9 . , , , .

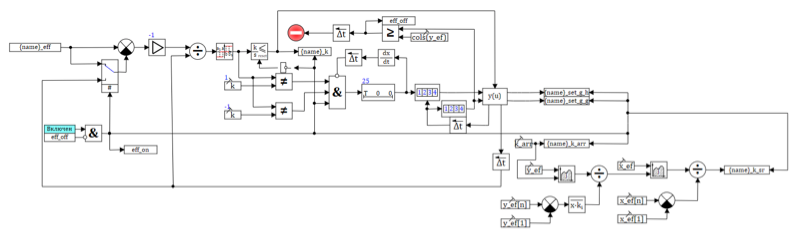
9. .

a . , ( ) . , 0.492 0.655

0.6, , , .

– :

:
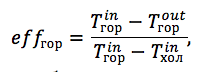
eff – ;
T ⁱⁿ – ;
T ^out – ;
T ⁱⁿ – .

3 .

3. %

. , , , , .

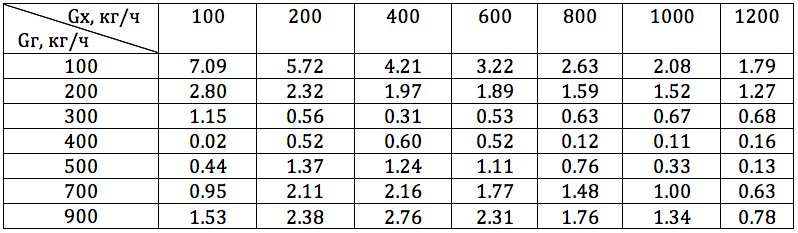
, 10 .

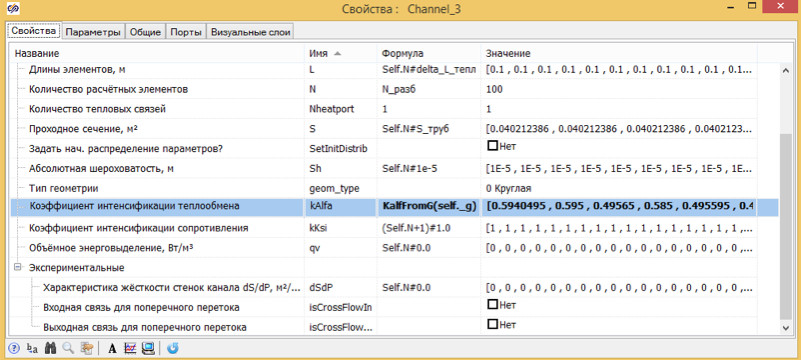
10. .

Conclusions

• - .
  
• .
  
• .
  
• - !

. .