Série «Le bruit blanc dessine un carré noir»
L'histoire du cycle de ces publications commence avec le fait que dans
le livre
de G. Sekey «Paradoxes in Probability Theory and Mathematical Statistics» (
p. 43 ), l'énoncé suivant a été découvert:

Fig. 1.
Selon l'analyse, le commentaire des premières publications (
partie 1 ,
partie 2 ) et le raisonnement qui a suivi ont mûri l'idée de présenter ce théorème sous une forme plus visuelle.
La plupart des membres de la communauté connaissent le triangle de Pascal, en raison de la distribution de probabilité binomiale et de nombreuses lois connexes. Pour comprendre le mécanisme de la formation du triangle de Pascal, nous allons l'étendre plus en détail, avec le déploiement des flux de sa formation. Dans le triangle Pascal, les nœuds sont formés par le rapport de 0 et 1, la figure ci-dessous.
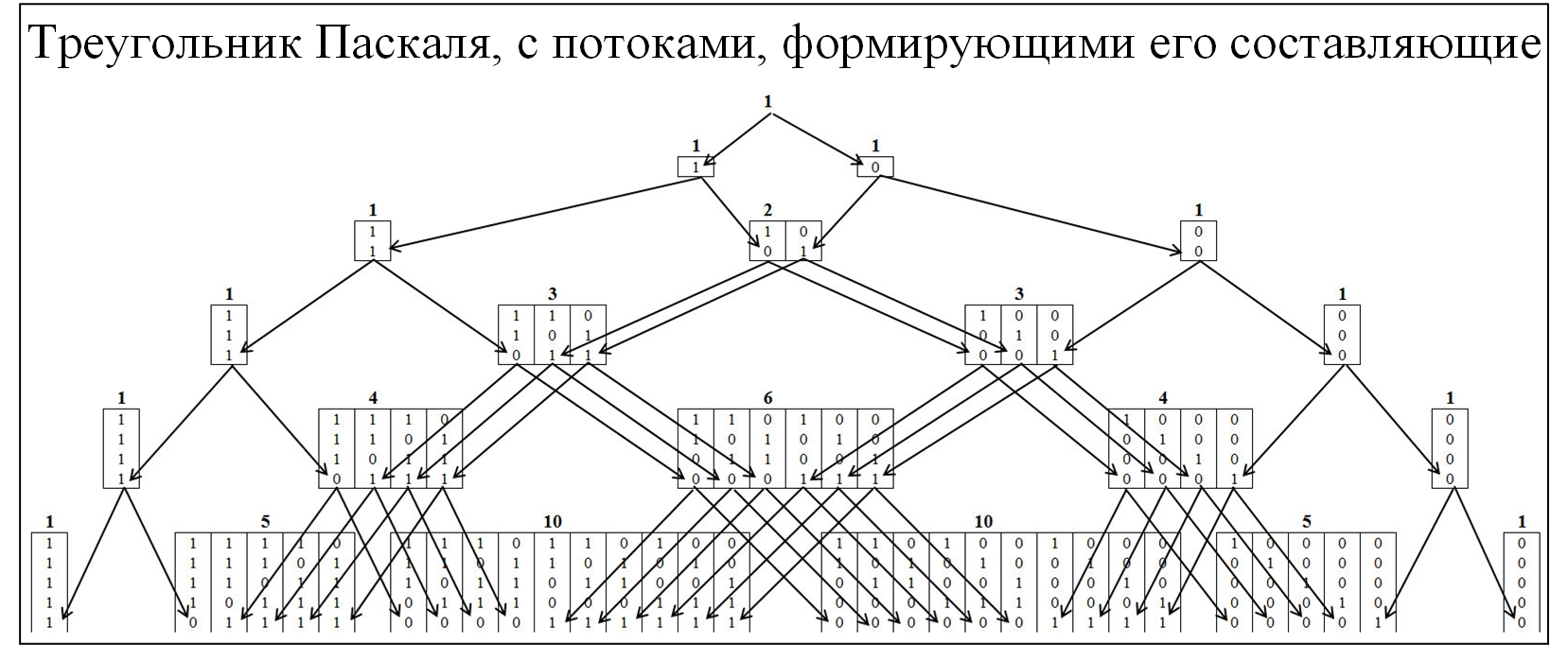
Fig. 2.
Pour comprendre le théorème Erds-Renyi, nous allons composer un modèle similaire, mais les nœuds seront formés à partir des valeurs dans lesquelles les plus grandes chaînes sont présentes, constituées séquentiellement des mêmes valeurs. Le clustering sera effectué selon la règle suivante: chaînes 01/10, au cluster «1»; chaîne 00/11, pour regrouper «2»; chaînes 000/111, au cluster "3", etc. Dans ce cas, nous allons diviser la pyramide en deux composantes symétriques Figure 3.

Fig. 3.
La première chose qui attire votre attention est que tous les mouvements se produisent d'un cluster inférieur à un cluster supérieur et vice versa ne peuvent pas l'être. C'est naturel, car si une chaîne de taille j s'est formée, elle ne peut plus disparaître.
En déterminant l'algorithme de concentration des nombres, nous avons réussi à obtenir la formule de récurrence suivante, dont le mécanisme est illustré dans les figures 4-6.
Indique les éléments dans lesquels les nombres sont concentrés, où n est le nombre de caractères du nombre (nombre de bits) et la longueur de la chaîne maximale est m. Et chaque élément recevra un indice n; mJ.
Notons que le nombre d'éléments est passé de n; mJ à n + 1; m + 1J, n; mjn + 1; m + 1.

Fig. 4.
La figure 4 montre que pour le premier cluster, il n'est pas difficile de déterminer les valeurs de chaque ligne. Et cette dépendance est égale à:

Fig. 5.
Nous déterminons pour le deuxième groupe, avec la longueur de chaîne m = 2, figure 6.
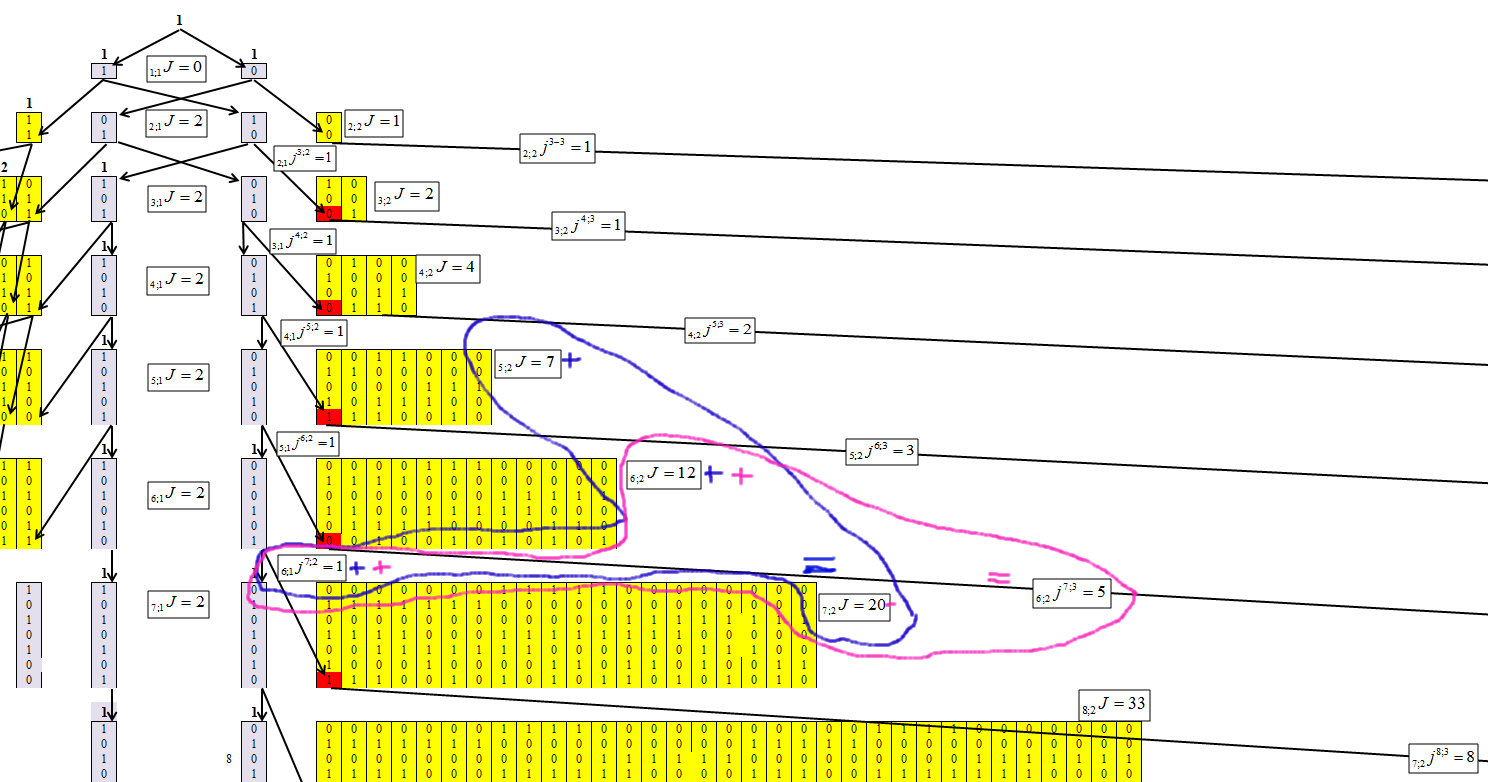
Fig. 6.
La figure 6 montre que pour le deuxième cluster, la dépendance est égale à:

Fig. 7.
Nous déterminons pour le troisième groupe, avec la longueur de chaîne m = 3, figure 8.
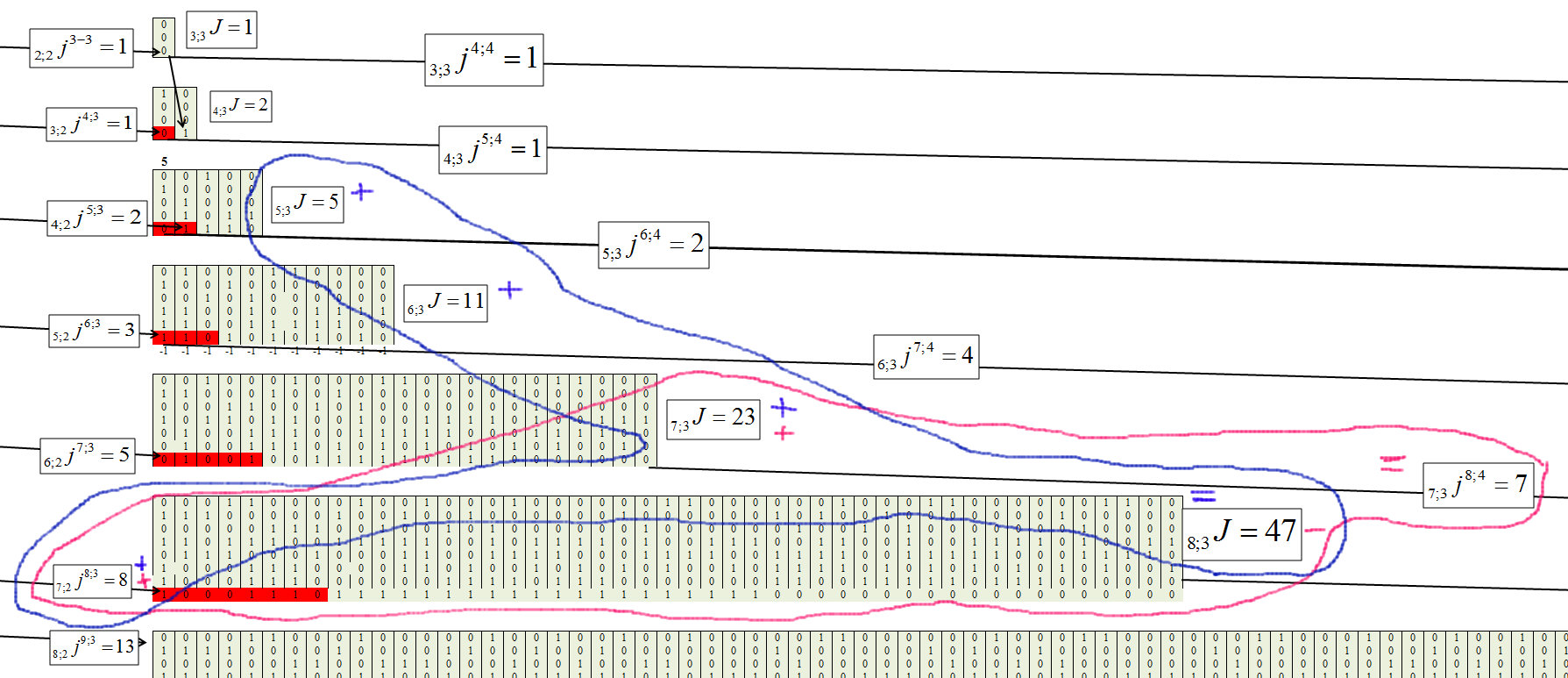
Fig. 8.

Fig. 9.
La formule générale de chaque élément prend la forme:

Fig. 10.

Fig. 11.
Vérification
Pour la vérification, nous utilisons la propriété de cette séquence, qui est représentée sur la figure 12. Elle consiste dans le fait que les derniers membres d'une ligne d'une certaine position prennent une valeur unique pour toutes les lignes avec une longueur de ligne croissante.
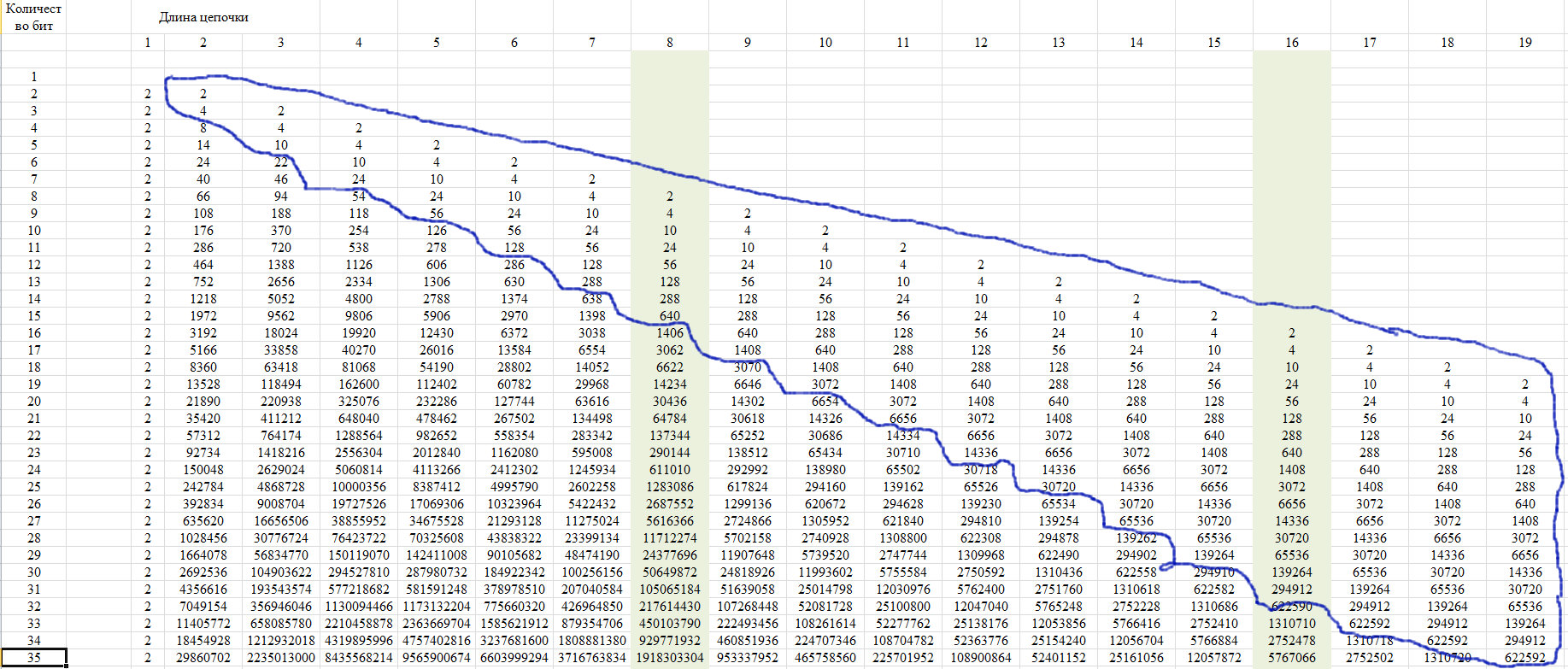
Fig. 12.
Cette propriété est due au fait qu'avec une longueur de chaîne supérieure à la moitié de la ligne entière, une seule chaîne de ce type est possible. Nous le montrons dans le diagramme de la figure 13.

Fig. 13.
En conséquence, pour des valeurs de k <n-2, on obtient la formule:
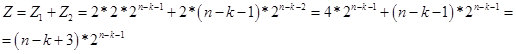
Fig. 14.
En fait, la valeur de Z est le nombre potentiel de nombres (options dans une chaîne de n bits) qui contiennent une chaîne de k éléments identiques. Et selon la formule de récurrence, on détermine le nombre de nombres (options dans une chaîne de n bits) dans lesquels la chaîne de k éléments identiques est la plus grande. Pour l'instant, je suppose que la valeur Z est virtuelle. Par conséquent, dans la région n / 2, il passe dans l'espace réel. Dans la figure 15, un écran avec des calculs.

Fig. 15.
Montrons un exemple d'un mot de 256 bits, qui peut être déterminé par cet algorithme.

Fig. 16.
Si elle est déterminée par les normes de fiabilité de 99,9% pour le GSPCH, alors la clé de 256 bits doit contenir des chaînes consécutives de caractères identiques avec le nombre de 5 à 17. Autrement dit, selon les normes pour le GSPCH, afin qu'elle réponde à l'exigence de similitude d'aléatoire avec une fiabilité de 99,9%, GSPCH, en 2000 les tests (délivrant un résultat sous la forme d'un nombre binaire 256 bits) ne devraient donner qu'un résultat dans lequel la longueur de série maximale des mêmes valeurs: soit moins de 4, soit plus de 17.
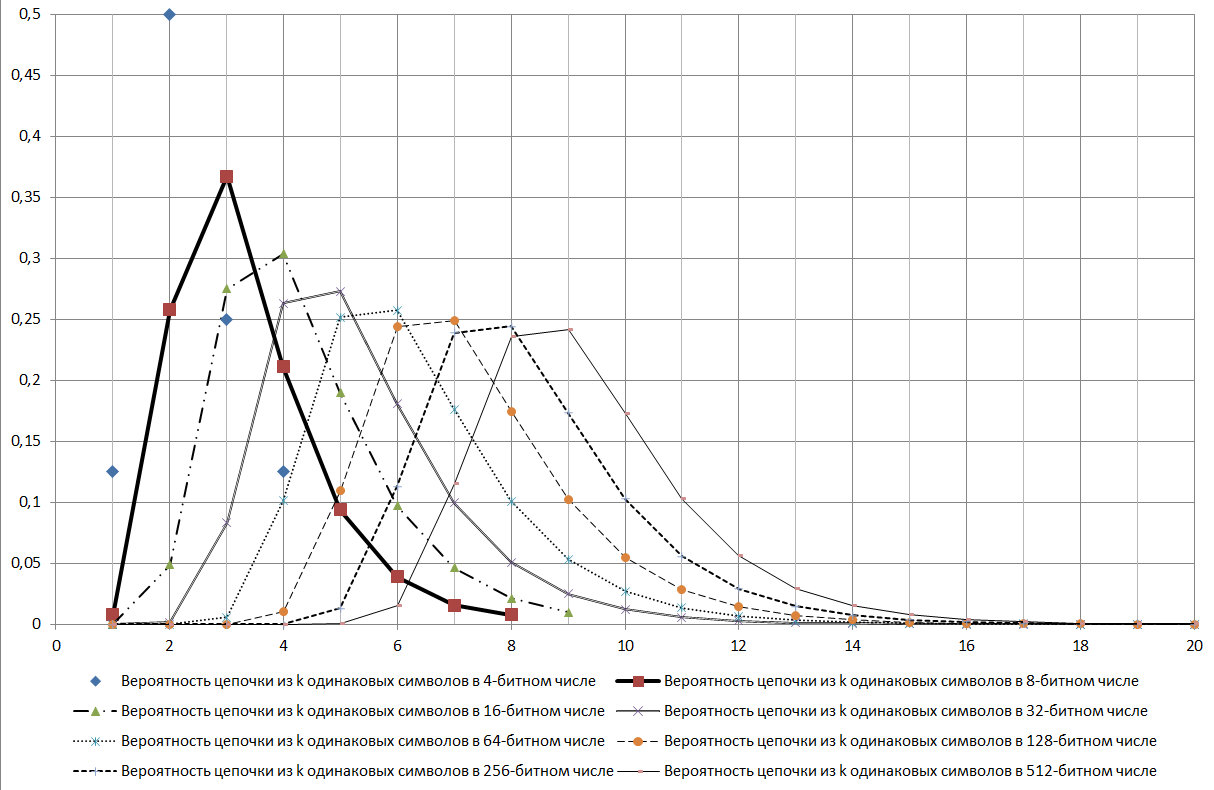
Fig. 17.
Comme le montre le diagramme de la figure 17, la chaîne log2N est un mode de distribution considéré.
Au cours de l'étude, de nombreux signes de diverses propriétés de cette séquence ont été trouvés. En voici quelques uns:
- il doit être bien testé par le critère du chi carré;
- donne des signes de l'existence de propriétés fractales;
- peut être un bon critère pour identifier divers processus aléatoires.
Et bien d'autres connexions.
Vérifié si une telle séquence existe également sur la L e
Encyclopédie en ligne des séquences entières (OEIS) (Online Encyclopedia of Integer Sequences) dans le numéro de séquence
A006980 , référence est faite à la publication
JL Yucas, Counting special sets of binary Lyndon words, Ars Combin. , 31 (1991), p. 21-29 , où la séquence est indiquée à la page 28 (dans le tableau). Dans la publication, les lignes sont numérotées 1 de moins, mais les valeurs sont les mêmes. En général, la publication porte sur les
paroles de Lyndon , c'est-à-dire qu'il est fort possible que le chercheur ne soupçonne même pas que cette série était liée à cet aspect.
Revenons au théorème d'Erdhs-Renyi. D'après les résultats de cette publication, on peut dire que dans la formulation qui est présentée, ce théorème se réfère au cas général, qui est déterminé par le théorème de Muavre-Laplace. Et le théorème indiqué, dans cette formulation, ne peut pas être un critère non ambigu pour le caractère aléatoire d'une série. Mais la fractalité, et dans ce cas, il est exprimé que des chaînes de longueur indiquée peuvent être combinées avec des chaînes de longueur plus longue, ne nous permet pas de rejeter ce théorème sans ambiguïté, car une inexactitude dans la formulation est possible. Un exemple est le fait que si pour une probabilité de 256 bits d'un nombre où la chaîne maximale de 8 bits est de 0,2444235, alors, conjointement avec d'autres séquences plus longues, la probabilité qu'un nombre de 8 bits soit présent dans un nombre est déjà - 0.490234375. Autrement dit, jusqu'à présent, il n'y a aucune possibilité sans équivoque de rejeter ce théorème. Mais ce théorème s'intègre assez bien dans un autre aspect, qui sera montré plus loin.
Application pratique
Regardons l'exemple présenté par l'utilisateur VDG:
«... Les branches dendritiques d'un neurone peuvent être représentées comme une séquence de bits. Une branche, puis le neurone entier, est déclenchée lorsqu'une chaîne de synapses est activée à n'importe quel endroit. Le neurone a pour tâche de ne pas répondre au bruit blanc, respectivement, la longueur minimale de la chaîne, pour autant que je m'en souvienne dans Numenta, est de 14 synapses dans le neurone pyramidal avec ses 10 mille synapses. Et selon la formule que nous obtenons: Log_ {2} 10000 = 13,287. Autrement dit, des chaînes de moins de 14 longueurs se produiront en raison du bruit naturel, mais n'activeront pas le neurone. C'est parfaitement bien .
"Nous allons construire un graphique, mais en tenant compte du fait qu'Excel ne considère pas les valeurs supérieures à 2 ^ 1024, nous nous limiterons au nombre de synapses 1023 et, en tenant compte de cela, nous interpolerons le résultat par commentaire, comme le montre la figure 18.

Fig. 18.
Il existe un réseau de neurones biologiques qui se déclenche lorsqu'une chaîne de m = log2N = 11 est compilée. Cette chaîne est une valeur modale et une valeur seuil, la probabilité, d'une sorte de changement dans la situation de 0,78 est atteinte. Et la probabilité d'erreur est de 1- 0,78 = 0,22. Supposons qu'une chaîne de 9 capteurs fonctionne, où la probabilité de déterminer l'événement est respectivement de 0,37, la probabilité d'erreur est de 1 - 0,37 = 0,63. Autrement dit, pour parvenir à une diminution de la probabilité d'erreur de 0,63 à 0,37, il faut que 3,33 chaînes de 9 éléments fonctionnent. La différence entre 11 et 9 éléments est du 2ème ordre, c'est-à-dire 2 ^ 2 = 4 fois, qui, s'ils sont arrondis à des entiers, puisque les éléments donnent une valeur entière, alors 3,33 = 4. Nous cherchons encore à réduire l'erreur lors du traitement d'un signal de 8- éléments, nous avons déjà besoin de 11 chaînes de déclenchement de 8 éléments. Je suppose que c'est un mécanisme qui vous permet d'évaluer la situation et de prendre une décision concernant la modification du comportement d'un objet biologique. Raisonnablement et assez efficacement, à mon avis. Et compte tenu du fait que nous savons de la nature qu'elle utilise les ressources le plus économiquement possible, l'hypothèse que le système biologique utilise ce mécanisme est justifiée. Et lorsque nous formons le réseau neuronal, nous réduisons en fait le risque d'erreur, car pour éliminer complètement l'erreur, nous devons trouver une relation analytique.
Nous passons à l'analyse des données numériques. Dans l'analyse des données numériques, nous essayons de choisir une dépendance analytique sous la forme y = f (xi). Et au premier stade, nous la trouvons. Après l'avoir trouvée, la série existante peut être représentée sous forme binaire, par rapport à l'équation de régression, où nous attribuons 1 à des valeurs positives et 0 à des valeurs négatives, puis nous analysons sur une série d'éléments identiques. Nous déterminons la plus grande, sur la longueur de la chaîne, la distribution des chaînes plus courtes.
Ensuite, nous passons au théorème d'Erdos-Renyi, il en résulte que lors de la réalisation d'un grand nombre de tests d'une valeur aléatoire, une chaîne d'éléments identiques doit être formée dans tous les registres du nombre généré, c'est-à-dire m = log2N. Maintenant, lorsque nous examinons les données, nous ne savons pas vraiment quel est le volume de la série. Mais si vous regardez en arrière, cette chaîne maximale nous donne des raisons de supposer que R est un paramètre caractérisant un champ de variable aléatoire, figure 19.
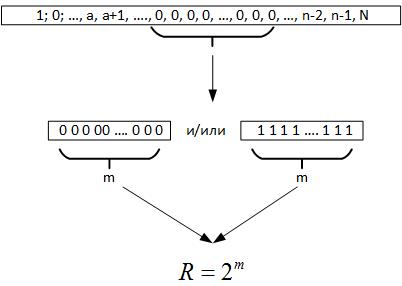
Fig. 19.
Autrement dit, en comparant R et N, nous pouvons tirer plusieurs conclusions:
- Si R <N, le processus aléatoire est répété plusieurs fois sur les données historiques.
- Si R> N, alors le processus aléatoire a une dimension supérieure aux données disponibles, ou nous avons mal déterminé l'équation de la fonction objectif.
Ensuite, pour le premier cas, nous concevons un réseau neuronal avec des capteurs de 2 ^ m, je suppose que nous pouvons ajouter une paire de capteurs pour capturer les transitions, et nous formons ce réseau sur des données historiques. Si le réseau à la suite de la formation n'est pas en mesure d'apprendre et produira le résultat correct avec une probabilité de 50%, cela signifie que la fonction objective trouvée est optimale et qu'il est impossible de l'améliorer. Si le réseau peut apprendre, nous améliorerons encore la dépendance analytique.
Si la dimension de la série est supérieure à la dimension d'une variable aléatoire, alors la propriété de fractalité de la variable aléatoire peut être utilisée, car toute série de taille m contient tous les sous-espaces de dimensions inférieures. Je suppose que dans ce cas, il est logique de former le réseau neuronal sur toutes les données, sauf les chaînes m.
Une autre approche de la conception des réseaux de neurones pourrait être la période de prévision.
En conclusion, il faut dire que, sur le chemin de cette publication, de nombreux aspects ont été découverts où la magnitude de la dimension d'une variable aléatoire et ses propriétés découvertes se sont croisées avec d'autres tâches dans l'analyse des données. Mais pour l'instant, tout cela est sous une forme très brute et sera laissé pour de futures publications.
Partie précédente:
Partie 1 ,
partie 2