Posit-arithmétique: vaincre un point flottant dans son propre champ. 2e partie

Partie 1

4. Comparaison quantitative des systèmes numériques

4.1. Précision décimale

La précision est l'opposé de l'erreur. Si nous avons une paire de nombres x et y (non nul et un signe), la distance entre eux par ordre de grandeur est $$$\ mid log_ {10} (x / y) \ mid$ ordres décimaux, il s'agit de la même mesure qui définit la plage dynamique entre le plus petit et le plus grand nombre positif représentable x et y. La distribution idéale de dix nombres entre 1 et 10 dans un système de nombres réels ne serait pas une distribution uniforme des nombres dans l'ordre de 1 à 10, mais exponentielle: $$ . Il s'agit de l'échelle de décibels utilisée par les ingénieurs depuis longtemps pour exprimer les relations, par exemple, 10 décibels est un rapport décuplé. 30db signifie coefficient $$ . Le rapport de 1 dB est un facteur d'environ 1,26, si vous connaissez la valeur avec une précision de 1 dB, vous avez une précision de 1 décimale. Si vous connaissez la valeur avec une précision de 0,1 db, cela signifie 2 signes de précision, etc. La formule de précision décimale est $$$log_ {10} (1 / \ mid log_ {10} (x / y) \ mid) = - log_ {10} (\ mid log_ {10} (x / y) \ mid)$ , où x et y sont soit des valeurs valides calculées à l'aide de systèmes d'arrondi, tels que ceux utilisés dans les formats float et posit, soit des limites supérieures et inférieures si des systèmes stricts utilisant des intervalles sont utilisés, ou des valeurs valides.

4.2. Définir des ensembles de comparaison flottants et positifs

Nous pouvons créer des modèles réduits de nombres flottants et positifs de 8 bits chacun. L'avantage de cette approche est que 256 valeurs sont un ensemble suffisamment petit pour que nous puissions le tester complètement et tout comparer $$ occurrences dans les tableaux pour les opérations d'addition, de soustraction, de multiplication et de division. Les nombres réels avec une précision de 1/4 ont un bit de signe, quatre bits de l'exposant et trois bits de la partie fractionnaire, et adhèrent à toutes les règles de l'IEEE 754. Le plus petit nombre positif (dénormalisé) est 1/1024, le plus grand positif est 240, la plage dynamique est asymétrique et égale 5.1 ordres décimaux.Les combinaisons de 14 bits représentent NaN.

Une position 8 bits comparable utilise es = 1, a une plage de nombres positifs de 1/4096 à 4096, une plage dynamique symétrique de 7,2 décimales. Il n'y a pas de valeurs NaN. Nous pouvons tracer des graphiques de précision décimale de nombres positifs dans les deux ensembles, comme le montre la fig. 7. Notez que les valeurs représentées par des nombres positifs ont une plage dynamique de deux ordres de grandeur plus grande que les nombres flottants et que la précision est identique ou supérieure pour toutes les valeurs, sauf celles où les nombres flottants sont proches du débordement ou de l'anti-débordement. L'indentation des graphiques pour les deux systèmes est une approximation logarithmique d'une fonction linéaire par morceaux. En nombres flottants, la précision ne diminue qu'à gauche, dans la zone proche de l'antipersonnalité, à droite, la fonction se détache, car viennent ensuite les valeurs de NaN. Les nombres positifs ont une fonction de précision décroissante plus symétrique autour des bords.


Fig. 7. Comparaison de la précision décimale des nombres flottants et positifs

4.3. Comparaison d'opérations sur un seul argument

4.3.1. Valeur inverse

Pour chaque valeur d'entrée x possible de la fonction 1 / x, le résultat peut correspondre exactement à une autre valeur dans l'ensemble donné, ou il peut être arrondi, dans ce cas, nous pouvons mesurer l'erreur décimale en utilisant la formule de la section 4.1, pour les nombres flottants, le résultat peut conduire à un débordement ou NaN. Voir fig. 8.



Fig. 8. Comparaison quantitative des nombres flottants et positifs lors du calcul de la valeur inverse

Les courbes sur le graphique de droite montrent l'ampleur de l'erreur dans le calcul de la valeur inverse, tandis que les nombres flottants peuvent entraîner NaN. Les nombres de positions sont supérieurs à flottants dans un grand nombre de cas, et cette supériorité est maintenue dans toute la gamme. Le calcul de l'inverse des nombres flottants dénormalisés provoque un débordement, ce qui conduit à une valeur d'erreur infinie, et, bien sûr, l'argument NaN donne l'inverse du NaN. Les nombres positifs sont fermés par rapport au calcul de la valeur inverse.

4.3.2. Racine carrée

La fonction racine carrée n'entraîne ni débordement ni anti-débordement. Pour les arguments négatifs et pour NaN, le résultat sera NaN. Rappelons que nous avons un «modèle à l'échelle» des nombres flottants et positifs, les avantages de posit augmentent avec l'augmentation de la précision des données. Pour les valeurs flottantes et positives de 64 bits, l'erreur de position sera d'environ 1/30 de l'erreur de flottement, au lieu de 1/2.

4.3.3. Carré

Une autre opération unaire courante est $$$x ^ 2$ . Les débordements et les anti-débordements sont courants lors de l'équerrage d'un flotteur. Pour près de la moitié d'un flottant, la mise au carré ne produit pas de résultat significatif, tandis que la mise au carré du nombre de posit dans un carré donne toujours le nombre posit (un carré d'infini non signé est un infini non signé).


Fig. 9. Comparaison quantitative des nombres flottants et positifs lors du calcul $$$\ sqrt x$


Fig. 10. Comparaison quantitative des nombres flottants et positifs lors du calcul $$$x ^ 2$

4.3.4. Logarithme en base 2

Nous avons également effectué une comparaison pour couvrir la fonction de logarithme de base 2, c'est-à-dire le pourcentage de cas dans lesquels $$$log_2 (x)$ peut être représenté avec précision, et s'il ne peut pas être représenté avec précision, combien de décimales nous perdons. Les nombres flottants ont le seul avantage dans ce cas: ils peuvent être utilisés pour représenter $$$log_2 (0)$ comment $$$- \ infty$ et $$$log_2 (\ infty)$ comment $$$\ infty$ , mais cela est plus que compensé par un grand dictionnaire de puissances entières de deux pour les nombres positifs.


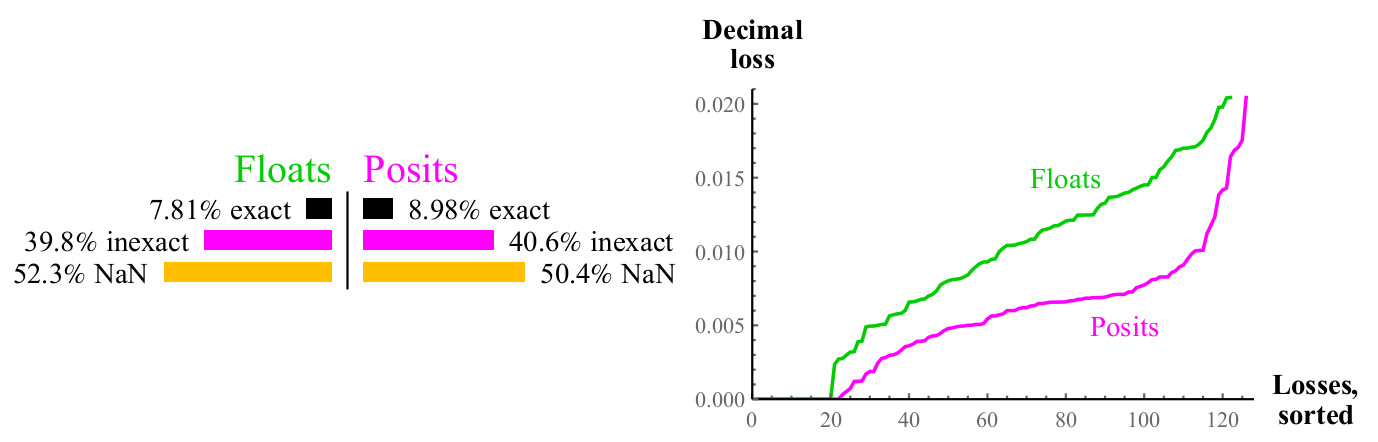
Fig. 11. Comparaison quantitative des nombres flottants et positifs lors du calcul $$$log_2 (x)$

Le graphique est similaire à celui de la racine carrée, environ la moitié des cas donnent NaN dans les deux cas, mais les nombres positifs ont la moitié de la perte de précision décimale. Si vous pouvez calculer $$$log_2 (x)$ , il vous suffit de multiplier le résultat par un facteur d'échelle pour obtenir $$$ln (x)$ ou $$$log_ {10} (x)$ ou logarithme pour toute autre raison.

4.3.5. Exposant $$$2 ^ x$

De même, si vous pouvez calculer $$$2 ^ x$ , vous pouvez facilement utiliser le facteur d'échelle pour obtenir $$$e ^ x$ ou $$ etc. Les numéros de poste ont une exception, $$$2 ^ x$ est égal à NaN lorsque l'argument est $$$\ pm \ infty$ .


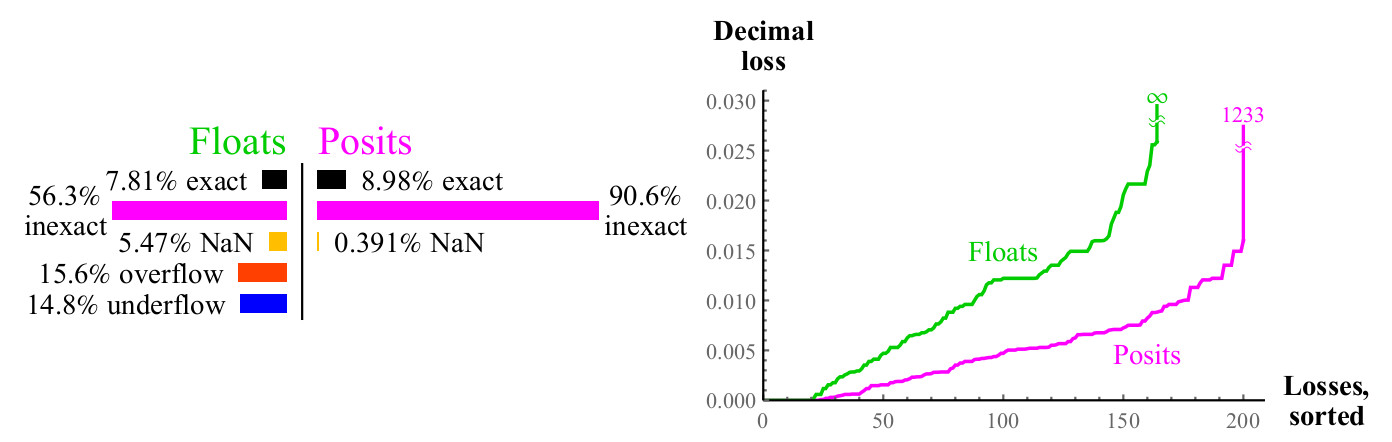
Fig. 12. Comparaison quantitative des nombres flottants et positifs lors du calcul $$$2 ^ x$

La perte décimale maximale pour les nombres positifs peut sembler importante car $$$2 ^ {maxpos}$ sera arrondi à maxpos. Dans cet exemple, seul un petit nombre d'erreurs sont aussi importantes que $$$log_ {10} (24096) \ environ1233$ ordres décimaux. Décidez ce qui est le mieux: perdre plus d'un millier de décimales ou perdre un nombre infini de décimales? Si vous ne pouvez pas utiliser des nombres aussi grands, les nombres positifs sont toujours gagnants, car les erreurs avec de petites valeurs sont bien meilleures. Dans tous les cas, lorsque vous perdez un grand nombre de décimales lorsque vous utilisez des nombres positifs, l'argument d'entrée va bien au-delà de ce que les nombres flottants peuvent même exprimer . Les graphiques montrent comment les nombres positifs sont plus stables en termes de plage dynamique dans laquelle le résultat a du sens et sont supérieurs en précision dans cette plage.

Pour les opérations unaires ordinaires $$$1 / x, \ sqrt x, x ^ 2, log_2 (x)$ et $$$2 ^ x$ , les nombres positifs sont complètement et invariablement plus précis que les nombres flottants avec le même nombre de bits, et produisent des résultats significatifs dans une large plage dynamique. Nous tournons maintenant notre attention vers quatre opérations arithmétiques élémentaires qui ont deux arguments: addition, soustraction, multiplication et division.

4.4. Comparaison des opérations de deux arguments

Nous pouvons utiliser le modèle à l'échelle d'un système numérique pour étudier les opérations arithmétiques de deux arguments, tels que l'addition, la soustraction, la multiplication et la division. Afin de visualiser 65536 résultats, nous créons un «graphique de couverture» de 256 * 256, qui montre clairement quelle proportion des résultats est précise, inexacte, provoque un débordement, un anti-débordement ou NaN.

4.4.1. Addition et soustraction

Depuis $$$x - y = x + (- y)$ fonctionne très bien pour float et posit, il n'est pas nécessaire d'étudier la soustraction séparément. Pour l'opération d'addition, nous calculons la valeur exacte $$$z = x + y$ et comparez-le avec le montant retourné dans chacun des systèmes de numérotation. Il peut arriver que le résultat soit inexact, alors il doit être arrondi au nombre fini non nul le plus proche, débordement ou anti-débordement, ou une incertitude de la forme peut se produire $$$\ infty- \ infty$ ce qui se traduit par NaN. Chacun de ces cas est marqué en couleur, et nous pouvons couvrir l'ensemble du tableau d'addition en un coup d'œil. Dans le cas de l'arrondissement des résultats, la couleur passe du noir (valeur exacte) au violet (valeur exacte pour posit et float). Fig. 13 montre à quoi ressemble le graphique de couverture des nombres flottants et unum. Comme pour les opérations unaires, mais ayant beaucoup plus de points, nous pouvons tirer des conclusions sur la capacité de chaque système numérique à donner des réponses significatives et précises:


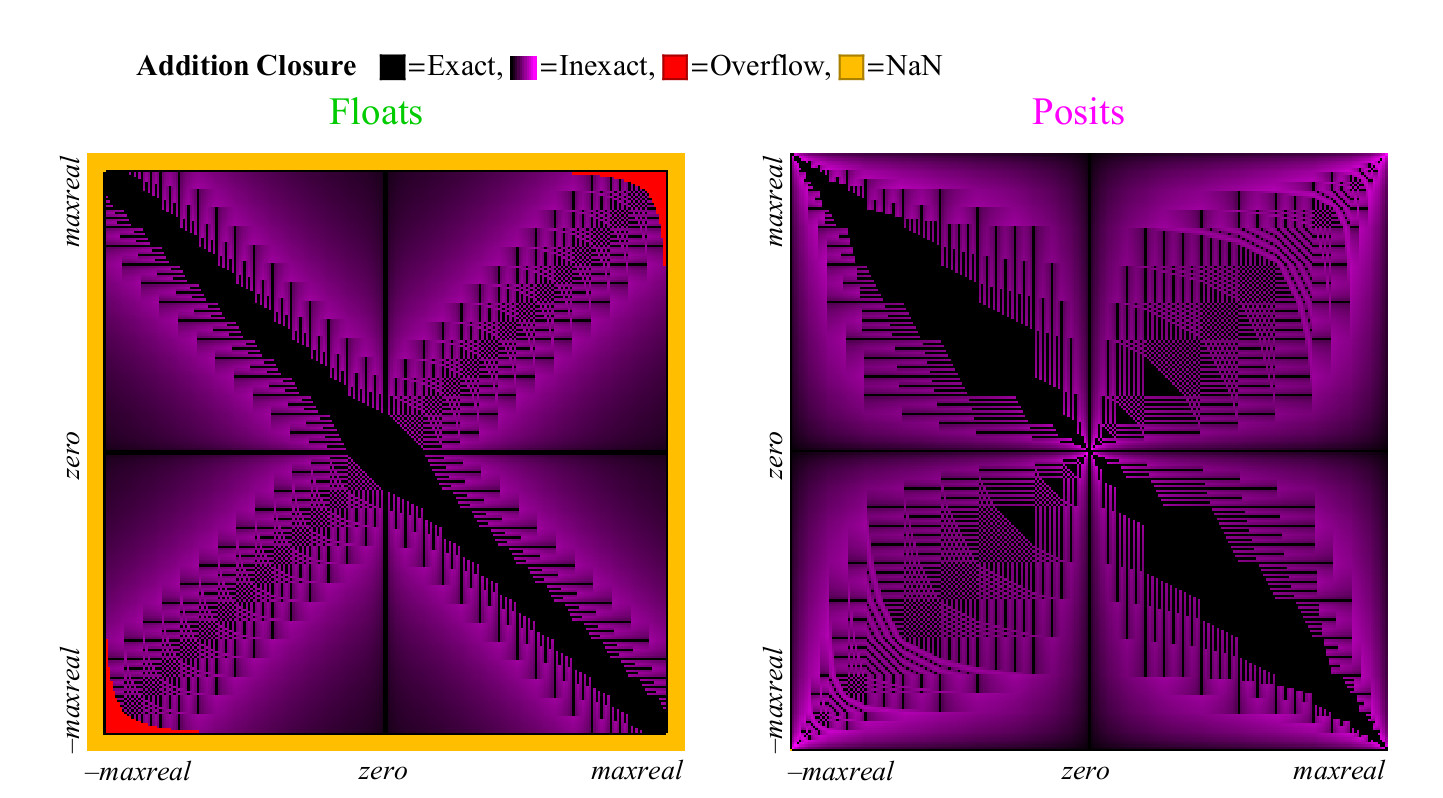
Fig. 13. Graphique de couverture complète pour ajouter des nombres flottants et positifs


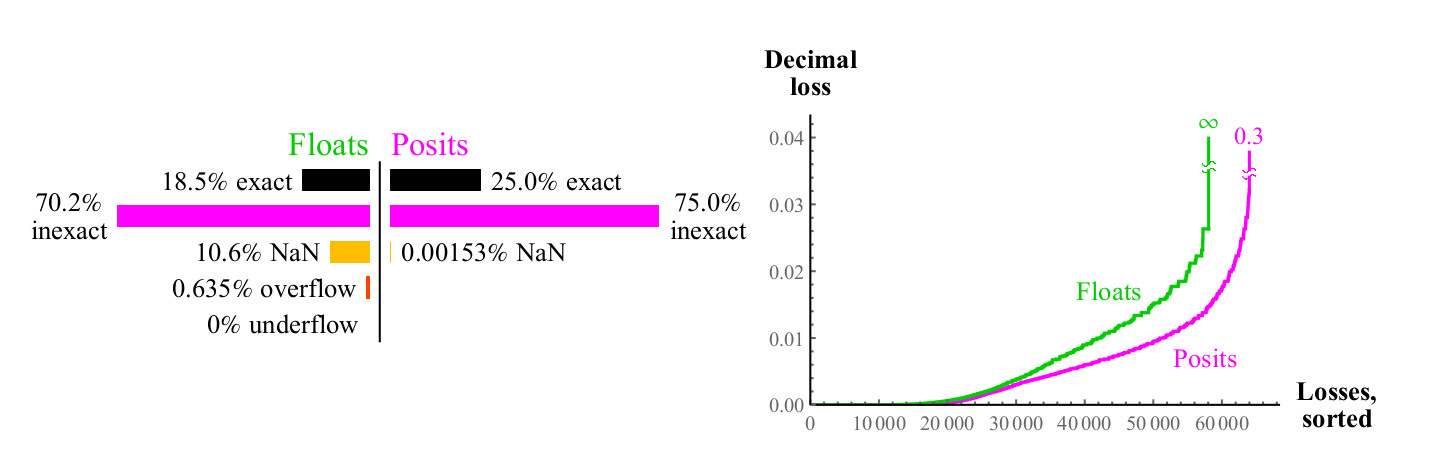
Fig. 14. Comparaison quantitative des nombres flottants et positifs pour l'addition

À première vue, il devient évident que posit a significativement plus de points sur le graphique d'addition auxquels le résultat est précis. La large bande diagonale noire sur le graphique de couverture du flottant est beaucoup plus large qu'elle ne le sera pour une plus grande précision, car elle représente une zone numérique dénormalisée dans laquelle les nombres flottants sont espacés à intervalles égaux, comme les nombres à virgule fixe, ces nombres constituent une grande proportion du nombre total uniquement dans le cas de nombres à 8 bits.

4.4.2. Multiplication

Nous utilisons une approche similaire pour comparer la multiplication des nombres flottants et positifs. Contrairement à l'addition, la multiplication peut provoquer un anti-débordement des nombres flottants. «Anti-débordement progressif», la zone que vous pouvez voir au centre de la Fig. 15. à gauche. ( ce qui signifie des nombres dénormalisés. environ transl. ) Sans cette zone, la zone bleue anti-débordement aurait une forme de diamant. Le graphique de multiplication des nombres positifs est moins coloré, ce qui est mieux. Seuls deux pixels sont mis en surbrillance en tant que NaN, près de l'endroit où se trouve le point zéro des axes (les pixels sont les plus à gauche au centre verticalement et en bas au centre horizontalement. Env. Transl. ) Il y a des résultats de multiplication $$$\ pm \ infty \ cdot 0 = NaN$ . Les nombres flottants ont plus de cas où le produit est précis mais à un prix terrible. Comme le montre la figure 15, près de 1/4 de tous les produits flottants entraînent un débordement ou un anti-débordement, et cette fraction ne diminue pas avec l'augmentation de la précision du flotteur.


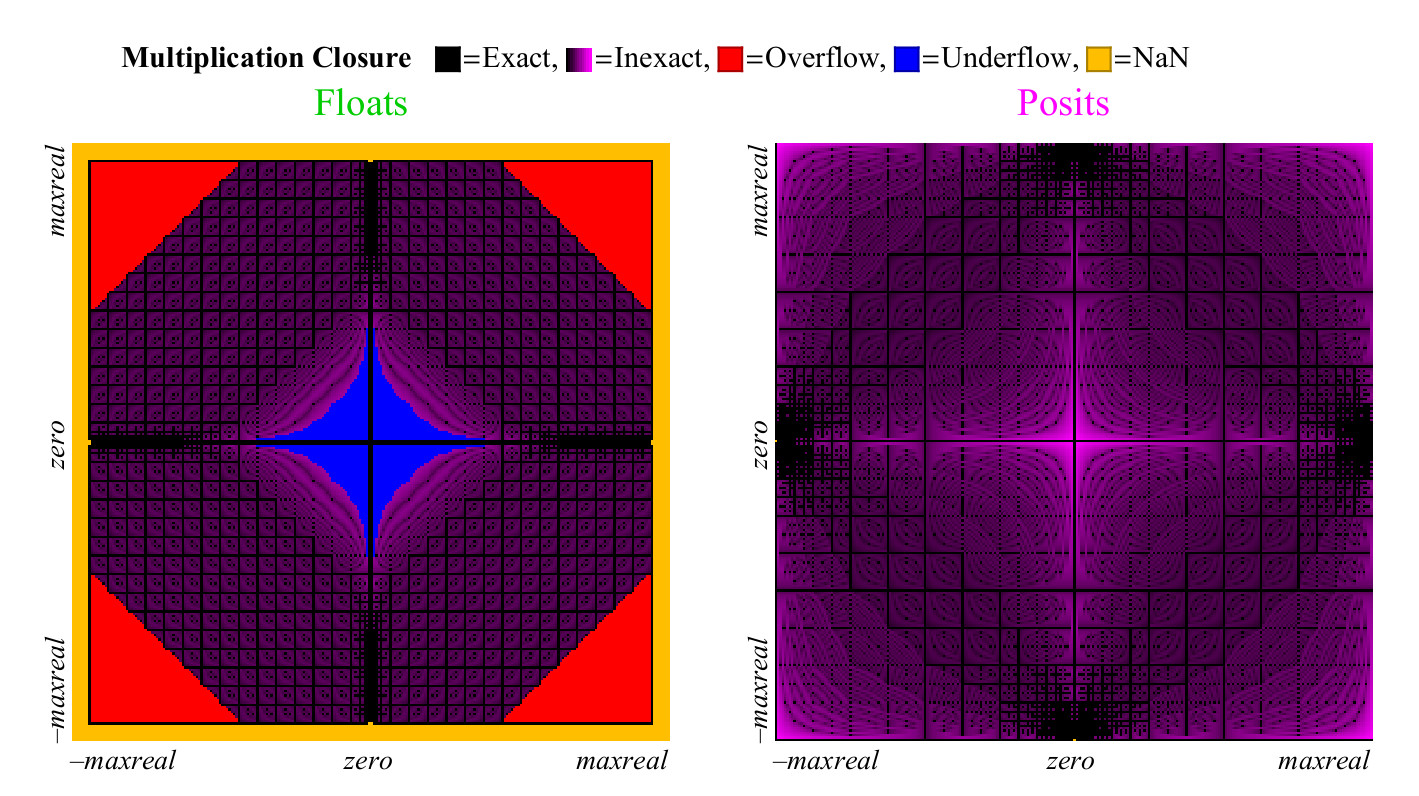
Figure 15. Graphique de couverture complète pour multiplier les nombres flottants et positifs

Le pire cas d'arrondi pour les nombres positifs se produit lorsque $$$maxpos \ fois maxpos$ qui est à nouveau arrondi à maxpos. Pour de tels cas (très rare), l'erreur est de 3,6 ordres décimaux. Comme le graphique de la fig. 16, les nombres positifs sont nettement meilleurs que flottants, minimisent l'erreur de multiplication.


Fig. 16. Comparaison quantitative des nombres flottants et positifs pour la multiplication

Le graphique de couverture pour l'opération de division est similaire au graphique pour la multiplication, mais les zones sont permutées, pour économiser de l'espace, il n'est pas affiché ici. Les indicateurs quantitatifs pour la division sont presque les mêmes que pour la multiplication.

4.5. Comparaison des nombres flottants et positifs pour évaluer les expressions

4.5.1. Test «budget de précision 32 bits»

Les tests sont généralement effectués sur la base de la durée d'exécution minimale et ne donnent souvent pas une image complète de la précision du résultat. Un autre type de test est celui dans lequel nous fixons le budget de l'erreur, c'est-à-dire le nombre de bits par variable, et essayons d'obtenir la précision décimale maximale en conséquence. Voici un exemple d'une expression que nous pouvons utiliser pour comparer des systèmes numériques avec un budget de 32 bits par nombre:

$$

$$X = \ left (\ dfrac {27/10-e} {\ pi - (\ sqrt 2+ \ sqrt 3)} \ right) ^ {67/16} = 302.8827196 \ dotsb$$

La règle est que nous commençons par la meilleure représentation des nombres $$$\ pi$ et $$$e$ possible dans chacun des systèmes numériques, et des représentations de tous les entiers indiqués, et nous voyons combien de chiffres décimaux correspondent à la vraie valeur de X après avoir effectué neuf opérations dans l'expression. Nous mettrons en surbrillance les mauvais numéros en orange .

Malgré le fait que les nombres flottants IEEE 32 bits aient une précision décimale, qui varie de 7,3 à 7,6 ordres décimaux, l'accumulation d'erreurs d'arrondi dans le calcul de X donne une réponse de 302. 912 , qui n'a que trois chiffres valides. C'est l'une des raisons pour lesquelles les utilisateurs ressentent le besoin d'utiliser float 64 bits partout, car même les expressions simples risquent de perdre tellement en précision que le résultat peut être inutile.

Les nombres positifs 32 bits ont une précision décimale variable, qui varie entre 8,2 et 8,5 ordres décimaux pour les nombres avec une valeur absolue d'environ 1. Lors du calcul de X, ils nous donnent une réponse de 302,882 31 , qui a deux fois plus de chiffres significatifs. N'oubliez pas non plus que les nombres positifs 32 bits ont une plage dynamique de plus de 144 décimales et que les flottants 32 bits ont une plage dynamique beaucoup plus petite de 83 bits. Par conséquent, la précision supplémentaire du résultat n'est pas obtenue en rétrécissant la plage dynamique.

4.5.2. Test quadruple: le problème du triangle mince de Goldberg

Il y a un problème classique de "triangle mince" [1]: trouver l'aire d'un triangle avec les côtés a , b , c lorsque deux des côtés b et c ne sont que 3 unités du chiffre le moins significatif (Unités à la dernière place, ULP) plus longues que la moitié de la longue côtés (Fig.17).


Fig. 17. Le problème du triangle fin de Goldberg

La formule classique pour la zone A utilise la variable intermédiaire s:

$$

$$s = \ frac {a + b + c} 2; A = \ sqrt {s (s-a) (s-b) (s-c)}$$

Le danger dans cette formule est que s est très proche de la valeur de a , et le calcul $$$(s-a)$ augmente considérablement l'erreur d'arrondi. Essayons les nombres flottants IEEE 128 bits (avec une précision quadruple) pour lesquels $$$a = 7, b = c = 7/2 + 3 \ fois 2 ^ {- 111}$ . (Si vous prenez l'année-lumière comme unité de mesure, le côté court sera plus long que la moitié du côté long par seulement 1/200 du diamètre du proton. Mais cela fait un triangle de la hauteur de la porte en haut.) Nous calculons également la valeur de A en utilisant des nombres positifs de 128 bits ( es = 7). Voici les résultats:

$$$$ afficher $$ \ begin {matrix} \ textrm {True value:} & 3.14784204874900425235885265494550774498 \ dots \ times 10 ^ {- 16} \\ \ textrm {float IEEE 128 bits:} & 3. \ color {orange} { 63481490842332134725920516158057682788} \ dots \ times 10 ^ {- 16} \\ \ textrm {position 128 bits:} & 3.147842048749004252358852654945507744 \ color {orange} {39} \ dots \ times 10 ^ {- 16} \ end {matrix} $$ afficher $$

Les nombres de position ont jusqu'à 1,8 décimales de précision supérieure à un quadruple flotteur de précision dans une large plage dynamique: de $$$2 \ fois 10 ^ {- 270}$ avant $$ . Cela suffit pour éviter les conséquences catastrophiques de l'augmentation de l'erreur dans ce cas particulier. Il est également intéressant de noter que la réponse au format posit sera plus précise que dans le format float, même si à la fin nous la convertissons en posit 16 bits.

4.5.3. La solution de l'équation quadratique

Il existe une astuce classique conçue pour éviter les erreurs d'arrondi lors du calcul des racines $$$r_1$ , $$$r_2$ équations $$$ax ^ 2 + bx + c = 0$ en utilisant la formule habituelle $$$r_1, r_2 = (- b \ pm \ sqrt {b ^ 2-4ac}) / (2a)$ lorsque b est beaucoup plus grand que a et c , ce qui conduit à la disparition des chiffres à gauche, car $$$\ sqrt {b ^ 2-4ac}$ très proche de b . Mais au lieu de forcer les programmeurs à mémoriser des astuces mystiques, il pourrait être préférable pour posit de sécuriser le calcul en utilisant une formule simple à partir d'un didacticiel. Mettez $$$a = 3, b = 100, c = 2$ et comparer le résultat au format float et posit 32 bits.

Tableau 5. La solution de l'équation quadratique


Racine instable numériquement - $$$r_1$ , mais notez que la position 32 bits donne 6 chiffres corrects au lieu de 4 pour float.

4.6. Comparaison des flotteurs et des systèmes Posit pour le test LINPACK classique

Pendant longtemps, la principale méthode d'évaluation des superordinateurs était de résoudre $$$n \ fois n$ systèmes d'équations linéaires $$$\ mathbf Axe = b$ . A savoir, le test remplit la matrice A avec des nombres pseudo-aléatoires de 0 à 1, et le vecteur b avec les sommes des lignes A. Cela signifie que la solution x est un vecteur composé d'unités. Le test calcule le taux de déduction $$$\ | \ mathbf Axe-b \ |$ pour vérifier l'exactitude, bien qu'il n'y ait pas de nombre fixe de chiffres qui doivent être vrais dans la réponse. Une perte typique de plusieurs chiffres de précision est typique pour le test, et des flottants 64 bits sont généralement utilisés (pas nécessairement IEEE). Initialement, le test prévoyait n = 100, mais cette taille était trop petite pour les supercalculateurs les plus rapides, donc n a été augmenté à 300, puis à 1000, et enfin (du premier auteur), le test est devenu évolutif et donne le nombre d'opérations par seconde, basé sur le fait que le test effectue $$$\ frac {2} {3} n ^ 3 + 2n ^ 2$ opérations de multiplication et d'addition.

En comparant posit et float, nous avons noté un léger inconvénient du test: la réponse dans le cas général n'est pas une séquence d'unités, en raison d'erreurs d'arrondi dans les sommes en lignes. Une telle erreur peut être éliminée si nous trouvons comment les occurrences dans A contribuent à 1 bit, ce qui est en dehors de la plage de précision possible, et définissons ce bit sur 0. Cela nous donnera l'assurance que la somme de la ligne A est représentable sans arrondi et que la réponse est x est en fait un vecteur composé d'unités. Pour la version originale de la tâche, avec une taille de 100x100, le flottant IEEE 64 bits donne une réponse de ce type:

0,9999999999999 633626401873698341660201549530029296875
1.00000000000000 11102230246251565404236316680908203125
$$$\ vdots$
1.0000000000000 22648549702353193424642086029052734375

Aucun des 100 nombres n'est vrai; ils sont proches de 1 mais jamais égaux à 1. Avec des nombres positifs, nous pouvons faire une chose merveilleuse. En utilisant des nombres positifs de 32 bits et le même algorithme, nous calculons le résidu $$$r = \ mathbf Axe - b$ l'utilisation de l'opération de fusion est un produit scalaire. Décidez ensuite $$$\ mathbf Axe '= r$ (en utilisant déjà traité $$$\ mathbf A$ ) et utilisation $$$x '$ pour correction: $$$x \ leftarrow x-x '$ . Le résultat est la réponse d'une précision sans précédent pour le test LINPACK: $$$\ {1, 1, ..., 1 \}$ .Les règles LINPACK peuvent-elles interdire l'utilisation d'un nouveau type de nombres 32 bits, dont l'utilisation permet d'obtenir un résultat parfait avec une erreur nulle, ou continuer à insister sur l'utilisation d'un flottant 64 bits, ce qui ne le permet pas? Cette décision sera prise par les responsables de ce test. Pour ceux qui ont besoin de résoudre des systèmes d'équations linéaires pour résoudre des problèmes réels, plutôt que de comparer la vitesse des superordinateurs, posit offre des avantages étonnants.

5. Conclusion

Posit bat le flotteur dans son propre jeu: avec lui, vous pouvez effectuer des calculs et réduire les erreurs d'arrondi. Les nombres de positions ont une plus grande précision, une plus grande plage dynamique et une plus grande couverture. Ils peuvent être utilisés pour obtenir de meilleurs résultats qu'un flotteur de la même profondeur de bits, ou (ce qui peut être un avantage concurrentiel encore plus grand), les mêmes résultats avec une profondeur de bits inférieure. Étant donné que la bande passante du système est limitée, l'utilisation d'opérandes plus petits signifie une vitesse plus rapide et une consommation d'énergie inférieure.
Puisqu'ils fonctionnent comme un flotteur et non comme un système d'intervalles, ils peuvent être considérés comme un remplacement direct du flotteur, comme cela a été démontré ici. Si l'algorithme utilisant float réussit les tests et que le temps et la stabilité sont «assez bons», alors cela fonctionnera encore mieux avec posit. Les opérations fusionnées disponibles dans posit fournissent un outil puissant pour empêcher l'accumulation d'erreurs d'arrondi et, dans certains cas, vous permettent d'utiliser en toute sécurité des nombres positifs 32 bits au lieu de flottants 64 bits dans les applications qui nécessitent des performances élevées. En général, cela augmentera les performances des applications de 2 à 4 fois, réduira la consommation d'énergie, économisera de l'énergie et réduira le coût du stockage des données. Le support matériel nous donnera l'équivalent d'une ou deux étapes de la loi de Moore,sans avoir besoin de réduire la taille du transistor ou d'augmenter le coût. Contrairement au float, le système posit offre une reproductibilité bit par bit des résultats sur différents systèmes, éliminant le principal inconvénient de la norme IEEE 754. Les nombres posit sont plus simples et plus élégants que le float, et réduisent la quantité d'équipement pour les supporter. Bien que les nombres flottants soient désormais omniprésents, les nombres positifs pourraient bientôt les rendre obsolètes.

Références:

1. David Goldberg. Ce que tout informaticien devrait savoir sur l'arithmétique à virgule flottante.
ACM Computing Surveys (CSUR), 23 (1): 5–48, 1991. DOI: doi: 10.1145 / 103162.103163.
2. John L. Gustafson. La fin de l'erreur: Unum Computing, volume 24. CRC Press, 2015.
3. John L Gustafson. Au-delà de la virgule flottante: arithmétique informatique de nouvelle génération. Séminaire de Stanford: https://www.youtube.com/watch?v=aP0Y1uAA-2Y , 2016. transcription complète
disponible sur http://www.johngustafson.net/pdfs/DebateTranscription.pdf .
4. John L. Gustafson. Une approche radicale du calcul avec des nombres réels. Supercomputing
Frontiers and Innovations, 3 (2): 38–53, 2016. doi: http://dx.doi.org/10.14529/jsfi160203.
5. John L. Gustafson. Le grand débat @ ARITH23. https://www.youtube.com/watch?v=
KEAKYDyUua4 , 2016. transcription complète disponible sur http://www.johngustafson.net/pdfs/
DebateTranscription.pdf .
6. Ulrich W Kulisch et Willard L Miranker. Une nouvelle approche du calcul scientifique, volume 7. Elsevier, 2014.
7. Plus de sites. Norme IEEE pour l'arithmétique à virgule flottante. IEEE Computer Society, 2008.
DOI: 10.1109 / IEEESTD.2008.4610935.
8. Isaac Yonemoto. https://github.com/interplanetary-robot/SigmoidNumbers