Il se trouve que la science se développe de façon inégale et, par conséquent, dans notre vie d'aujourd'hui, pour ainsi dire, il y a une place pour la réussite. Un exploit, bien sûr, scientifique, mais qui n'en est pas moins significatif. Et maintenant, lecteurs, vous avez la possibilité de voir le lieu de l'exploit, les prix officiels de son paiement (comme c'est la coutume dans les pays qui se disent civilisés), et même de tenter votre chance vous-même. Eh bien, en même temps, au moins certains d'entre vous ressentiront le charme de trouver des perles dans des choses assez ordinaires.
De plus, dans plusieurs séries, une histoire sera suivie sur les choses qui sont accessibles à tout diplômé du secondaire (et même à de nombreux écoliers). Il n'y aura aucune preuve, car ils sont souvent évidents, et s'ils étaient présentés ici, ils augmenteraient non seulement le volume, mais effrayeraient également de nombreux lecteurs.
Première série
Il y avait d'abord des étoiles. Il y avait un processus de jouer avec eux, de regarder et de sentir, de se jeter et d'observer un chemin de chute brillant. Les étoiles étaient des motifs. Et les chiffres étaient le bac à sable. Les chiffres ont tourné du côté neuf, et une autre étoile est apparue dans les écarts entre eux. Son éclat fit signe et, surtout, ne brûla pas, mais se laissa toucher, ramasser, puis leur fit signe pour laisser une trace étincelante de poussière d'étoile. Mais ensuite, les stars sont devenues familières et il ne leur restait plus qu'un travail à faire. Et puis une idée est venue.
L'idée était simple - vous pouvez gagner de l'argent dessus. Et oui, c'était vraiment motivé. Mais cela n'a pas grandi ensemble. C'était amusant, il y avait des étoiles régulières qui brillaient d'une nouvelle manière, il y avait du plaisir et il y avait du progrès. Ce n'est qu'à la fin qu'une forêt est apparue, une forêt continue d'arbres brillants. Et j'étais faible, je ne pouvais pas trier cette taïga à la recherche de la vraie lumière, car il y a des millions d'arbres, et je suis seul. Par conséquent, je vous suggère de regarder les étoiles, et si elles sont intéressantes, vous pouvez gagner 400 000 $, mais la vérité est qu'il y en a un «mais» - dans la forêt, vous devez être en mesure de choisir le bon chemin.
À l'approche des étoiles
Qu'est-ce qu'un numéro? D'une part, c'est un produit de notre esprit sombre, introuvable dans la nature. Mais d'un autre côté, une telle abstraction nous permet de modéliser de nombreux processus que nous observons tous de même nature. Seul le modèle n'est pas égal au phénomène observé. Encore une fois, nous avons affaire à l'adaptation à nos modestes capacités de décrire la nature. C'est bon? En termes de précision, la description n'est pas très bonne. Non pas parce que quelqu'un peut ne pas avoir suffisamment de décimales, mais parce qu'un phénomène mal modélisé peut nous surprendre grandement quand il s'avère que le modèle manque d'une ou l'autre caractéristique spécifique qui est présente dans la réalité et peut même parfois sembler un peu ennuyeux naturalistes inattentifs sur la tête.
À la lumière de ce qui précède, essayons de nous renseigner sur l'exhaustivité du fondement de toute modélisation - l'exhaustivité de la compréhension du concept de nombre. Juste un certain nombre, juste des connaissances à ce sujet, établies dès la petite enfance, il semble - eh bien, quoi d'autre pourrait-il être? Mais juste là, nous pouvons trouver l'abîme. Oui, celui qui n'a pas de fond et qui est plein d'étoiles.
Il n'y a pas de chiffres dans la nature. Mais dans la nature, vous pouvez voir la relation. Le nuage est plus grand (plus long / plus large / plus épais / comme_vous_autre_will_be_becoming) que l'autre nuage, ce qui signifie qu'il y a une place pour la corrélation. Mais le ratio n'a pas non plus de chiffres. Il n'y a que deux nuages, un de plus, l'autre moins, et il y a leur rapport. Bien que oui, le ratio a également été inventé par l'homme. Par conséquent, on peut se demander - à quoi sert-il? L'avantage est le suivant: le concept de corrélation a une longueur d'avance sur le concept de nombre. Au début, il y avait un ratio, et ce n'est qu'ensuite qu'un nombre est apparu. Plus précisément - nombres fractionnaires. Par conséquent, en comprenant la relation, nous comprendrons les chiffres.
Comment les nombres fractionnaires sont-ils obtenus? Très simple - de la nécessité de modéliser la corrélation. Au début, il y avait des proportions de marches et de côtés de terre, des moutons d'un propriétaire à des moutons d'un autre, du poids d'une pastèque au poids d'un autre. Dans tous ces cas, il fallait en quelque sorte exprimer la différence. Mais la différence n'était pas strictement divisée par le nombre de marches ou par la taille de la pastèque voisine. Au début, ils ont appris à exprimer la différence en les divisant en unités de mesure plus petites (des coudes ont été ajoutés aux marches et des doigts ont été ajoutés aux coudes). Mais la science ne s'est pas arrêtée et a exigé une précision toujours plus grande. En conséquence, tout le monde était d'accord sur l'uniformité, oubliant les doigts, les coudes, les marches et les autres livres sterling. L'uniformité est exprimée en nombre.
Comment corréler deux segments si l'un d'eux ne rentre pas dans l'autre un nombre entier de fois? Vous pouvez mesurer avec vos doigts, mais il sera plus précis de prendre un segment plus petit comme unité de mesure et de le diviser en parties identiques. Avec ces parties, vous pouvez mesurer cette partie d'un segment plus grand qui n'est pas mesurée par l'ensemble du segment plus petit. Mais alors une nouvelle partie du segment plus grand apparaît, qui n'est plus mesurable par les parties sélectionnées. Nous appliquons la récursivité et divisons à nouveau les pièces déjà cassées en composants encore plus petits. Nous les mesurons auparavant incommensurables. Et encore une fois, nous obtenons un reste incommensurable. Divisez à nouveau les parties, mesurez à nouveau. Encore une fois, nous obtenons le reste. Mais vous pouvez vous ennuyer!
En conséquence, les gens ont eu l'idée d'arrondir et ont cessé de diviser l'unité de mesure. Autrement dit, les gens ont noté la précision (ils disent que c'est suffisant). Mais la nature ne pardonne pas les inexactitudes dans la modélisation.
Comment les ratios sont-ils modélisés aujourd'hui? Ils sont modélisés en utilisant la classification des nombres fractionnaires. La classification est la suivante: il y a des nombres entiers et des nombres fractionnaires. Les entiers sont encore instables, mais les fractions sont divisées en fractions finies et infinies. Pour l'instant, nous oublions également les derniers. L'infini est divisé en rationnel et irrationnel. Nous oublions généralement la première partie. Les irrationnels sont divisés en algébriques et transcendantaux. Tout, plus de divisions. Mais pour plus de clarté, nous donnons une classification sous forme d'image:
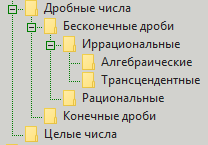
Pourquoi cette classification est-elle mauvaise? Elle n'est pas si mal. Elle, comme disait Winnie l'Ourson, est bonne, mais en quelque sorte boiteuse ... Autrement dit, il est clair qu'avec la précision de l'expression des valeurs, elle ne va pas bien à cause des infinis. Mais il y a un autre côté à la médaille. Ce côté (dans ce contexte) est appelé «divisibilité». Nous ne pouvons pas séparer précisément deux nombres (l'un sur l'autre) car nous nous appuyons sur l'infini. Mais d'un autre côté, nous nous intéressons à des phénomènes du monde des nombres comme la simplicité et le nombre de diviseurs qui éliminent l'infini lorsqu'ils apparaissent. Les nombres premiers constituent la base de la série de nombres entiers. Et ces numéros importants (y compris, par exemple, pour le confort lors du paiement à distance de services) dépendent fortement de l'opération de division. Et la division nous donne souvent des fractions. Et les fractions nous donnent des nombres fractionnaires. Eh bien, pour les nombres fractionnaires, quelqu'un nous a donné la classification donnée précédemment de fini, infini, rationnel, irrationnel, algébrique et transcendantal. Mais cette classification nous donne-t-elle la possibilité de trouver des réponses aux questions sur les chiffres? Par exemple, sur les mêmes simples? Ou fractionnaire? Il semble donner, mais pas autant que nous le souhaiterions.
Prenez des nombres premiers. Aujourd'hui, les nombres premiers maximaux sont essentiellement recherchés. Autrement dit, ils prennent le numéro de candidat, puis vérifient si c'est simple ou non. Les candidats obtiennent des nombres simplement - si vous connaissez la méthode de vérification de la simplicité pour une certaine classe de nombres, alors voici la liste des candidats sous la forme de représentants de la classe, qu'ils vont stupidement dans une rangée, vérifiant chaque numéro en commençant, bien sûr, par de petites valeurs. Et jusqu'à présent, ils sont arrivés à des nombres de l'ordre de deux au degré de quatre-vingts millions. C'est un nombre de près de vingt-cinq millions de décimales. En principe, cela semble impressionnant. Mais qu'est-ce qui nous empêche de rappeler le slogan «plus haut, plus loin, plus vite»?
Fondamentalement, nous sommes entravés par un manque de compréhension. Oui, notre modèle du phénomène appelé «nombre» est incomplet. Et oui, la partie du modèle, appelée "division", est incomplète au plus haut point. Par conséquent, quatre-vingt millions d'unités de mémoire informatique est la limite pour l'humanité. Pourquoi des unités? Parce qu'il ressemble aux plus grands nombres premiers. Ce sont des unités, mais en notation binaire. Pour eux, il y a le test de Luc-Lemer, qui nous montre un nombre simple ou un composé. Et ce test nécessite des années de travail d'un cœur de processeur pour vérifier un nombre candidat de quatre-vingt millions d'unités binaires. Quatre-vingt mégaoctets seulement, ou dix mégaoctets, et l'humanité n'est plus en mesure d'aller plus loin. Qu'est-ce que dix mégaoctets? C'est un sou, c'est une bagatelle, ce n'est presque rien pour les ordinateurs modernes. Mais le test dure depuis des années. Par conséquent, vous devez l'exécuter sur des millions d'ordinateurs sur lesquels les bénévoles installent le programme approprié, et par conséquent vérifier un numéro de candidat pendant un certain nombre de secondes (et ce s'il y a beaucoup de bénévoles). Mais le problème est qu'il y a beaucoup de numéros de candidats et qu'il faut donc plusieurs mois pour trouver le prochain nombre premier. Et avec une telle délibération, on peut s'attendre à ce que le mouvement de jusqu'à des centaines de millions d'unités binaires ne prenne que dix ans.
Est-il possible d'accélérer le processus? Tu peux. Mais une meilleure compréhension est nécessaire. Par exemple - comment réduire le temps de tester chaque numéro? Jusqu'à présent, une telle diminution est obtenue en massant le fer. Ou la deuxième option - vous pouvez offrir un test de simplicité plus rapide. Mais avec cela depuis environ 100 ans, peu de choses ont changé. Et pourtant, si vous le comprenez, alors peut-être que cela fonctionnera avec nous. Il suffit de comprendre les bases.
Étoiles à proximité
En pensant aux relations, tout le monde peut apporter beaucoup à la science. Être curieux suffit. Par exemple, on peut se demander pourquoi la classification des nombres fractionnaires est juste telle? Et trouvez la réponse dans une expérience de pensée pour mesurer le rapport des mêmes segments. Premièrement, les segments sont corrélés de 1 à 2. Ce rapport est compréhensible, il nous donne le nombre 2, qui montre combien de fois le segment le plus grand dépasse le plus petit. Et maintenant, allongons un segment légèrement plus petit. Que va-t-il se passer? Le rapport cessera d'être entier. L'excès obtenu de l'allongement nous empêche d'obtenir une réponse simple au problème. Mais nous pouvons l'utiliser comme règle. S'il correspond à un nombre entier de fois dans un demi-segment plus grand, alors nous pouvons exprimer le rapport à travers cet entier. Nous obtenons donc le rapport:
où N est le nombre de fois qu'il faut pour ajuster l'excédent d'étirement de la plus petite longueur à la moitié de la plus grande longueur. Nous avons donc obtenu un nombre rationnel. Il est toujours donné par le rapport des entiers. Si nous étendons maintenant le segment plus petit un peu plus longtemps, nous pouvons obtenir une situation où, peu importe combien nous multiplions le segment plus petit par un certain entier, nous ne pouvons pas obtenir une correspondance exacte avec un certain nombre de longueurs du segment plus grand. Nous avons donc obtenu un nombre irrationnel qui caractérise le nouveau rapport. Notez qu'un décalage microscopique de la frontière du segment conduit à un processus sans fin d'identification du rapport des longueurs. Une étape pour l'humble chercheur et un énorme changement pour la théorie des nombres - un nouvel élément dans la classification est nécessaire. Une étape et - de la micro-taille à l'infini. D'une catégorie de numéros à une toute nouvelle, fondamentalement incompatible avec la précédente. N'est-ce pas une star?
Mais en fait, nous avons légèrement changé un segment. D'où vient donc cette catégorie fondamentalement nouvelle? En général, la classification est importante pour sa capacité à correspondre exactement à la réalité. Mais quel genre de précision est venu avec des nombres irrationnels? Ils vous permettent de modéliser n'importe quel rapport, et pas seulement le rapport des entiers, il est donc vraiment judicieux de séparer ces classes. Mais ce n'est pas tout exact, parce que je veux comprendre toutes ces infinités, comment elles apparaissent, ce qu'elles signifient et pourquoi elles existent. Certes, à l'infini, tout n'est pas facile, mais parce que pour l'instant nous allons traiter de relations finies. Il semble que tout soit simple avec eux, prenez N, divisez-le par M et obtenez un nombre fractionnaire. Ce sera très bien si le nombre s'avère court, par exemple 2,5 ou 3,25. Mais le plus souvent au monde sont des relations de la forme 4.12 (3456), c'est-à-dire encore avec des infinis, mais ce sont des infinis «en période». En remarquant simplement les nombres répétés, vous pouvez très facilement et de manière compacte enregistrer un nombre à partir d'un nombre infini de caractères. Voilà comment nous avons fait face à l'infini. Aussi un petit astérisque. Mais ce n'est qu'un coup d'œil rapide.
Allons maintenant à la curiosité et posons des questions. Et pourquoi certains nombres fractionnaires sont-ils finis et d'autres infinis? Et pourquoi certains types d'infinis sont-ils infiniment longs, tandis que d'autres ont une période? Et pourquoi avant la période du numéro 4.12 (3456), nous voyons les chiffres 1 et 2? Et pourquoi existe-t-il une pré-période? Et pourquoi dans la période voyons-nous les chiffres 3 et 4? Et pourquoi la durée de la période dans cet exemple est-elle égale à quatre? Et pourquoi le nombre de nombres avant la période est-il égal à deux? Et nous n'avons jeté qu'un regard curieux sur un seul nombre fractionnaire. Et pour d'autres chiffres, les questions seront encore plus intéressantes.
Essayons de répondre. Pourquoi les nombres fractionnaires sont-ils finis? Très simple - en fait, c'est une "illusion d'optique". Plus précisément - nous avons utilisé une astuce. Par exemple, pour obtenir le nombre 2,5, vous pouvez diviser 5 par 2. Et pour cela, nous avons tous appris à l'école la méthode de diviser le "coin". Mais regardons de plus près cette méthode. Et puis nous constatons que le fakir agit comme suit - il multiplie le dividende par une constante contenant le diviseur, ou ses facteurs. Et puis il réduit exactement les facteurs de la constante aux facteurs du diviseur. Cela ressemble à ceci:

Voilà tous les miracles - un diable d'un diviseur est réduit à un diable d'une constante

ce qui est égal à

, et un cinq est resté en conséquence, qui est écrit après le séparateur décimal. Le nombre est
jamais partagé
, il multiplie par

du montant

. Mais nous ne le voyons pas, grâce à la très "illusion d'optique" que nous avons formée à l'école pour créer de manière indépendante lors de chaque opération de division. Eh bien, n'est-ce pas une star? Il ne restait plus qu'à pousser le feuillage sur les représentations sourdes du temps de l'école primaire, quand on voyait la lumière de quelque chose de nouveau, pas tout à fait ordinaire, qui n'est pas enseigné à l'école (mais en vain).
Expliquons maintenant «l'illusion d'optique» à un niveau légèrement supérieur. Nous avons simplement traduit le résultat de la division dans un format pratique pour le stockage et la perception. Le nombre lui-même ne dépend pas du format. Et le nombre de caractères qu'il contient est également. Nous avons déjà vu la possibilité de placer des crochets autour d'une période, et ainsi de réduire l'infini à la longueur de la période et de deux crochets. Et c'est aussi un format de données, mais utilisé pour les fractions périodiques. Et le format des fractions finies masque l'infini en réduisant par des facteurs la base du système de nombres décimaux. Si nous prenons, par exemple, le système numérique ternaire, alors la division de 5 par 2 ressemblera à ceci:

Autrement dit, nous avons obtenu l'infini sous la forme d'une fraction périodique, car maintenant nous avons utilisé une autre constante qui ne contient pas de facteurs qui peuvent être réduits avec le nombre 2. Mais dans un système hexadécimal, le résultat deviendrait à nouveau final - 2,3. Mais le nombre lui-même reste quelque part dans l'ombre, et le meilleur record serait probablement 5/2, et tout le reste est la question du choix du format de présentation pour ce nombre.
Maintenant sur des fractions infinies. Les périodiques sont obtenus en divisant les entiers, et les irrationnels (avec une longueur de période infinie) sont obtenus en calculant une racine d'un certain degré à partir d'un entier. C'est-à-dire que les gens ont dérivé deux catégories de division de l'abstraction des nombres entiers - avec différents facteurs et avec les mêmes. La première option vous permet de diviser n'importe quel entier en n'importe quel autre entier, mais parfois elle donne un résultat fractionnaire. La deuxième option vous permet de diviser les nombres uniquement en ceux qui sont exactement égaux au résultat de la division (y compris multiple pour les racines de grands degrés). En général, nous avons la même division, mais sans limitation sur le résultat et avec la restriction. La restriction nous amène à deux options: soit réduire le diviseur avec un facteur du dividende (et vous pouvez alors obtenir un entier égal au diviseur), soit diviser le dividende irréductible par un certain nombre. Quel peut donc être un "certain nombre"? S'il s'agit d'un entier, alors nous obtenons une fraction (le dividende et le diviseur sont irréductibles), qui n'est pas égal à un entier. Par conséquent, comme les entiers ne correspondent pas, vous devez rechercher une fraction qui serait égale au résultat. Les fractions finies disparaissent également, car elles représentent en fait un certain nombre de la forme
qui, multiplié par lui-même, nous donnerait une nouvelle fraction de la forme
, ce qui nous donne encore une fraction finie ou périodique, et non un entier. Par conséquent, il est nécessaire de sélectionner une fraction qui réduirait le rapport de leurs carrés à un entier avec une croissance infinie de N et M. Pourquoi pour des nombres infinis le rapport
peut être rendu entier, mais pas pour la fin? Parce que plus il y a de nombres, moins leur influence sur le résultat est discrète. L'entier qui suit l'un quelconque choisi est nécessairement différent de celui-ci par un. Et cette unité ne vous permet pas de définir précisément le résultat souhaité, car, par exemple, entre 1/1000 et 2/1000, il y a une infinité de nombres, par exemple 11/10000 ou 145/100000, etc. Par conséquent, en augmentant la longueur du nombre, il est possible à l'infini d'obtenir n'importe quel résultat avec une précision quelconque. Et puis multipliez-le par lui-même et obtenez un entier.
Et en même temps, la période d'une telle fraction devient vraiment infinie, comme nous le verrons plus loin. Et une période infinie est la propriété d'un nombre irrationnel, auquel nous sommes passés de nombres tout à fait rationnels. Voici une telle lumière stellaire qui se transforme en douceur dans l'obscurité de l'infini.Mais pourquoi avons-nous besoin de cette jonction entre deux classes de nombres? Peut-être qu'un seul suffit? Essayons de simuler. Nous avons donc obtenu exactement la racine d'un entier, nous avons trouvé deux grands entiers tendant vers l'infini, qui, lorsqu'ils sont au carré et divisés l'un par l'autre, donnent un entier. Ajoutez maintenant un à l'un de ces nombres infiniment grands. Que se passera-t-il alors? Dans notre langage habituel, nous avons obtenu une définition pour un nouveau nombre, qui n'est pas périodique (car il a une période infinie) et en même temps n'est pas la racine de l'ensemble. Autrement dit, le nouveau nombre ne rentre pas dans la classification qui nous est donnée à partir des nombres rationnels et irrationnels. Et maintenant, tous ces numéros ont été appelés par des mathématiciens transcendantaux, parce que vous devez les mettre quelque part. Mais un point intéressant - au début, il y avait des racines d'entiers, appelés nombres irrationnels,puis «d'autres» nombres sont apparus. C'est-à-dire, premièrement, dans l'intérêt de la tradition grecque ancienne, la surestimation de l'importance des nombres entiers a tous été classés précisément sur la base des méthodes d'obtention à partir des nombres entiers. La première méthode était la division et les nombres rationnels qui en découlaient. Ensuite, les gens ont rencontré des racines. Il y avait donc des chiffres irrationnels. Et en plus du rationnel et de l'irrationnel, une troisième catégorie est apparue. De plus, la troisième catégorie était d'abord une terrible rareté qu'Euler a découverte, mais à part la découverte d'Euler, il n'y en avait tout simplement pas d'autres. Et il a été décidé de diviser l'irrationnel en deux classes - algébrique (c'est-à-dire croissant à partir des racines) et transcendantal (spécial, exceptionnel, allant au-delà, car seul Euler pouvait les trouver). Mais plus tard, les nombres qui ne provenaient pas des racines sont devenus massifs, et les mathématiciens ont même déterminé qu'il y en avait beaucoup plus,que algébrique. Par conséquent, la transcendance (caractéristique) de ces nombres n'est devenue qu'un hommage à la tradition. Bien que si nous rappelons le concept de corrélation, tous ceux rationnels, irrationnels, algébriques et transcendantaux deviennent immédiatement des noms artificiels pour une division très conditionnelle des nombres résultant d'un simple déplacement de la fin de l'un des segments comparés. Eh bien, avec une telle approche, les nombres transcendantaux deviennent simplement «le reste», c'est-à-dire que si, à partir de la relation des segments, pour maintenir la tradition d'extraction des nombres entiers, nous sélectionnons les classes obtenues par les opérations de division et d'extraction de la racine à partir de nombres entiers, nous obtenons seulement rationnel et algébrique, mais tous le reste est transcendantal. Autrement dit, au total, il n'y a que trois catégories de fractions infinies. Par conséquent, le nom "transcendantal" devient quelque peu tendu,tu ne trouves pas? Eh bien, d'accord, parce que la tradition est notre tout, même dans une science aussi exacte que les mathématiques.C'est tout pour l'instant. Dans la prochaine série, parlons d'étoiles rationnelles.