Comment colorer correctement les polynômes

Les polynômes ne sont pas seulement des exercices en matière abstraite. Ils sont parfaits pour détecter des structures dans des endroits inattendus.

En 2015, ancien poète devenu mathématicien, Jun Ho a aidé à résoudre le problème formulé il y a environ 50 ans. Il était associé à des objets mathématiques complexes, des " matroïdes " et des graphiques (combinaisons de points et de segments). Et il était également lié à des polynômes - expressions que nous connaissons des leçons de mathématiques, consistant en la somme de variables élevées à divers degrés.

À un certain moment à l'école, vous avez probablement traversé l'ouverture des parenthèses dans les polynômes. Par exemple, vous vous souvenez peut-être que x ² + 2xy + y ² = (x + y) ² . Une astuce algébrique pratique, mais où peut-elle être utile? Il s'avère que les polynômes aident parfaitement à révéler les structures cachées - et Ho a activement utilisé ce fait dans sa preuve. Voici une énigme simple illustrant cela.

Supposons que nous devions asseoir deux équipes de joueurs sur une table carrée. Pour éviter la fraude, vous devez vous assurer que les joueurs ne sont pas assis à côté des autres joueurs de leur équipe. Combien de méthodes d'assise existe-t-il?

Commençons par les sièges de l'équipe rouge et bleue. Disons que le joueur rouge se trouve en haut du tableau:



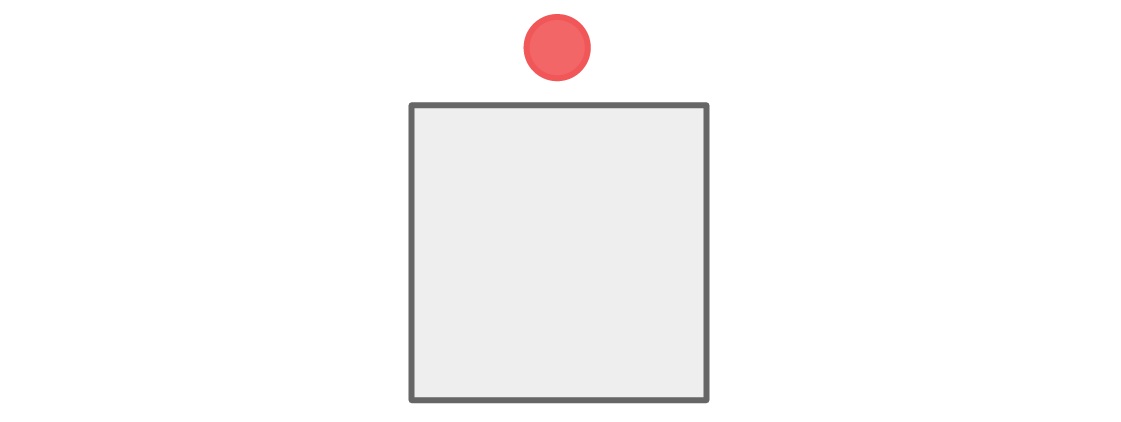
Il y a deux places près de la première place - droite et gauche - et pour satisfaire la règle, ces places doivent être occupées par des joueurs bleus.



L'espace ci-dessous est adjacent aux deux bleus, donc le joueur rouge doit s'y asseoir.



Aucun des joueurs n'est assis à côté d'un membre de leur équipe et notre condition est remplie.

On pourrait aussi commencer avec le joueur bleu en haut. Des considérations similaires conduisent à l'arrangement suivant:



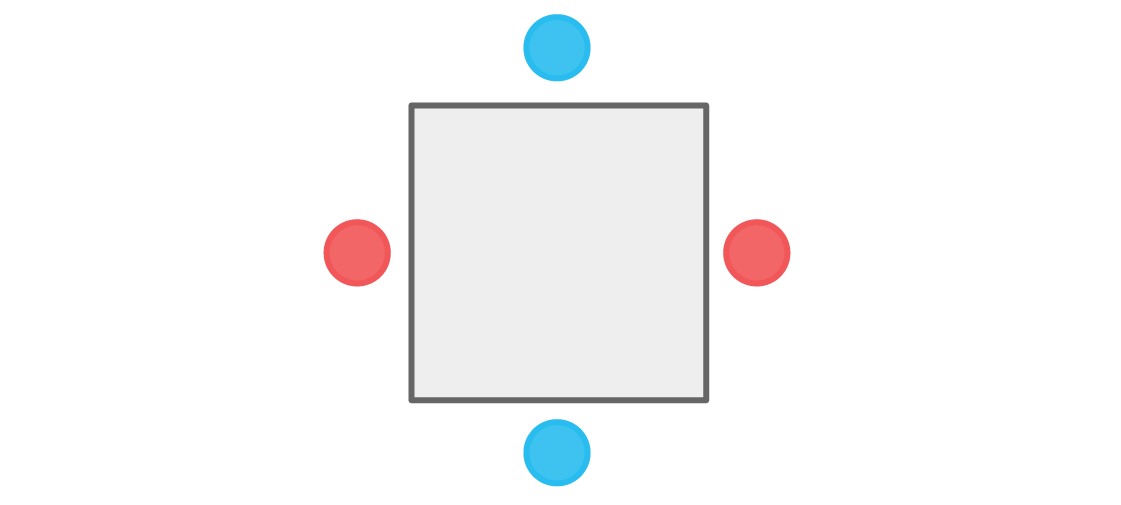
Encore une fois, aucun joueur ne s'assoit à côté des autres membres de son équipe. Notre condition est remplie et une telle disposition des sièges est acceptable. En fait, il en existe exactement deux. Dès que nous choisissons la couleur de la première place, tout le reste est entièrement défini.

Il existe un moyen de découvrir qu'il n'y a que deux configurations de sièges possibles sans dessiner tous ces diagrammes. Commençons par le haut: nous avons deux options, rouge et bleu. Après ce choix, il reste une option (une couleur différente) pour les sièges gauche et droit. Et pour le siège inférieur, il ne reste qu'une seule option - la couleur avec laquelle nous avons commencé. En utilisant le «principe fondamental du calcul», nous savons que le nombre total d'opportunités est le résultat de la multiplication du nombre d'opportunités pour chacune des options. Cela nous donne 2 × 1 × 1 × 1 = 2 plants, comme nous l'avons déterminé à partir de nos diagrammes.

Ajoutez maintenant la troisième commande avec la troisième couleur. Imaginez que nous ayons des joueurs rouges, bleus et jaunes. Combien d'agencements de sièges peuvent être réalisés, à condition que les places voisines soient de couleurs différentes? Pour l'image de toutes les possibilités, vous devrez dessiner tout un chariot de diagrammes, alors essayons plutôt de faire des calculs.

Pour la première place, nous avons maintenant un choix de trois couleurs. Après ce choix, nous pouvons choisir l'une des deux couleurs restantes pour les endroits gauche et droit.

Qu'est-ce qui sera en dessous du carré? Il y a une tentation de déclarer que pour le dernier siège, il n'y aura qu'une seule option, car il est à côté des sièges gauche et droit. Mais vous sentez-vous défectueux dans cette logique?



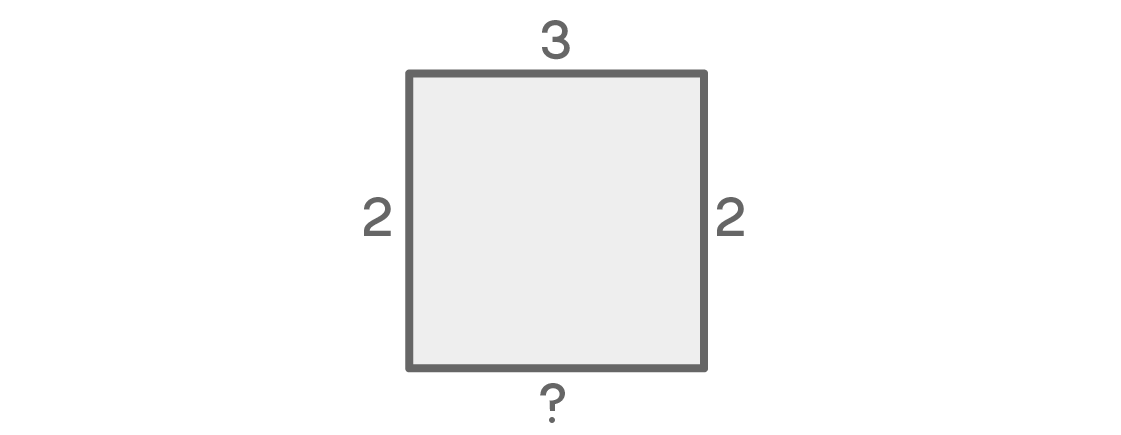
En effet, si les endroits gauche et droit ont des couleurs différentes, alors pour la place du bas il n'y aura qu'une seule option. Si à gauche, par exemple, il est bleu et à droite rouge, alors le bas doit être jaune. Mais que se passe-t-il si les couleurs gauche et droite sont les mêmes? Dans ce cas, pour la dernière place, vous aurez le choix entre deux options. Ce dernier choix dépend des précédents, ce qui complique nos calculs.

Nous devons considérer deux cas différents: quand les couleurs à gauche et à droite coïncident, et quand elles diffèrent.

Si les couleurs à gauche et à droite coïncident, le nombre de possibilités pour chacun des lieux ressemble à ceci:



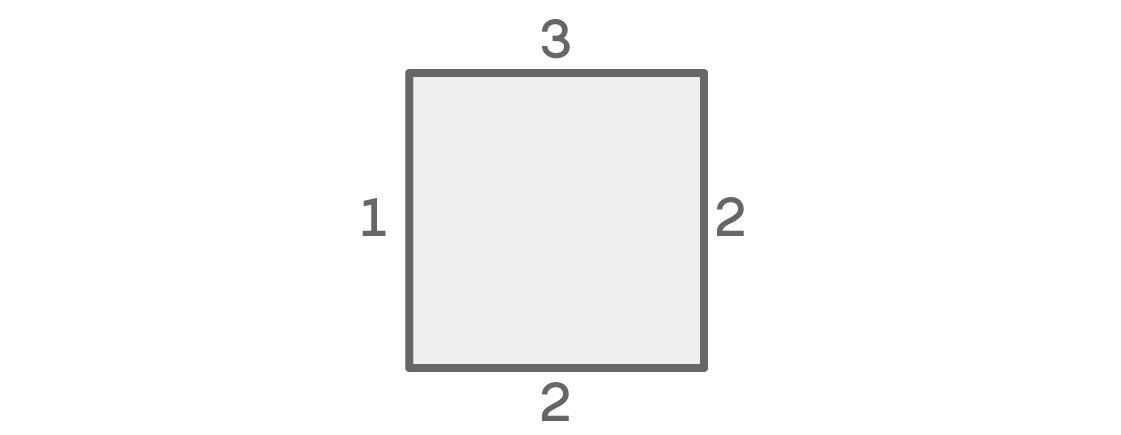
Pour le siège supérieur, nous avons trois options. Il en reste deux à droite. Puisque nous supposons que les endroits gauche et droit ont la même couleur, nous n'avons qu'une seule option pour l'endroit gauche: la même couleur que la droite. Enfin, comme la couleur est la même à gauche et à droite, nous pouvons choisir l'une des deux couleurs restantes pour le siège inférieur. En conséquence, nous obtenons 3 × 2 × 1 × 2 = 12 configurations de sièges possibles.

Examinons maintenant ces possibilités lorsque les couleurs à droite et à gauche sont différentes:



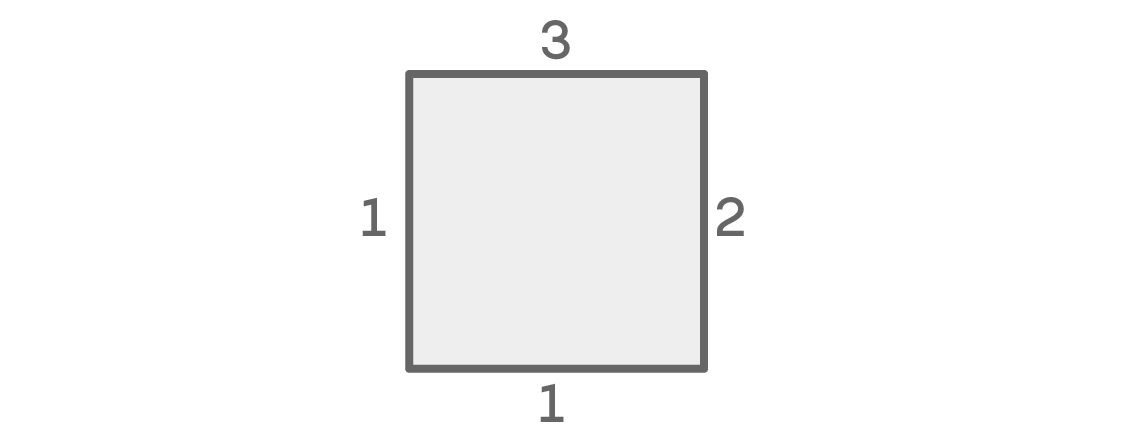
Nous avons encore trois options pour le haut et deux pour le bon endroit. La place de gauche a encore une option, mais pour une raison différente: elle ne peut pas être la même que la partie supérieure, voisine, et ne peut pas être la même que la droite, selon notre condition. Et, comme les couleurs à droite et à gauche sont différentes, il n'y a qu'une seule option à gauche pour la place du bas (la même que pour le haut). Ce cas donne 3 × 2 × 1 × 1 = 6 dispositions possibles.

Étant donné que ces deux options couvrent toutes les possibilités, nous les additionnons et obtenons 12 + 6 = 18 configurations de sièges possibles.

L'ajout d'une troisième couleur a compliqué notre tâche, mais notre travail acharné sera récompensé. Maintenant, nous pouvons utiliser cette stratégie pour 4, 5 ou n'importe quel nombre q de couleurs différentes.

Quel que soit le nombre de couleurs, nous aurons toujours deux étuis: gauche et droite seront de la même couleur ou de couleurs différentes. Supposons que nous ayons un choix de q couleurs. Voici un tableau montrant le nombre d'options pour chaque côté, dans le cas où les couleurs droite et gauche sont les mêmes:



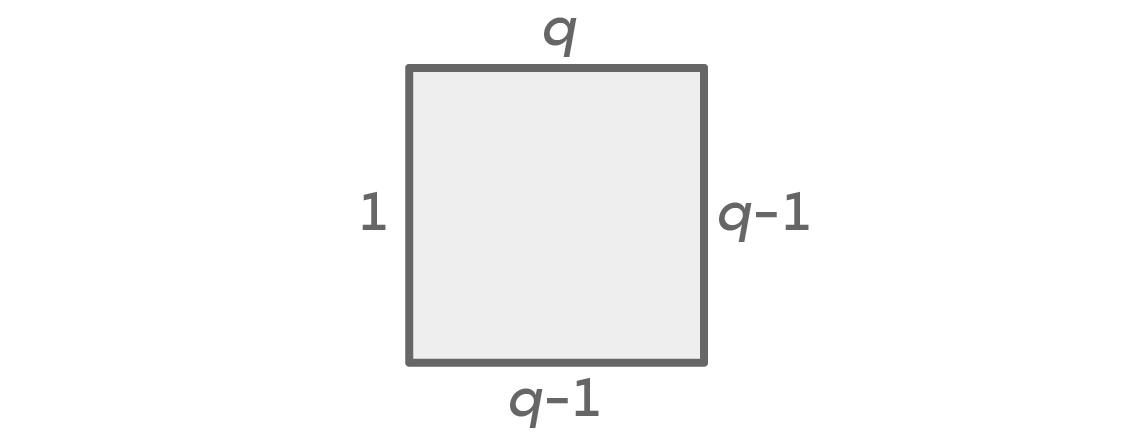
Nous avons d'abord q couleurs pour le siège supérieur, et q-1 pour la droite. Puisque nous avons supposé que les couleurs à gauche et à droite sont les mêmes, nous n'avons qu'une seule option pour la couleur de gauche. Cela laisse des options q-1 pour le point inférieur, car il peut s'agir de n'importe quelle couleur autre que celle que nous avons choisie pour les points gauche et droit. Le principe fondamental du calcul nous donne q × (q - 1) × 1 × (q - 1) = q (q - 1) ² configurations possibles.

Si les endroits gauche et droit sont colorés différemment, alors nous pouvons calculer les possibilités comme ceci:



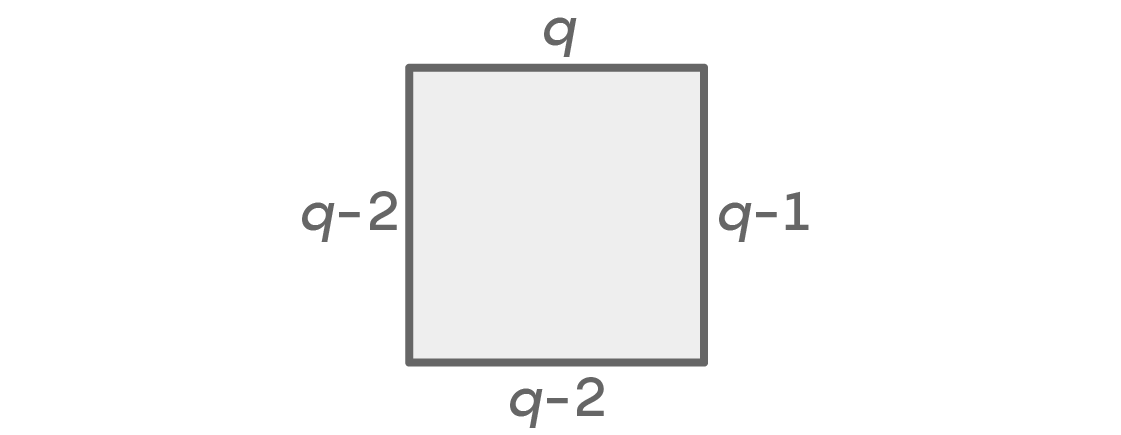
Encore une fois, nous avons q options pour le haut et q-1 pour les bons endroits. Il ne peut pas y avoir la même couleur à gauche qui est sélectionnée pour les endroits en haut et à droite, il y a donc des options q-2. Il peut y avoir n'importe quelle couleur ci-dessous, à l'exception des deux que nous avons utilisées à gauche et à droite, ce qui donne à nouveau des options q-2. On obtient la somme q × (q - 1) × (q - 2) × (q - 2) = q (q - 1) (q - 2) ² agencements de sièges possibles. Étant donné que ces deux situations couvrent toutes les options, nous, comme précédemment, les additionnons et obtenons le nombre total d'arrangements possibles: q (q - 1) ² + q (q - 1) (q - 2) ² .

Une telle expression peut sembler une réponse étrange à la question: "Combien de sièges différents pour différentes équipes à la table carrée, de sorte que deux membres d'une même équipe ne s'assoient pas côte à côte?" Cependant, ce polynôme contient beaucoup d'informations sur notre problème. Il nous donne non seulement une réponse quantitative, mais révèle également la structure de notre tâche.

Un tel polynôme est appelé « polynôme chromatique » car il répond à la question: combien de méthodes existent pour colorer les sommets d'un réseau (ou graphe) de telle sorte que toute paire de sommets voisins ait des couleurs différentes?

Initialement, notre problème était lié aux sièges autour de la table, mais nous pouvons facilement le transformer en une question sur la coloration des sommets du graphique. Au lieu de personnes à table:



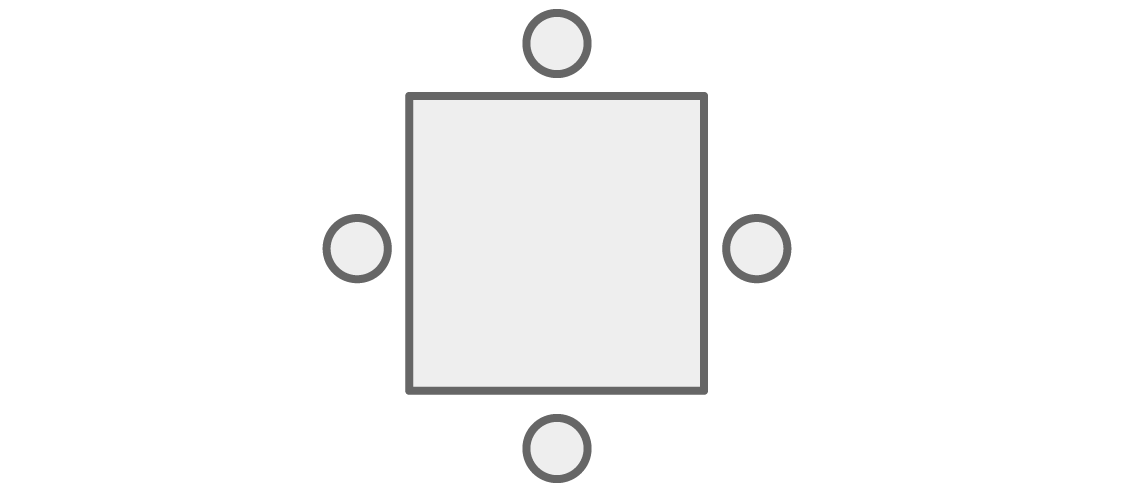
nous les imaginerons sous forme de pics reliés par des bords dans le cas où ils seront assis à côté de:



Maintenant, toute coloration des sommets du graphique peut être représentée comme le siège de personnes autour du carré, où «s'asseoir à côté de» à la table signifie «avoir un bord commun» sur le graphique.

Maintenant, après avoir reformulé notre problème sous forme de graphe, nous revenons au polynôme chromatique. Nous l'appelons P (q).

P (q) = q (q - 1) ² + q (q - 1) (q - 2) ²

Une propriété remarquable de ce polynôme est qu'il répond à la question de la coloration pour tout nombre de couleurs possible. Par exemple, pour répondre à une question avec trois couleurs, nous mettons q = 3, et nous obtenons:

P (3) = 3 (3 - 1) ² + 3 (3 - 1) (3 - 2) ² = 3 × 2 ² + 3 × 2 × 1 ² = 12 + 6 = 18

C'est la réponse que nous avons reçue dans le cas de trois équipes. Et si on met q = 2:

P (2) = 2 (2 - 1) ² + 2 (2 - 1) (2 - 2) ² = 2 × 1 ² + 2 × 1 × 0 ² = 2 + 0 = 2

Cela vous semble familier? C'est la réponse à notre première énigme, avec deux équipes. Nous pouvons trouver des réponses pour quatre, cinq ou même 10 équipes différentes, en substituant simplement la valeur souhaitée à q: P (4) = 84, P (5) = 260 et P (10) = 6 570. Le polynôme chromatique a pris une structure fondamentale du problème en résumant notre stratégie de comptage.

Nous pouvons révéler plus de détails sur la structure en effectuant des opérations algébriques sur notre polynôme P (q) = q (q - 1) ² + q (q - 1) (q - 2) ² :

= q (q - 1) (q - 1) + q (q - 1) (q - 2) ²
= q (q - 1) ((q - 1) + (q - 2) ² )
= q (q - 1) (q - 1 + q ² −4q + 4)
= q (q - 1) (q ² −3q + 3)

Nous avons extrait le facteur q (q - 1) de chaque partie de la somme et combiné des termes similaires, réduisant le polynôme à une forme factorisée. Et sous cette forme, le polynôme peut nous parler de la structure à l'aide de ses «racines».

Les racines d'un polynôme sont des valeurs d'entrée auxquelles il devient égal à zéro en sortie. Il est plus facile de trouver les racines sous la forme factorisée: étant donné que le polynôme est exprimé en parties multipliées, toute valeur à laquelle l'un des facteurs est égal à zéro réinitialise l'ensemble du produit.

Par exemple, notre polynôme P (q) = q (q - 1) (q ² - 3q + 3) a un facteur (q - 1). Si nous prenons q = 1, ce facteur devient égal à zéro, comme tout le résultat de la multiplication. Autrement dit, P (1) = 1 (1 - 1) (1 ² - 3 × 1 + 3) = 1 × 0 × 1 = 0. De même, P (0) = 0 × (–1) × 3 = 0 Par conséquent, q = 1 et q = 0 sont les racines de notre polynôme. (Vous pouvez être intéressé par le facteur (q ² - 3q + 3). Comme il n'est égal à zéro pour aucun q réel, il ne donne pas de nouvelles racines à notre polynôme chromatique).

Ces racines ont un sens dans le cadre de notre graphique. Si nous avons le choix de la même couleur, chaque sommet doit être de la même couleur. Il n'est pas possible de colorer le graphique de sorte que tous les sommets adjacents aient des couleurs différentes. C'est précisément ce qui signifie que q = 1 est la racine de notre polynôme chromatique. Si P (1) = 0, alors il y a exactement zéro façon de colorer le graphique de sorte que les sommets voisins ne soient pas les mêmes couleurs. Il en va de même pour la version avec un nombre de couleurs nul, P (0) = 0. Les racines de notre polynôme chromatique nous renseignent sur la structure de notre graphe.

La capacité de voir la structure à travers l'algèbre devient encore plus évidente si nous considérons d'autres graphiques. Regardons un graphique triangulaire:



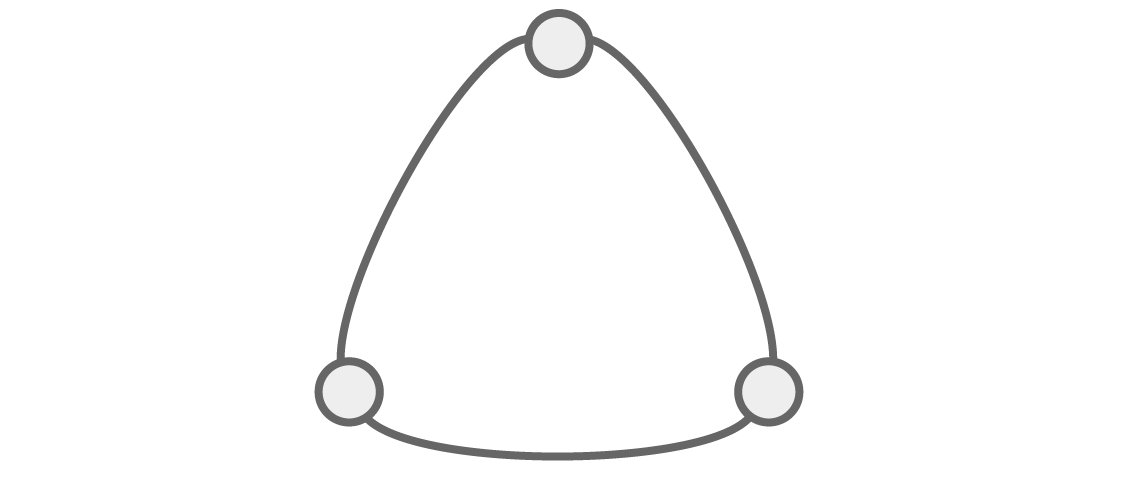
Combien de façons existe-t-il de colorer ce graphe q avec des couleurs pour que les sommets voisins ne soient pas les mêmes couleurs?

Comme d'habitude, pour les deux premiers sommets voisins, il existe des options q et q-1. Et puisque le dernier sommet est adjacent aux deux premiers, il devrait différer en couleur des deux, ce qui nous laisse des options q-2. Cela nous donne le polynôme chromatique pour ce graphe triangulaire: P (q) = q (q - 1) (q - 2).

Dans cette forme de factorisation, ce polynôme chromatique nous dit quelque chose d'intéressant: il a une racine q = 2. Et si P (2) = 0, il devrait être impossible de colorier ce graphe avec deux couleurs pour qu'il n'ait pas deux sommets adjacents de même couleur. En est-il ainsi?

Imaginez que nous marchons en cercle dans ce triangle, colorant les pics le long du chemin. Si nous n'avons que deux couleurs, nous devons les alterner après chaque sommet: si le premier est rouge, alors le second sera bleu, ce qui signifie que le troisième devrait à nouveau être rouge. Mais les premier et troisième pics sont adjacents et ne peuvent pas être rouges tous les deux. Deux couleurs ne suffisent pas, comme le prédit le polynôme.

En utilisant un argument alternatif similaire, nous pouvons arriver à une généralisation significative: le polynôme chromatique de toute boucle fermée avec un nombre impair de sommets doit avoir une racine égale à 2. Puisque si vous alternez deux couleurs et vous déplacez le long d'une boucle de longueur impaire, les premier et dernier sommets colorés seront de la même couleur . Mais tout comme il s'agit d'une boucle, ils seront adjacents. La coloration n'est pas possible.

Par exemple, nous pouvons utiliser diverses techniques pour déterminer que pour une boucle à cinq sommets, le polynôme chromatique ressemble à ceci: P (q) = q ⁵ - 5q ⁴ + 10q ³ - 10q ² + 4q. En tenant compte de cela, nous obtenons P (q) = q (q - 1) (q - 2) (q2 - 2q + 2). Comme prévu, il s'avère que q = 2 est la racine et P (2) = 0. Fait intéressant, dès que nous trouvons cette connexion entre les graphiques et leurs polynômes, les idées commencent à fonctionner dans les deux sens. Les polynômes peuvent nous fournir des informations sur la structure des graphiques et les graphiques peuvent nous renseigner sur la structure des polynômes.

C'est la recherche de structure qui a conduit June Ho à prouver l'hypothèse de 40 ans de Reed concernant les polynômes chromatiques. L'hypothèse stipule que si nous énumérons les coefficients du polynôme chromatique dans l'ordre, en ignorant leurs signes, la condition suivante sera remplie: le carré de tout coefficient doit être au moins le produit de deux voisins. Par exemple, dans le polynôme chromatique de notre boucle à cinq sommets, P (q) = q ⁵ - 5q ⁴ + 10q ³ - 10q ² + 4q, nous voyons que 5 ² ≥ 1 × 10, 10 ² ≥ 5 × 10 et 10 ² ≥ 10 × 4. Il en résulte, par exemple, que tous les polynômes ne peuvent pas être chromatiques: les polynômes chromatiques associés aux graphiques ont une structure plus profonde. De plus, la connexion entre ces polynômes et d'autres domaines a permis à Ho et ses co-auteurs de répondre à une question beaucoup plus large liée à l'hypothèse Roth, plusieurs années après la preuve de l'hypothèse Reed.

Peut-être que les polynômes sont mieux connus pour leur pire forme - comme des exercices abstraits dans la manipulation formelle des expressions algébriques. Mais les polynômes et leurs propriétés - racines, coefficients, formes diverses - aident à révéler des structures dans des endroits inattendus, créant des liens avec l'algèbre dans tout ce qui nous entoure.

Exercices

1. Un graphe complet est un graphe dont chaque paire de sommets est reliée par une arête. Trouvez le polynôme chromatique d'un graphe complet de cinq sommets.


2. Trouvez le polynôme chromatique pour le graphique suivant (utilisez les informations sur les polynômes chromatiques des graphiques plus simples).




3. Un graphique est appelé recto-verso si ses sommets peuvent être divisés en deux groupes, A et B, de sorte que les sommets de A ne sont adjacents qu'aux sommets B et que les sommets B ne sont adjacents qu'aux sommets de A. Supposons que le graphe G ait un polynôme chromatique P (q). Quelle propriété P (q) vous permet de conclure que le graphe G est bilatéral?