Il existe de nombreux articles sur Internet avec une description de l'algorithme de descente de gradient. Il y en aura un autre.

Le 8 juillet 1958, le New York Times écrivait : «Un psychologue montre un embryon d'ordinateur conçu pour lire et devenir plus sage. Développé par la Marine ... l'ordinateur de 704 $, qui a coûté 2 millions de dollars, a appris à distinguer entre gauche et droite après cinquante tentatives ... Selon la Marine, ils utilisent ce principe pour construire la première machine à penser de la classe Perceptron, qui peut lire et écrire; le développement devrait être achevé dans un an, pour un coût total de 100000 $ ... Les scientifiques prédisent que les Perceptrons pourront plus tard reconnaître les gens et les appeler par leur nom, traduisant instantanément les discours oraux et écrits d'une langue à l'autre. M. Rosenblatt a déclaré qu'en principe, il est possible de construire des «cerveaux» qui peuvent se reproduire sur la chaîne de montage et qui seront conscients de leur propre existence »(cité et traduit du livre de S. Nikolenko,« Deep learning, immersion dans le monde des réseaux de neurones »).

Ah, ces journalistes savent intriguer. Il est très intéressant de comprendre ce qu'est vraiment une machine à penser de la classe Perceptron.

Classification binaire (binaire) des objets, neurone artificiel de la classe Perceptron

Voici notre neurone artificiel, il divise les objets en deux classes (effectue une classification binaire des objets):

Nous avons donc:

• Entrée: objet d'échantillonnage - vecteur d'espace à m dimensions $$$x = (x_1, ..., x_m)$
• Poids $$$w = (w_1, ..., w_m)$ un pour chaque caractéristique de l'objet échantillon (également un vecteur à m dimensions)
• À l'intérieur: additionneur $$$SUM = w_1x_1 + ... + w_mx_m = \ sum _ {j = 1} ^ {m} w_ {j} x_ {j}$ - somme pondérée des entrées de neurones
• Suivant: activation $$$Φ (x, w) = Φ (SUM)$
• Plus loin encore: quantificateur (seuil) - θ [thêta]
• Activation + seuil - prédiction de l'étiquette de classe d'un objet basée sur la somme pondérée des entrées de neurones (attributs d'objet). Cette partie définit l'architecture spécifique du neurone.
• Sortie: étiquette de classe d'objet (l'une des deux) $$$\ hat {y} = \ {1, -1 \}$

Classification - parce qu'un neurone assigne une classe à un objet, binaire ( binaire ) - car il n'y a que deux classes possibles.

$$$\ chapeau {y}$ [jeu avec un couvercle] - nous indiquerons la valeur de classe prédite (calculée) pour l'objet $$$x$
$$$y$ [jeu normal sans couvercle] - vraies valeurs de classe (connues) pour un objet $$$x$ de l'ensemble de formation.

Les valeurs $$$x$ (ci-après $$$x$ et $$$w$ - ce ne sont pas des valeurs unitaires, mais des vecteurs) varient d'un objet à l'autre, les coefficients de pondération $$$w$ (une fois sélectionné) restent inchangés. Pour l'ensemble de formation pour chaque objet $$$x$ étiquette de classe connue $$$y$ . Au stade de la formation, vous devez choisir des poids $$$w$ de sorte que le modèle produit la valeur correcte $$$\ chapeau {y}$ (coïncidant avec $$$y$ ) pour le nombre maximum d'objets dans l'ensemble d'apprentissage. L'hypothèse de l'utilité d'un neurone ainsi formé repose sur l'espoir qu'il produira la valeur correcte avec les coefficients sélectionnés $$$\ chapeau {y}$ pour de nouveaux objets $$$x$ vraie valeur de classe $$$y$ pour lequel il n'est pas connu à l'avance.

La signification intuitive de la somme pondérée des entrées d'un neurone est que toutes les caractéristiques de l'objet (chacun des signes est l'une des entrées du neurone) affectent le résultat de la classification de l'objet, mais tous les signes ne sont pas également affectés. Dans quelle mesure - déterminer le poids; la remise à zéro d'un certain coefficient de pondération annule la contribution de l'attribut correspondant au montant total, c'est-à-dire cela revient à supprimer la fonction de l'objet.

Neurone linéaire adaptatif ADALINE

Le neurone ADALINE (neurone adaptatif linéaire) est un neurone artificiel ordinaire avec cette fonction d'activation:

$$ $$Φ (x, w) = Φ (SUM) = SUM$$

$$ $$\ Phi (x ^ {(i)}, w) = \ Phi (\ sum _ {j = 1} ^ {m} w_ {j} x_ {j} ^ {(i)}) = \ sum _ { j = 1} ^ {m} w_ {j} x_ {j} ^ {(i)}$$

Ci-après en exposant $$$i$ entre parenthèses désignera $$$i$ élément de l'ensemble de formation $$$x ^ {(i)}$ ou vraie valeur de classe $$$y ^ {(i)}$ ou valeur de classe prévue $$$\ hat {y} ^ {(i)}$ pour lui.

On peut dire qu'un tel neurone n'a tout simplement pas de fonction d'activation et que la valeur de la somme pondérée des entrées est envoyée à l'entrée du quantificateur (seuil). Mais pour l'uniformité, il sera plus commode de considérer que la valeur de la somme pondérée est prise comme activation.

Seuil (quantificateur) - prédit une étiquette de classe:

$$ $$\ hat {y} ^ {(i)} = \ left \ {\ begin {matrix} 1, \ Phi (x ^ {(i)}, w) \ ge \ theta \\ - 1, \ Phi (x ^ {(i)}, w) <\ theta \ end {matrix} \ droite.$$

Si la valeur d'activation est supérieure à une valeur seuil θ [thêta], alors le quantificateur attribue l'étiquette "1" à l'objet; si la valeur d'activation est inférieure au seuil θ, l'objet reçoit l'étiquette "-1".

Ici, nous pouvons formuler le problème en première approximation : nous devons sélectionner les paramètres du neurone

• facteurs de pondération $$$w_j, j = 1, .., m$
• et seuil θ [thêta]

de sorte que les valeurs de classe $$$\ chapeau y$ , que le neurone attribue aux objets de l'échantillon d'apprentissage, coïncidait avec les vraies valeurs des classes $$$y$ pour les mêmes éléments (ou, du moins, a donné le sens correct pour la majorité).

On transforme un peu la fonction de seuil, prenons le cas pour la classe $$$\ chapeau y = 1$ et transférer le seuil vers le côté gauche de l'inégalité:

$$ $$\ begin {réunis} \ Phi (x ^ {(i)}, w) \ ge \ theta \ hfill \\\ sum _ {j = 1} ^ {m} w_ {j} x_ {j} ^ {( i)} \ ge \ theta \ hfill \\ - \ theta + \ sum _ {j = 1} ^ {m} w_ {j} x_ {j} ^ {(i)} \ ge 0 \ hfill \\ \ end {réunis}$$

dénoter $$$w_ {0} = - \ theta$ et $$$x_ {0} = 1$

$$ $$\ begin {réunis} w_ {0} x_ {0} ^ {(i)} + \ sum _ {j = 1} ^ {m} w_ {j} x_ {j} ^ {(i)} \ ge 0 , w_ {0} = - \ theta, x_ {0} = 1 \ hfill \\\ sum _ {j = 0} ^ {m} w_ {j} x_ {j} ^ {(i)} \ ge 0, x_ {0} = 1 \ hfill \ end {réunis}$$

Comme nous le voyons, nous avons réussi à nous débarrasser d'un paramètre distinct θ, en l'introduisant sous le couvert d'un nouveau coefficient de poids $$$w_0$ sous le signe de la somme, tout en ajoutant à la description de l'objet un nouveau signe d'unité fictive $$$x_0 = 1$ .

Nous corrigerons la formulation du problème en tenant compte de la nouvelle notation.

Tâche ' : sélectionner les paramètres du neurone - facteurs de pondération $$$w_j, j = 0, .., m$ ,
$$$x_0 = 1$ (signe constant) - neurone fictif ( neurone à déplacement )

À partir de cet endroit, nous numérotons les signes et les poids c 0, pas 1. À propos du vecteur $$$w$ nous dirons qu'il s'agit de dimensions (m + 1) et non de dimensions m. Vecteur $$$x$ selon le contexte, on peut considérer (m + 1) -dimensionnel (pour la plupart dans les formules), mais rappelez-vous qu'en fait c'est m-dimensionnel.

Pourquoi un neurone ( dans notre cas, cependant, ce n'est pas un neurone, mais un signe d'un objet ou simplement une entrée, mais dans le cas d'un réseau multicouche, il se transforme en neurone et est généralement appelé de cette façon ) est fictif - c'est clair maintenant. Les raisons de son déplacement deviendront plus claires ultérieurement.

L'activation avec la somme ressemblera maintenant à ceci:

$$ $$\ Phi (x ^ {(i)}, w) = \ Phi (\ sum _ {j = 0} ^ {m} w_ {j} x_ {j} ^ {(i)}) = \ sum _ { j = 0} ^ {m} w_ {j} x_ {j} ^ {(i)}, x_ {0} ^ {(i)} = 1 \ forall i$$

Le seuil est désormais toujours 0 (zéro) (la valeur réelle est déplacée vers le paramètre $$$w_0$ ):

$$ $$\ hat {y} ^ {(i)} = \ left \ {\ begin {matrix} 1, \ Phi (x ^ {(i)}, w) \ ge 0 \\ - 1, \ Phi (x ^ {(i)}, w) <0 \ end {matrice} \ droite.$$

Encore une fois, nous formulons le problème en d'autres termes (la signification géométrique du problème)

Si nous regardons attentivement la formule de la fonction d'activation, nous verrons qu'il s'agit d'un hyperplan paramétrique dans (m + 1) -espace dimensionnel, tandis que dans les m premières dimensions, il coexiste avec les points des éléments de l'échantillon, et (m + 1) - La e-dimension est l'espace des valeurs de la fonction, séparé des éléments.

Maintenant, si nous assimilons la valeur d'activation à zéro (valeur de seuil), alors ce sera également un hyperplan, seulement déjà dans l'espace m-dimensionnel, c'est-à-dire complètement dans l'espace de valeur de l'élément $$$x$ . Cet hyperplan séparera les éléments. $$$x$ en deux groupes disjoints.

Habituellement, à cet endroit, ils disent que notre tâche consiste à sélectionner les valeurs des paramètres $$$w$ , c'est-à-dire construire un hyperplan m-dimensionnel dans l'espace des éléments de sorte que les éléments de l'ensemble d'apprentissage avec la vraie valeur de classe "1" soient d'un côté du plan, et les éléments avec la vraie classe "-1" de l'autre.

Pour ceux qui ne comprennent pas bien ce qui est écrit ici, lisez la suite - maintenant nous allons tous voir, c'est le premier. Deuxièmement, nous verrons également qu'un tel énoncé du problème, bien que valable, n'est pas entièrement complet.

Espace unidimensionnel (m = 1)

C'est là que le code commence à apparaître. Nous construisons tous les graphiques avec la bibliothèque Matplotlib habituelle, mais ici j'utilise également la bibliothèque Seaborn sur une ligne pour ajuster la zone du graphique, car J'aime la façon dont elle le fait, mais en principe, vous pouvez vous en passer.

# coding=utf-8 import matplotlib.pyplot as plt import seaborn as sns #      # (    -> ) sns.set(style='whitegrid', font_scale=1.8) #sns.set(style='whitegrid') #   ,   seaborn #plt.rcParams.update({'font.size': 16}) 

Nous prenons beaucoup de points à une dimension et y répondons:

 import numpy as np import math #  -  ( ) X1 = np.array([1, 2, 6, 8, 10]) #   ( ) y = np.array([-1, -1, 1, 1, 1]) 

Ici, nous avons chaque i-ème élément du tableau X1 - c'est le i-ème élément (i-ème point) de l'échantillon d'apprentissage (plus précisément, son 1er et seul attribut): $$$x ^ {(i)} = (X1 [i])$ , $$$x ^ {(i)} _ 1 = X1 [i]$

Chaque i-ème élément du tableau y est la bonne réponse, une vraie étiquette correspondant au i-ème élément de l'échantillon d'apprentissage avec un seul attribut X1 [i].

Nous prenons seulement 5 points, les deux premiers sont affectés à la classe "-1", les trois autres sont affectés à la classe "1".

Dessinez ces points sur la ligne:

 #  =0 plt.plot(X1, np.zeros(len(X1)), color='black', lw=2) #     =0 plt.scatter(X1[y==1], np.full(len(X1[y==1]), 0), color='blue', marker='o', s=300, label=u' x (1 ): -1 (y=1)') plt.scatter(X1[y==-1], np.full(len(X1[y==-1]), 0), color='red', marker='s', s=300, label=u' x (1 ): -2 (y=-1)') plt.xlabel(u'X1 ( )') plt.ylabel(u' ()') plt.legend(loc='upper left') plt.show() 

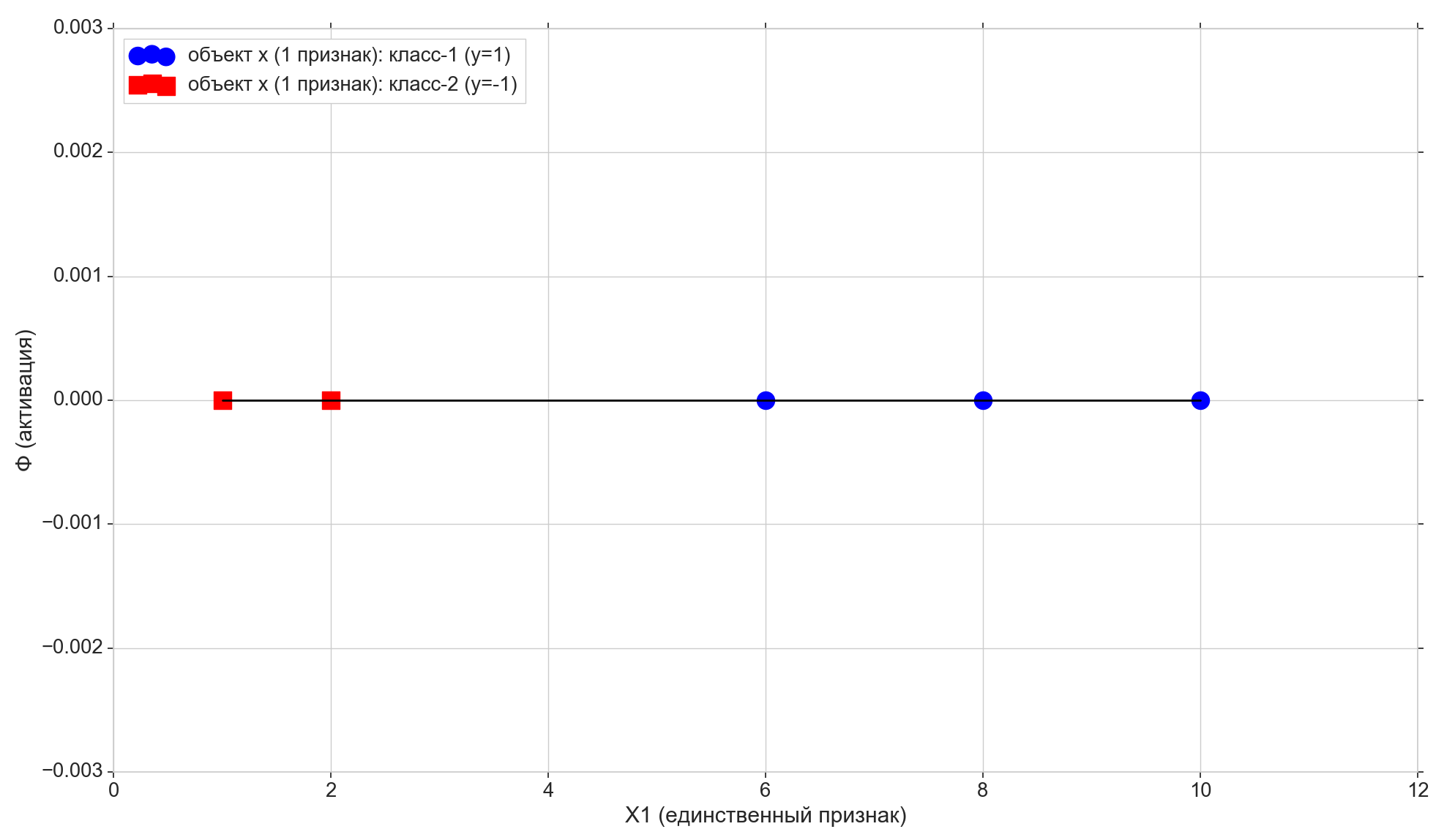
Voyons maintenant la fonction d'activation:

$$ $$\ Phi = w_ {0} + w_ {1} x_ {1}$$

Comme vous pouvez le voir, il s'agit d'une ligne paramétrique ordinaire sur le plan (dans un espace bidimensionnel, c'est-à-dire (m + 1)):

• sur l'axe horizontal on a les points des éléments (ce sont aussi les valeurs de l'attribut X1)
• sur la verticale - valeurs d'activation pour chaque élément
• paramètre $$$w_1$ - définit l'angle d'inclinaison,
• mais $$$w_0$ - se déplacer le long de l'axe vertical (voici la réponse au neurone de cisaillement ).

 w0 = -1.1 w1 = 0.4 #  y_ = w0 + w1*X1 #   (   -    ) plt.plot(X1, y_, color='violet', lw=3, label=u': w0=%0.2f, w1=%0.2f, sse/2=%0.2f'% (w0, w1, sse/2)) # :    =0 plt.scatter([-w0/w1], [0], color='violet', marker='o', s=300, label=u' ') #       plt.scatter(X1[y==1], y_[y==1], color='lightblue', marker='o', s=200, label=u': -1 (y=1)') plt.scatter(X1[y==-1], y_[y==-1], color='pink', marker='s', s=200, label=u': -2 (y=-1)') 

Rappelons également qu'après une petite conversion, notre seuil d'activation est devenu nul. Ainsi, si la projection du ième élément sur la ligne d'activation est inférieure à zéro, nous attribuons la classe -1 à l'élément ( $$$\ chapeau {y} = -1$ ), s'il est supérieur à zéro, on attribue la classe "1" ( $$$\ chapeau {y} = 1$ )

Point violet - intersection de la ligne d'activation avec l'axe $$$\ Phi = 0$ , séparant les éléments de différentes classes, c'est l'hyperplan très séparateur (pour l'espace à 1 dimension, le point est l'hyperplan) construit dans l'espace d'entité à 1 dimension (c'est-à-dire à m-dimension). Comme vous pouvez le voir, pour diviser les éléments en groupes, cela suffit, mais pour assigner des classes aux groupes, ce n'est plus suffisant. Afin d'assigner des classes aux éléments, nous avons besoin d'une activation directe (hyperplan bidimensionnel) construite dans l'espace 2-d (c'est-à-dire dans l'espace (m + 1) -d) «signes + activation»: la direction de la déviation d'activation par rapport à la verticale l'axe déterminera la classe des groupes d'éléments, car cela dépend si les projections des éléments sur l'activation sont supérieures ou inférieures à zéro.

Modification des paramètres $$$w_0$ et $$$w_1$ nous recevrons différentes lignes d'activation. Nous devons construire une telle ligne d'activation, c'est-à-dire trouver une telle combinaison de paramètres $$$w$ où la projection des deux premiers points de l'échantillon d'apprentissage sur la ligne d'activation est inférieure à zéro (pour eux, la valeur $$$\ chapeau {y} = y = -1$ ), et la projection des 3 points restants sera supérieure à zéro (pour eux $$$\ chapeau {y} = y = 1$ )

Il est bien évident que dans notre cas particulier, il n'y a rien de compliqué à construire une telle ligne, de plus, ces lignes peuvent généralement être construites en nombre infini. Mais nous essaierons de le construire de telle manière qu'un certain critère d'optimalité soit satisfait (cela peut affecter la qualité des prédictions futures), en plus il devrait y avoir la possibilité d'étendre l'algorithme au cas multidimensionnel.

Ici, nous notons également que nous avons spécifiquement sélectionné l'ensemble initial de points afin qu'il puisse être divisé par une telle ligne (pour 1-e: tous les éléments du premier groupe sont plus petits, tous les éléments du deuxième groupe sont plus grands qu'une certaine valeur fixe), c'est-à-dire de nombreux points d'entraînement sont séparables linéairement .

Ajoutez deux autres lignes horizontales au graphique correspondant aux classes {1, -1} et projetez les éléments dessus.

 #      (y=1, y=-1) plt.plot(X1, np.full(len(X1), 1), color='blue', label=u': -1 (y=1)') plt.plot(X1, np.full(len(X1), -1), color='red', label=u': -2 (y=-1)') #       (y=1, y=-1) plt.scatter(X1[y==1], np.full(len(X1[y==1]), 1), color='lightblue', marker='o', s=200, label=u' y: -1 (y=1)') plt.scatter(X1[y==-1], np.full(len(X1[y==-1]), -1), color='pink', marker='s', s=200, label=u' y: -2 (y=-1)') 

Points avec le projet de classe "-1" à la ligne de fond $$$\ Phi = -1$ , pointe avec le projet de classe "1" vers la ligne supérieure $$$\ Phi = 1$ .

Prenons attention à une dernière petite nuance. Nous traçons les valeurs d'activation le long de l'axe vertical, l'espace des valeurs d'activation est continu. Mais le résultat du classificateur (la fonction d'activation passée par le seuil) est un ensemble discret de deux éléments {-1, 1}, et non une échelle continue. Ici, nous prenons un ensemble discret de classes $$$y$ et le mettre sur une échelle d'activation continue $$$\ Phi$ de sorte que les valeurs de classe discrètes deviennent des points ordinaires sur l'échelle d'activation - des cas spéciaux de valeurs d'activation qu'il peut directement accepter ou approcher suffisamment près d'eux. À strictement parler, nous pourrions initialement prendre non pas les valeurs numériques comme des classes, mais les étiquettes de chaîne «classe-1» et «classe-2», auquel cas nous aurions à faire correspondre les étiquettes de chaîne aux valeurs numériques sur l'échelle d'activation. Par conséquent, dans notre cas, les valeurs des classes "-1" et "1" doivent être prises non pas comme des étiquettes de classe comme elles le sont, mais comme un mappage de classes marquées à l'échelle d'activation.

Il est temps d'entrer la métrique d'erreur

 #   -       #      plt.plot([X1, X1], [y_, y], color='orange', lw=3)#, label='err') 

Il est naturel d'accepter que plus la valeur d'activation pour l'élément sélectionné est proche de la valeur de classe pour le même élément, meilleure est la classe d'activation prédit pour cet élément. Ainsi, pour l'erreur de l'élément sélectionné, vous pouvez prendre la distance entre les points - la projection verticale de l'élément sur la ligne d'activation et la projection de l'élément sur la ligne horizontale de sa classe (vraie) connue. Sur le graphique: erreurs - lignes verticales orange.

Fonction de coût (perte)

Nous avons une mesure d'erreur pour chaque élément individuel. Nous pouvons en tirer une métrique de qualité pour toute la ligne d'activation. Il est tout à fait naturel d'accepter, par exemple, que plus la somme des erreurs de tous les éléments de l'échantillon d'apprentissage est petite, mieux nous avons construit une ligne d'activation. Pour chaque élément individuel, l'erreur ne sera pas minimale, mais pour l'ensemble de l'échantillon de formation dans son ensemble, vous pouvez obtenir un compromis.

Mais vous pouvez prendre non pas une simple somme d'erreurs, mais la somme des erreurs au carré ( somme des erreurs au carré, somme des erreurs au carré, SSE ). Il est bien évident que, comme dans le cas de la somme des erreurs ordinaires, plus la ligne d'activation est proche des points avec les vraies classes d'éléments, plus la somme des erreurs quadratiques sera petite, mais dans le cas de l'erreur quadratique, les éléments les plus éloignés recevront une pénalité plus sévère.

En fait, ici, nous ne nous intéressons pas davantage à la pénalité pour les éléments éloignés, mais au fait que la fonction quadratique a un minimum et est différenciable partout (la somme habituelle aura un minimum, mais à ce minimum, elle ne sera pas différenciable), pourquoi avons-nous besoin de voir cela un peu plus tard.

Donc:

• Erreur - distance de la valeur d'étiquette de classe à l'hyperplan d'activation
• SSE - la somme des erreurs quadratiques de tous les éléments de l'échantillon d'apprentissage
• Fonction de coût $$$J (w)$ - métrique de qualité pour la ligne d'activation sélectionnée. Plus la valeur est basse, meilleure est l'activation.

Prendre en fonction de la valeur $$ SSE, dans le cas général d'un neurone linéaire, il ressemblera à ceci:

$$ $$\ begin {réunis} J (w) = {1 \ over 2} SSE = {1 \ over 2} \ sum _ {i = 1} ^ {n} (\ Phi (\ sum _ {j = 0} ^ {m} w_ {j} x_ {j} ^ {(i)}) - y ^ {(i)}) ^ {2} = {1 \ sur 2} \ sum _ {i = 1} ^ {n} (\ sum _ {j = 0} ^ {m} w_ {j} x_ {j} ^ {(i)} - y ^ {(i)}) ^ {2} \ end {réunis}$$

( $$ en premier lieu, il n'interfère pas avec SSE et, deuxièmement, pour plus de commodité - il sera magnifiquement réduit davantage

Ici $$$i$ - numéro d'élément, et $$$n$ - le nombre d'éléments dans l'ensemble de formation. Permettez-moi de vous rappeler que $$$y ^ {(i)}$ - vraie classe $$$i$ élément de l'échantillon d'apprentissage, c.-à-d. bonne réponse connue à l'avance.

Comme nous nous en souvenons, la position de la ligne d'activation est déterminée par les paramètres - facteurs de pondération $$$w$ donc vecteur $$$w$ agit comme un paramètre de la fonction de perte.

Pour boîtier 1 dimension

$$ $$J (w) = {1 \ over 2} SSE = {1 \ over 2} \ sum_ {i = 1} ^ {n} (w_ {0} + w_ {1} x_ {1} ^ {(i) } -y ^ {(i)}) ^ {2}$$

Les valeurs $$$x$ et $$$y$ sont connus à l'avance (il s'agit d'un ensemble de formation), ils sont donc fixes. Nous sélectionnons les paramètres $$$w$ , c'est-à-dire $$$w_0$ et $$$w_1$ de sorte que la valeur $$$J (w)$ Cela s'est avéré minime. Essayons de tracer le graphique comme une valeur $$$J (w)$ dépend des paramètres $$$w_0$ et $$$w_1$

 #      w0 = np.linspace(-10, 10, 200) w1 = np.linspace(-1, 1, 200) # https://docs.scipy.org/doc/numpy/reference/generated/numpy.meshgrid.html # https://stackoverflow.com/questions/36060933/matplotlib-plot-a-plane-and-points-in-3d-simultaneously ww0, ww1 = np.meshgrid(w0, w1) sse = [] for j in range(len(w1)): sse.append([]) for i in range(len(w0)): sse[j].append(((ww0[j][i]+ww1[j][i]*X1 - y)**2).sum()) sse = np.array(sse) # https://matplotlib.org/mpl_toolkits/mplot3d/tutorial.html # https://matplotlib.org/api/toolkits/mplot3d.html from mpl_toolkits.mplot3d import axes3d fig = plt.figure() ax = fig.add_subplot(111, projection='3d') ax.set_xlabel('w0') ax.set_ylabel('w1') ax.set_zlabel('J(w)') #ax.plot_surface(ww0, ww1, sse/2, color='lightblue', rstride=8, cstride=8) ax.plot_wireframe(ww0, ww1, sse/2, color='lightblue', rstride=8, cstride=8, label='SSE/2') plt.xlim(-10., 10.) plt.ylim(-1., 1.) plt.legend() plt.show() 

En général, on voit déjà ici que la fonction de perte a un minimum, et où elle se situe approximativement. Mais faisons une autre astuce et construisons le même graphique, uniquement avec une échelle verticale logarithmique .

 #ax.plot_surface(ww0, ww1, np.log(sse/2), color='lightblue', rstride=8, cstride=8) ax.plot_wireframe(ww0, ww1, np.log(sse/2), color='lightblue', rstride=8, cstride=8, label='log(SSE/2)') 

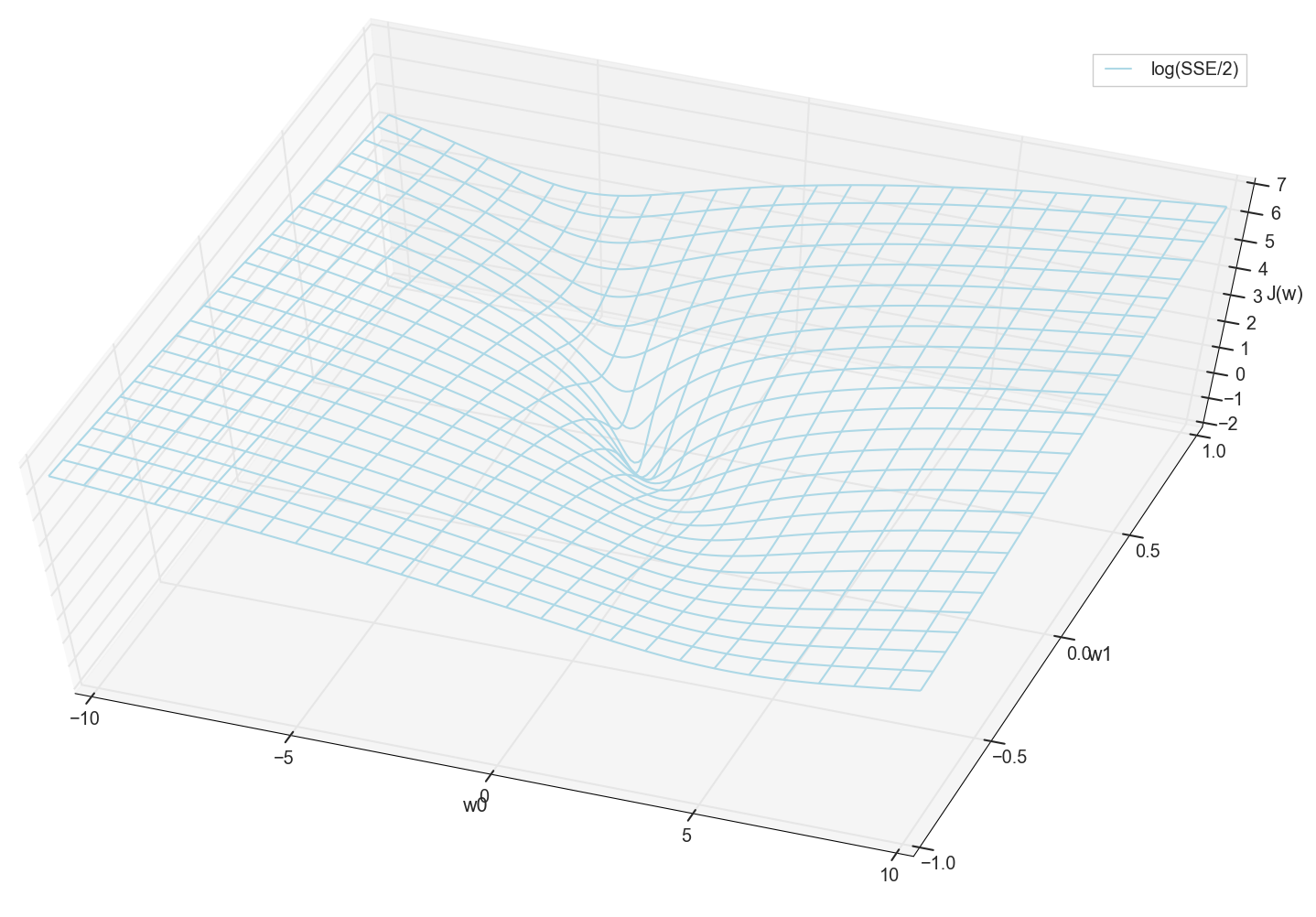
Je ne sais pas pour vous, mais personnellement, quand j'ai vu ce tableau pour la première fois, j'ai connu l'illumination. Cette cavité naturelle n'est pas seulement une visualisation figurative de collines multidimensionnelles d'un article populaire sur les réseaux de neurones, c'est un vrai graphique.

Notre tâche consiste à sélectionner ces valeurs $$$w_0$ et $$$w_1$ pour aller au fond de cette fosse. Nous obtenons les valeurs de poids - nous obtenons un neurone entraîné.

Puisque nous avons tout de même tracé un graphique et respecté personnellement son minimum, personne ne nous interdira de retrouver ses coordonnées par une simple énumération sur la grille "manuellement":

 #      # https://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.min.html # https://docs.scipy.org/doc/numpy/reference/generated/numpy.amin.html#numpy.amin # https://docs.scipy.org/doc/numpy/reference/generated/numpy.argmin.html min_ind = np.unravel_index(np.argmin(sse), sse.shape) #  -  #ax.scatter(ww0[min_ind], ww1[min_ind], sse[min_ind]/2, color='red', marker='o', s=100, ax.scatter(ww0[min_ind], ww1[min_ind], math.log(sse[min_ind]/2), color='red', marker='o', s=100, label='min: w0=%0.2f, w1=%0.2f, SSE/2=%0.2f' % (ww0[min_ind], ww1[min_ind], sse[min_ind]/2)) 

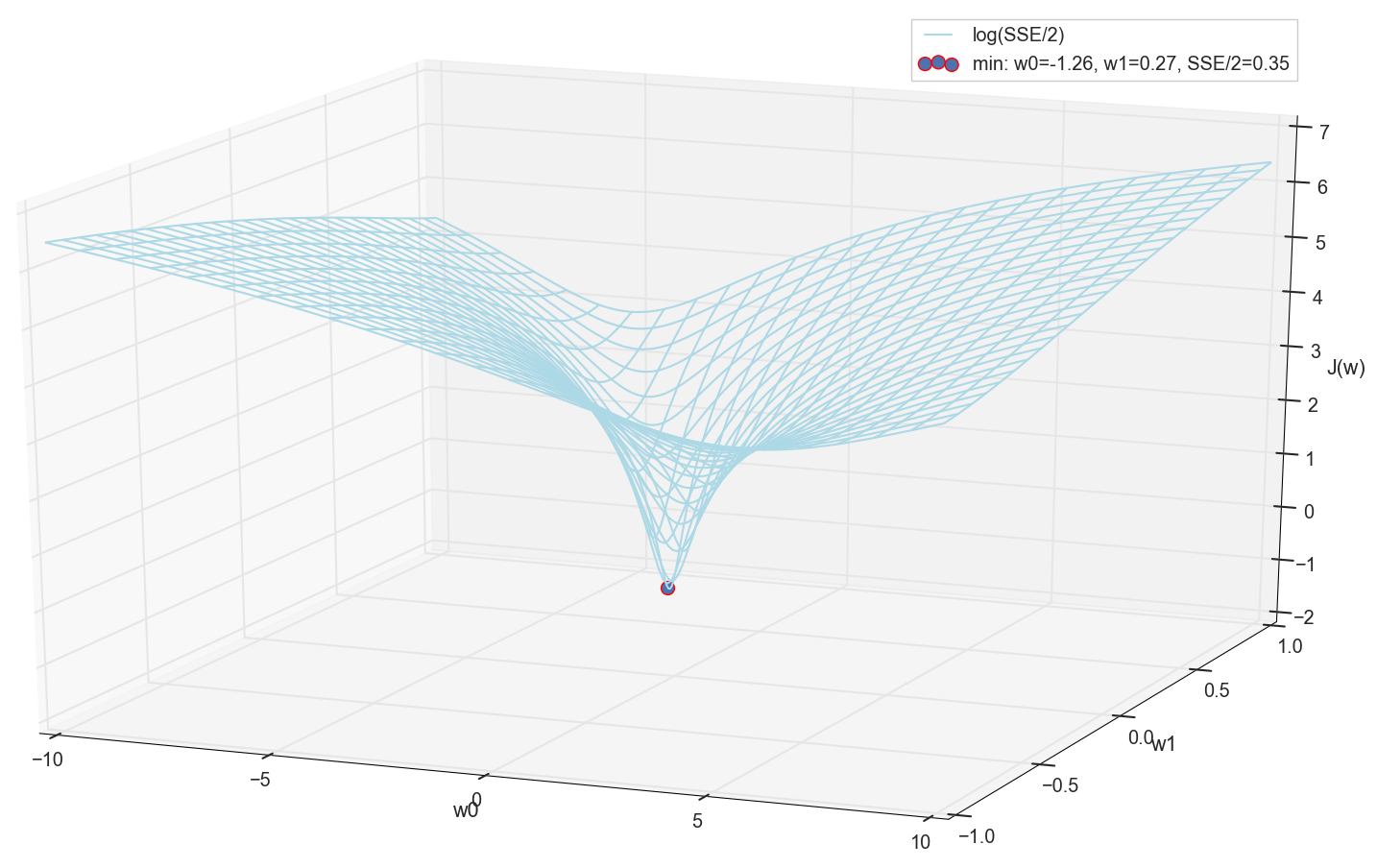
Ce sont les valeurs: $$$w_0 = -1,26$ et $$$w_1 = 0,27$ , la somme des erreurs carrées de l'ESS est de 0,69, la fonction de coût $$$J (w) = SSE / 2 = 0,35$ (plus précisément: 0,3456478371758288).

Voyons à quoi ressemble l'activation avec ces paramètres:

 #  ""   (SSE=0.69, sse/2=0.345) w0 = -1.26 w1 = 0.27 

Quant à moi, c'est tout à fait normal. Le point d'intersection d'activation avec un seuil zéro sépare les éléments de différentes classes, et l'activation elle-même leur attribue les valeurs correctes. Dans le même temps, l'activation semble être dans une position optimale.

Avant de continuer, nous admirons à nouveau le graphique sur la grille plus large:

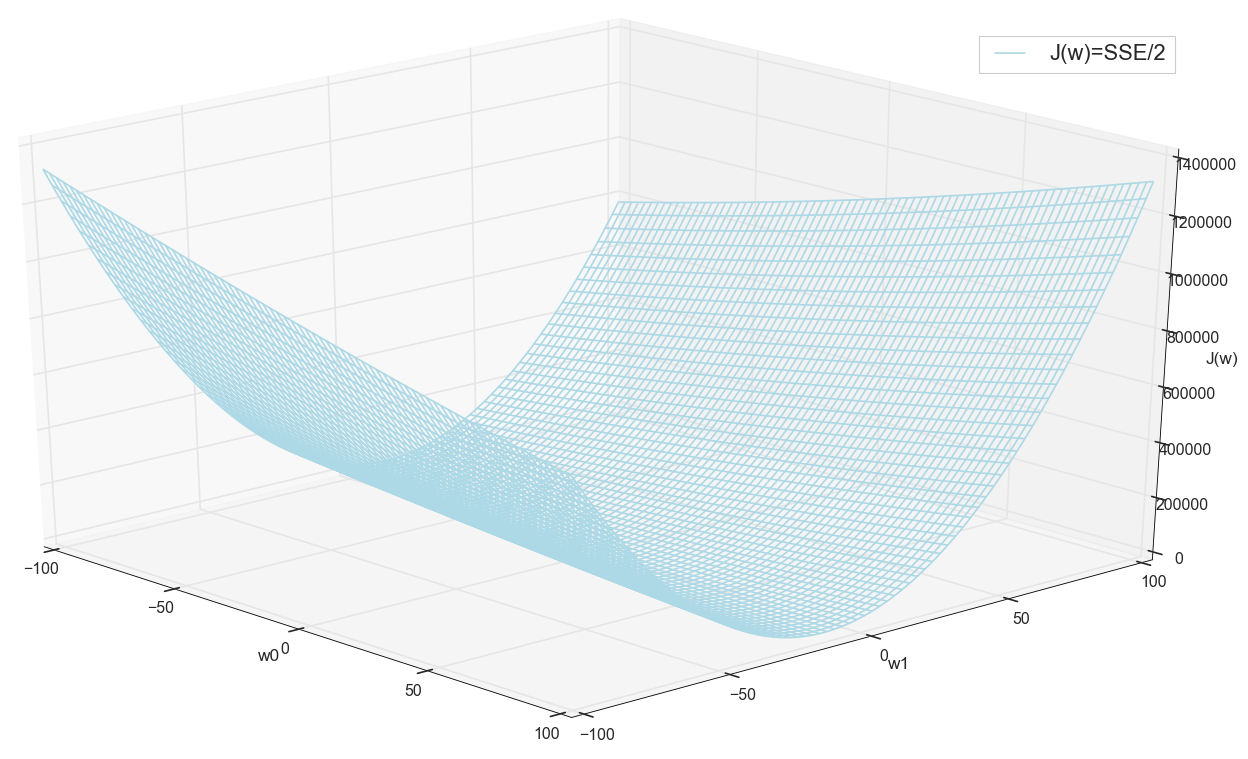
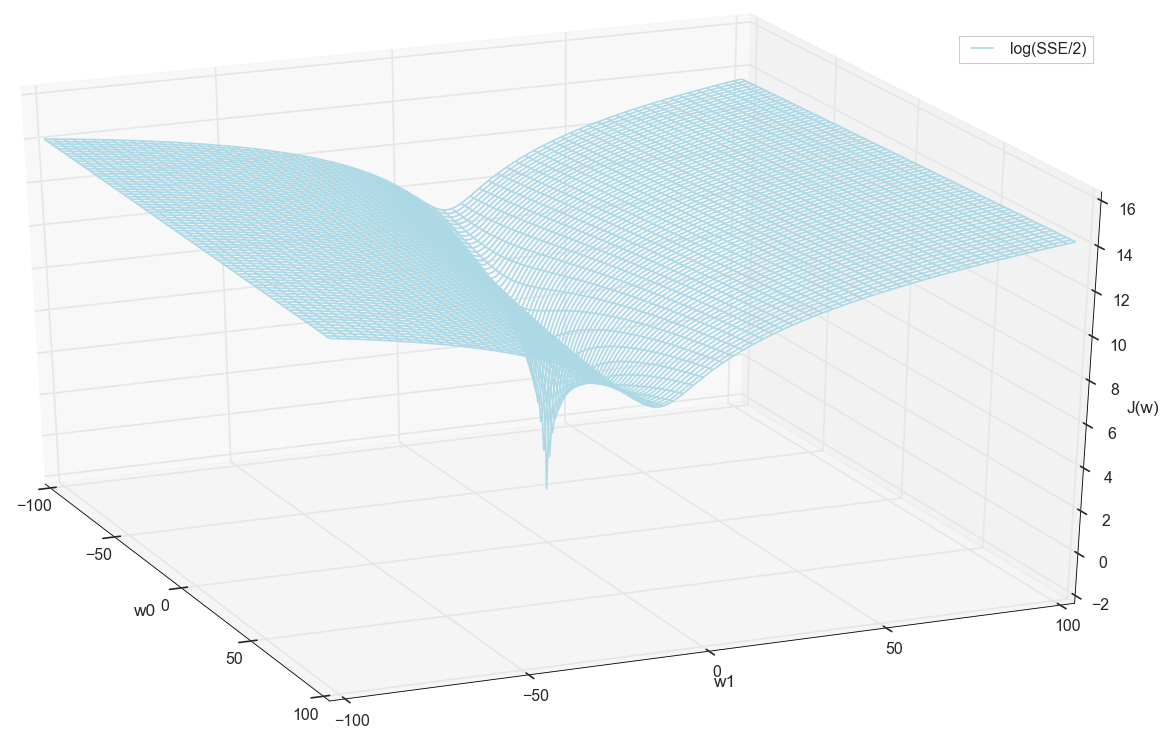
Il semble qu'il n'y ait pas d'autres bas à proximité qui auraient pensé.

Recherche minimale

Nous avons donc obtenu des poids - les coordonnées de la valeur d'erreur minimale. Ce sera la valeur optimale des poids sur l'échantillon d'apprentissage. D'une manière générale, c'est exactement ce dont nous avons besoin, on peut dire que le neurone est entraîné. Peut-être que cela peut être terminé?

Rechercher un minimum: recherche par grille

• L'option à première vue fonctionne très bien (comme nous le voyons)
• Vous devez savoir à l'avance la zone où chercher un minimum (vous pouvez prendre des bordures assez grandes, puis rétrécir la zone de recherche - ce n'est que par l'œil)
• Pour augmenter la précision, vous devez diminuer le pas → encore plus de points (solution: vous pouvez restreindre de manière itérative la zone de recherche)
• Trop de points (pour 2d cela peut être correct, mais pour les cas multidimensionnels nous rencontrons des ressources très rapidement)
• Pour MNIST (28x28 = 784 pixels - le même nombre d'entrées, les mêmes facteurs de pondération plus le décalage, une grille de 100 pas par dimension): 100 ^ 785 = 10 ^ 1570.

Donc, si nous voulons entraîner un seul neurone (pas même un réseau de neurones) dans une image de 28x28 = 784 pixels en recherchant un minimum par dénombrement direct sur une grille de 100 points pour chaque mesure, nous devons trier 10 ^ 1570 combinaisons. C'est beaucoup pour le stockage et la recherche (dans la partie visible de l'Univers, il n'y a que 10 ^ 80 atomes, l'Univers existe pendant environ 4 * 10 ^ 17 secondes = 4 * 10 ^ 26 nanosecondes).

Essayons de trouver une option plus rapidement.

Recherche minimale: descente à pas constant

Regardons le graphique de la fonction de perte $$$J (w)$ dans l'avion: correction $$$w_0$ changer $$$w_1$

 def sse_(X, y, w0, w1): return ((w0+w1*X - y)**2).sum() #  w0,   J(w1)=sse(w1)/2 w1 = np.linspace(-1, 1, 200) sse = [[], [], []] for i in range(len(w1)): sse[0].append(sse_(X1, y, -1, w1[i])) sse[1].append(sse_(X1, y, 0, w1[i])) sse[2].append(sse_(X1, y, 1, w1[i])) sse = np.array(sse) plt.plot(w1, sse[0]/2, color='orange', label='w0=-1') plt.plot(w1, sse[1]/2, color='blue', label='w0=0') plt.plot(w1, sse[2]/2, color='red', label='w0=1') plt.xlabel('w1') plt.ylabel('J(w)') plt.legend() plt.show() 

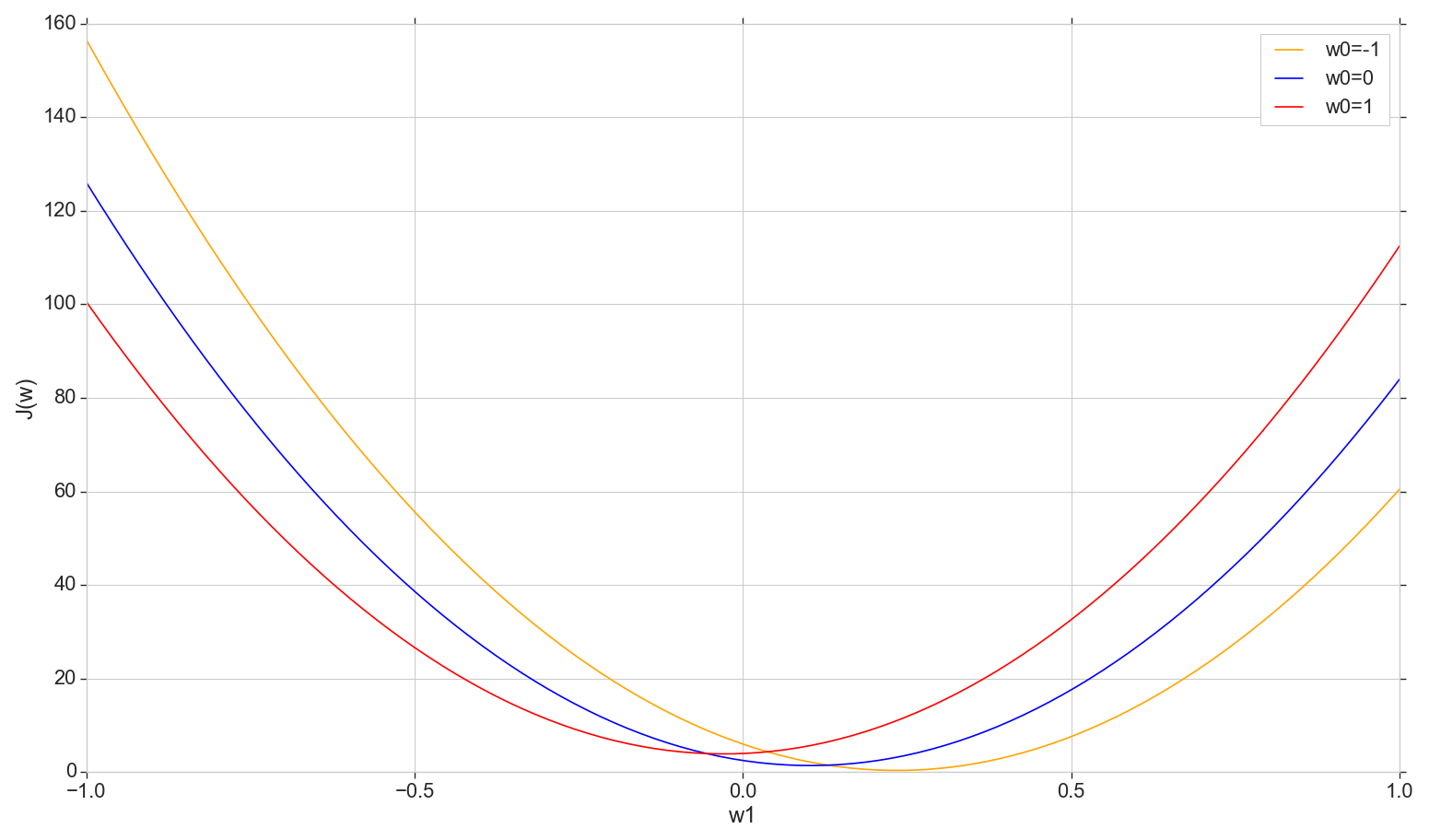
Il s'agit d'une parabole ordinaire (plus précisément, une famille de paraboles - elles différeront légèrement selon le type de valeur sur lequel $$$w_0$ ) Pour trouver la parabole minimale, il n'est pas nécessaire de trier tous les points. Nous pouvons choisir un point arbitraire sur l'axe horizontal et nous déplacer vers le minimum d'un pas.

Envisagez une option à pas constant

• Si le pas est trop grand, vous pouvez le manquer et ne pas atteindre le minimum (le pas peut être réduit)
• S'il est trop petit, il y aura trop d'étapes (plus qu'il ne pourrait l'être)
• Dans tous les cas, nous n'atteindrons pas le minimum exact, mais nous pouvons l'atteindre avec une précision arbitraire en modifiant le pas près du minimum inexact trouvé (le pas cesse d'être constant)
• Nous ne connaissons pas le sens de la descente (il est possible de résoudre algorithmiquement: ne pas marcher dans le sens d'une erreur croissante)
• Le problème avec la recherche de la plage a été résolu (vous pouvez descendre de n'importe où - tôt ou tard, nous descendrons de toute façon)
• En principe, l'option fonctionne, mais peut-être y a-t-il une meilleure option?

Remarque: lorsque j'ai parlé d'une telle option de descente à une conférence, un étudiant a demandé pourquoi vous devez vous déplacer par étapes si vous pouvez immédiatement trouver une parabole minimale en utilisant la formule? Au début, j'ai répondu à quelque chose dans l'esprit que nous sommes maintenant intéressés à considérer l'option d'itération, afin que plus tard nous puissions l'utiliser non seulement avec une parabole, mais aussi dans d'autres situations. De plus, en fait, nous n'avons pas besoin d'au moins une parabole spécifiquement sur cette section - nous allons passer au minimum non pas dans une dimension, mais dans toutes les dimensions de telle manière qu'à chaque nouvelle itération une nouvelle étape aura lieu non pas le long de cette parabole, mais sur parabole avec une nouvelle tranche avec une valeur décalée $$$w_0$ . Mais en réfléchissant plus tard, j'ai pensé qu'en principe, il n'y a rien de mal à se déplacer à chaque tranche, pas par étapes, mais à descendre immédiatement au minimum de la tranche actuelle. Ainsi, maintes et maintes fois, mesure par mesure, nous devons encore glisser au minimum global, et cela semble plus rapide que les étapes. Pour un seul neurone, cela devrait fonctionner, et pas seulement avec une parabole. Mais je n'ai pas encore commencé à perdre du temps à tester cette théorie, alors ici nous allons simplement de l'avant - j'ai promis de parler de descente de gradient.

Rechercher un minimum: descente en pente

En général, nous descendons les étapes, mais nous le faisons plus intelligemment. Nous utilisons la dérivée de la courbe de coût pour sélectionner l'étape (ici, pas la courbe de coût , mais la courbe de coût ).

• Nous avons plusieurs dimensions et chacune a sa propre courbe: on fixe tout $$$w_j$ sauf $$$w_k$ ,
• $$$J (w_k)$ il y aura une courbe d'erreur dans $$$k$ e dimension
• Tous sont (dans notre cas) des paraboles, mais, d'une manière générale, il est seulement important qu'ils soient différenciables partout et aient un minimum
• Pour ajuster le pas dans chaque mesure, nous utiliserons la dérivée partielle de la fonction d'erreur par rapport à cette mesure (un coefficient variable $$$w_k$ )
• Un vecteur de ces dérivées partielles est appelé gradient.

Tout cela est bien, mais d'où vient le dérivé? Voyons maintenant.

La signification géométrique de la dérivée

Pour moi, le dérivé est resté pendant longtemps un ensemble de formules spéciales et de règles pour son calcul, plus quelque chose sur l'augmentation, la diminution et les extrêmes. Il conviendra ici de rappeler ou de découvrir ce qu'est réellement le dérivé.

Fonction dérivée $$$y (x)$ à ce stade $$$x_0$ Est la limite du rapport de l'incrément de la fonction $$$\ Delta y$ à incrément d'argument $$$\ Delta x$ lors de l'incrémentation d'un argument $$$\ Delta x$ tendant vers zéro:

$$ $$y '(x_0) = \ lim _ {\ Delta x \ to 0} {\ Delta y \ over \ Delta x}, \ Delta y = y (x_0 + \ Delta x) - y (x_0)$$

Le point dans l'image $$$M (x_0, y (x_0)) = (x_0, y_0)$ Est le point auquel nous voulons déterminer la dérivée. Point $$$N (x_0 + \ Delta x, y (x_0 + \ Delta x)) = (x_0 + \ Delta x, y_0 + \ Delta y)$ - point obtenu en incrémentant l'argument $$$\ Delta x$ . Direct $$$Mn$ - sécante passant par ces deux points.

Point $$$A$ - intersection de sécante $$$Mn$ avec axe horizontal $$$y = 0$ .

Considérons deux triangles rectangles: un triangle $$$\ triangle NPM$ avec section sécante $$$Mn$ comme une hypoténuse et un triangle $$$\ triangle MBA$ avec la continuation de la sécante à l'axe $$$y = 0$ - segment $$$AM$ comme hypoténuse. D'après le cours sur le graphique et la géométrie de l'école, il est évident que les angles $$$\ angle NMP$ et $$$\ angle MAB$ sont égaux, et donc leurs tangentes sont égales:

$$ $$\ tan \ angle MAB = \ tan \ angle NMP = {MB \ over AB} = {NP \ over MP} = {\ Delta y \ over \ Delta x}$$

Ajouter à l'image: $$$MD$ - tangente à la courbe initiale au point $$$M$ traverse un axe $$$y = 0$ au point $$$D$ . Triangle $$$\ triangle MBD$ - un triangle rectangle avec hypoténuse - section cassette, segment $$$MD$ .

Nous visons l'incrément $$$\ Delta x$ à zéro:

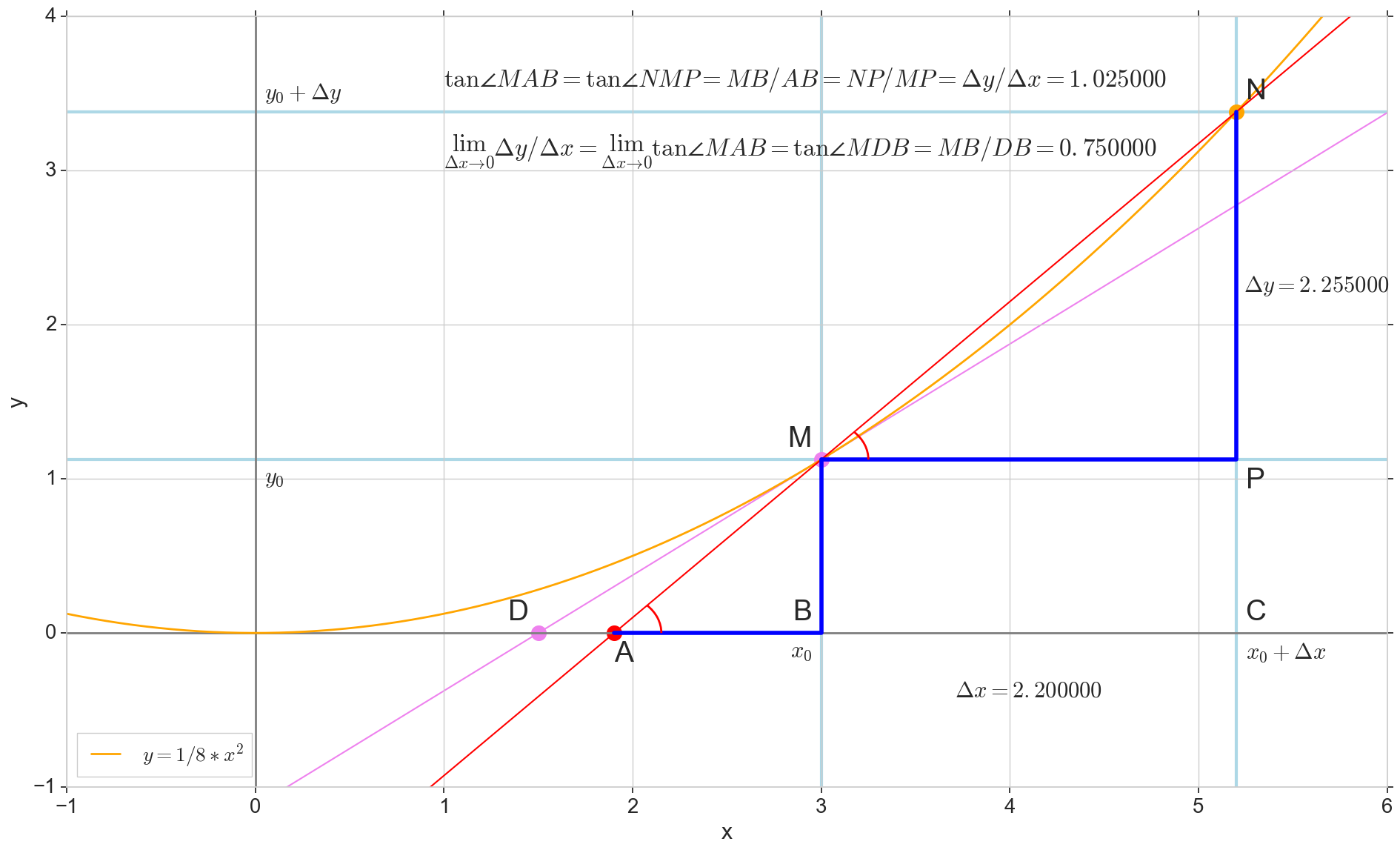
Point $$$N$ passer au point $$$M$ par fonction, point $$$A$ rampe à un point $$$D$ le long de l'axe $$$y$ sécante $$$Mn$ se transforme en tangente $$$MD$ avec point de contact $$$M$ . Triangle source $$$\ triangle NPM$ avec des jambes $$$\ Delta x$ et $$$\ Delta y$ rétrécit à un point, mais un triangle comme ça $$$\ triangle MBA$ se transforme en triangle $$$\ triangle MBD$ préservant non seulement les dimensions macroscopiques, mais aussi l'égalité des angles $$$\ angle MAB$ et $$$\ angle NMP$ .

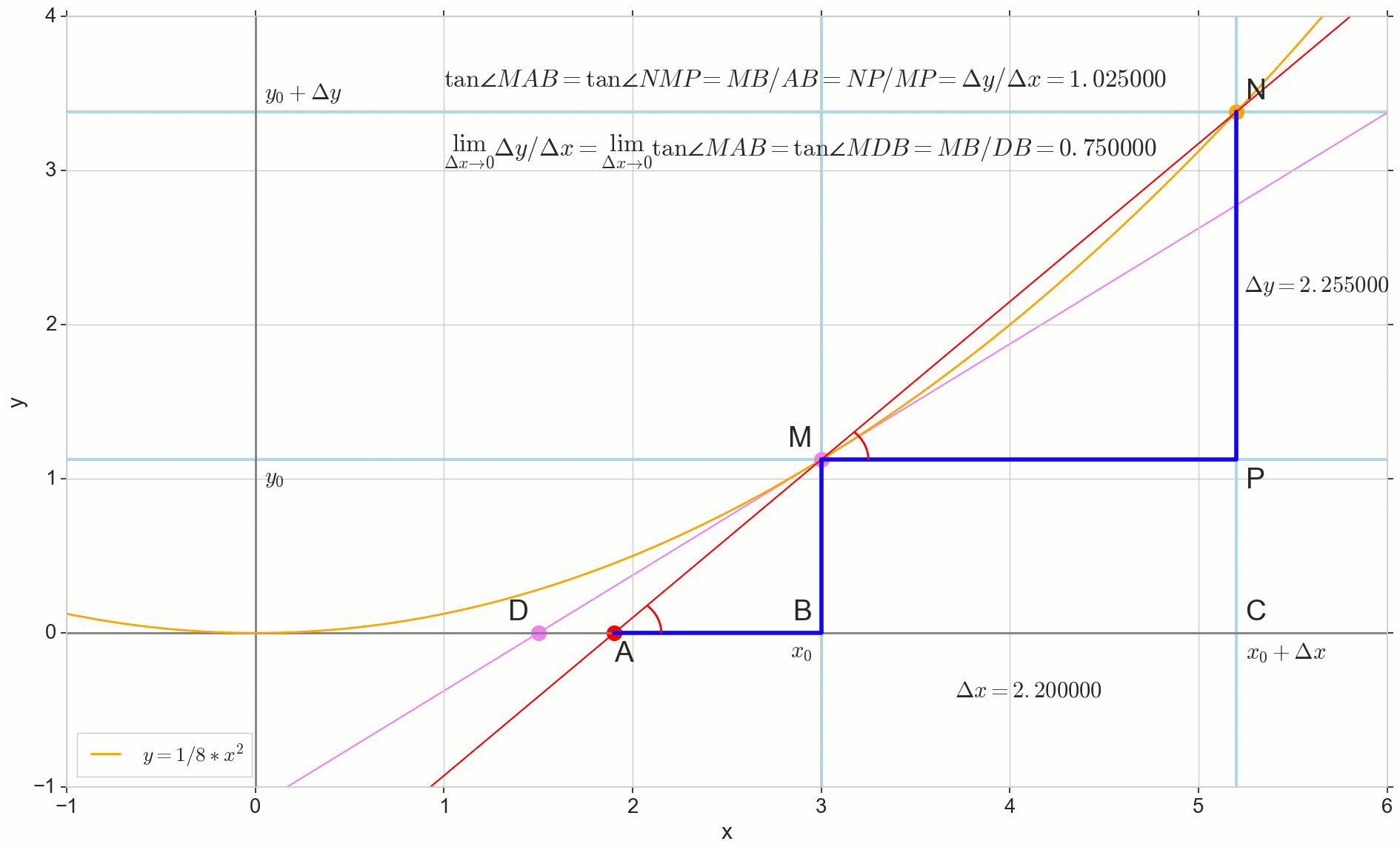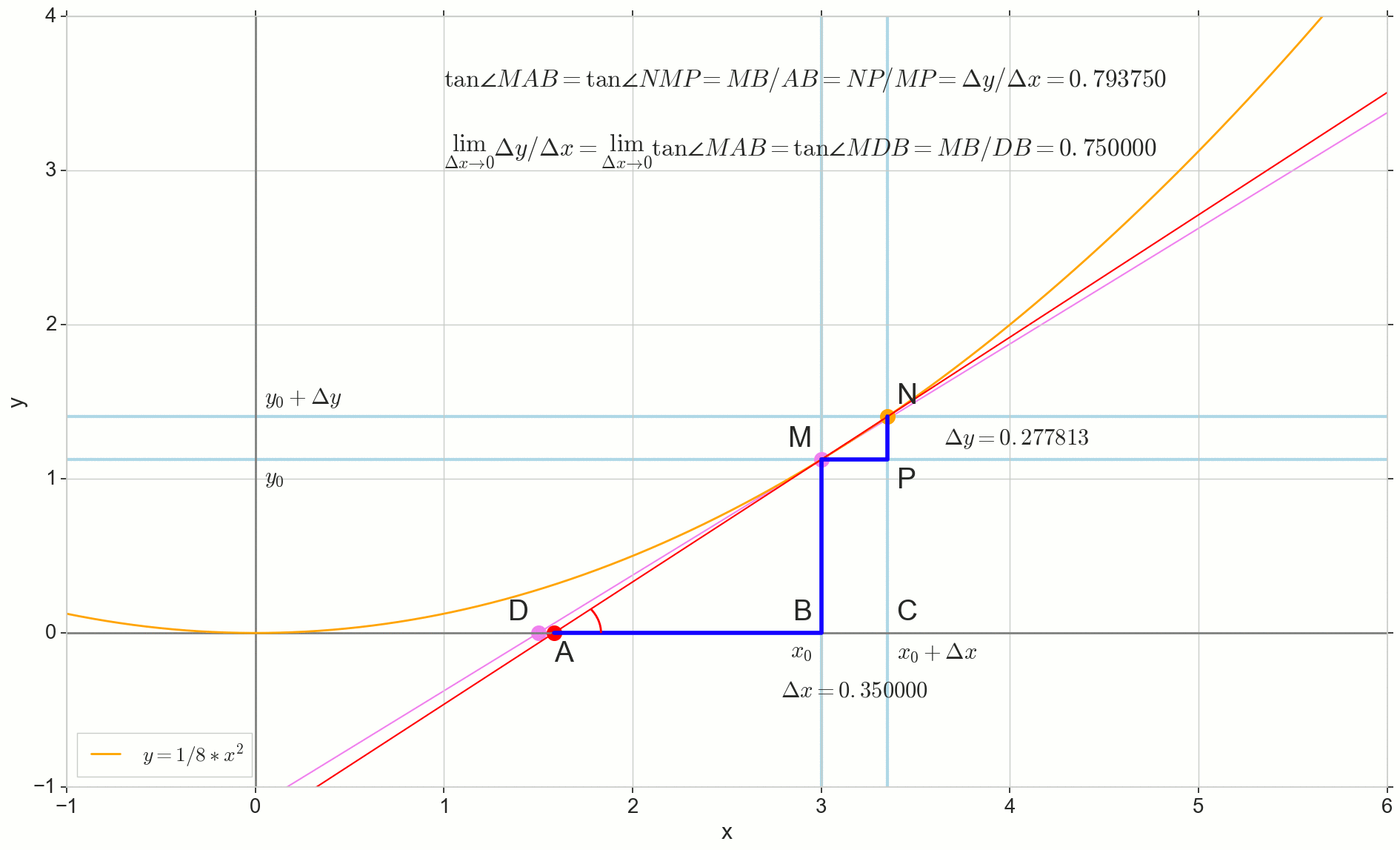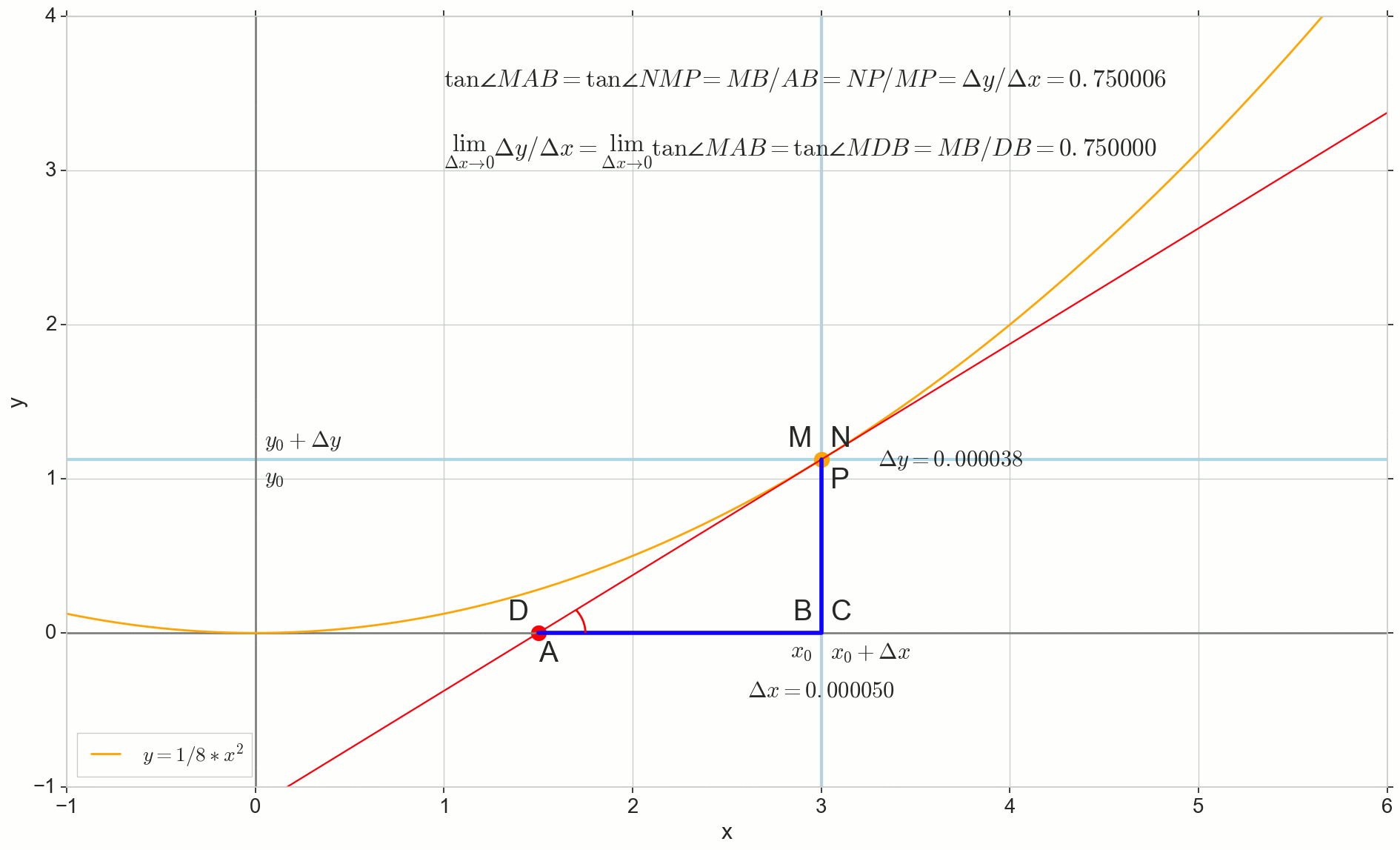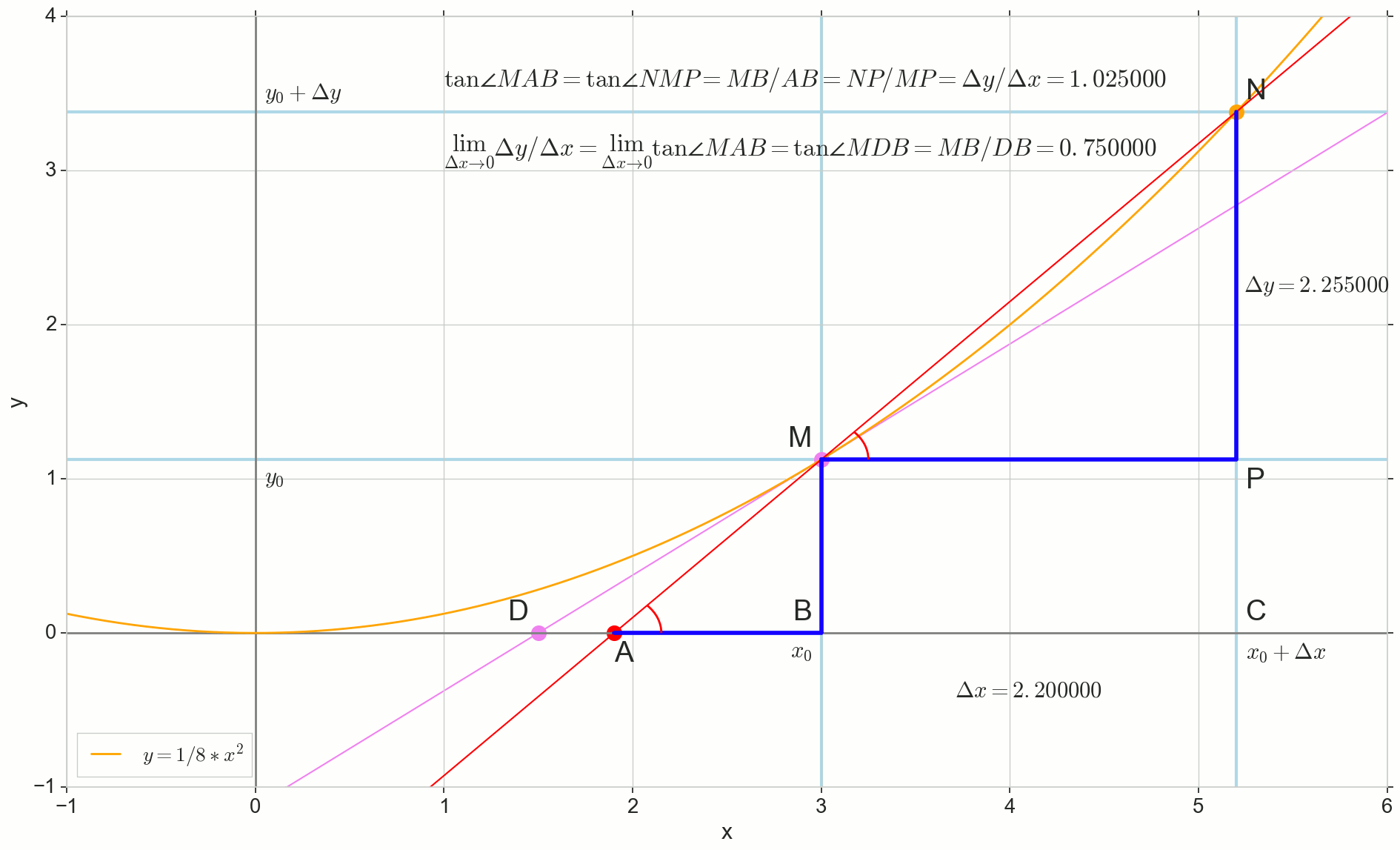
Comment incrémenter $$$\ Delta x$ , se rapprochant infiniment de zéro, n'atteindra jamais zéro, donc le point $$$N$ ne jamais arriver à l'endroit exact $$$M$ pointer $$$A$ n'atteindra pas le point $$$D$ triangle $$$\ triangle MBA$ ne se transformera pas en $$$\ triangle MBD$ . , , «» $$$\lim$ .

$$$\triangle MBA$ — $$$\triangle MBD$ , :

$$ $$\lim_{\Delta x \to 0}{\Delta y \over \Delta x} = \lim_{\Delta x \to 0}{\tan \angle NMP} = \lim_{\Delta x \to 0}{\tan \angle MAB} = \lim_{\Delta x \to 0}{MB \over AB} = {MB \over DB} = \tan \angle MDB$$

:

$$ $$\lim_{\Delta x \to 0}{\Delta y \over \Delta x} = \tan \angle MDB$$

, , :

$$ $$y'(x_0) = \lim_{\Delta x \to 0}{\Delta y \over \Delta x} = \tan \angle MDB$$

, $$$y=0$ . .

, , , , , . , , , , .. ( , , ). : , (, — tangent line , , — ).

:

• $$$x_0$ $$$y=0$
• — $$$y(x_0)$ — $$$x_0$ $$$y=0$ $$$y=0$
• «» , ,
• — : — , —
• ( , , , $$$\Delta y$ )

, , :

— , — $$$x_0$ , — . — — . — $$$y=0$ , — .

, , , , . ( , ) (: $$$y=0$ , ).

( ): , (: $$$y=0$ , ).

, : (), «»/«» , . — . , , ? .

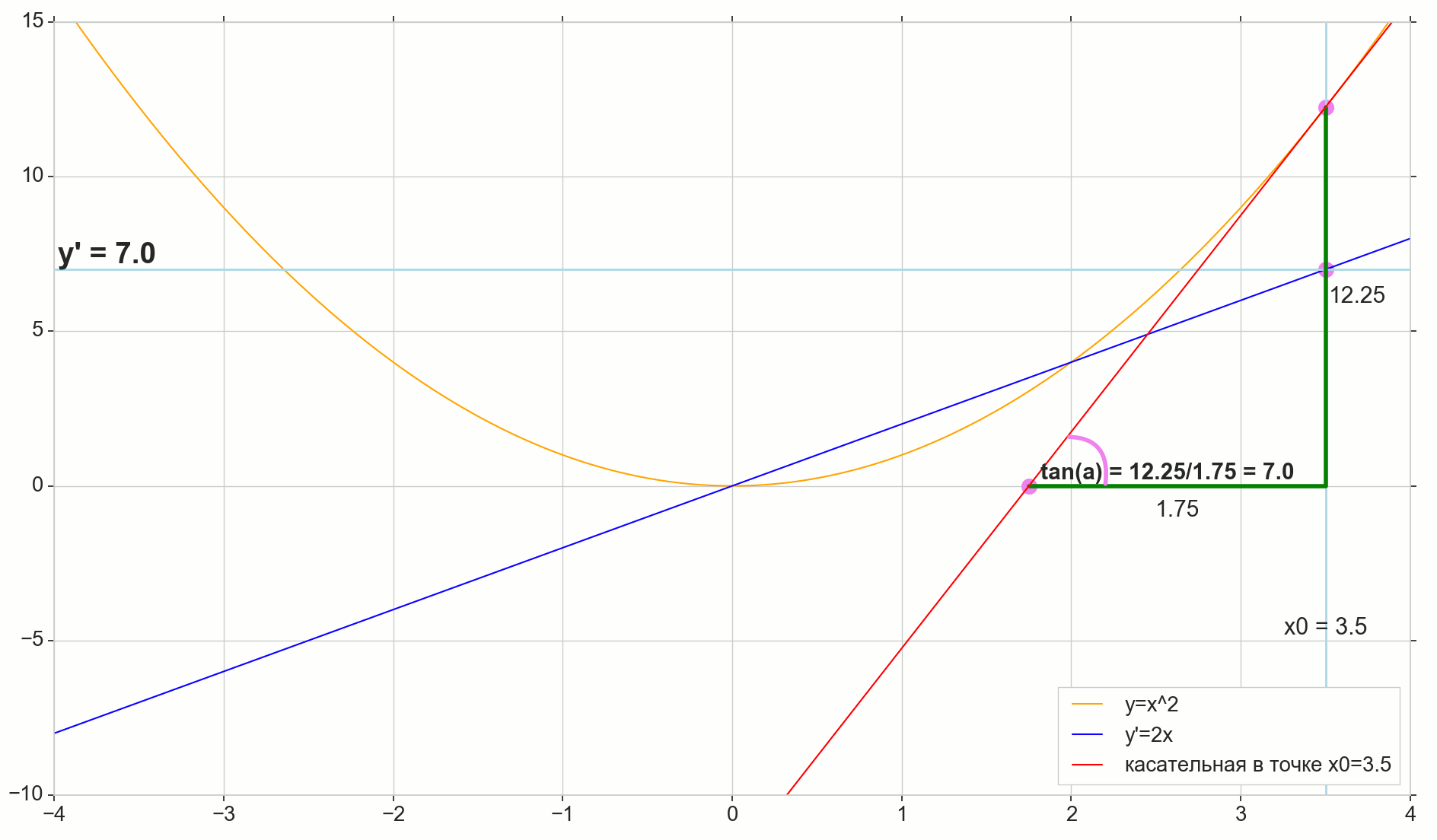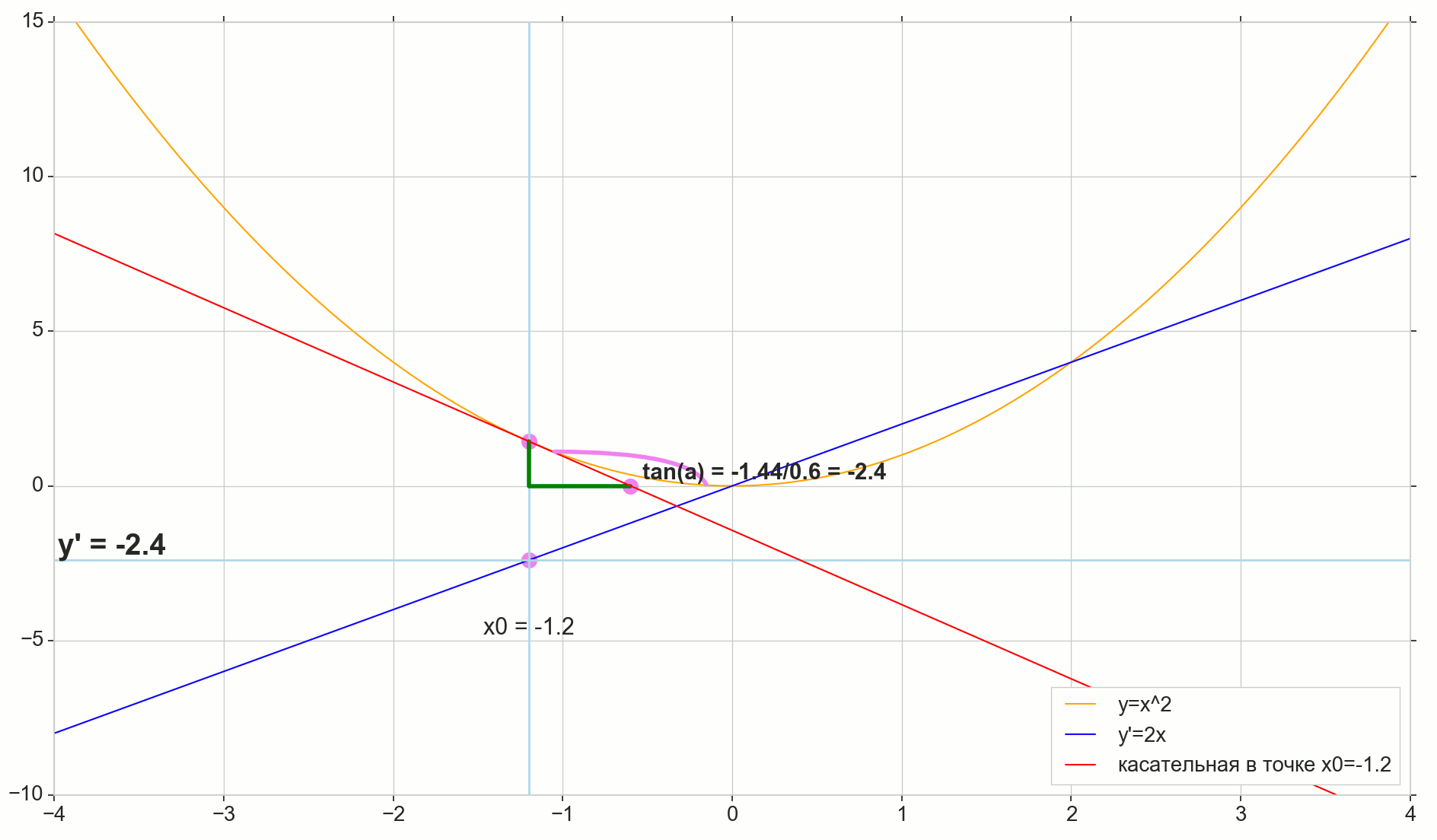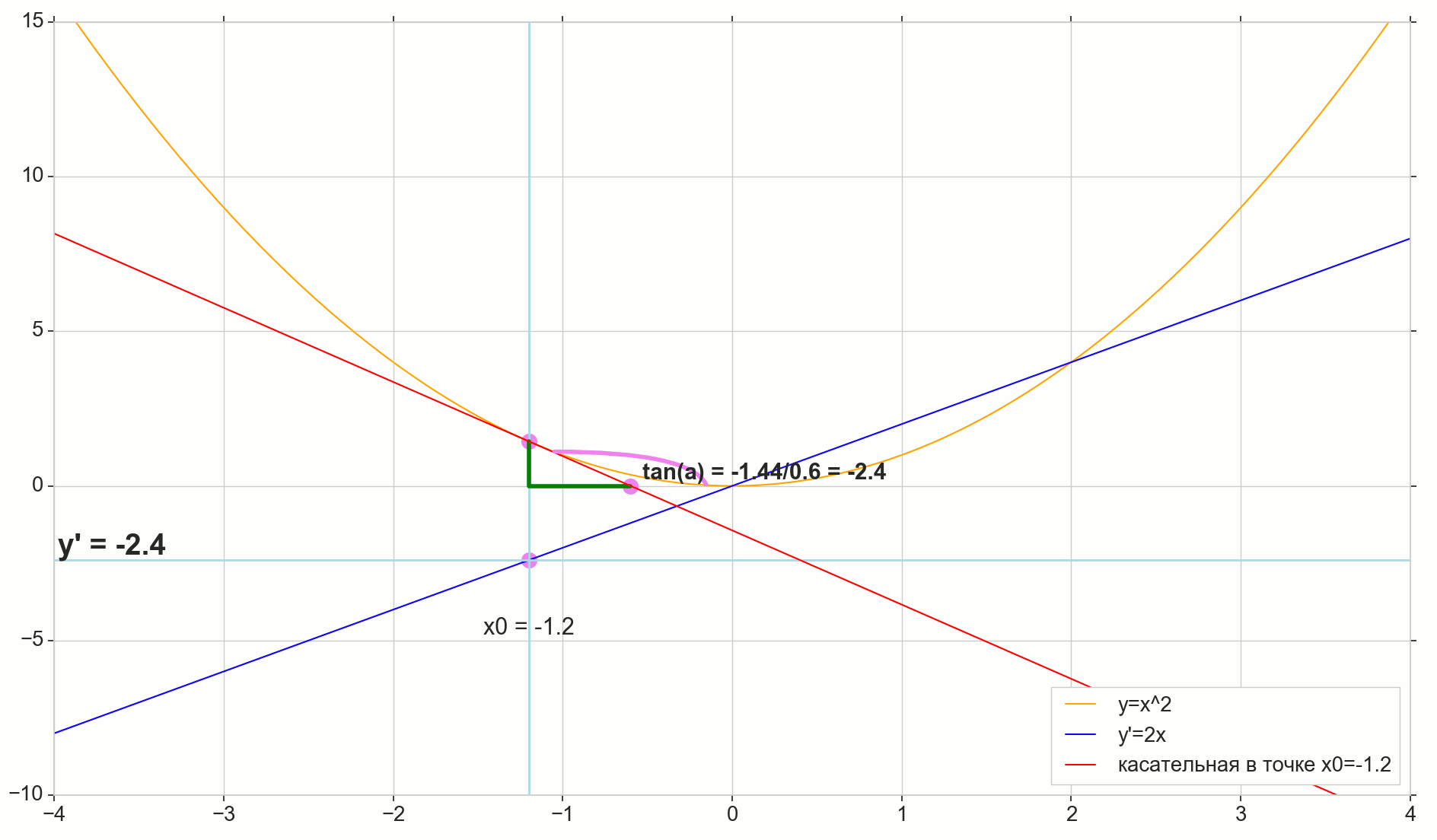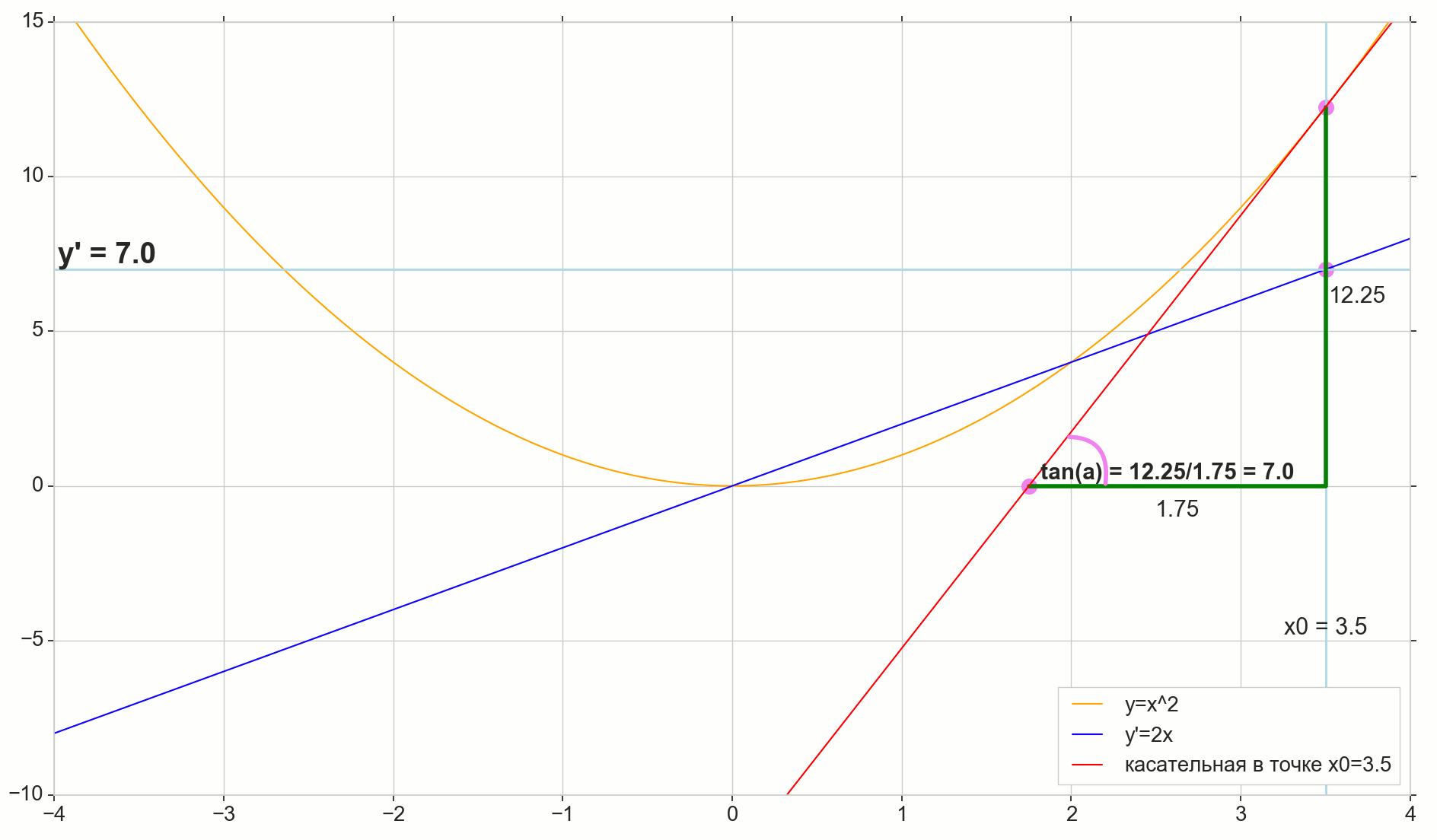
$$$J(w)$ . , , , .

$$ $$J(w)={1 \over 2} SSE ={1 \over 2}\sum _{i=1}^{n}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})^{2}$$

• $$$k$ -
• ,

$$ $$\begin{gathered}\frac{\partial J(w)}{\partial w_{k}} ={\frac{\partial }{\partial w_{k}}}{1 \over 2}\sum _{i=1}^{n}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})^{2} ={1 \over 2}\sum _{i=1}^{n}{\frac{\partial }{\partial w_{k}}}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})^{2} \\={1\over 2}\sum _{i=1}^{n}2(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)}) \frac{\partial }{\partial w_{k}}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)}) \\={1\over 2}2\sum _{i=1}^{n}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)}) \frac{\partial }{\partial w_{k}}((w_{0}x_{0}^{(i)}+...+w_{k}x_{k}^{(i)}+...+w_{m}x_{m}^{(i)}) - y^{(i)}) \\=\sum _{i=1}^{n}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})x_{k}^{(i)} \end{gathered}$$

, : , , , ( ) . , $$$w_k$ ( , ), . , , , $$$1/2$ SSE .

:

$$ $$\begin{gathered}\frac{\partial J(w)}{\partial w_{k}} =\sum _{i=1}^{n}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})x_{k}^{(i)} \end{gathered}$$

— ( $$$\nabla$ [], , .. []):

$$ $$\nabla J(w)=(\frac{\partial J(w)}{\partial w_{0}},...,\frac{\partial J(w)}{\partial w_{m}}), w=(w_{0},...,w_{m})$$

:

$$ $$w:=w+\Delta w, \Delta w=-\eta \nabla J(w)$$

$$$k$ - :

$$ $$w_{k}:=w_{k}+\Delta w_{k}, \Delta w_{k}=-\eta \frac{\partial J(w)}{\partial w_{k}}$$

:

• $$$\eta$ [] — ,

, , , . , .

1- :

$$ $$\Phi(x, w)=w_0+w_1x_1$$

( ):

$$ $$\frac{\partial J(w)}{\partial w_{0}} =\sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})x_{0}^{(i)} =\sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})$$

$$ $$\frac{\partial J(w)}{\partial w_{1}}= \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})x_{1}^{(i)}$$

:

$$ $$\Delta w_{0}=-\eta \frac{\partial J(w)}{\partial w_{0}}=-\eta \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})$$

$$ $$\Delta w_{1}=-\eta \frac{\partial J(w)}{\partial w_{1}}=-\eta \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})x_{1}^{(i)}$$

, . .

( $$$w_1$ )

$$$w_0=1$ , $$$J(w_1)$

$$$X$ ( ) $$$y$ $$$w_0$ et $$$w_1$ ( ):

 def sse_(X, y, w0, w1): return ((w0+w1*X - y)**2).sum() 

$$$w_1$ -1.5 1.5.

  #      w0 = 1 w1 = np.linspace(-1.5, 1.5, 200) #              numpy.dot # https://docs.scipy.org/doc/numpy/reference/generated/numpy.dot.html #    ,      sse = [] for i in range(len(w1)): sse.append(sse_(X1, y, w0, w1[i])) sse = np.array(sse) 

, ( , , ):

  plt.subplot(3,1,1) # sse plt.plot(w1, sse/2, color='red', label='w0=1') #  -   w1_first = .9 plt.scatter(w1_first, sse_(X1, y, w0, w1_first)/2, color='blue', marker='o', s=100) plt.xlim(-1.2, 1.2) plt.xlabel(u'w1') plt.ylabel(u'J(w1, w0=1)') plt.legend(loc='lower left') 

, , $$${\delta J(w)} \over {\delta w_1}$ — :

  grad_w1 = [] for i in range(len(w1)): grad = ((w0 + w1[i]*X1 - y)*X1).sum() grad_w1.append(grad) plt.subplot(3,1,3) plt.plot(w1, grad_w1, label=u' ∂J(w)/∂w1') plt.xlim(-1.2, 1.2) plt.xlabel(u'w1') plt.ylabel(u'∂J(w)/∂w1') plt.legend(loc='upper left') 

$$$\Delta w_1(w_1)$ (, $$$\Delta w_1$ $$$w_1$ , .. , ):

  eta = 0.001 delta_w1 = [] for i in range(len(w1)): grad = ((w0 + w1[i]*X1 - y)*X1).sum() delta = -eta*grad delta_w1.append(delta) plt.subplot(3,1,2) plt.plot(w1, delta_w1, color='orange', label=u'Δw1, η=%s'%eta) plt.xlim(-1.2, 1.2) plt.xlabel(u'w1') plt.ylabel(u'Δw1=-η*∂J(w)/∂w1') plt.legend(loc='upper right') 

  plt.show() 

• : ,
• : — «» ( , «» ),
• : — ( ), $$$\eta$ [] ( ),

: , 1000 .

, ,

$$$w$ — - - . $$$w_0=1$ , $$$w_1=0.9$ . $$$\eta=0.001$ ( , ) 12:

  #    12-14  eta = 0.001 epochs = 12 

:

  #      w1_epochs = [w1_first] delta_w1_epochs = [] w1_next = w1_first for i in range(epochs): grad = ((w0 + w1_next*X1 - y)*X1).sum() delta = -eta*grad w1_next = w1_next + delta delta_w1_epochs.append(delta) w1_epochs.append(w1_next) #   - 0 delta_w1_epochs.append(0) w1_epochs = np.array(w1_epochs) delta_w1_epochs = np.array(delta_w1_epochs) #     sse_epochs = [] for i in range(len(w1_epochs)): sse_epochs.append(sse_(X1, y, w0, w1_epochs[i])) sse_epochs = np.array(sse_epochs) 

$$$w_1$ $$$J(w_1, w_0=1)$ :

  #     -       size_epochs = [10 + (250-100)*epoch/epochs for epoch in reversed(range(epochs+1))] plt.scatter(w1_epochs, sse_epochs/2, color='blue', marker='o', s=size_epochs, label=u'  , η=%s'%eta) #    w1 plt.plot([w1_epochs, w1_epochs+delta_w1_epochs], [sse_epochs/2, sse_epochs/2], color='orange')#, label='Δw1') 

$$$\Delta w_1(w_1)$

 plt.scatter(w1_epochs, delta_w1_epochs, color='blue', marker='o', s=size_epochs, label=u'  , η=%s'%eta) plt.plot([w1_epochs, w1_epochs], [delta_w1_epochs, np.zeros(len(delta_w1_epochs))], color='orange') 

, , ( ), . , , , .

: , , , «» , — , .

• — $$$w_1$ , —
• , $$$w_1$
• — : , —
• , —
• , ( ), , ( ) — , —
• ( , — ).
• : — , —
• ? — . .
• . $$$w_1$ , . , «»/«» . , , . , , , « ». , : $$$w_1=0.9$ 200, , , , 1. , , , . — $$$\eta$ . , 200 1. $$$\eta=0.001$ , $$$w_1=0.9$ 200*0.001=0.2 ( -1, -0.2) — .
• $$$J(w_1=0.9)=92.43$ , 12 (, ) $$$J(w_1=0.03)=8.54$
• , ,

, . , . , ( , ). $$$\eta$ , .

: , , , .

, , , .

$$$\eta$

• $$$\eta$ [] — ()
• ,
• «»: , , ,
• , $$$J(w)$
• : $$$w_k$ , $$$\eta$ , $$$w_k$

$$$\eta=0.01$

 #    eta = 0.01 epochs = 6 

. , . 3- , 3- , , .. , .. . , , [] .

$$$\eta$ $$$J(w)$ $$$\eta$

  #      J(w0, w1)   w0  w1 #    12-14  eta = 0.001 epochs = 12 #  -   #   w0  w1 -  ,   , #    10-15  # NB: (    , , ,  , #      ) w0_first = -.9 w1_first = -.9 #      w0_epochs = [w0_first] w1_epochs = [w1_first] delta_w0_epochs = [] delta_w1_epochs = [] w0_next = w0_first w1_next = w1_first for i in range(epochs): grad_w0 = (w0_next + w1_next*X1 - y).sum() delta_w0 = -eta*grad_w0 grad_w1 = ((w0_next + w1_next*X1 - y)*X1).sum() delta_w1 = -eta*grad_w1 w0_next = w0_next + delta_w0 w1_next = w1_next + delta_w1 delta_w0_epochs.append(delta_w0) delta_w1_epochs.append(delta_w1) w0_epochs.append(w0_next) w1_epochs.append(w1_next) #     sse_epochs = [] for i in range(len(w1_epochs)): sse = sse_(X1, y, w0_epochs[i], w1_epochs[i]) sse_epochs.append(sse) print('epoch=%d, w0=%f, w1=%f, SSE/2=%f' % (i, w0_epochs[i], w1_epochs[i], sse/2)) sse_epochs = np.array(sse_epochs) #  -      η (--) plt.plot(range(len(sse_epochs)), sse_epochs, label=u'J(w)=SSE/2, η=%s'%eta) plt.xlabel(u'epoch (η=%s)'%eta) plt.ylabel(u'J(w)') plt.legend(loc='upper right') plt.show() 

: , , . , — , , .

:

 #   eta = 0.001 epochs = 50 

:

 #    eta = 0.01 epochs = 8 

.

$$$\eta$ . , , .

, .

:

• : , , ( ). , , , , .
• : .

, ( ) $$$w$ , , . , , , . , , .

,

, .

, :

— :

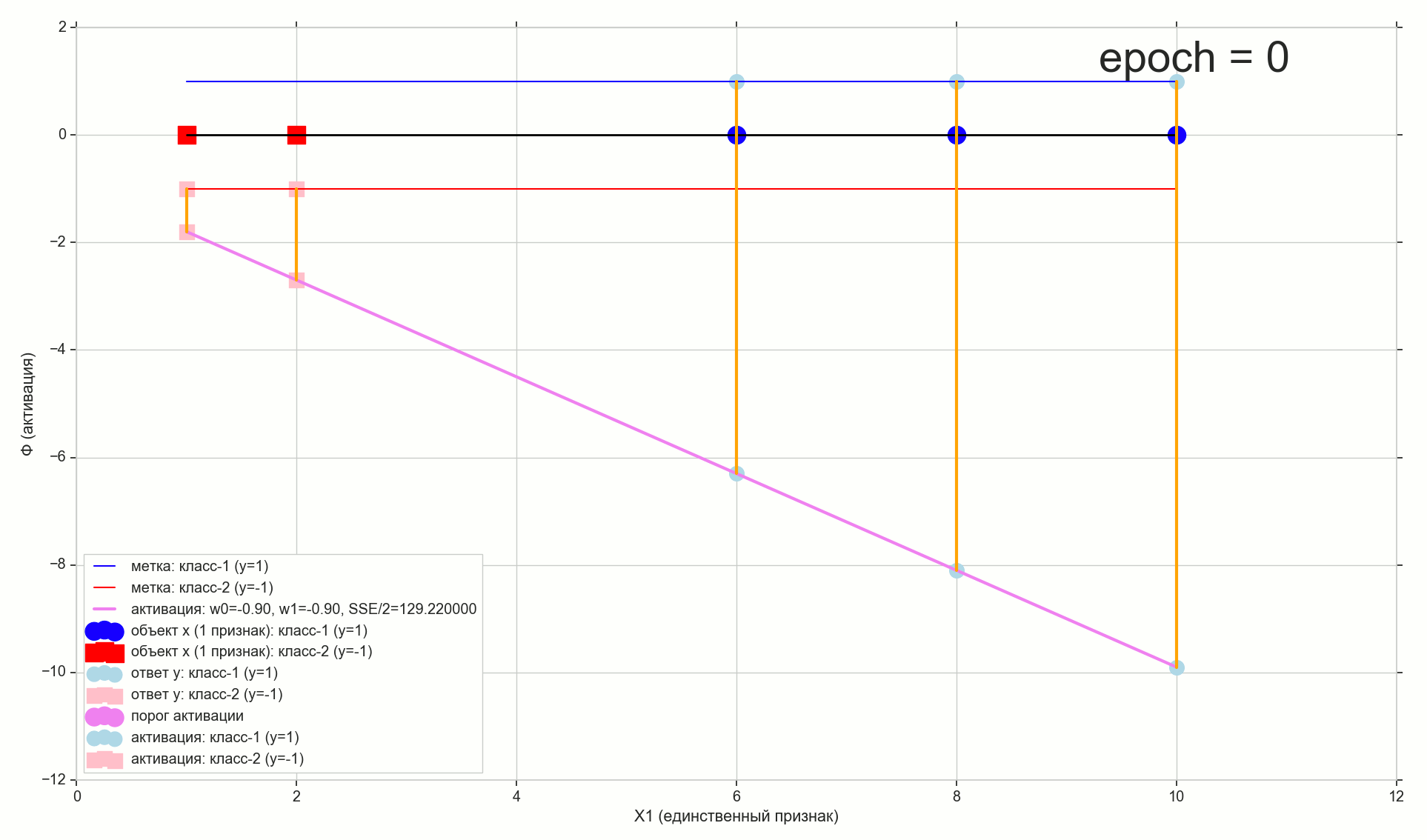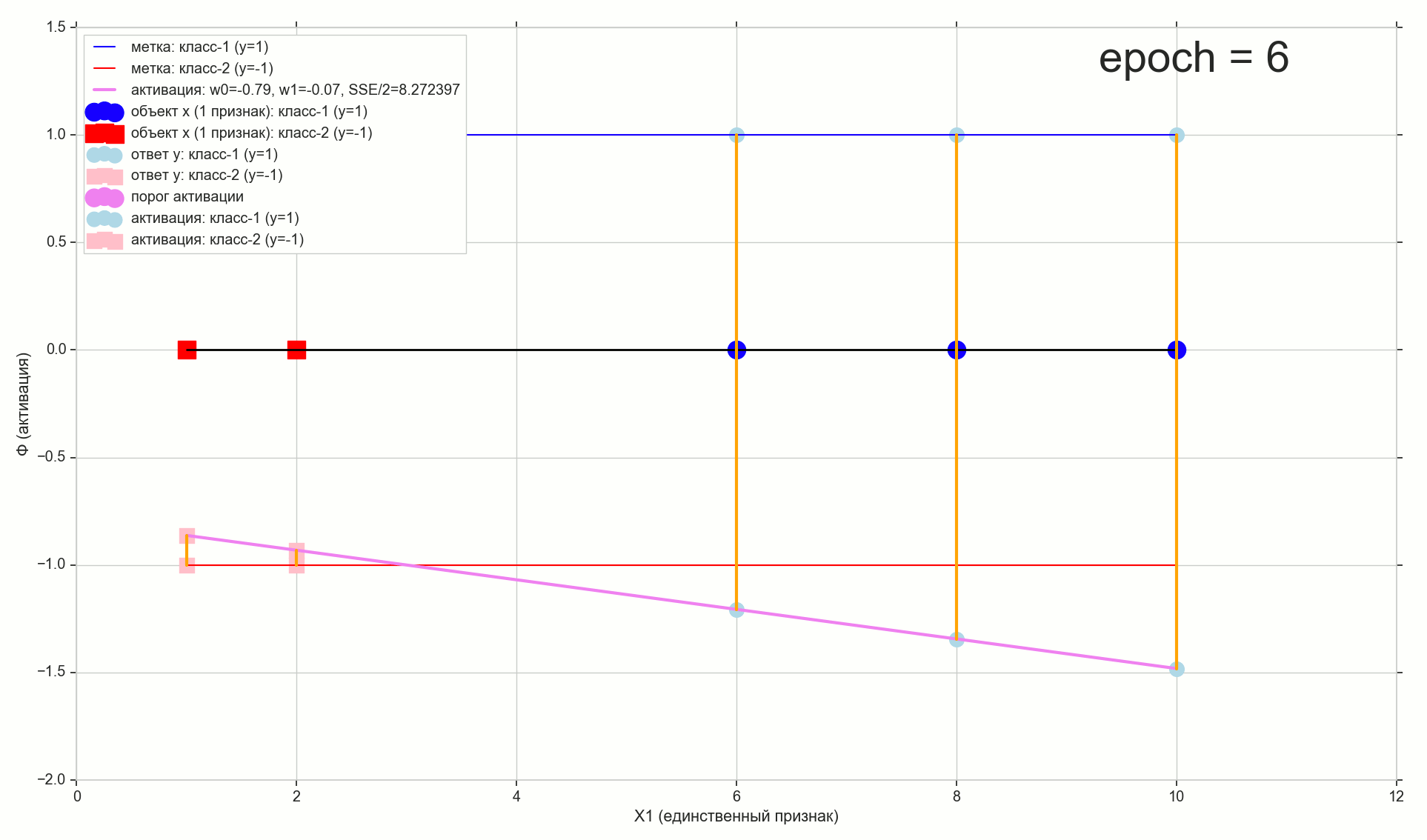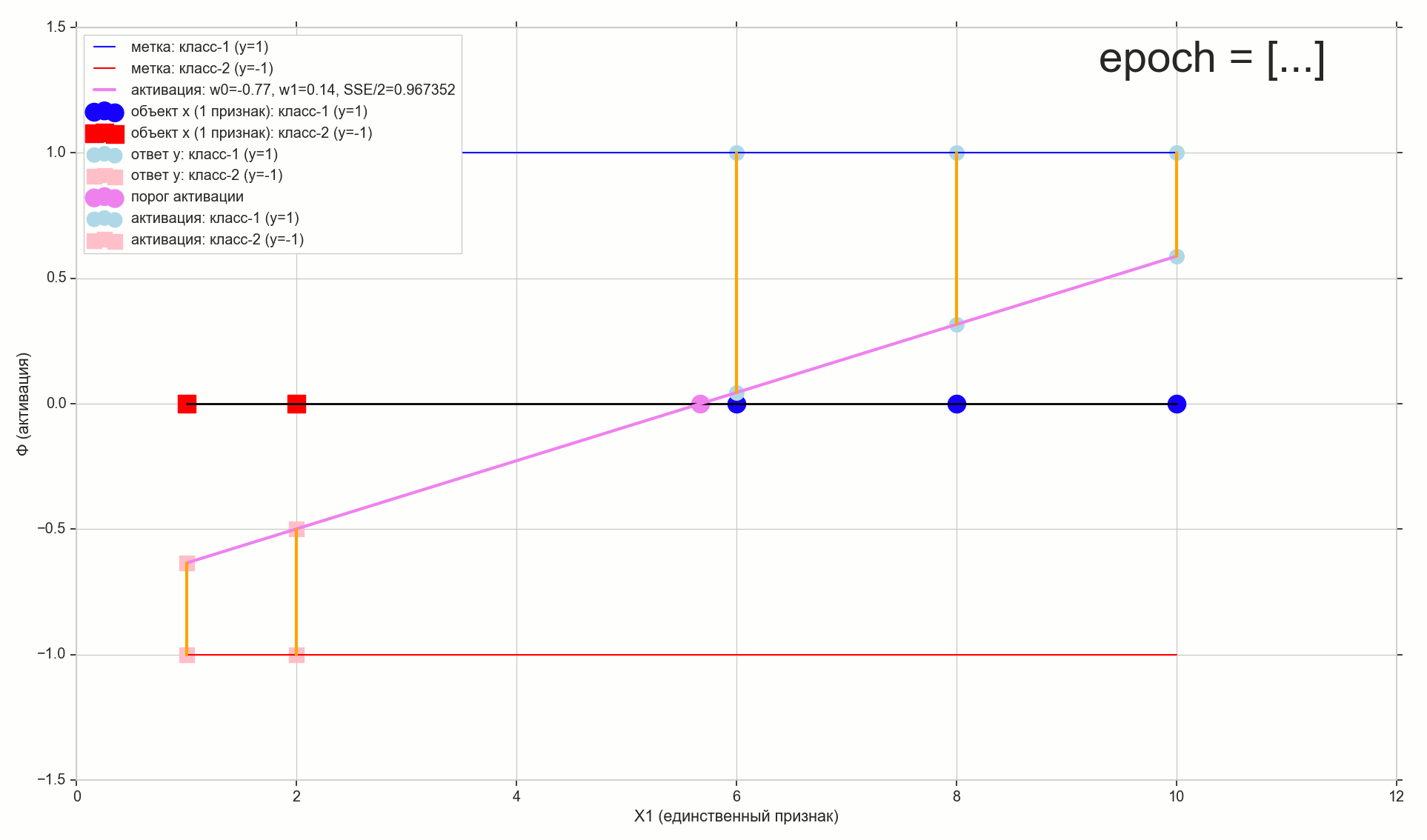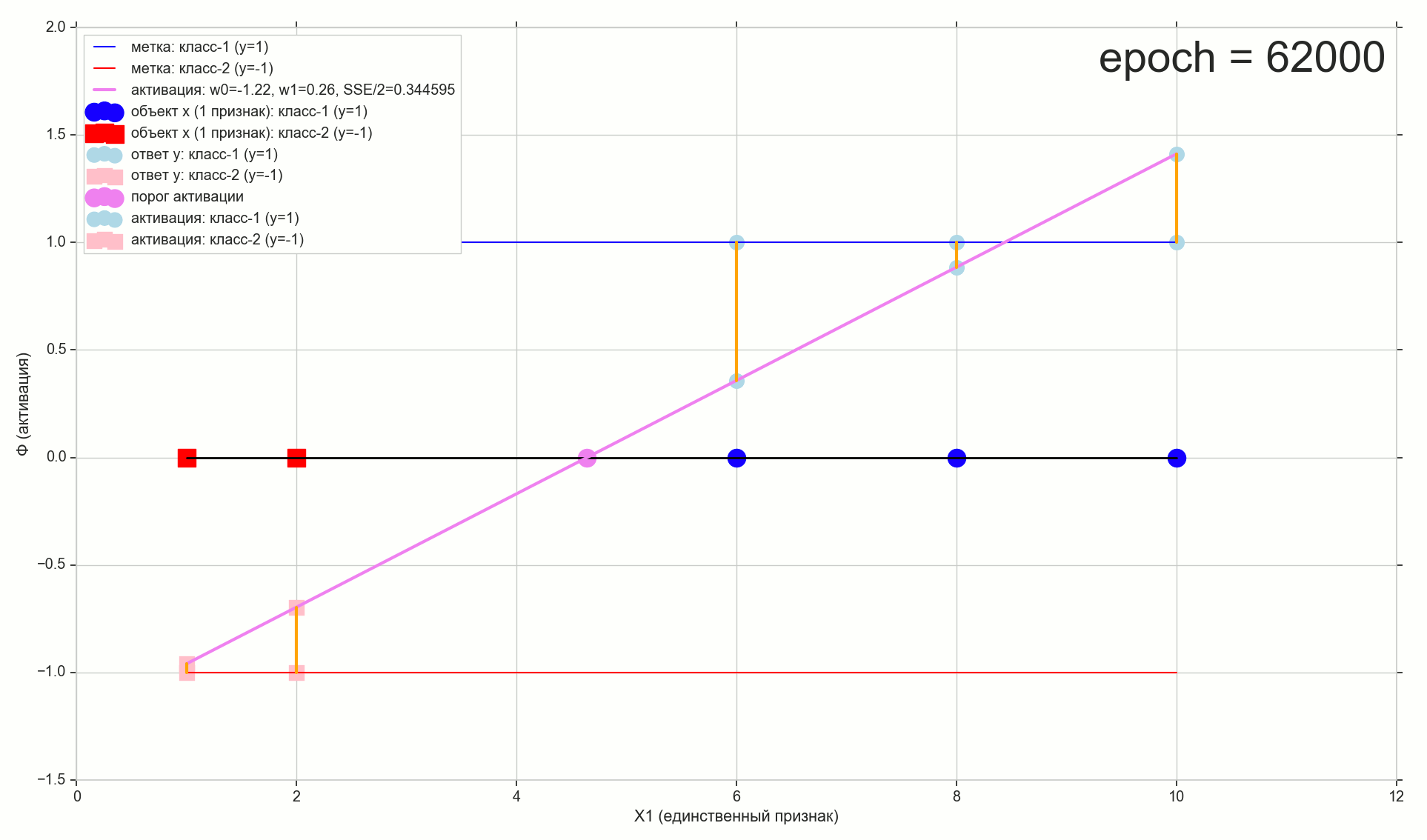
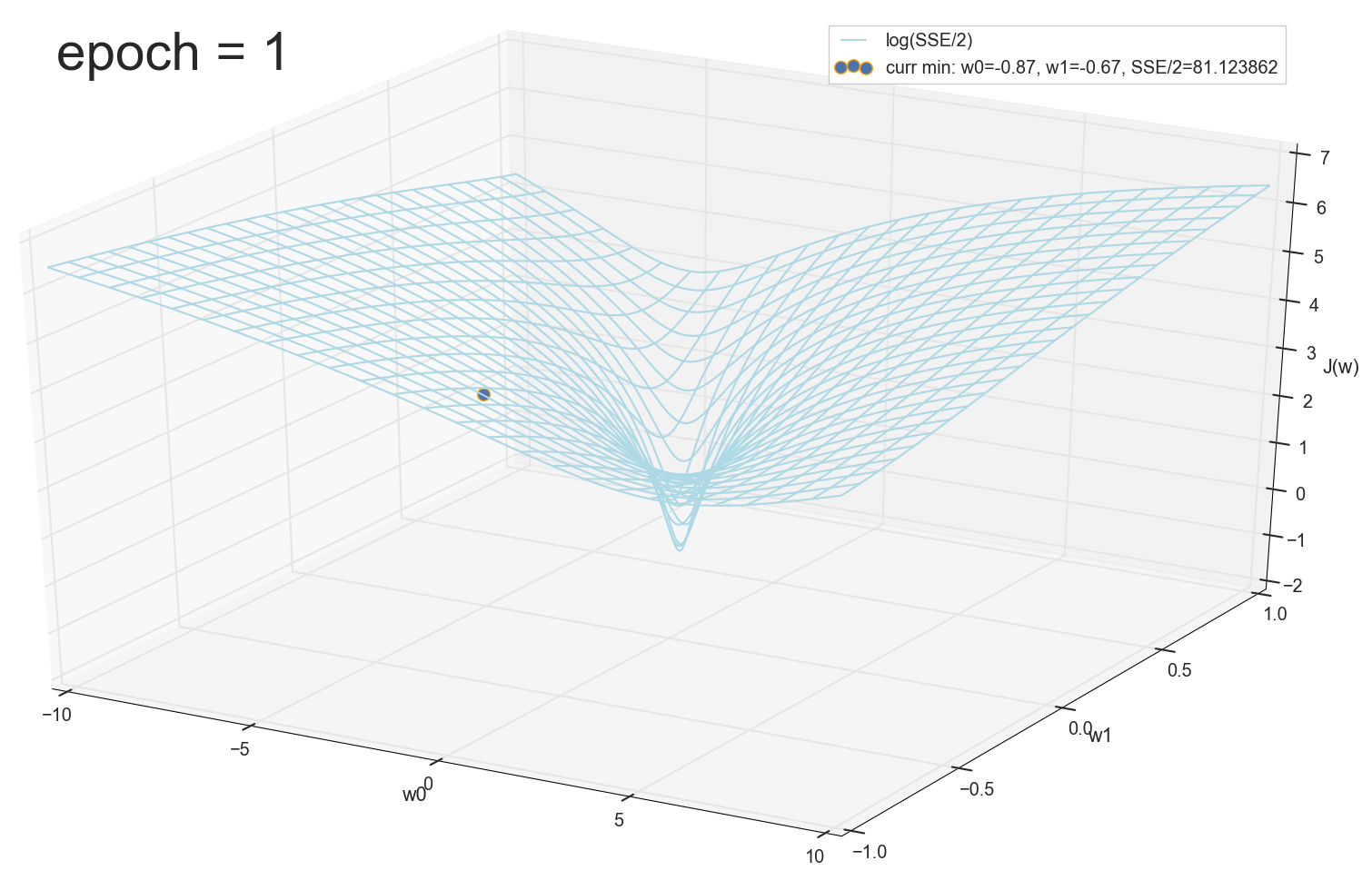
12 — , :

50 :

1767 — , :

, 62000 :

:

. , : , , . , , , , , , . , , - .

, , - , - : , , , , , — . , , , , , , , — . ?

, . :

, , ( ). : , . , , .

. , .

. , , . , — .

— :

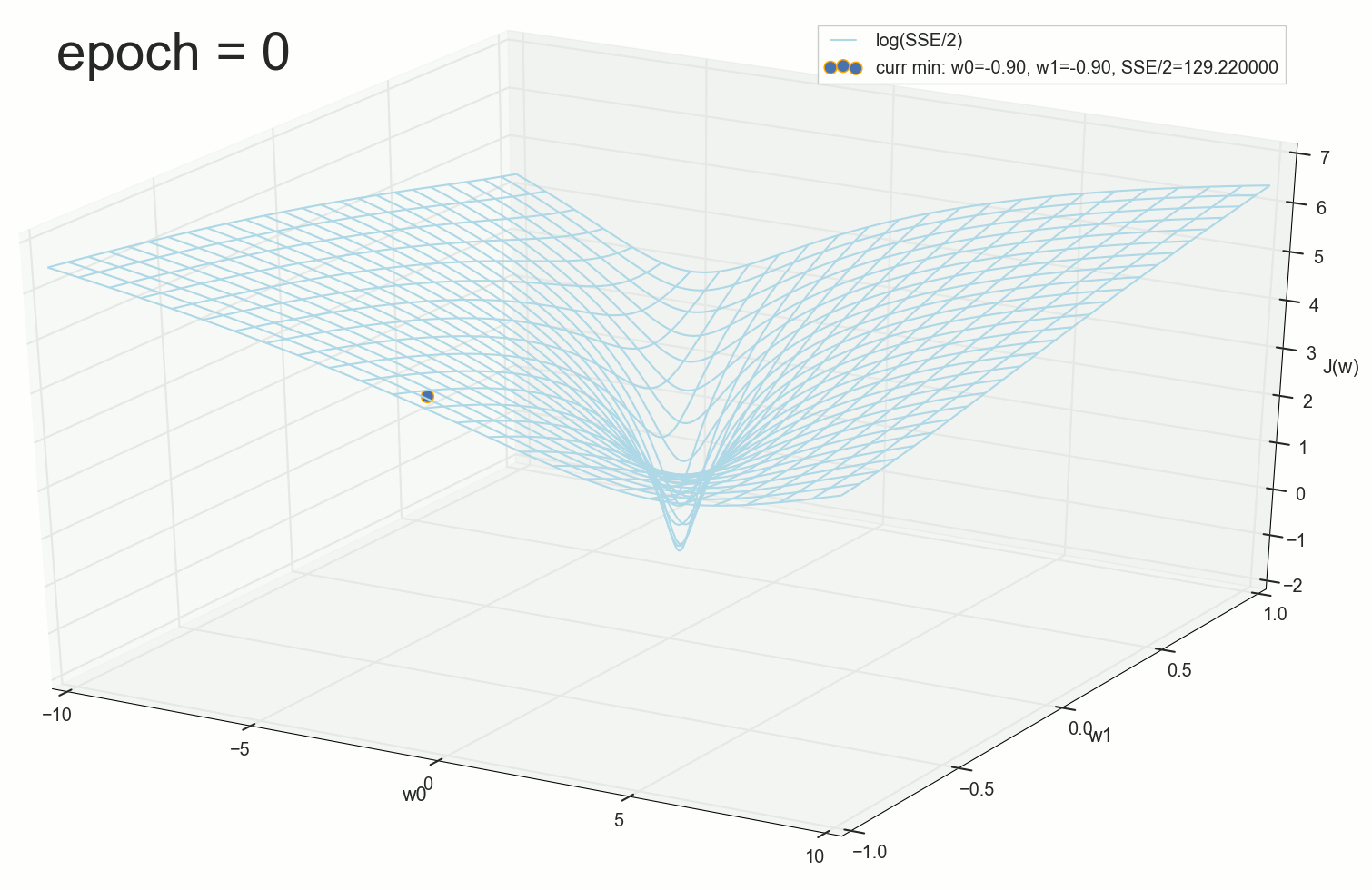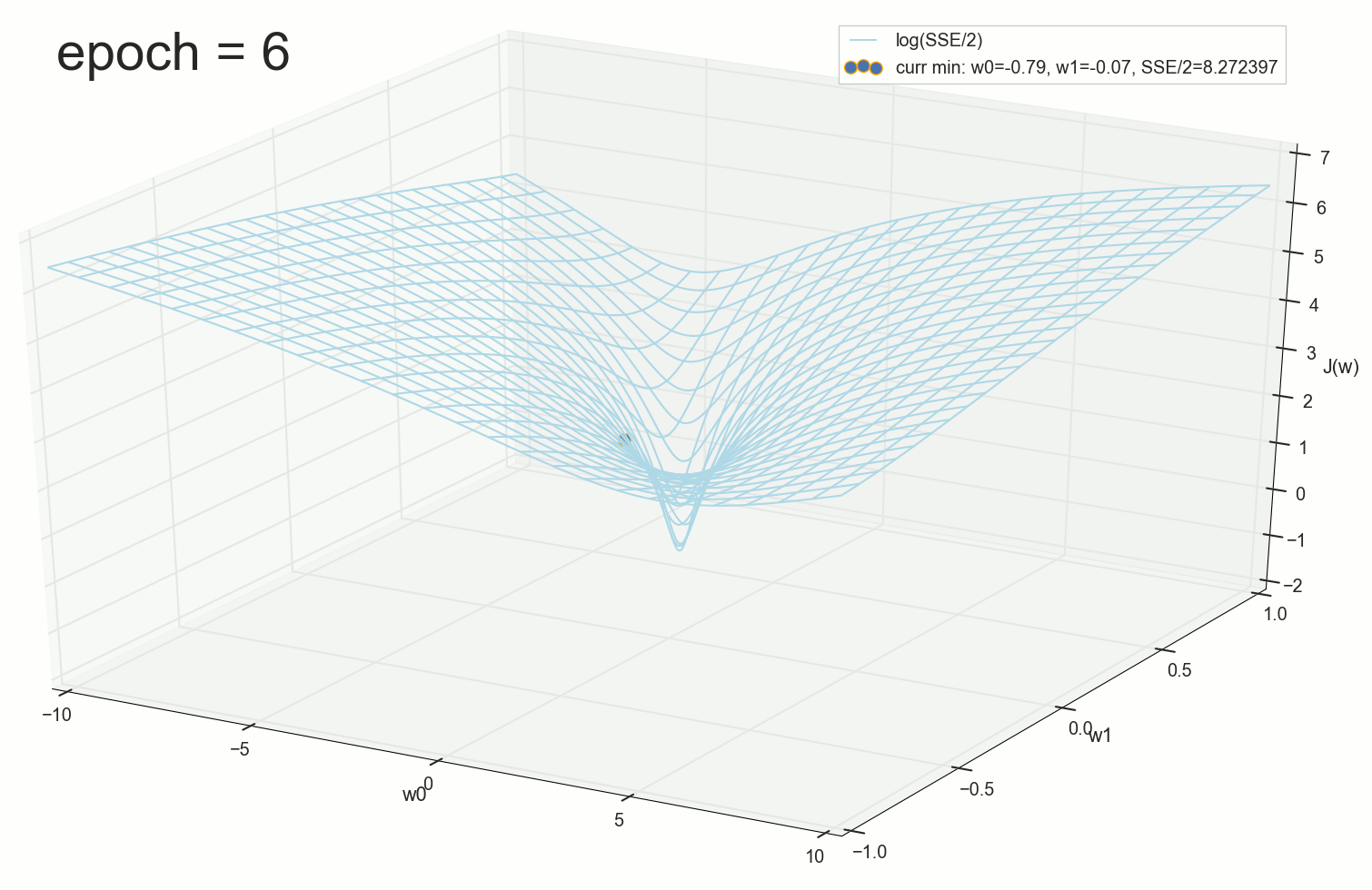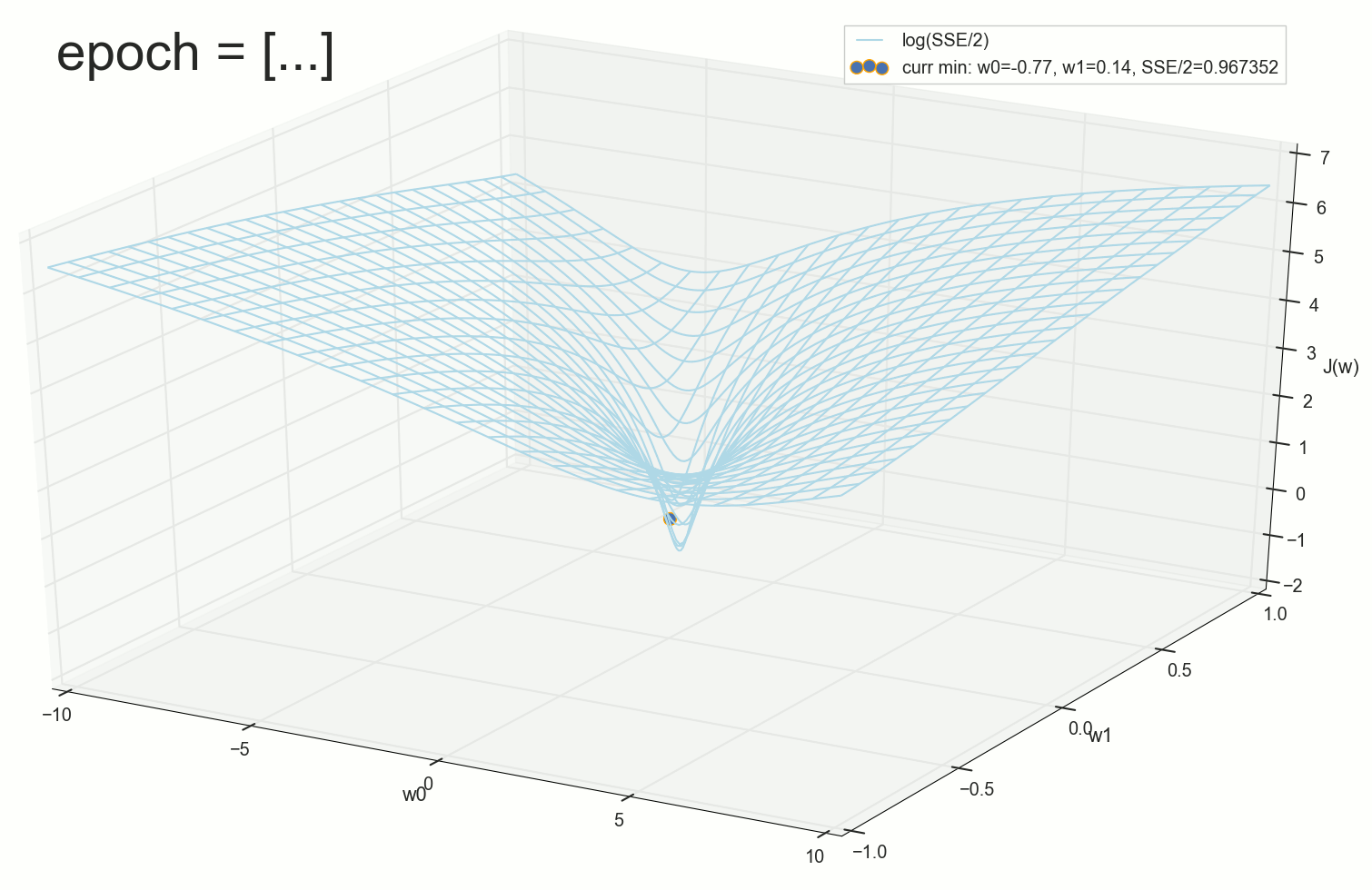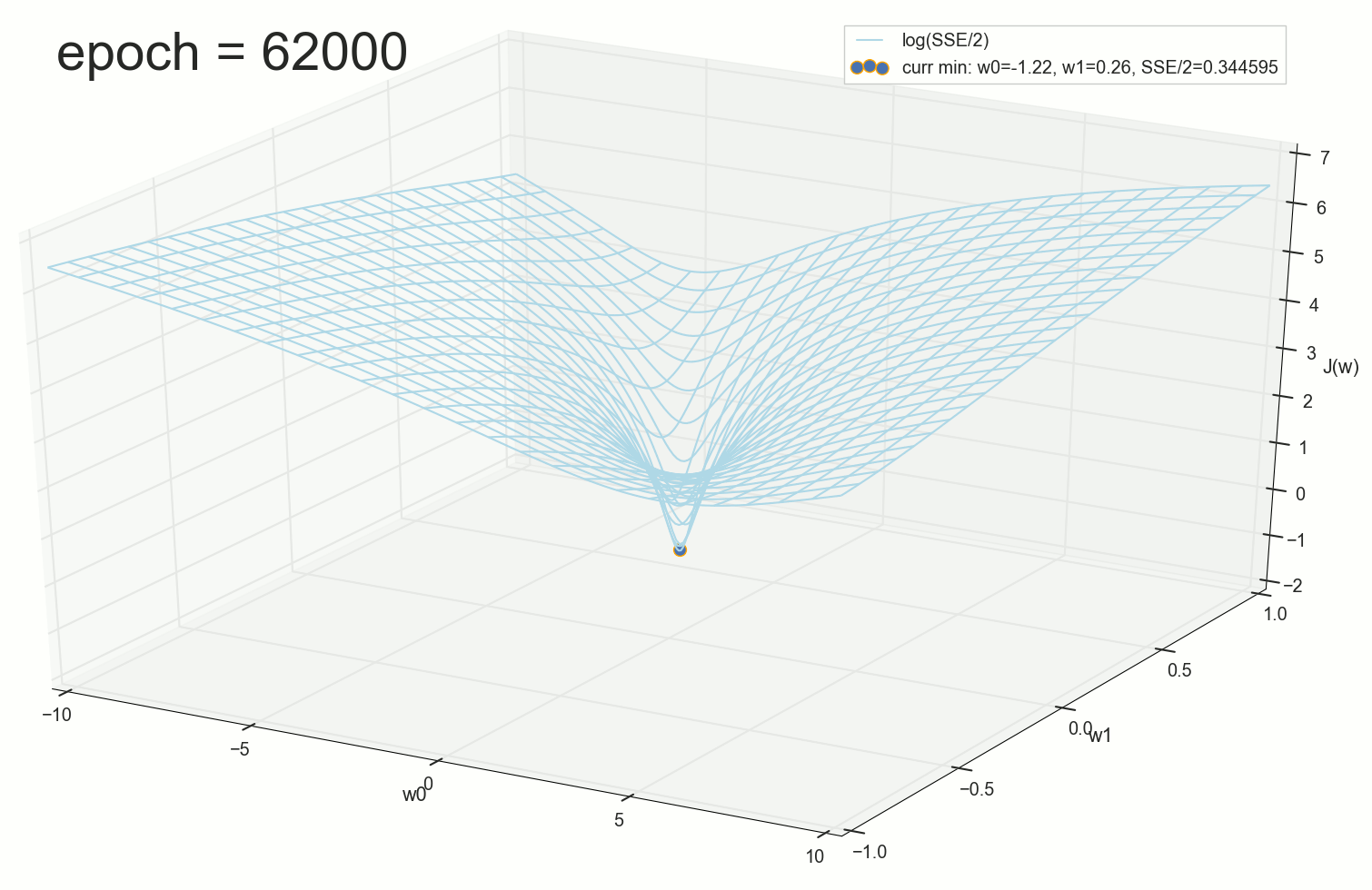
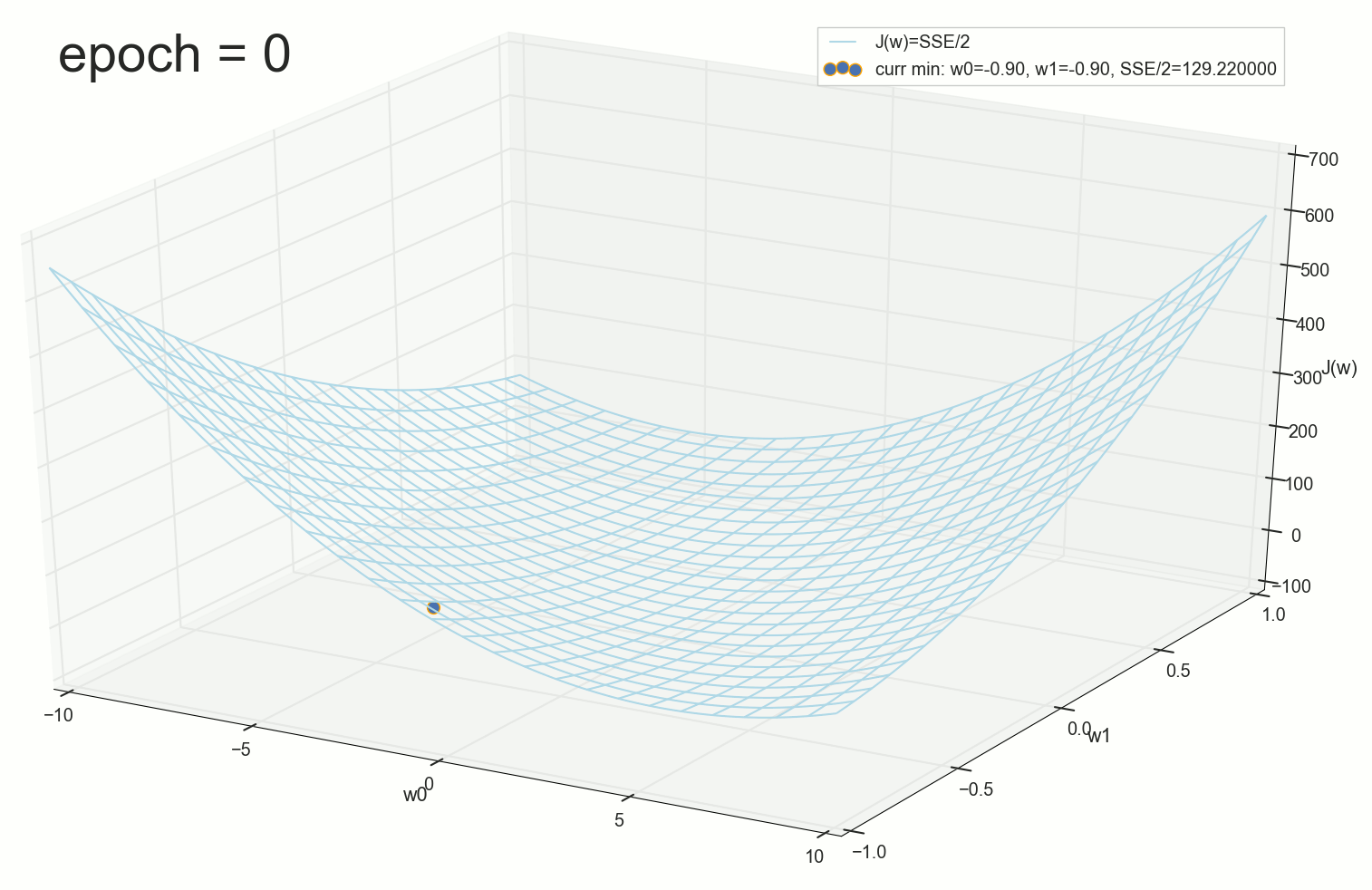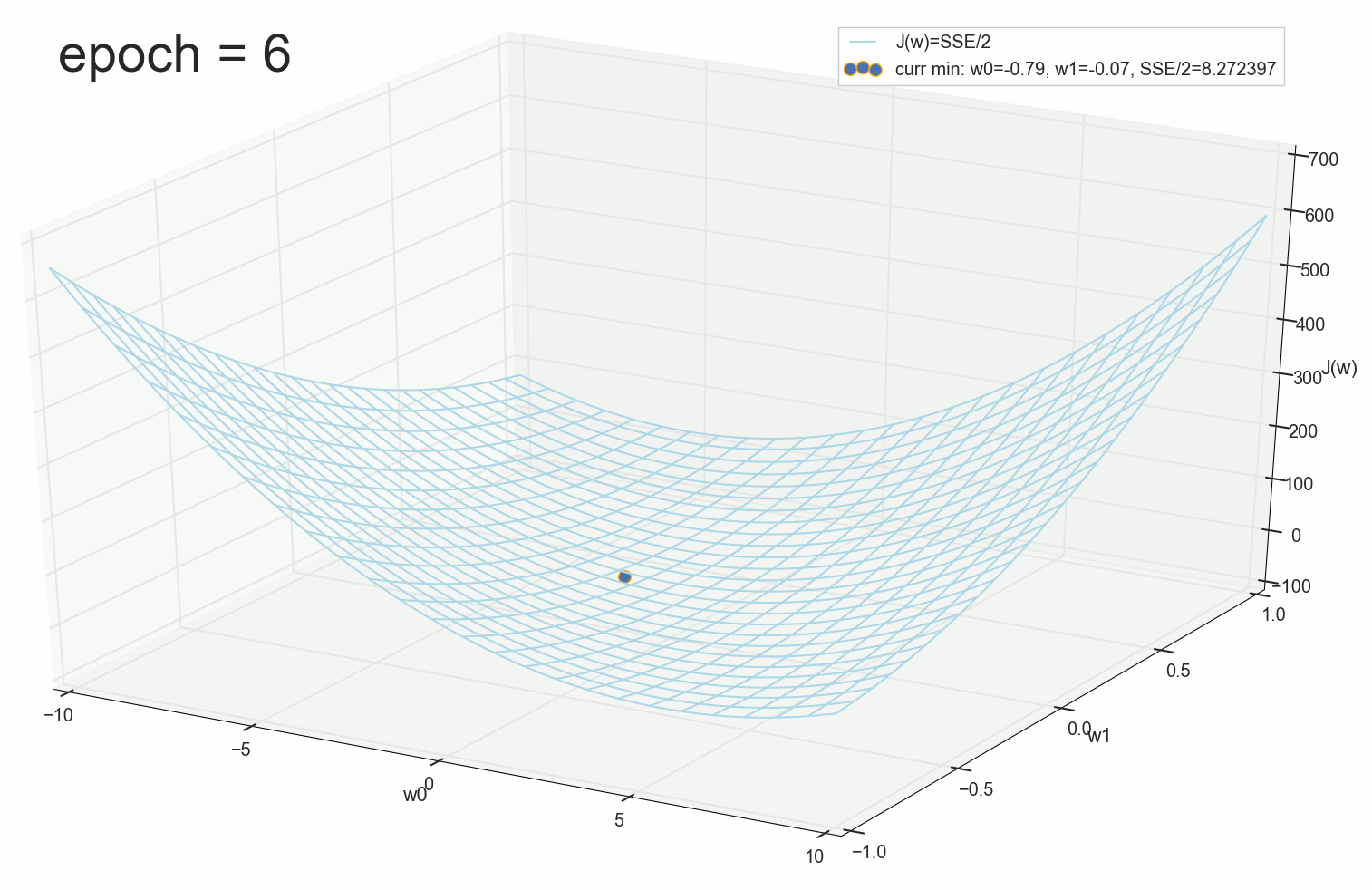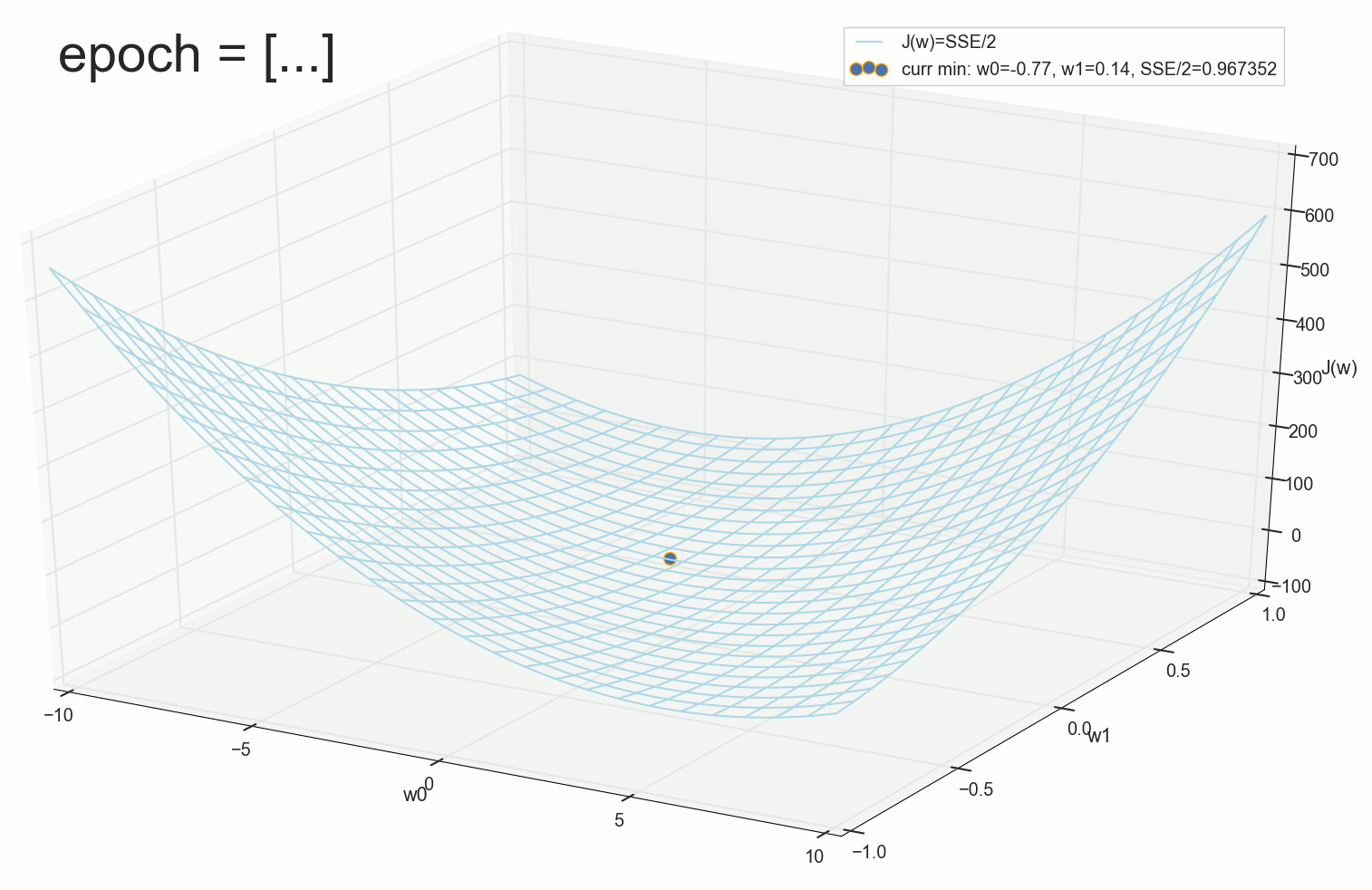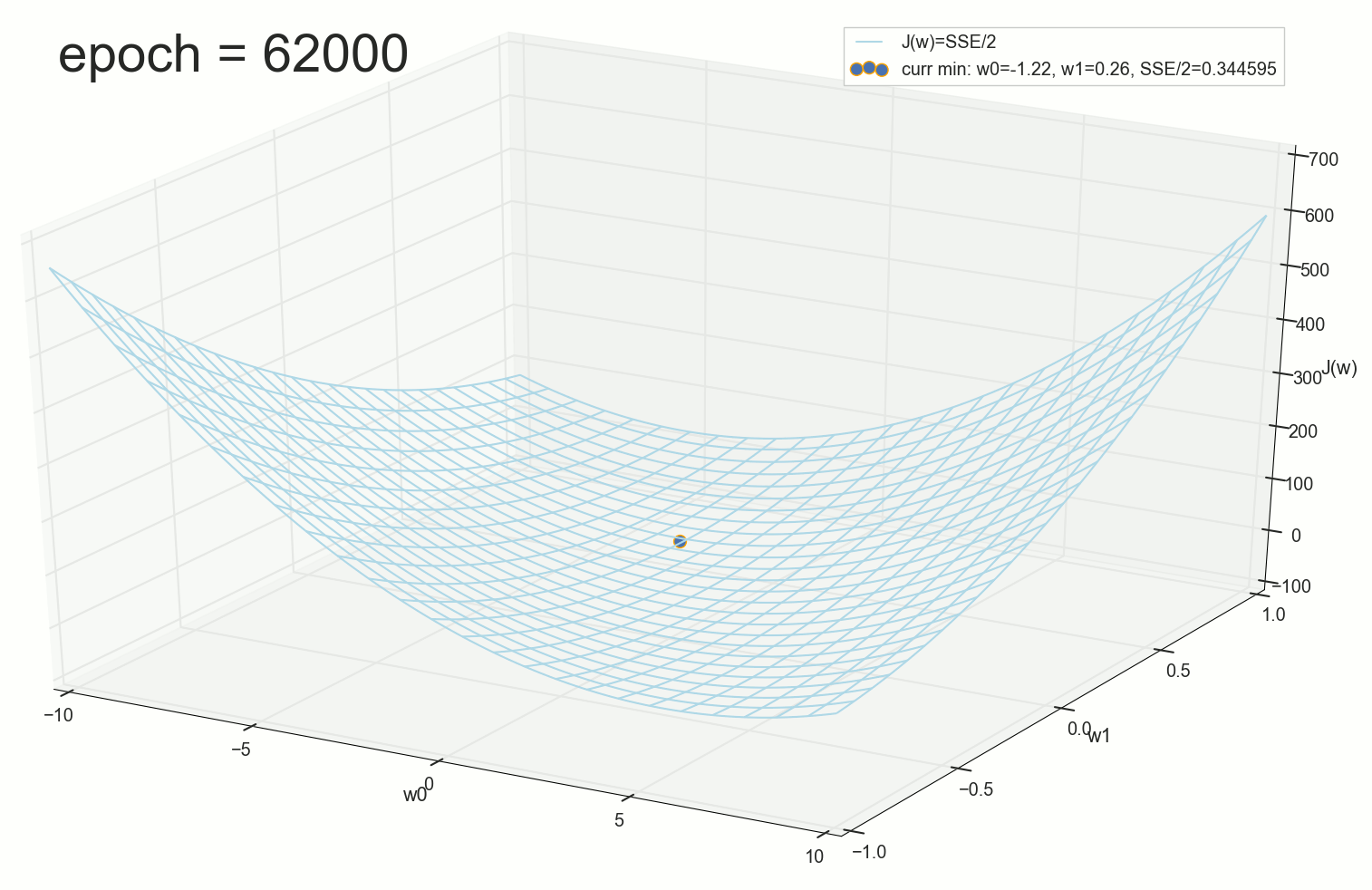
11- : , ; :

12- : , , :

50- : , 12-

1766: . $$$J(w)=0.3456480221$ — , , ( $$$J(w)=0.3456478372$ : 6- , , )

1767: $$$J(w)=0.34564503$ — , ( 6- , ). $$$w_0=-1.184831$ , $$$w_1=0.258455$ ( $$$w_0$ 2- : $$$w_0=-1.27$ , $$$w_1=0.26$ )

62000: $$$J(w)=0.3445945$ — , ( 2- ). :

:

. , , , , .

• $$$\eta=0.001$ , 10-12- ( )
• , , , (1767)
• — 60
• —

— ( , 1767): $$$w_0=-1.184831$ , $$$w_1=0.258455$ .

.

$$$t^{(1)}=(t_1^{(1)})=(1.4)$ ( , $$$t^{(i)}$ — ). , .. , , $$$\hat y=-1$ , .. .

$$ $$SUM=w_0 + w_1*t_1^{(1)} = -1.18 + 0.26*1.4=-0.816$$

$$ $$\Phi(SUM)=SUM=-0.816$$

$$ $$\Phi(SUM)=-0.816 < 0 \implies \hat y = -1$$

, .

: $$$t^{(2)}=(t_1^{(2)})=(7)$

$$ $$\Phi(SUM)=SUM= -1.18 + 0.26*7 = 0.64 \geqslant 0 \implies \hat y = 1$$

$$$\hat y = 1$, .. . .

, ( «» ) 12 . , !

(m=2)

, , , . . , , .

— ( ). 2- .

• $$$x = (x_1, x_2)$( , , )
• $$$y = \{-1, 1\}$( , )

 #  -  ( ) X1 = np.array([2, 3, 1, 5, 10, 1, 6, 7, 10, 6, 7]) X2 = np.array([1, 1, 2, 2, 3, 5, 6, 6, 7, 8, 8]) #   -   y = np.array([-1, -1, -1, -1, 1, -1, 1, 1, 1, 1, 1]) 

 plt.scatter(X1[y == -1], X2[y == -1], s=400, c='red', marker='*', label=u': -1') plt.scatter(X1[y == 1], X2[y == 1], s=200, c='blue', marker='s', label=u': 1') #    #  - -  w0 = -2.7 w1 = .3 w2 = .4 #   ( ) -      =0: # 0=w0+w1*X1+w2*X2 # X2=-(w0+w1*X1)/w2 plt.plot(np.linspace(0,12), -(w0+w1*np.linspace(0,12))/w2, label=u' ') plt.xlim(0, 11) plt.ylim(0, 9) plt.legend(loc='upper left') plt.xlabel('X1') plt.ylabel('X2') plt.show() 

, .

$$ $$\Phi(x, w) = w_0 + w_1 x_1 + w_2 x_2$$

, — , , 1- , 3-:

:

:

— :

() $$$\Phi(w) = 0$(-). :

, , , , , ( , ). , . , , m=2, (m+1)=3: , — , , — , ( ).

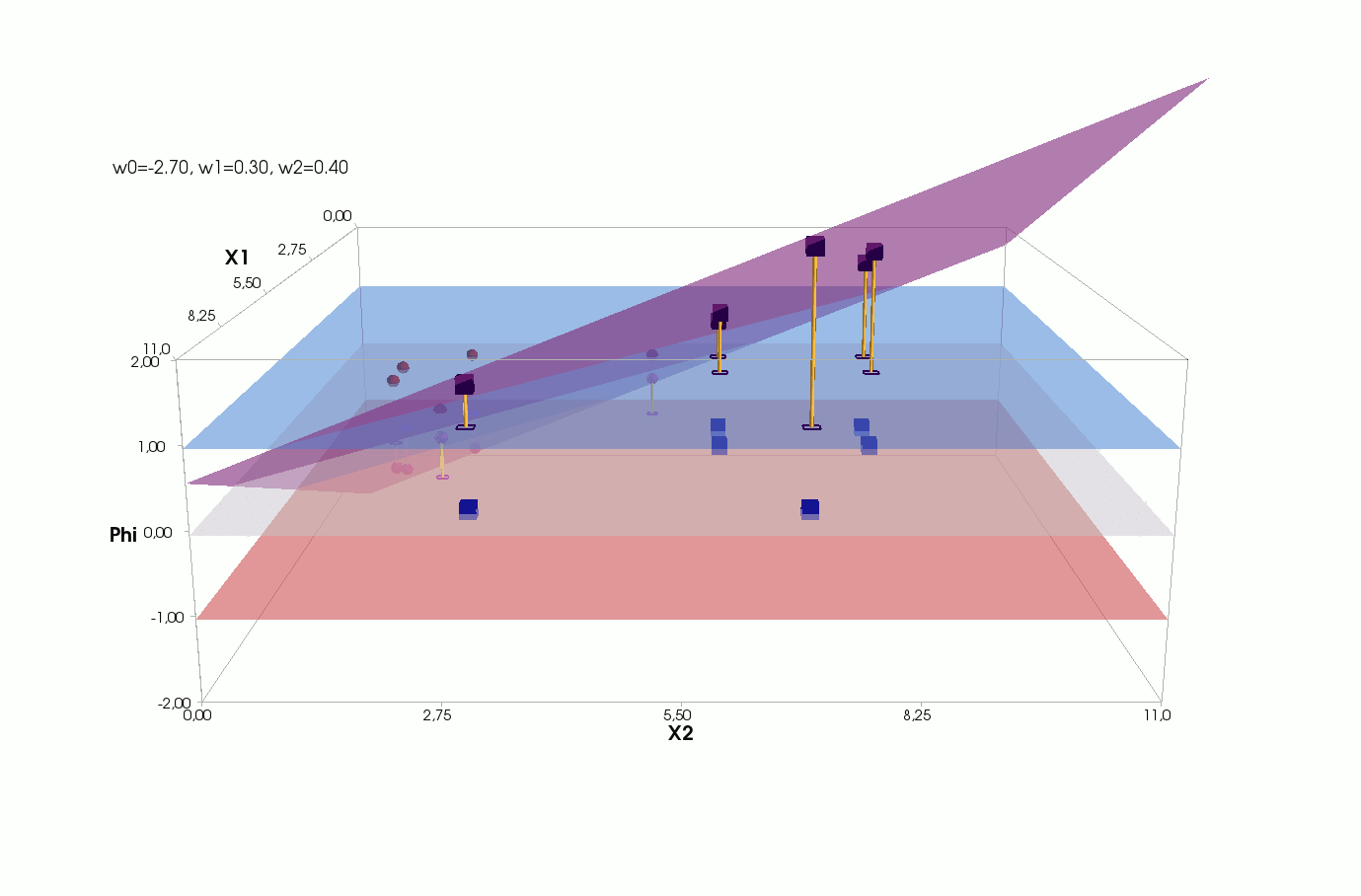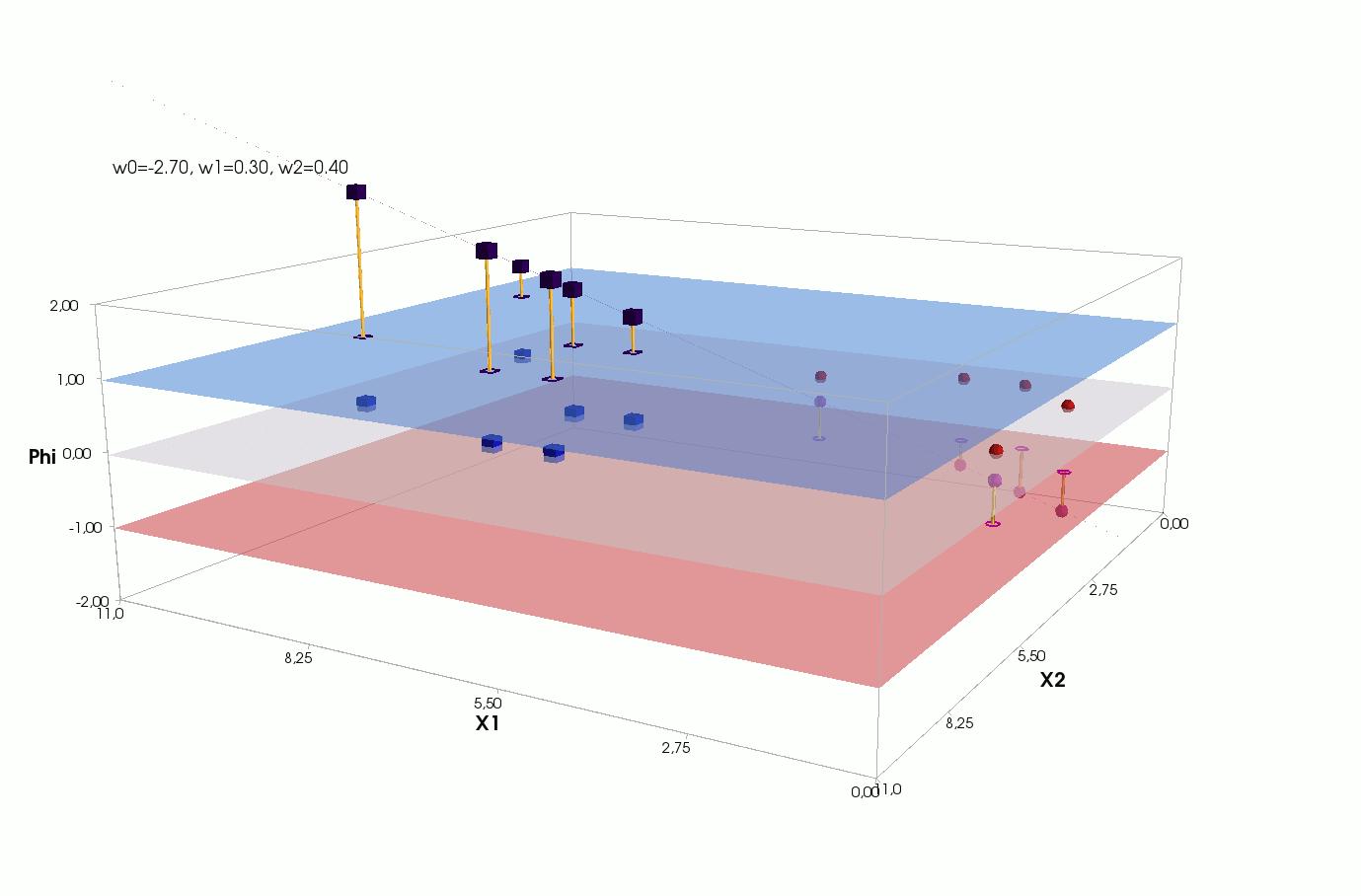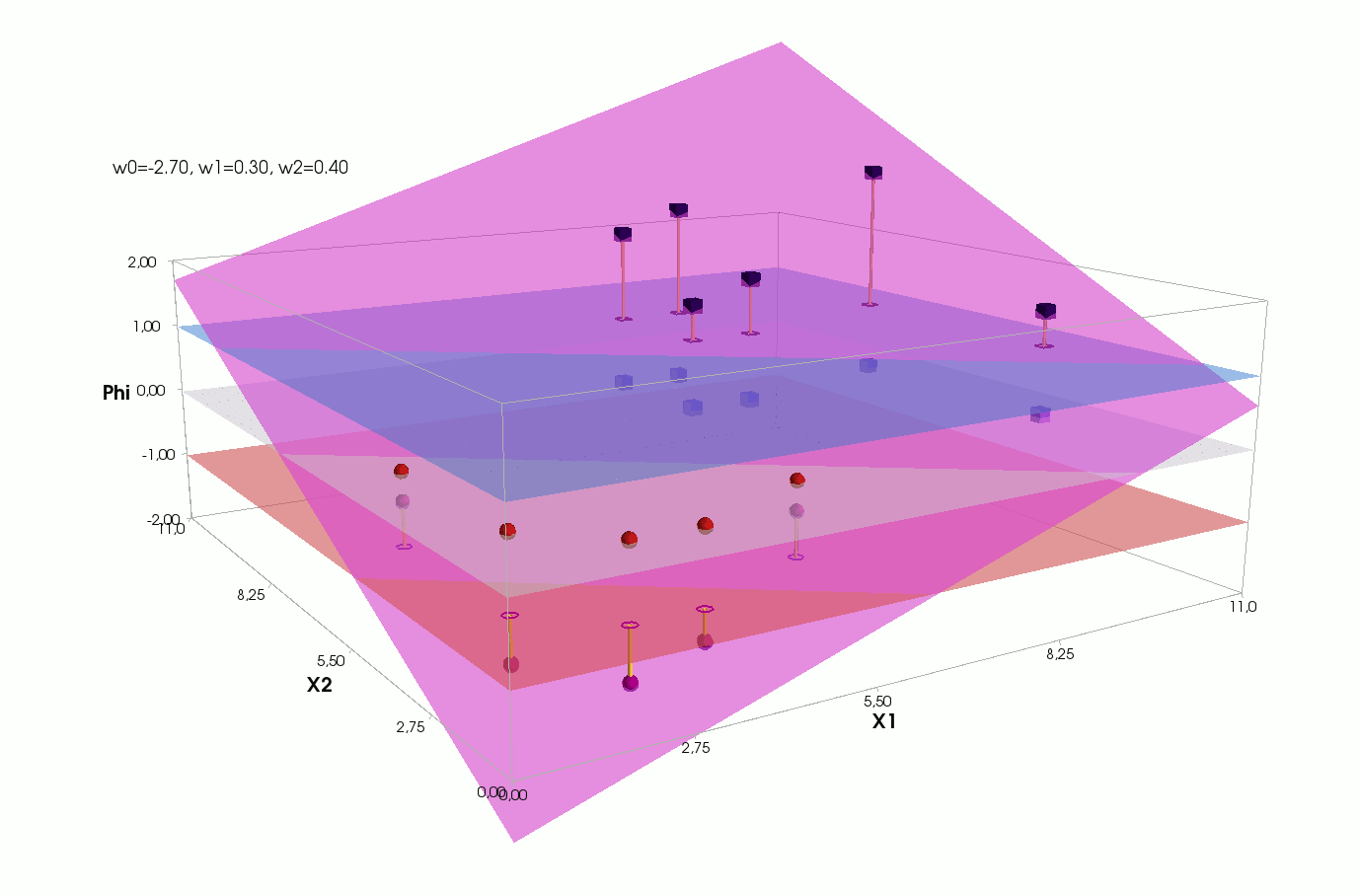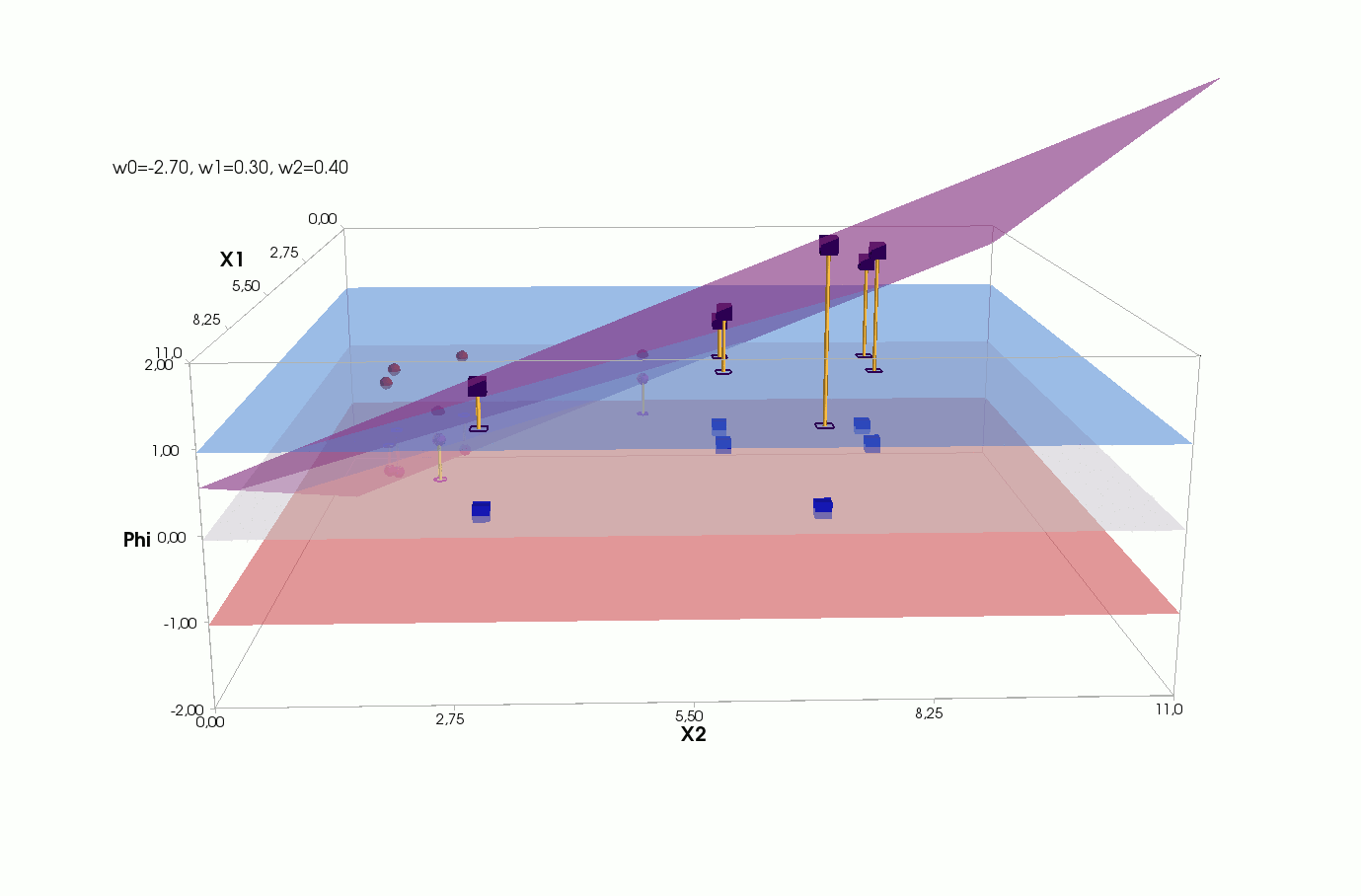
Erreur

$$ $$J(w)={1 \over 2} SSE = {1 \over 2}\sum_{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)} + w_{2}x_{2}^{(i)} - y^{(i)})^{2}$$

() , .., , 3 + — 4 . , 2- 3- - 3-, , - 4- 3-, .

2- . , , 1- 2-.

$$ $$\nabla J(w)=(\frac{\partial J(w)}{\partial w_{0}}, \frac{\partial J(w)}{\partial w_{1}}, \frac{\partial J(w)}{\partial w_{1}}), w=(w_{0}, w_{1}, w_{2})$$

( ):

$$ $$\frac{\partial J(w)}{\partial w_{0}} =\sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})$$

$$ $$\frac{\partial J(w)}{\partial w_{1}}= \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})x_{1}^{(i)}$$

$$ $$\frac{\partial J(w)}{\partial w_{2}}= \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})x_{2}^{(i)}$$

:

$$ $$\Delta w_{0}=-\eta \frac{\partial J(w)}{\partial w_{0}} =-\eta \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})$$

$$ $$\Delta w_{1}=-\eta \frac{\partial J(w)}{\partial w_{1}} =-\eta \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})x_{1}^{(i)}$$

$$ $$\Delta w_{2}=-\eta \frac{\partial J(w)}{\partial w_{2}} =-\eta \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})x_{2}^{(i)}$$

3- ( 3- ), $$$\eta=0.001$, $$$w_0=-0.9$, $$$w_1=-0.9$, $$$w_2=-0.9$.

— , , :

:

:

3- - :

4- :

60- — , :

70- , , :

200- — :

400- — :

:

, , $$$w_0$.

Code

matplotlib ( mpl_toolkits.mplot3d.axis3d) ( , , 3). Mayavi .

 import numpy from mayavi import mlab #    -   mlab.savefig #mlab.options.offscreen = True #   size    mlab.savefig fig = mlab.figure(fgcolor=(10./256., 10./256., 10./256.), bgcolor=(255./256., 255./256., 255./256.), size=(1650, 950)) X1_ = range(0, 12) X2_ = range(0, 12) XX1_, XX2_ = np.mgrid[X1_, X2_] #    # : color=(255./256., 191./256., 71./256.) # : color=(171./256., 0./256., 130./256.) # : color=(255./256., 101./256., 107./256.) # : color=(252./256., 79./256., 245./256.) # : color=(84./256., 148./256., 247./256.) # : color=(45./256., 0./256., 82./256.) # : color=(254./256., 255./256., 87./256.) #  # : color=(.7, .1, .1) # : color=(.1, .1, .7) #   : =1 (y=1), =-1 (y=-1)    =0 mlab.surf(XX1_, XX2_, np.full((12, 12), -1), color=(255./256., 101./256., 107./256.), opacity=0.6) mlab.surf(XX1_, XX2_, np.full((12, 12), 1), color=(84./256., 148./256., 247./256.), opacity=0.5) mlab.surf(XX1_, XX2_, np.full((12, 12), 0), color=(247./256., 243./256., 246./256.), opacity=0.5) #     # (   , ..      ,   #     :    2- , 3  - #   ,   ) mlab.points3d(X1[y == -1], X2[y == -1], np.full(X1[y == -1].size, 0), color=(.7, .1, .1), mode='sphere', scale_factor=.2) mlab.points3d(X1[y == 1], X2[y == 1], np.full(X1[y == 1].size, 0), color=(.1, .1, .7), mode='cube', scale_factor=.2) #     mlab.points3d(X1[y == -1], X2[y == -1], np.full(X1[y == -1].size, -1), color=(171./256., 0./256., 130./256.), mode='2dcircle', scale_factor=.2) mlab.points3d(X1[y == 1], X2[y == 1], np.full(X1[y == 1].size, 1), color=(45./256., 0./256., 82./256.), mode='2dsquare', scale_factor=.2) #    #      # ... epoch=12 w0=-0.762718 w1=0.165023 w2=0.040271 sse=3.598883 #  -   y=w0+w1*X1+w2*X2 yy_ = w0 + w1*XX1_ + w2*XX2_ actsurf = mlab.surf(XX1_, XX2_, yy_, color=(252./256., 79./256., 245./256.), opacity = 0.6) #       y_ = w0 + w1*X1 + w2*X2 mlab.points3d(X1[y==-1], X2[y==-1], y_[y==-1], color=(171./256., 0./256., 130./256.), mode='sphere', scale_factor=.2) mlab.points3d(X1[y==1], X2[y==1], y_[y==1], color=(45./256., 0./256., 82./256.), mode='cube', scale_factor=.2) #   -       #      for i in range(len(X1[y==-1])): mlab.plot3d( [X1[y==-1][i], X1[y==-1][i]], [X2[y==-1][i], X2[y==-1][i]], [y[y==-1][i], y_[y==-1][i]], color=(255./256., 191./256., 71./256.)) for i in range(len(X1[y==1])): mlab.plot3d( [X1[y==1][i], X1[y==1][i]], [X2[y==1][i], X2[y==1][i]], [y[y==1][i], y_[y==1][i]], color=(255./256., 191./256., 71./256.)) #   -       # (      ) zmin=-2. zmax=2. vis_area = mlab.points3d( [np.min(X1_), np.max(X1_)], [np.min(X2_), np.max(X2_)], [zmin, zmax], mode='point') #          mlab.view( focalpoint=((np.max(X1_)-np.min(X1_))/2, (np.max(X2_)-np.min(X2_))/2, (zmax-zmin)/2), distance=25, azimuth=-50, elevation=75) mlab.move((0,0,10)) #           fig.scene.renderer.use_depth_peeling = 1 #  mlab.outline(vis_area, color=(.7, .7, .7)) #   ,      : -2, -1, 0, 1, 2 axes = mlab.axes(vis_area, nb_labels=5, color=(.7, .7, .7), ranges=[np.min(X1_), np.max(X1_), np.min(X2_), np.max(X2_), zmin, zmax], #xlabel=u'X1', ylabel=u'X2', zlabel=u'(SUM) - ') xlabel=u'X1', ylabel=u'X2', zlabel=u'Phi') #      #from pprint import pprint #pprint(vars(axes)) axes._label_text_property.bold = False axes._label_text_property.italic = False axes._title_text_property.bold = True axes._title_text_property.italic = False #  ,     #axes._title_text_property.font_size = 34 #         : axes.axes.font_factor = .7 #       size  mlab.figure, #        title = mlab.title("epoch=" + str(epoch)) title.actor.text_scale_mode='none' title.property.justification='right' title.property.font_size=48 legend = mlab.text(.6, .8, 'w0=%0.2f, w1=%0.2f, w2=%0.2f, sse/2=%0.6f'%(w0, w1, w2, sse/2)) legend.actor.text_scale_mode='none' legend.property.font_size=18 #   mlab.show() #    #mlab.savefig("epoch" + str(epoch) + ".png") #    :     ,    # (    , , ,  , #    ,     ) #mlab.clf() #mlab.close() #    -      ''' fpoint = ( (np.max(X1_)-np.min(X1_))/2, (np.max(X2_)-np.min(X2_))/2, (zmax-zmin)/2 ) for i in range (0, 360, 2): mlab.view(focalpoint=fpoint, distance=25, elevation=75, azimuth=i) mlab.move((0,0,10)) mlab.savefig("act-2d-azimuth" + str(i) + ".png") ''' 

, Mayavi , . , , , .

Mayavi, Matplotlib/axes3d, 3- OpenGL. , ( ) , Qt. mayavi . pip PyQt5 python-qt (, - , 'qt'). , , , , , :

 env QT_API=pyqt python3 gradient-2d.py 

— $$$J(w)$

 def sse_(X1, X2, y, w0, w1, w2): return ((w0+w1*X1+w2*X2 - y)**2).sum() #      J(w0, w1, w2) #   w0, w1  w2 #   eta = 0.001 #      () epochs = 70 w0_first = -.9 w1_first = -.9 w2_first = -.9 #      w0_epochs = [w0_first] w1_epochs = [w1_first] w2_epochs = [w2_first] delta_w0_epochs = [] delta_w1_epochs = [] delta_w2_epochs = [] w0_next = w0_first w1_next = w1_first w2_next = w2_first for i in range(epochs): grad_w0 = (w0_next + w1_next*X1 + w2_next*X2 - y).sum() delta_w0 = -eta*grad_w0 grad_w1 = ((w0_next + w1_next*X1 + w2_next*X2 - y)*X1).sum() delta_w1 = -eta*grad_w1 grad_w2 = ((w0_next + w1_next*X1 + w2_next*X2 - y)*X2).sum() delta_w2 = -eta*grad_w2 w0_next = w0_next + delta_w0 w1_next = w1_next + delta_w1 w2_next = w2_next + delta_w2 delta_w0_epochs.append(delta_w0) delta_w1_epochs.append(delta_w1) delta_w2_epochs.append(delta_w2) w0_epochs.append(w0_next) w1_epochs.append(w1_next) w2_epochs.append(w2_next) #     sse_epochs = [] for i in range(len(w1_epochs)): sse = sse_(X1, X2, y, w0_epochs[i], w1_epochs[i], w2_epochs[i]) sse_epochs.append(sse) #print('epoch=%d, w0=%f, w1=%f, w2=%f, SSE=%f, SSE/2=%f' % # (i, w0_epochs[i], w1_epochs[i], w2_epochs[i], sse, sse/2)) sse_epochs = np.array(sse_epochs) #  -      η (--) plt.plot(range(len(sse_epochs)), sse_epochs, label=u'J(w)=SSE/2, η=%s'%eta) plt.xlabel(u'epoch (η=%s)'%eta) plt.ylabel(u'J(w)') plt.legend(loc='upper right') plt.show() 

12 :

70 :

, , : 6-12- , 70- — 70- , 30-, 40- 200-, , , , .

Conclusion

ADALINE (adaptive linear neuron — ) — . scikit-learn ADALINE ( - , ) , , - « 80-» (ADALINE 60-), .

«Python » ( scikit-learn) , - .

ADALINE .

-, — , : , , , .

-, () , , , ( , , $$$y$) — , scikit-learn.

PS , ADALINE . , , , , ADALINE - , . , ADALINE . , - .