Juste la division, ou comment créer une théorie mathématique et y gagner 400 000 $. Deuxième série, avant-dernière

Dans la série précédente , nous avons examiné les nombres fractionnaires qui n'incluaient pas les nombres rationnels. Aujourd'hui, c'est précisément cette partie, non considérée, qui nous attend, et nous préparerons également une partie finale un peu plus compliquée sans utiliser de termes comme classes de résidus anneaux ou comparaisons modulo avec logarithme discret. Toujours dans la troisième partie des intéressés, des prix de 400 000 $ sont en attente. Pourquoi dans le troisième? Parce que sans introduction au sujet, il n'est pas toujours facile de comprendre les raisons pour lesquelles les prix ne sont pas si faciles à obtenir. Et après la lecture - seulement de la chance et une activité déterminée, patiente, mais pas très difficile, c'est tout ce dont vous avez besoin.

Étoiles rationnelles

Pour répondre aux questions posées précédemment sur les nombres rationnels, nous avons encore besoin d'une petite digression. Tout d'abord, rappelons que dans le processus de division par le «coin», nous obtenons constamment le reste de la division d'une certaine partie du nombre de dividendes par le diviseur. Dans ce cas, toute la partie de la division est écrite dans le résultat et le reste de la division est multiplié par la base du système numérique, après quoi la procédure de division avec le reste est répétée jusqu'à ce que la période soit détectée ou que tous les facteurs du diviseur soient réduits et que nous obtenions la fraction finale.

Cela ressemble à ceci:

5 | 3 ------ 1.66(6) 3 20 18 20 18 2 ... 

Ici, le reste de la soustraction de 18 à 20 est toujours égal à deux, que nous multiplions ensuite par la base du système de nombres décimaux.

Voyons maintenant en quoi la division de 5 par 3 diffère, par exemple, de la division de 1 par 3? La réponse est simple - la présence de la partie entière en conséquence. Mais nous nous sommes interrogés sur la période et la partie qui précède la période (appelée pré-période), mais qui n'est pas incluse dans toute la partie du résultat. Par conséquent, nous n'avons pas besoin de considérer l'ensemble de la partie. Par conséquent, dans cet exemple, tous les nombres supérieurs à 3 ou égaux peuvent être exclus de la prise en compte. Et ce qui est encore plus intéressant - les lois de la division se manifestent à bien des égards sans aucun autre nombre sauf un. Autrement dit, il suffit d'étudier la division d'une unité en une série d'entiers, de grandes unités, et nous comprendrons comment répondre à toutes les questions posées, et en même temps, nous rencontrerons un nombre très décent de nouvelles étoiles.

En attendant, nous n'avons pas commencé une étude sérieuse du sujet - quelques astuces. Savez-vous que le partage peut se faire «vice versa»? Pas comme nous sommes habitués à l'école, mais à partir de la fin. Montrons cela dans un autre exemple, dans lequel nous prenons le dernier reste et, à partir de celui-ci, nous calculons la période de fraction. Rappelons que le reste de la division de 5 par 3 était égal à 2. Quel a été le dernier nombre que nous avons soustrait pour obtenir une égalité? Nous n'avons pas besoin de nous souvenir, car nous savons que nous soustrayons toujours les nombres du reste précédent multiplié par 10, c'est-à-dire que le dernier chiffre de la décrémentation est toujours égal à 0. Cela signifie qu'il suffit de trier les produits du triple par des nombres de 1 à 9, = (3,6 , 9,12,15,18,21,24,27), pour voir - parmi eux, un seul se termine par 8 et, au total avec le reste 2, donne zéro dans le dernier chiffre du décrémenté. Donc, avant d'obtenir le reste de 2, nous avons soustrait 18 de 20. Pourquoi de 20? Parce que tout autre nombre avec zéro dans le dernier chiffre donnera la différence X0-18 plus de trois ou moins que zéro. De la même manière, nous calculons tous les autres nombres:

2 - résidu connu
18 - addition au nombre avec zéro, montrant simultanément la valeur du chiffre suivant - 6 (6 * 3 = 18)
20 est un nombre approprié avec zéro
2 - un nombre à zéro avant de multiplier par 10 (= 20/10)
18 - addition au nombre avec zéro
20 est un nombre approprié avec zéro
...

En conséquence, nous obtenons exactement la même séquence que lors de la division par un coin, mais «d'autre part». Vous pouvez donc calculer «à partir de la fin» la période des fractions périodiques. Et quelle est la pré-période (et l'inefficacité de son calcul pour ce cas de la manière indiquée) nous verrons plus loin. La partie entière du résultat est toujours nulle lors de l'utilisation de l'unité comme dividende, donc encore une fois, nous sommes privés de la nécessité de calculer autre chose, sauf pour la période.

Rappelez-vous maintenant comment nous divisons l'unité en trois: $$ . Tout est simple ici, la période est courte, il n'y a pas de pré-période, cela ne semble rien de remarquable. Mais essayons de multiplier à nouveau le résultat de la division par trois: $$ c'est $$ . Et au début c'était comme ça: $$ . Vous ne remarquez pas la différence? Il y en avait un à l'entrée, et après des actions directes et inverses, nous obtenons ... Comment pourrais-je l'appeler plus facilement? Autrement dit, si nous traçons la chaîne entière des neuf à l'infini, alors nous comprendrons que nous avons une unité, mais ce n'est toujours pas comme ça, pouvez-vous la trouver? Eh bien, pas comme l'original, et c'est tout. Les mathématiciens diront que ce ne sont que deux formes de notation du même nombre, mais la compréhension quotidienne des «mêmes» se rebelle un peu contre de telles définitions. En principe, il est difficile d'être en désaccord avec les mathématiciens, car de nombreux neuf après le point décimal diffèrent de l'unité par quelque chose de complètement éphémère, infiniment petit et tendent à zéro dans la limite. Mais en particulier, pouvez-vous englober avec votre esprit tout cet ensemble d'infinis? Un nombre infini de neuf, une différence infiniment petite, tendant à zéro lors du déplacement d'une série de neuf à l'infini. Et maintenant, comparons cela avec un tel record - 1. Un signe - et tout est clair pour nous. Et combien de signes y avait-il dans les discussions sur l'égalité d'un nombre infini de neuf à un? Autrement dit, il y a encore une différence? Ou votre cerveau ignore-t-il facilement de telles bagatelles dans un ensemble de différences? Mais si nous n'allons pas au regard mental sans fin dans la liste des neuf, alors à l'endroit où nous nous arrêtons, il y aura immédiatement une différence que même les mathématiciens reconnaissent comme significative - si vous ne voyez pas tous les neuf autres, alors nous ne sommes pas du tout un. Par conséquent, la question se pose - pouvez-vous voir au plus profond de l'infini? En général, quoi que vous vouliez, les mathématiciens ont ordonné que ce phénomène soit considéré comme le même nombre. Par conséquent, après avoir considéré cette étoile (avec la franchise - une lueur étrange), nous passons à la suivante.

Une conclusion intéressante découle du fait de détecter un nombre infini de neuf - si le diviseur de un est un nombre premier supérieur à 3, alors la période résultante est toujours divisée par 9, bien sûr, par 3, et aussi avec sa longueur plus d'un caractère, par 11, et quand encore plus de personnages - 13, 37, 101 et ainsi de suite. Et tout cela indépendamment du diviseur d'unité, si seulement il était simple et supérieur à trois. Vous pouvez le vérifier vous-même, par exemple, divisez la période 1/7 égale à 142857 par 3, 9, 11, 13, 37.

Eh bien, avant les tas, nous posons une question simple - est-il possible de construire la période vous-même? Oui tu peux. Par exemple, nous voulons obtenir la période 0123456789, pouvons-nous trouver un dividende et un diviseur donnant quelque chose de similaire? Tu peux! Mais sans le chiffre 8. Alors ce sera 1/81. Et pour que le nombre 8 apparaisse à sa juste place, nous devrons ajouter au nombre 81 quelques chiffres après la virgule décimale, ou sans virgule décimale, mais alors de nombreux zéros seront présents dans la période.

Autre régularité - pour certains diviseurs unitaires, nous ne pouvons pas du tout calculer la période, mais simplement la déplacer cycliquement lorsque nous multiplions le dividende (unité) par un nombre quelconque. Par exemple - 1/7 = 0. (142857) et 2/7 = 0. (285714), 5/7 = 0. (714285), 3/7 = 0. (428571) et ainsi de suite. Si le dividende est supérieur à 7, alors toute la partie du résultat de la division ira à la partie avant la virgule décimale, et la période sera toujours composée des six mêmes chiffres, mais à nouveau décalée cycliquement - 25/7 = 3. (571428), 86/7 = 12. (285714) etc. Comment aimez-vous ça? Tout nombre divisé par 7 donne un ensemble des mêmes nombres! Tout! Absolument aucun. Et oui, ces «tous les nombres» sont un nombre infini. Et le résultat comprend toujours 6 des mêmes nombres. De plus, vous comprendrez pourquoi le monde des nombres est si structuré, mais pour l'instant, nous notons que lorsque nous divisons l'unité par 7, nous avons implicitement reçu absolument toutes les informations nécessaires pour calculer la période à partir du résultat de tout autre nombre étant sept, car nous savons maintenant qu'il suffit juste d'en changer cycliquement un. le seul résultat de la division. Autrement dit, il est une fois de plus confirmé qu'il n'est pas nécessaire de traiter la division des nombres, sauf un, par le nombre choisi pour l'étude. Certes, il peut être nécessaire de multiplier par certains nombres et de se souvenir des résultats intermédiaires, mais plus à ce sujet plus tard.

Maintenant, pour une vue plus générale, nous allons montrer la «carte de bataille». Une carte est tracée pour diviser l'unité par le nombre à l'étude, tandis que la division est effectuée dans tous les systèmes numériques avec une base inférieure au nombre à l'étude. La carte n'inclut pas le résultat de la division, c'est-à-dire la période de la fraction en question, mais à la place, la carte contient les résidus obtenus à chaque étape de la division par le «coin». Voici à quoi cela ressemble:


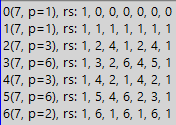
Dans le tableau ci-dessus, vous voyez les lignes, de 0 à 6. 0 est également la base du système de numérotation. Êtes-vous en désaccord? Essayons de convaincre. Qu'est-ce qu'un système numérique? Il s'agit de la base, multipliée par une certaine valeur, puis ajoutée au résultat qui, au tout début, est nul. Ainsi, tous les nombres sont obtenus, par exemple, dans le système de nombres décimaux. Et si la base est nulle? Ensuite, tous les termes multipliés par zéro seront également égaux à zéro. Mais qu'est-ce que cela change? Avons-nous violé la règle de construction des nombres dans le système numérique choisi? Par conséquent, pour la généralité de l'image sur la carte de bataille, nous utilisons tous les systèmes numériques, de 0 à 6 dans le cas de l'étude du nombre 7. Mais en plus de la généralité, la ligne avec des zéros aura un objectif supplémentaire.

Mais que signifient toutes ces lignes? Chaque ligne nous montre la séquence des résidus lors de la division de l'unité par sept dans le système de numérotation, qui est signé dans la colonne la plus à gauche. Autrement dit, lorsque nous divisons 1/7 dans un système avec une base de 0, nous avons un reste initial de 1 (l'unité que nous divisons). De plus, comme nous l'avons toujours fait lors de la division par un coin, nous multiplions le premier reste par la base du système numérique. Nous obtenons zéro. Maintenant, zéro est le reste actuel. Habituellement, lors du calcul du quotient après avoir reçu le reste égal à zéro, et s'il n'y a pas de chiffres supplémentaires dans le nombre divisible, la division est arrêtée (puisque le résultat est obtenu). Mais dans notre cas, nous remplissons un tableau qui ne tolère pas le vide, et en plus de l'impatience, il a des propriétés supplémentaires qui nécessitent également la présence de n'importe quel nombre dans toutes les cellules. Par conséquent, nous continuons à diviser et à diviser le reste de 0 par 7. Habituellement, alors que le reste est plus petit que le diviseur, il est multiplié par la base du système numérique, mais multiplier par zéro plusieurs fois est inutile, donc nous écrivons simplement qu'après avoir multiplié par zéro le reste est à nouveau nul, et Maintenant, mettez-le dans le tableau de la cellule suivante. Répétez ensuite la procédure. Et donc nous remplissons toutes les cellules de la première ligne avec des zéros. Et puis remplissez la deuxième ligne. Mais il a déjà une autre base du système numérique - une unité. Après avoir divisé 1 par 7, nous avons le premier reste - un. Ensuite, nous multiplions par la base du système numérique, c'est-à-dire par un. Nous obtenons à nouveau 1. Nous écrivons dans la cellule appropriée. Encore une fois, nous multiplions par 1, nous obtenons à nouveau 1, nous écrivons à nouveau. Et ainsi de suite jusqu'à ce que la deuxième ligne soit remplie. Mais après ces deux lignes merveilleuses à tous égards, nous arrivons enfin à une division plus significative - dans le système binaire (et la signification des deux premiers systèmes deviendra claire plus tard). Nous avons d'abord la même unité. Écrivez l'unité dans la troisième ligne. Ensuite, nous multiplions par la base du système numérique (par 2). Nous obtenons 2. 2 moins de sept, nous ne pouvons pas encore soustraire, donc nous écrivons le reste 2 dans le tableau. Encore une fois, nous multiplions par 2, nous obtenons 4, ce qui est encore inférieur à 7, donc encore une fois, il va à la table sans changements. Mais à l'étape suivante, nous obtenons 8, ce qui est supérieur à 7, nous devons donc soustraire. Le résultat est 1. Nous écrivons dans le tableau. Mais plus tôt, nous avions déjà une unité, donc toutes les autres étapes seront les mêmes - nous allons donc ajouter la troisième ligne à la fin. Et de la même manière, nous ajouterons le reste des lignes, sans oublier que nous devons multiplier par une autre base du système numérique.

Ainsi, lorsque nous avons finalement obtenu le tableau complet, nous pouvons tirer des conclusions. Tout d'abord, faites attention aux répétitions. Pour le système binaire, nous avons 1,2,4,1,2,4,1, c'est-à-dire deux fois 1,2,4 puis une fois de plus 1. Ici, la liste 1,2,4 correspond à la période de la fraction binaire résultante. Autrement dit, la période sera de longueur 3. Et bien que nous ayons utilisé les restes au lieu des chiffres de la période, la longueur n'a pas souffert de cela, et donc toutes les informations sont enregistrées. Et encore plus - dans le tableau il y a vraiment plus de restes d'informations. Mais plus à ce sujet plus tard, mais pour l'instant, nous notons que toutes les lignes sont faites de la même longueur pour faciliter l'étude et en raison de la présence d'un tel nombre de propriétés utiles. Ainsi, les lignes commencent et se terminent par des unités, ce qui distingue bien les propriétés du nombre 7. Et si nous réduisions les lignes à la longueur de la période, nous ne pourrions pas profiter de la beauté de l'affichage symétrique de l'essence du nombre 7.

Maintenant sur les informations. Les soldes définissent sans ambiguïté le nombre dans la position correspondante de la période, par conséquent, les informations dans cette représentation ne sont pas perdues, mais comme les soldes peuvent être supérieurs, par exemple, au maximum une position décimale (c.-à-d.9), les informations avec leur participation deviennent les plus complètes, car une position dans le système le calcul ne peut pas nous dire que le reste était, par exemple, 19, mais le reste 19 dira clairement quel est le chiffre de la période et à partir de quel reste précédent nous avons soustrait le produit du dividende (rappelez-vous l'accent avec la division «de la fin»). Et d'ailleurs, nous remarquons immédiatement une chose simple - il ne peut y avoir plus de résidus que $$$N-1$où $$$N$- le nombre étudié par lequel nous divisons l'unité. Ceci est un point très important. De plus, il peut être facilement prouvé que si un résidu précédemment rencontré est répété lors de la division par un coin, il y aura alors une répétition de la séquence entière de résidus qui a suivi la valeur précédemment répétée. Nous n'avons donc plus besoin de le prendre, une fois la période trouvée. Si nous enregistrons uniquement les nombres de la période, la répétition des nombres de la période ne signifie pas l'achèvement du calcul. Par conséquent, les soldes sont plus importants que les chiffres de la période. Mais la chose la plus intéressante est les restes de tout $$$N-1$, et donc les périodes sont plus longues $$$N-1$ne peut pas être. Donc, ici, nous venons de trouver la limite supérieure du nombre de chiffres dans la période, passant des chiffres réels de la période aux soldes. Comme on dit, mouvement facile de la main et pas de fraude. C'est l'avantage d'une information plus complète. Eh bien, par conséquent, la largeur de notre «carte de bataille» pour 7 correspondances est de 6 + 1 colonnes, c'est-à-dire 6 colonnes pour tous les résidus possibles et 1 colonne pour détecter la symétrie des unités, ce qui n'est en aucun cas obligatoire pour tous les nombres, et donc ce n'est pas Cela vaut la peine de se cacher, d'économiser de l'espace sous une seule colonne.

Eh bien, jetez maintenant un œil à la «carte» ci-dessus en termes d'utilité. Vous pouvez immédiatement remarquer un ensemble de modèles simples. Chaque ligne commence par une unité et se termine par elle. La deuxième position de chaque ligne indique la base du système de numérotation, mais le milieu de chaque ligne contient soit N-1 ou 1. Notez que nous n'avons fait aucun effort pour organiser les nombres dans le tableau dans l'ordre indiqué, sauf pour simplement fixer les résultats de la division dans le tableau. Mais malgré notre ignorance de tout ordre (à l'exception de la séquence d'étapes de division), l'ordre lui-même est né de nulle part et nous a attiré la lettre P des unités, a mis dessus un capuchon de zéros (avec une visière de l'un), divisé le tableau par une colonne centrale d'unités, et ses ajouts au nombre 7 (selon la formule 7-1 = 6). De plus, la commande elle-même a placé les systèmes de numérotation dans la deuxième colonne. Comparez-le avec les chiffres de la toute première colonne de gauche, ils sont simplement ajoutés intentionnellement, afin que nous sachions exactement où se trouve le système numérique. Eh bien, nous pouvons facilement calculer la période des fractions résultantes nous-mêmes, bien que pour plus de commodité, elle soit indiquée dans la colonne avec des valeurs de la forme p = X.

En fait, devant vous est quelque chose comme un tableau périodique, mais pas pour la chimie, mais pour la théorie des nombres. De la même manière que Mendeleev, vous pouvez simplement regarder dans le tableau trouver un certain modèle, puis, tout comme après Mendeleev, la présence de ce modèle peut être justifiée et prouver qu'il est répété pour tous les nombres satisfaisant un certain ensemble de conditions. Et c'est la chose la plus importante dans ces tableaux. Il suffit de regarder et d'observer des modèles pour découvrir des lois, par exemple la théorie des nombres. Eh bien, pour les lecteurs plus avertis, la route vers un cycle complet s'ouvre ici - après avoir trouvé un modèle, vous devez prouver (ou réfuter) sa pertinence pour tous les nombres, ou pour les nombres d'une certaine classe.

Comme il a été noté, ce tableau contient des informations complètes sur le nombre premier 7. Mais à partir de ces informations, nous pouvons tirer des hypothèses concernant tous les nombres premiers. Et même certaines de ces hypothèses nous ont déjà été prouvées, il nous suffit donc de vérifier les conclusions des autres. Des témoignages ont été fournis par des personnalités telles que, par exemple, Fermat et Euler. La ferme nous a donné cette formule $$$a ^ {(p-1)} \ pmod p = 1$(ici, l'opération de mod prend le reste de la division de la valeur à gauche par la valeur à droite, en programmation, elle est généralement indiquée par le symbole%), c'est-à-dire le reste de la division $$$a ^ {(p-1)}$sur p est toujours égal à un pour tous les nombres premiers (à savoir les nombres premiers, c'est important). Mais le nombre 7 est également premier. Et chaque résidu dans chaque ligne peut être calculé en utilisant la formule suivante: $$$b ^ i \ pmod N = r$. Ici b est la base du système numérique (à partir de la base anglaise), i est le numéro de position dans la ligne (à partir de l'index anglais), à partir de zéro pour la première position, N est le numéro sous enquête (dans ce cas - 7), r est le reste (à partir du rappel anglais) ) formé à la i-ème étape de division par un coin et contenu dans la i-ème colonne du tableau. Comparons la formule de Fermat et la formule de calcul du reste spécifié par l'indice i. Ils sont identiques pour le dernier membre de toutes les séquences de résidus. Et en pleine conformité avec la formule de Fermat, pour chaque reste en position $$$N-1$nous avons l'égalité à l'unité. C'est-à-dire que le modèle observé à l'œil nu sous la forme d'une colonne d'unités a été confirmé et prouvé à l'époque de Fermat (bien que Fermat ne nous ait pas donné de preuves, mais généralement toutes ses déclarations étaient vraies). Euler a ajouté à la formule de Fermat la possibilité de l'utiliser non seulement pour les nombres premiers, mais aussi pour les nombres composites. Certes, vous devez connaître tous les diviseurs d'un nombre, mais pour les petits nombres, ce n'est pas un problème. Ainsi, dans le deuxième tableau (ci-dessous), nous voyons la séquence de résidus pour le nombre 21, qui est composite. Euler a prouvé que le reste de la division d'un nombre arbitraire au degré égal au nombre de nombres plus petits et n'ayant pas de diviseurs communs avec N est également égal à un. Et c'est précisément ce fait que nous observons dans le tableau pour le nombre 21, pour lequel des 20 nombres inférieurs, 8 ont un diviseur commun avec 21, et 12 non. Par conséquent, nous observons dans la 12e colonne (lors de l'indexation à partir de zéro) de nombreuses unités. Et ces unités ne sont pas en fin de ligne, car certains des nombres inférieurs à 21 ont des diviseurs communs avec 21.Mais pour les nombres premiers, pas un plus petit nombre n'a de diviseurs communs avec eux, donc le nombre de nombres sans diviseurs communs en simple est toujours plus grand qu'en composite. Et par conséquent, les résidus unitaires dans le tableau pour les simples sont plus éloignés que pour les composés. Mais notez - toutes les valeurs de la 12e colonne du tableau pour 21 ne sont pas égales à un. Euler a-t-il tort? Non, il n'avait tout simplement pas l'intention d'utiliser sa formule pour travailler avec des nombres qui peuvent être réduits, et juste dans les lignes qui sont des multiples de 3 et 7 (diviseurs de 21), nous avons un écart avec la formule d'Euler. En général, il s'avère que Fermat et Euler nous ont donné des formules appropriées utiles pour comprendre les problèmes de divisibilité des nombres, et les tableaux ci-dessus dans toute leur splendeur confirment les résultats d'Euler et Fermat.


Bien qu'il soit intéressant de noter que ni Fermat ni Euler ne connaissaient le tableau ci-dessus. Et s'ils le savaient, personne n'a été informé d'elle. Bien que, d'autre part, à leur époque, les notations décimales alternatives étaient un peu moins populaires qu'à notre époque. Alors même tout le monde n'était pas au courant du système décimal, mais ils ne comptaient que sur les doigts. Et donc, la Fermat déduite, puis la formule étendue par Euler pour relier la base et le degré, ne nous donnent pas d'explication sur les autres lois de ce tableau. Par conséquent, plus d'étoiles nous attendent, puis la période de l'ouverture conditionnelle des coquilles d'électrons des atomes, avec laquelle les chimistes ont finalement expliqué les propriétés prédictives magiques du tableau périodique. Mais commençons par la magie.

Des étoiles à la magie

Les amateurs de puzzles connaissent les soi-disant «carrés magiques». Ce sont des tableaux dans lesquels vous devez organiser les nombres de manière à ce que les sommes le long des verticales, des horizontales et des deux diagonales soient identiques. Beaucoup de gens ont été perplexes encore et encore pendant longtemps en mettant des chiffres dans le lit procrustien des restrictions sur les montants, et ont même réussi à remplir des carrés assez grands. Mais aujourd'hui, nous avons rencontré une magie beaucoup plus puissante. Oui, le tableau périodique de la théorie des nombres contient beaucoup plus de restrictions, et même un élève de première année qui peut apprendre à partager le «coin» peut le remplir. Pensez-y - les gens les plus intelligents remplissaient les carrés magiques, mais ils n'avaient pas trouvé de méthode commune de remplissage, ni même avancé en taille pour une misérable centaine de colonnes. Et le premier élève fera face à un milliard de dollars, si seulement il avait suffisamment de temps disponible.Voici une telle galaxie, remplie d'étoiles aux globes oculaires, qui nous attend dans des carrés numériques.

Commençons à lister les modèles évidents

Multiplication N'importe quelle ligne du tableau peut être multipliée par une autre. Le résultat sera une série dont le nombre est calculé comme le produit des nombres de la série multipliée divisé par le reste par le nombre à l'étude. Autrement dit, si nous multiplions la ligne 2 du tableau pour 7 par la ligne 3, alors nous obtenons la ligne 6. Et si nous multiplions la ligne ligne 4 par la ligne 6, nous obtenons 24 mod 7 = 3, c'est-à-dire la troisième ligne. Et la propriété même de la division modulo (c'est-à-dire avec le reste) rend inutiles tous les systèmes numériques, plus grands que le nombre étudié. Nous n'avons donc pas besoin d'un système numérique avec la base 24, car les valeurs des résidus y seront exactement les mêmes que dans le système avec la base 3. Dans n'importe quel système numérique, nous calculons les restes à partir de la division 1/7, nous obtenons toujours un résultat qui est déjà est dans le tableau. Intéressant? Et ce n'est que le début.

Symétrie Chaque deuxième colonne contient les parties supérieure et inférieure, qui sont le reflet l'une de l'autre. Et les colonnes restantes contiennent des valeurs égales au complément de la balance réfléchie N. C'est-à-dire que dans la deuxième colonne du tableau pour le chiffre 7, le chiffre 1 complète 6 à 7, 2 complète 5 et 3 complète 4. Par conséquent, la formule considérée ci-dessus$$$b^i \pmod N = r$

$$$(N-j)^i \pmod N = r$
$$$j^i \pmod N = r$
$$$j=N-b$



La symétrie horizontale est exprimée par les colonnes d'unités extrêmes mentionnées précédemment et la colonne d'unités du milieu et son complément à N. Cela fonctionne exactement pour les nombres premiers, mais pour les constituants, il y a des écarts. De plus (là encore uniquement pour les nombres premiers, mais parfois aussi pour les constituants), la colonne centrale de division commence toujours soit par une unité de la période de répétition des résidus, soit donne à droite une série d'additions à N pour la moitié gauche de la série. Autrement dit, si l'unité est dans la colonne du milieu, alors la partie gauche se répète. S'il y a un ajout à N, alors le même côté gauche continue, mais après avoir soustrait de N. Ainsi, de l'ensemble du tableau (pour les nombres premiers), vous ne pouvez laisser que le carré supérieur gauche avec le côté$$$(N-1)/2$



Divisibilité supplémentaire. Les rangées de résidus entre les unités (périodes de résidus) peuvent être de longueurs différentes, mais toutes les longueurs de lignes pour les nombres premiers divisent toujours la longueur totale de la table par un entier. Autrement dit, si au moins une ligne entre les unités ne divise pas complètement la longueur totale du tableau, il s'agit d'un nombre composite (comparez les tableaux pour 21 et 7).

Longueur et caractère unique. Chaque ligne de longueur égale et plus courte que la largeur du tableau se compose de deux parties - une série de résidus au milieu, et ensuite une série d'additions à N pour la série initiale de résidus. De plus, toutes les valeurs de la période sont uniques, c'est-à-dire qu'elles ne sont répétées qu'avec la répétition de la période, mais dans la période, elles ne sont jamais répétées.

Multiplication. Si chaque cellule du tableau est multipliée par un entier, on obtient alors soit un décalage cyclique des résidus dans le cas d'une période de durée égale à la largeur du tableau, soit une nouvelle série dans les cas où la période est plus courte que la largeur du tableau. De plus, dans le cas de courtes périodes, toutes les valeurs de la nouvelle série seront uniques, c'est-à-dire qu'aucune d'entre elles ne se trouve dans la série obtenue en divisant l'unité par le nombre à l'étude, ainsi que dans la série obtenue en multipliant par d'autres nombres et dans la série originale, que nous multiplié par une constante. Au total, le nombre de périodes uniques est égal à la largeur du tableau divisée par la longueur de la période (pour les nombres premiers). Et pour les constituants dans toutes les périodes possibles, il n'y a pas de résidus «interdits» qui, multipliés par des lignes divisibles par les diviseurs du nombre étudié, donnent un reste de zéro, mais plus à ce sujet plus tard.

Du fait de la multiplication des séries, on peut obtenir soit un décalage de période cyclique, soit une nouvelle période. La nouvelle période peut également être décalée cycliquement, en la multipliant par d'autres valeurs. La règle générale pour choisir un décalage ou une nouvelle période est simple - si dans la période restante il y a un nombre par lequel nous multiplions, alors nous obtiendrons un décalage cyclique, et s'il n'y a pas un tel nombre, nous obtiendrons une nouvelle série. Et bien sûr, cela s'applique directement aux fractions périodiques, plus précisément à leurs périodes (il est nécessaire de distinguer les périodes des soldes des périodes des nombres dans l'enregistrement de fraction, bien que généralement la différence soit claire par rapport au contexte). Ainsi, dans l'exemple du nombre 7 précédemment montré, nous avons vu que peu importe la façon dont vous multipliez le résultat de la division par 7, nous obtenons toujours le même ensemble de chiffres dans la période, mais décalés cycliquement par rapport à la division standard 1/7. Dans le cas du nombre 7, nous avons une période (en notation décimale) avec une longueur,coïncidant avec la largeur du tableau, par conséquent, aucun autre nombre ne peut y être obtenu (il n'y a plus de soldes disponibles), mais seuls des décalages cycliques sont possibles. Mais il y a un autre point - nous avons partagé dans le système décimal, mais il n'y a pas une telle ligne dans le tableau. Cela signifie que pour le trouver, nous devons diviser 10 par 7 et obtenir le reste - 3. C'est le système numérique avec la base 3 qui répète complètement le comportement du système décimal par rapport aux restes, c'est donc dans la troisième ligne que nous voyons la période complète, c'est-à-dire avec une longueur égale à la largeur de la table. Et pour obtenir la période en termes décimaux des soldes, vous pouvez prendre tout reste et commencer à le diviser par le coin, puis il y aura tous les chiffres de la période de fraction. Le décalage de la période au cours de la multiplication est déterminé en trouvant le reste de la division du facteur par N dans la série des résidus. Le décalage sera égal à l'indice du solde trouvé,c'est-à-dire que nous devons toujours décaler cycliquement la période de droite à gauche du nombre de chiffres égal à l'indice du reste trouvé.

Et quelques dépendances entre les différents nombres étudiés:


Ici, nous voyons des lignes pour les nombres de 2 à 39 dans le système binaire. Faites attention à la rangée du bas. Des colonnes de nombres 1,2,4,8,16,32 en remontent. Après le nombre 32, on voit une colonne de valeurs augmenter d'une unité (25,26,27, ...). Dans la colonne suivante, les valeurs augmentent de trois. Puis le 6, 13, 26, etc. L'augmentation «change» après avoir atteint une valeur supérieure au nombre étudié (la colonne de gauche entre parenthèses, avant la durée de la période). Ainsi, la croissance d'une unité passe à la croissance de deux, puis de trois, etc. En général, toutes ces colonnes commencent par$$$2^i$$$$2^i$$$ , où j est l'incrément lors du décalage d'une ligne vers le haut (supérieur à zéro). Autrement dit, alors que le numéro de ligne est compris entre$2^i/j$$$$2^i/j$ et $$, l'incrément est égal à j. Après avoir traversé la frontière$2^i/(j+1)$$$ , l'incrément devient égal$2^i/(j+1)$$$ , alors la bordure sera$j+1$$$ , après cela l'incrément sera$2^i/(j+2)$$$$j+2$ etc.Exactement la même régularité est caractéristique pour toute base de systèmes numériques, c'est-à-dire que toutes les lignes peuvent être remplacées par des lignes du système numérique 10 (et dans l'image, nous voyons les résultats pour le système binaire), ou toute autre, et en même temps la régularité sera préservée, mais avec le remplacement 2 dans la formule sur une autre base du système numérique.

Ce qui précède n'est pas une liste complète de modèles, mais les amateurs de puzzles ont probablement déjà assez pour essayer de remplir un carré similaire, par exemple, pour les nombres premiers 11, 13, 17. Essayez, mais n'utilisez pas la méthode de division par coin ou d'exponentiation. Soudain, vous découvrirez une autre régularité par laquelle ces carrés sont formés!

Prédictions

Les propriétaires de boules de cristal ont tendance à prédire l'avenir, mais nous pouvons également prédire quelque chose à partir de nos tables. Vous l'avez probablement déjà remarqué - les dernières colonnes paires d'unités ne se trouvent que dans les nombres premiers. Autrement dit, un coup d'œil sur la table suffit pour comprendre si un nombre est un nombre premier ou non. Il s'agit de la première prédiction pour notre boule de cristal. La deuxième prédiction est la période de fraction dans le système numérique$$$k*N-1$$$$k*N+1$$$$k*N-1=10$$$$1/11=0.(09)$

$$$b^i \pmod N$$$$a^{(p-1)} \pmod p = 1$$$$a^{(p-1)/2} \pmod p = \{1,p-1\}$Alors $$$a^k \pmod p = p - (a^{(p-1)/2+k} \pmod p)$




Il est immédiatement clair que très peu de lignes se terminent par une unité, cela indique la nature composite du nombre. Comme Euler l'a montré dans sa formule pour comparer le degré d'un nombre composé avec le reste de 1, l'exposant dans ce cas ne peut pas être égal au nombre composé moins un (c'est-à-dire la valeur qui détermine la position la plus à droite dans le tableau), donc dans le cas du nombre 21, nous voyons la majorité lignes sans unité à la fin. Néanmoins, nous voyons également plusieurs lignes avec des unités. Pourquoi la formule d'Euler n'est-elle pas remplie pour eux? Faites attention à leur période, elle est égale à 2 ou 1. Autrement dit, comme c'est le cas pour de nombreuses formules, la formule d'Euler nous donne une solution de l'ensemble, et dans cet ensemble, il y a des unités garanties exactement aux positions indiquées par la formule, c'est-à-dire avant la dernière place dans le tableau, mais comme la période est courte, alors lui,répéter plusieurs fois, parfois il s'intègre avec succès dans la largeur totale de la table et nous en obtenons un à la fin de certaines lignes. Cette situation est typique de tout un ensemble de nombres, qui sont appelés pseudo-simples, car ils usurpent l'identité de simples, en plaçant des unités dans la ligne droite de certaines lignes. Mais cela ne nous empêche pas de voir ces séries dans lesquelles il n'y a pas d'unité à la fin, et donc cette situation n'affecte en rien la possibilité fondamentale de déterminer la simplicité ou la nature composite du nombre selon le tableau proposé. Bien qu'en réalité, les principes se retrouvent souvent avec des limites de nos capacités, mais plus à ce sujet plus tard.mettre des unités à droite dans certaines rangées. Mais cela ne nous empêche pas de voir ces séries dans lesquelles il n'y a pas d'unité à la fin, et donc cette situation n'affecte en rien la possibilité fondamentale de déterminer la simplicité ou la nature composite du nombre à partir du tableau proposé. Bien qu'en réalité, les principes se retrouvent souvent avec des limites de nos capacités, mais plus à ce sujet plus tard.mettre des unités à droite dans certaines rangées. Mais cela ne nous empêche pas de voir ces séries dans lesquelles il n'y a pas d'unité à la fin, et donc cette situation n'affecte en rien la possibilité fondamentale de déterminer la simplicité ou la nature composite du nombre à partir du tableau proposé. Bien qu'en réalité, les principes se retrouvent souvent avec des limites de nos capacités, mais plus à ce sujet plus tard.

Maintenant, les diviseurs du nombre 21. Leurs périodes commencent et se terminent non pas par des unités, mais par les diviseurs eux-mêmes. La même chose s'applique à toutes les lignes dans des positions qui sont des multiples de diviseurs. Donc, pour le diviseur 3, nous voyons qu'à la ligne n ° 3, la période commence par un triple et se termine par lui. Idem pour la ligne numéro 7 (malgré le fait que la durée de la période y soit égale à un). Et de la même manière, tous les multiples des numéros à trois et sept lignes se comportent de la même manière. Autrement dit, l'absence d'une unité dans les périodes est un signe de détection du diviseur du nombre étudié, ou une valeur qui est un multiple du diviseur. Eh bien, l'unité au tout début d'une telle série nous parle de la durée de la pré-période. Pour un nombre composé, la pré-période n'existe que dans les systèmes numériques qui sont des multiples des diviseurs du nombre. Donc, si vous tombez sur une fraction avec une pré-période, vous devez savoir qu'elle a été obtenue après avoir divisé le nombre composite.La durée de la pré-période est égale au nombre de résidus au début de la série non compris dans la période des résidus. Lors de la division de l'unité par le nombre étudié, la pré-période sera toujours constituée de zéros. Si nous multiplions le résultat de la division par un autre nombre (ou, de manière équivalente, divisons le facteur par N), alors nous obtenons la même période, dont les règles pour la description sont données ci-dessus, plus la partie du résultat de la multiplication du facteur par les bits les plus anciens de la pré-période. Si le nombre multiplié est supérieur à N, une partie des bits les plus significatifs ira à la partie entière du résultat et la pré-période restera de la même longueur.les règles pour la description desquelles sont données ci-dessus, plus la partie du résultat de la multiplication du facteur par une période qui a disparu par les chiffres supérieurs de la pré-période. Si le nombre multiplié est supérieur à N, une partie des bits les plus significatifs ira à la partie entière du résultat et la pré-période restera de la même longueur.les règles pour la description desquelles sont données ci-dessus, plus la partie du résultat de la multiplication du facteur par une période qui a disparu par les chiffres supérieurs de la pré-période. Si le nombre multiplié est supérieur à N, une partie des bits les plus significatifs ira à la partie entière du résultat et la pré-période restera de la même longueur.

Notez que si nous multiplions la table entière pour un nombre composite par un multiple de n'importe quel diviseur du nombre à l'étude, nous obtenons la dégénérescence de la table lorsqu'elle devient presque une copie de la table d'un autre nombre obtenue après avoir réduit la recherche par son diviseur. Donc ci-dessous est un tableau pour le nombre 21 fois 3, et ci-dessous c'est un tableau pour le nombre 7 fois 3. Si vous les comparez, il devient évident que nous avons presque une copie du tableau pour les sept, mais sont trois fois plus larges et hauteur. Une copie complète ne fonctionnera pas, car dans le tableau pour 21 nombres supérieurs à 7 sont valides et dans le tableau pour 7, ces nombres ne sont pas valides. Mais si nous prenons cela en compte et divisons par le reste des valeurs du tableau pour 21 par le nombre 7, alors les tableaux convergeront. Bien que l'exemple de cette quasi-copie puisse garantir qu'en dehors de la sous-table pour 7, à l'intérieur du tableau pour 21,sont, comme mentionné précédemment, des copies complètes, qu'il est logique de supprimer simplement pour faciliter la perception.



De plus, faites attention aux rangées de zéros avec les lignes n ° 7 et n ° 14. Ils nous indiquent clairement la divisibilité du nombre 21, car nous avons multiplié le résultat de la division de 1/21 par 3, ce qui est réduit et donne le résultat 1/7, mais la ligne 7 dans ce cas montre le résultat de la division 7/7, où tous les restes sont 0. La ligne numéro 14 est le résultat de la division 14/7, et là les restes sont égaux à zéro.

Nous rappelons également qu'avant de multiplier le tableau par 3, les lignes 7 et 14 avaient des valeurs qui étaient des multiples de 7, ce qui, si nous multiplions par elles des valeurs contenant un triple diviseur, aboutissait à un multiple de 21. Mais, comme nous nous en souvenons, dans un tel tableau vous pouvez multiplier les lignes, ce qui signifie que toute ligne contenant un reste qui est un multiple de 3, multiplié par le numéro de ligne 7 ou 14, donnera zéro dans la cellule correspondante. Mais la présence de zéro dans le tableau signifie la divisibilité du nombre par la base du système numérique, dans la ligne de laquelle se trouve zéro. Puisque 21 n'est divisible que par 3 et 7, il ne devrait pas y avoir de zéros dans les rangées non multiples de 3 et 7. C'est pourquoi dans toutes les lignes, sauf pour les multiples de 3, nous ne trouverons pas de résidus qui sont des multiples de 3. Autrement dit, si de tels résidus étaient rencontrés, puis en multipliant la ligne avec un tel reste par la ligne 7 ou 14, nous obtiendrions une ligne qui ne coïncide pas avec la ligne zéro, mais contenant des zéros. Seules les lignesles multiples de 3 coïncident avec la ligne zéro après avoir multiplié par les lignes 7 ou 14. Mais la ligne zéro dans le tableau est une. Comment combiner une ligne zéro et zéro résidus lors de la multiplication par trois des lignes 7 et 14? C’est très simple - vous devez interdire l’apparition de plusieurs nombres de 3 dans toutes les lignes, à l’exception du multiple de 3. Mais nous venons juste d’élaborer cette règle, et les lois du tableau restant ont toujours été observées. C'est-à-dire, toujours, d'une manière amusante, la nature elle-même a supprimé (et supprime) les numéros interdits des rangées qui ne lui ont pas été posées. Nous avons ici une prédiction logique de l'algorithme d'action de la nature. Ou tout simplement notre logique? Cela vaut la peine d’envisager.Comment combiner une ligne zéro et zéro résidus lors de la multiplication par trois des lignes 7 et 14? C'est très simple - vous devez interdire l'apparition de plusieurs nombres de 3 dans toutes les lignes, sauf le multiple 3. Mais nous venons de trouver cette règle, et les lois de la table des résidus ont toujours été observées. C'est-à-dire, toujours, d'une manière amusante, la nature elle-même a supprimé (et supprime) les numéros interdits des rangées qui ne leur sont pas posées. Nous avons ici une prédiction logique de l'algorithme d'action de la nature. Ou tout simplement notre logique? Cela vaut la peine d’envisager.Comment combiner une ligne zéro et zéro résidus lors de la multiplication par trois des lignes 7 et 14? C'est très simple - vous devez interdire l'apparition de plusieurs nombres de 3 dans toutes les lignes, sauf le multiple 3. Mais nous venons de trouver cette règle, et les lois de la table des résidus ont toujours été observées. C'est-à-dire, toujours, d'une manière amusante, la nature elle-même a supprimé (et supprime) les numéros interdits des rangées qui ne lui ont pas été posées. Nous avons ici une prédiction logique de l'algorithme d'action de la nature. Ou tout simplement notre logique? Cela vaut la peine d’envisager.Nous avons ici une prédiction logique de l'algorithme d'action de la nature. Ou tout simplement notre logique? Cela vaut la peine d’envisager.Nous avons ici une prédiction logique de l'algorithme d'action de la nature. Ou tout simplement notre logique? Cela vaut la peine d’envisager.

Pourquoi puis-je utiliser les tableaux décrits? Par exemple, ils nous donnent la possibilité de générer des séquences pseudo-aléatoires. Et ces séquences ont un certain nombre de propriétés utiles. Donc, dans chaque séquence de résidus, il n'y a pas de répétitions. Si nous avons besoin de répétitions (pour une imitation plus complète de l'aléatoire), alors nous avons à notre disposition des valeurs de la période de fraction, qui peuvent souvent être répétées. La distribution des résidus de l'ensemble complet de séquences pour les nombres premiers est toujours parfaitement uniforme. Les valeurs d'un certain nombre de résidus sont automatiquement maintenues dans la plage [1, N-1]. Pour obtenir des séquences, nous avons un nombre infini de nombres premiers, ce qui rend le nombre de séquences illimité. La longueur de séquence maximale ne dépasse pas la valeur d'un nombre premier, ce qui donne un moyen simple de prédire cet important paramètre.La présence de plusieurs séquences, avec une période plus courte que N, nous garantit qu'il n'y a pas d'intersection de séquences lors de leur génération parallèle, c'est-à-dire, en chargeant tous les cœurs de processeur, nous n'avons pas à penser aux verrous, aux synchronisations, aux contrôles d'entrée et autres, ce qui augmente considérablement la vitesse de génération parallèle. De plus, l'algorithme de génération (division par coin) est disponible pour les élèves du primaire, et il est également extrêmement facile à mettre en œuvre par programme.De plus, l'algorithme de génération (division par coin) est disponible pour les élèves du primaire, et il est également extrêmement facile à mettre en œuvre par programme.De plus, l'algorithme de génération (division par coin) est disponible pour les élèves du primaire, et il est également extrêmement facile à mettre en œuvre par programme.

Vous pouvez également penser au chiffrement. Vous pouvez prédire la séquence des résidus en connaissant le diviseur d'unité, le système numérique sélectionné et toute valeur de la série chiffrant les données (après tout, vous pouvez chiffrer en sautant certains résidus). Même lorsque certaines méthodes révèlent certaines valeurs de la séquence de chiffrement, le cryptanalyste devra toujours deviner le nombre choisi et la base du système numérique. Si vous sélectionnez deux paramètres à partir de simples commandes d'une douzaine ou de deux milliards (et pour eux, en raison de leur taille modeste, il est très facile de construire un tableau de leurs périodes, ce qui vous permettra de changer instantanément le chiffre au moins toutes les secondes), puis en utilisant la force brute, un tel chiffre ne peut être craqué qu'en ne triant pas moins de 10 ^ 18 paires. Mais même s'ils fissurent un ensemble de données,puis après un certain intervalle (par exemple, chaque message a sa propre paire), la paire de cryptage changera et tout doit être recommencé à nouveau, ce qui peut ne pas fonctionner en raison de l'impossibilité d'obtenir la valeur de la séquence de cryptage pour chaque message (ou même une partie du message, lors du changement de clé après combien de clés octet). Pour un ordinateur ordinaire, c'est une tâche insoluble. Bien qu'ici tout repose sur la découverte de la théorie de la divisibilité suffisante à de telles fins (comme dans le cas du chiffrement asymétrique généralisé).Bien qu'ici tout repose sur la découverte de la théorie de la divisibilité suffisante à de telles fins (comme dans le cas du chiffrement asymétrique généralisé).Bien qu'ici tout repose sur la découverte de la théorie de la divisibilité suffisante à de telles fins (comme dans le cas du chiffrement asymétrique généralisé).

Dans la prochaine série, nous parlerons de la théorie de la divisibilité et des prix qui attendent les lecteurs intéressés.