Geekly articles weekly

Analyse des entretiens d'embauche Google: recherche de relations



Bienvenue dans le prochain article d'une série d' énigmes que j'ai posées lors d'entretiens avec Google avant leur interdiction après la fuite. Depuis lors, j'ai cessé de travailler en tant qu'ingénieur logiciel chez Google et j'ai déménagé au poste de responsable du développement chez Reddit, mais j'ai encore quelques bons sujets. À ce jour, nous avons examiné la programmation dynamique , élevant les matrices à la puissance et à la synonymie des requêtes . Cette fois, une question complètement nouvelle.

Mais d'abord, deux points. Tout d'abord, le travail chez Reddit était génial. Au cours des huit derniers mois, j'ai construit et dirigé la nouvelle équipe de pertinence des annonces et mis en place un nouveau bureau de développement à New York. Peu importe à quel point cela peut être amusant, malheureusement, j'ai trouvé que jusqu'à récemment, je n'avais plus de temps ni d'énergie pour un blog. J'ai peur d'avoir un peu abandonné cette série. Désolé pour le retard.

Deuxièmement, si vous avez suivi les articles, après le dernier numéro, vous pourriez penser que je commencerais à creuser dans les options synonymiques des requêtes. Bien que j'aimerais y revenir un jour, je dois admettre que j'ai perdu tout intérêt pour ce problème en raison d'un changement de travail et jusqu'à présent, j'ai décidé de le reporter. Restez en contact! Je le dois et j'ai l'intention de le rendre. Juste, tu sais, un peu plus tard ...

Avis de non-responsabilité rapide: Bien que l'entretien des candidats soit l'une de mes tâches professionnelles, ce blog présente mes observations personnelles, mes histoires personnelles et mes opinions personnelles. Veuillez ne pas prendre cela pour toute déclaration officielle de Google, Alphabet, Reddit ou de toute autre personne ou organisation.

Rechercher une nouvelle question


Dans un article précédent, j'ai décrit une de mes questions préférées que j'ai utilisée pendant longtemps, avant l'inévitable fuite. Les questions précédentes étaient fascinantes d'un point de vue théorique, mais je voulais choisir un problème un peu plus pertinent pour Google en tant qu'entreprise. Lorsque cette question a été interdite, j'ai voulu trouver un remplaçant, en tenant compte de la nouvelle restriction: rendre la question plus simple .

Maintenant, cela peut sembler un peu surprenant compte tenu du tristement célèbre processus d'entrevue chez Google. Mais à cette époque, un problème plus simple avait du sens. Mon raisonnement comportait deux parties. La première est pragmatique: les candidats ne réagissaient généralement pas très bien aux questions précédentes, malgré de nombreux indices et simplifications, et je ne savais pas toujours pourquoi. La deuxième théorie: le processus d'entrevue devrait diviser les candidats en catégories «mérite d'être embauché» et «ne vaut pas la peine d'être embauché», et j'étais curieux de savoir si cela pourrait être fait un peu plus facilement avec la question.

Avant de clarifier ces deux points, je veux souligner ce qu'ils ne signifient pas . "Je ne sais pas toujours pourquoi une personne a des problèmes" ne signifie pas l'inutilité des questions et que je voulais simplifier l'entretien pour cette raison. Même la question la plus difficile, beaucoup se sont bien débrouillées. Je veux dire, quand les candidats avaient des problèmes, il était difficile pour moi de comprendre ce qu'ils manquaient.

De bons entretiens donnent une vue d'ensemble des forces et des faiblesses du candidat. Il ne suffit pas que le comité de recrutement dise simplement qu'il a «échoué»: le comité détermine si le candidat possède les qualités spécifiques à l'entreprise qu'il recherche. De même, les mots «il est cool» n'aident pas le comité à choisir un candidat fort dans certains domaines, mais douteux dans d'autres. J'ai constaté que des questions plus complexes séparent trop souvent les candidats en ces deux catégories. Dans cette optique, «je ne sais pas toujours pourquoi une personne a des problèmes» signifie «l’incapacité de progresser sur cette question ne donne pas en soi une image des capacités de ce candidat».

La classification des candidats comme «mérite d'être embauchée» et «ne vaut pas la peine d'être embauchée» ne signifie pas que le processus d'entrevue devrait séparer les candidats stupides des candidats intelligents. Je ne me souviens pas d'un seul candidat qui n'était pas intelligent, talentueux et motivé. Beaucoup venaient d'excellentes universités et les autres étaient clairement extrêmement motivés. Passer des entretiens téléphoniques est déjà un bon tamis, et même refuser à ce stade n'est pas un signe de manque de capacité.

Cependant, je me souviens de beaucoup de personnes qui n'étaient pas suffisamment préparées pour l'entretien ou qui travaillaient trop lentement, ou nécessitaient trop de supervision pour résoudre le problème, ou communiquaient de manière peu claire, ou ne pouvaient pas traduire leurs idées en code, ou occupaient un poste qui ne conduirait tout simplement pas son succès à long terme, etc. La définition de «vaut la peine d'être embauchée» est vague et varie selon l'entreprise, et le processus d'entrevue consiste à déterminer si chaque candidat répond aux exigences d'une entreprise particulière.

J'ai lu beaucoup de commentaires reddit se plaignant de questions d'entrevue trop complexes. J'étais curieux de savoir s'il était encore possible de faire une recommandation digne / indigne pour une tâche plus simple. Je soupçonnais que cela donnerait un signal utile sans crier inutilement les nerfs du candidat. Je vais vous parler de mes conclusions à la fin de l'article ...

Avec ces pensées, je cherchais une nouvelle question. Dans un monde idéal, c'est une question assez simple à résoudre en 45 minutes, mais avec des questions supplémentaires pour que les candidats les plus puissants montrent leurs compétences. Il devrait également être compact dans la mise en œuvre, car de nombreux candidats écrivent toujours au tableau. Un gros plus si le sujet est en quelque sorte lié aux produits Google.

Enfin, je me suis installé sur une question qu'un merveilleux googleur a soigneusement décrite et insérée dans notre base de données de questions. Maintenant, j'ai consulté d'anciens collègues et je me suis assuré que la question était toujours interdite, donc vous ne serez certainement pas posé lors de l'entretien. Je le présente sous la forme dans laquelle il me semble le plus efficace, avec des excuses à l'auteur original.

Question


Parlez de mesurer les distances. La main est une unité de mesure de quatre pouces couramment utilisée dans les pays anglophones pour mesurer la hauteur des chevaux. Une année-lumière est une autre unité de mesure égale à la distance parcourue par une particule (ou une onde?) De lumière en un certain nombre de secondes, approximativement égal à une année terrestre. À première vue, ils ont peu en commun les uns avec les autres, sauf qu'ils sont utilisés pour mesurer la distance. Mais il s'avère que Google peut les convertir assez facilement:



Cela peut sembler évident: au final, ils mesurent tous deux la distance, il est donc clair qu'il y a une transformation. Mais si vous y réfléchissez, c'est un peu étrange: comment ont-ils calculé ce taux de conversion? De toute évidence, personne n'a vraiment compté le nombre de mains dans une année-lumière. En fait, vous n'avez pas besoin de prendre cela directement. Vous pouvez simplement utiliser des conversions bien connues:

  • 1 main = 4 pouces
  • 4 pouces = 0,33333 pied
  • 0,33333 pi = 6,3125e - 5 milles
  • 6.3125e - 5 miles = 1.0737e - 17 années-lumière

Le but de la tâche est de développer un système qui effectuera cette transformation. En particulier:

À l'entrée, vous avez une liste de facteurs de conversion (formatés dans la langue de votre choix) sous la forme d'un ensemble d'unités de mesure initiales, d'unités finales et de facteurs, par exemple:

  ft 12
 cour de pied 0.3333333
 etc.

Pour que ORIGINE * MULTIPLICATEUR = DESTINATION. Développez un algorithme qui prend deux valeurs unitaires arbitraires et renvoie le facteur de conversion entre elles.

La discussion


J'aime ce problème car il a une réponse intuitive et évidente: il suffit de convertir d'une unité à une autre, puis à la suivante, jusqu'à ce que vous trouviez la cible! Je ne me souviens pas d'un seul candidat qui a rencontré ce problème et a été complètement perplexe sur la façon de le résoudre. Cela correspond bien à l'exigence d'un problème «plus simple», car les précédents nécessitaient généralement une longue étude et une réflexion avant de trouver au moins une approche de base de la solution.

Néanmoins, de nombreux candidats n'ont pas réussi à réaliser leur intuition comme une solution de travail sans conseils évidents. L'un des avantages de cette question est qu'elle teste la capacité du candidat à formuler le problème (à faire un cadrage) afin qu'il se prête à l'analyse et au codage. Comme nous le verrons, il y a ici une extension très intéressante qui nécessite un nouveau saut conceptuel.

Pour le contexte, le cadrage est l'acte de traduire un problème avec une solution non évidente en un problème équivalent, où la solution est déduite de manière naturelle. Si cela semble complètement abstrait et imprenable, je suis désolé, mais ça l'est. J'expliquerai ce que je veux dire lorsque je présenterai la solution initiale à ce problème. La première partie de la solution sera un exercice de développement et d'application des connaissances algorithmiques. La deuxième partie sera un exercice de manipulation de ces connaissances afin d'arriver à une optimisation nouvelle et non évidente.

Partie 0. Intuition


Avant de creuser plus profondément, explorons à fond la solution «évidente». La plupart des conversions requises sont simples et directes. Tout Américain qui a voyagé en dehors des États-Unis sait que la plupart du monde utilise la mystérieuse unité «kilomètre» pour mesurer les distances. Pour convertir, il vous suffit de multiplier le nombre de miles par environ 1,6.

Nous avons rencontré de telles choses pour la plupart de nos vies. Pour la plupart des unités, il existe déjà une conversion pré-calculée, il vous suffit donc de la consulter dans le tableau correspondant. Mais s'il n'y a pas de conversion directe (par exemple, des mains aux années-lumière), il est logique de construire un chemin de conversion, comme indiqué ci-dessus:

  • 1 main = 4 pouces
  • 4 pouces = 0,33333 pied
  • 0,33333 pi = 6,3125e - 5 milles
  • 6.3125e - 5 miles = 1.0737e - 17 années-lumière

C'était très simple, je viens de proposer une telle transformation en utilisant mon imagination et une table de transformation standard! Cependant, certaines questions demeurent. Y a-t-il un moyen plus court? Quelle est la précision du coefficient? La conversion est-elle toujours possible? Est-il possible de l'automatiser? Malheureusement, ici l'approche naïve échoue.

Partie 1. Décision naïve


C'est bien que le problème ait une solution intuitive, mais en fait, cette simplicité est un obstacle à la résolution du problème. Il n'y a rien de plus difficile que d'essayer de comprendre d'une manière nouvelle ce que vous comprenez déjà - notamment parce que vous en savez souvent moins que vous ne le pensez. Pour illustrer, imaginez que vous êtes venu pour un entretien - et que vous avez cette méthode intuitive en tête. Mais il ne permet pas de résoudre un certain nombre de problèmes importants.

Par exemple, que faire s'il n'y a pas de conversion ? L'approche évidente ne dit rien, est-il vraiment possible de passer d'une unité à une autre. S'ils me donnent mille taux de conversion, il sera très difficile pour moi de déterminer si c'est possible en principe. Si on me demande de faire une conversion entre des unités inconnues (ou inventées) d'un pointeur et d'un jab , alors je n'ai aucune idée par où commencer. Comment une approche intuitive aide-t-elle ici?

Je dois admettre que c'est une sorte de scénario artificiel, mais il y en a aussi un plus réaliste. Vous voyez que mon énoncé du problème ne comprend que des unités de distance. Cela se fait exprès. Et si je demande au système de convertir des pouces en kilogrammes? Vous et moi savons que ce n'est pas possible car ils mesurent différents types, mais l'entrée ne dit rien sur le «type» que chaque unité mesure.

C'est ici qu'une formulation soigneuse de la question permet aux candidats forts de faire leurs preuves. Avant de développer l'algorithme, ils réfléchissent aux cas extrêmes du système. Et une telle déclaration du problème leur donne délibérément l'occasion de me demander si nous allons traduire différentes unités. Ce n'est pas un problème si énorme s'il se produit à un stade précoce, mais c'est toujours un bon signe lorsque quelqu'un me demande à l'avance: «Que devrait retourner le programme si la conversion n'est pas possible?» Poser la question de cette façon me donne une idée des capacités du candidat avant qu'il n'écrive au moins une ligne de code.

Vue graphique

De toute évidence, l'approche naïve ne convient pas, nous devons donc réfléchir à la façon de faire une telle conversion? La réponse est de considérer les unités comme un graphique. Il s'agit du premier pas de compréhension nécessaire pour résoudre ce problème.

En particulier, imaginez que chaque unité est un nœud dans un graphique, et qu'il y a un bord du nœud A au nœud B si A peut être converti en B :



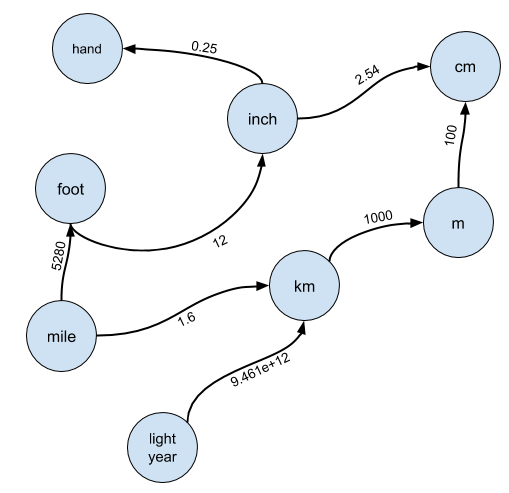
Les bords sont étiquetés avec un taux de conversion par lequel vous devez multiplier A pour obtenir B

Je m'attendais presque toujours à ce que le candidat propose un tel cadrage et lui donnais rarement de sérieux indices. Je peux pardonner au candidat qui ne remarque pas la solution au problème de l'utilisation d'ensembles disjoints ou qui n'est pas trop familier avec l'algèbre linéaire pour réaliser une solution qui se réduit à re-rehausser la puissance de la matrice d'adjacence, mais les graphiques sont enseignés dans n'importe quel programme ou cours de programmation. Si le candidat n'a pas les connaissances appropriées, il s'agit d'un signal «pas d'embauche».

Bref

Une représentation graphique réduit la solution au problème classique de recherche graphique. En particulier, deux algorithmes sont utiles ici: la recherche large (BFS) et la recherche approfondie (DFS). Lors de la recherche en largeur, nous examinons les nœuds en fonction de leur distance par rapport à l'origine:


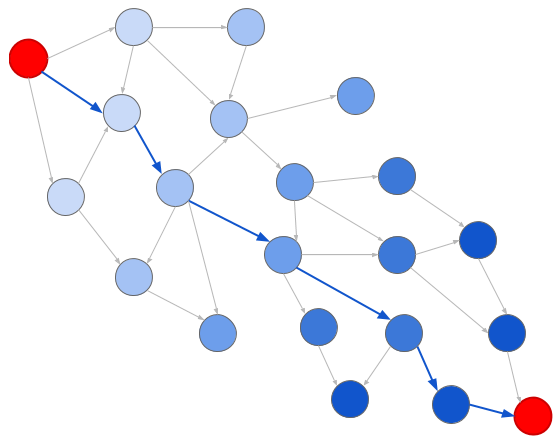Les bleus plus foncés signifient les générations futures

Et lors d'une recherche approfondie, nous examinons les nœuds dans l'ordre dans lequel ils se produisent:



Les bleus plus foncés signifient également les générations futures. Veuillez noter que nous ne visitons pas réellement tous les sites

N'importe lequel des algorithmes détermine facilement s'il y a une conversion d'une unité à une autre, il suffit de rechercher simplement le graphique. Nous partons de l'unité source et recherchons jusqu'à ce que nous trouvions l'unité de destination. Si vous ne trouvez pas votre destination (comme si vous tentiez de convertir des pouces en kilogrammes), nous savons qu'il n'y a aucun moyen.

Mais attendez, il manque quelque chose. Nous ne voulons pas chercher un moyen, nous voulons trouver un taux de conversion! C'est là que le candidat doit faire le saut: il s'avère que vous pouvez modifier n'importe quel algorithme de recherche pour calculer le taux de conversion en enregistrant simplement l'état supplémentaire au fur et à mesure de votre progression. C'est là que les illustrations n'ont plus de sens, alors plongeons-nous dans le code.

Tout d'abord, vous devez déterminer la structure des données du graphique, nous utilisons donc ceci:

 class RateGraph(object): def __init__(self, rates): 'Initialize the graph from an iterable of (start, end, rate) tuples.' self.graph = {} for orig, dest, rate in rates: self.add_conversion(orig, dest, rate) def add_conversion(self, orig, dest, rate): 'Insert a conversion into the graph.' if orig not in self.graph: self.graph[orig] = {} self.graph[orig][dest] = rate def get_neighbors(self, node): 'Returns an iterable of the nodes neighboring the given node.' if node not in self.graph: return None return self.graph[node].items() def get_nodes(self): 'Returns an iterable of all the nodes in the graph.' return self.graph.keys()

Commençons ensuite avec DFS. Il existe de nombreuses façons de le mettre en œuvre, mais de loin la plus courante est une solution récursive. Commençons par ceci:

 from collections import deque def __dfs_helper(rate_graph, node, end, rate_from_origin, visited): if node == end: return rate_from_origin visited.add(node) for unit, rate in rate_graph.get_neighbors(node): if unit not in visited: rate = __dfs_helper(rate_graph, unit, end, rate_from_origin * rate, visited) if rate is not None: return rate return None def dfs(rate_graph, node, end): return __dfs_helper(rate_graph, node, end, 1.0, set())

En un mot, cet algorithme commence par un nœud, itère sur ses voisins et visite immédiatement chacun, faisant un appel récursif à la fonction. Chaque appel de fonction sur la pile enregistre l'état de sa propre itération, donc lorsqu'une visite récursive est retournée, son parent continue immédiatement l'itération. Nous évitons de visiter à nouveau le même site en maintenant un ensemble de sites visités dans tous les appels. Nous calculons également le coefficient en attribuant un facteur de conversion entre chaque nœud et la source. Ainsi, lorsque nous rencontrons le nœud / bloc cible, nous avons déjà créé le coefficient de conversion à partir du nœud source, et nous pouvons simplement le renvoyer.

Il s'agit d'une excellente mise en œuvre, mais elle souffre de deux défauts principaux. Premièrement, il est récursif. S'il s'avère que le chemin souhaité consiste en plus d'un millier de sauts, nous volerons avec un petit problème. Bien sûr, cela est peu probable, mais s'il y a quelque chose d'inacceptable pour un service à long terme, c'est un échec. Deuxièmement, même si nous réussissons, la réponse a certaines propriétés indésirables.

En fait, j'ai déjà donné un indice au début du message. Avez-vous remarqué comment Google affiche le taux de conversion de 1.0739e-17 , mais mon calcul manuel donne 1.0737e-17 ? Il s'avère que toutes ces multiplications en virgule flottante font déjà penser à la propagation de l'erreur. Il y a trop de nuances pour cet article, mais l'essentiel est que vous devez minimiser la multiplication en virgule flottante pour éviter les erreurs qui s'accumulent et causent des problèmes.

DFS est un excellent algorithme de recherche. Si une solution existe, elle la trouvera. Mais il lui manque une propriété clé: il ne trouve pas forcément le chemin le plus court. Ceci est important pour nous car un chemin plus court signifie moins de sauts et moins d'erreur en raison des multiplications en virgule flottante. Pour résoudre le problème, nous nous tournons vers BFS.

Partie 2. Solution BFS


À ce stade, si un candidat met en œuvre avec succès une solution DFS récursive et s'arrête dessus, je donne généralement au moins une faible recommandation sur l'embauche de ce candidat. Il a compris le problème, a choisi le cadrage approprié et a mis en œuvre une solution de travail. C'est une décision naïve, donc je n'insiste pas pour l'embaucher, mais s'il a bien fait avec d'autres interviews, je ne recommanderai pas de refuser.

Cela vaut la peine d'être répété: en cas de doute, écrivez une solution naïve! Même si elle n'est pas complètement optimale, la présence de code sur la carte est déjà une réussite, et souvent la bonne solution peut être trouvée sur sa base. Je dirai différemment: ne travaillez jamais pour rien. Très probablement, vous avez pensé à une solution naïve, mais vous ne vouliez pas l'offrir, car vous savez qu'elle n'est pas optimale. Si vous êtes prêt à proposer la meilleure solution dès maintenant, c'est bien, mais sinon, enregistrez les progrès réalisés avant de passer à des choses plus complexes.

A partir de maintenant, parlons des améliorations de l'algorithme. Les principaux inconvénients d'une solution DFS récursive sont qu'elle est récursive et ne minimise pas le nombre de multiplications. Comme nous le verrons bientôt, BFS minimise le nombre de multiplications, et il est également très difficile de l'implémenter récursivement. Malheureusement, nous devrons abandonner la solution récursive DFA, car pour l'améliorer, nous devrons réécrire complètement le code.

Sans plus tarder, je présente une approche itérative basée sur BFS:

 from collections import deque def bfs(rate_graph, start, end): to_visit = deque() to_visit.appendleft( (start, 1.0) ) visited = set() while to_visit: node, rate_from_origin = to_visit.pop() if node == end: return rate_from_origin visited.add(node) for unit, rate in rate_graph.get_neighbors(node): if unit not in visited: to_visit.appendleft((unit, rate_from_origin * rate)) return None

Cette implémentation est fonctionnellement très différente de la précédente, mais si vous regardez de près, elle fait à peu près la même chose, avec un changement significatif: tandis que le DFS récursif enregistre l'état de la route supplémentaire dans la pile d'appels, mettant en œuvre efficacement la pile LIFO, la solution itérative le stocke dans la file d'attente FIFO

Cela implique la propriété «chemin le plus court / moins de multiplications». Nous visitons les nœuds dans l'ordre dans lequel ils se produisent et nous obtenons ainsi des générations de nœuds. Le premier nœud insère ses voisins, puis nous visitons ces voisins dans l'ordre, en collant leurs voisins tout le temps et ainsi de suite. La propriété de chemin le plus court découle du fait que les nœuds sont visités dans l'ordre de leur distance à la source. Par conséquent, lorsque nous rencontrons une destination, nous savons qu'aucune génération antérieure ne pourrait y conduire.

En ce moment, nous avons presque terminé. Vous devez d'abord répondre à quelques questions, et ils sont obligés de revenir à la formulation originale du problème.

Premièrement, la chose la plus triviale à faire si l'unité d'origine n'existe pas? Autrement dit, nous ne pouvons pas trouver le nœud avec le nom donné. En pratique, vous devez effectuer une certaine normalisation des chaînes de sorte que le livre, le livre et lb pointent vers le même nœud «livre» (ou une autre représentation canonique), mais cela dépasse le cadre de notre question.

Deuxièmement, que se passe-t-il s'il n'y a pas de conversion entre les deux unités? Rappelons que dans les données initiales, il n'y a que des conversions entre les unités, et cela ne donne aucune indication sur la possibilité d'en obtenir une autre à partir d'une unité particulière. Cela se résume au fait que les transformations et les chemins sont directement équivalents, donc s'il n'y a pas de chemin entre deux nœuds, alors il n'y a pas de transformation. En pratique, vous vous retrouvez avec des îlots d'unités sans rapport: un pour les distances, un pour les poids, un pour les devises, etc.

Enfin, si vous regardez attentivement le graphique ci-dessus, il s'avère que vous ne pouvez pas convertir entre les mains et les années-lumière avec cette solution. La direction des connexions entre les nœuds signifie qu'il n'y a aucun moyen de passer de la main aux années-lumière. Cependant, cela est assez facile à corriger, car les transformations peuvent être inversées. Nous pouvons changer notre code d'initialisation de graphique comme suit:

 def add_conversion(self, orig, dest, rate): 'Insert a conversion into the graph. Note we insert its inverse also.' if orig not in self.graph: self.graph[orig] = {} self.graph[orig][dest] = rate if dest not in self.graph: self.graph[dest] = {} self.graph[dest][orig] = 1.0 / rate

Partie 3. Évaluation


C'est fait! Si le candidat a atteint ce point, je le recommanderai très probablement à l'embauche. Si vous avez étudié l'informatique ou suivi un cours d'algorithmique, vous pouvez demander: «Est-ce vraiment suffisant pour obtenir un entretien avec ce type?», Auquel je répondrai: «Essentiellement, oui.»

Avant de décider que la question est trop simple, regardons ce qu'un candidat doit faire pour atteindre ce point:

  • Comprendre la question
  • Construire un réseau de transformations sous forme de graphe
  • Comprendre que les coefficients peuvent être comparés avec les bords du graphique
  • Voir la possibilité d'utiliser des algorithmes de recherche pour y parvenir.
  • Choisissez votre algorithme préféré et modifiez-le pour suivre les cotes
  • S'il a implémenté DFS comme une solution naïve, reconnaissez ses faiblesses.
  • Implémenter BFS
  • Pour prendre du recul et étudier les cas extrêmes:
    • Et si on nous interroge sur un nœud qui n'existe pas?
    • Et si le facteur de conversion n'existe pas?
  • Reconnaître que des transformations inverses sont possibles et probablement nécessaires

Cette question est plus facile que les précédentes, mais elle est également difficile. Comme dans toutes les questions précédentes, le candidat doit faire un saut mental d'une question formulée de manière abstraite à un algorithme ou une structure de données qui ouvre la voie à une solution. La seule chose est que l'algorithme final est moins avancé que dans d'autres problèmes. En dehors de ce matériel algorithmique, les mêmes exigences s'appliquent, en particulier en ce qui concerne les cas extrêmes et l'exactitude.

"Mais attendez!" Vous pouvez demander. - Google n'est-il pas obsédé par la complexité d'exécution? Vous ne vous êtes même pas interrogé sur la complexité temporelle ou spatiale de ce problème. Oh bien! " Vous pouvez également demander: «Attendez une minute, vous avez donné la note« fortement recommandé pour la location »? Comment l'obtenir? " Très bonnes questions, les deux. Cela nous amène à notre dernier tour de bonus supplémentaire ...

Partie 4. Est-il possible de faire mieux?


À ce stade, je tiens à féliciter le candidat pour sa bonne réponse et à préciser que tout ce qui précède n'est qu'un bonus. Lorsque la pression disparaît, nous pouvons commencer à créer.

Quelle est donc la difficulté d'exécuter BFS? Dans le pire des cas, nous devons considérer chaque nœud et bord individuel, ce qui donne une complexité linéaire O(N+E) . Ceci s'ajoute à la même complexité de construction graphique O(N+E) . Pour un moteur de recherche, c'est probablement bon: un millier d'unités de mesure est suffisant pour la plupart des applications raisonnables, et faire une recherche de mémoire pour chaque requête n'est pas une surcharge.

Cependant, on peut faire mieux. Pour motiver, considérez comment ce code est inséré dans la chaîne de recherche. Les conversions de certaines unités non standard sont un peu plus courantes, nous les calculerons donc encore et encore. Chaque fois qu'une recherche est effectuée, des valeurs intermédiaires sont calculées, etc.

Il est souvent suggéré de simplement mettre en cache les résultats des calculs. Chaque fois qu'une conversion d'unité est calculée, nous pouvons toujours simplement ajouter un bord entre les deux conversions. En bonus, nous obtenons la transformation inverse, et gratuitement! Vous avez terminé?

En effet, cela nous donnera un temps de recherche asymptotiquement constant, mais cela coûtera le stockage d'arêtes supplémentaires. Cela devient en fait assez cher: au fil du temps, nous nous efforcerons d'obtenir un graphique complet, car toutes les paires de transformations sont progressivement calculées et stockées. Le nombre d'arêtes possibles dans le graphique est la moitié du carré du nombre de nœuds, donc pour mille nœuds, nous avons besoin d'un demi-million d'arêtes. Pour dix mille nœuds, environ cinquante millions, etc.

Allant au-delà de la portée du moteur de recherche, pour un graphique d'un million de nœuds, nous nous efforçons d'atteindre un demi-billion de bords. Ce montant est tout simplement déraisonnable à stocker, et nous passons du temps à insérer des bords dans le graphique. Nous devons faire mieux.

Heureusement, il existe un moyen d'atteindre un temps constant pour rechercher des coefficients, sans croissance d'espace quadratique. En fait, presque tout ce dont nous avons besoin est juste sous notre nez.

Partie 4. Temps constant


Ainsi, la mise en cache totale est en fait proche de la solution optimale. Dans cette approche, nous obtenons (finalement) des arêtes entre tous les nœuds, c'est-à-dire que notre transformation est réduite à trouver une arête. Mais est-il vraiment nécessaire de stocker les conversions de chaque nœud à chaque nœud? Et si nous enregistrions simplement les facteurs de conversion d' un nœud à tous les autres?

Jetez un autre regard sur la solution BFS:

 from collections import deque def bfs(rate_graph, start, end): to_visit = deque() to_visit.appendleft( (start, 1.0) ) visited = set() while to_visit: node, rate_from_origin = to_visit.pop() if node == end: return rate_from_origin visited.add(node) for unit, rate in rate_graph.get_neighbors(node): if unit not in visited: to_visit.appendleft((unit, rate_from_origin * rate)) return None

Voyons ce qui se passe ici: nous partons du nœud source, et pour chaque nœud que nous rencontrons, nous calculons le coefficient de conversion de la source à ce nœud. Ensuite, dès que nous arrivons à destination, nous retournons le coefficient entre les points de départ et d'arrivée et rejetons les coefficients intermédiaires.

Ces ratios intermédiaires sont essentiels. Mais que se passe-t-il si nous ne les jetons pas? Et si nous les écrivions à la place? Toutes les recherches les plus complexes et incompréhensibles deviennent simples: pour trouver le rapport de A sur B, trouvez d'abord le rapport de X sur B, puis divisez-le par le rapport de X sur A, et vous avez terminé! Visuellement, cela ressemble à ceci:


Notez qu'entre deux nœuds au maximum deux arêtes

Il s'avère que pour calculer ce tableau, nous n'avons presque pas besoin de changer la solution BFS:

 from collections import deque def make_conversions(graph): def conversions_bfs(rate_graph, start, conversions): to_visit = deque() to_visit.appendleft( (start, 1.0) ) while to_visit: node, rate_from_origin = to_visit.pop() conversions[node] = (start, rate_from_origin) for unit, rate in rate_graph.get_neighbors(node): if unit not in conversions: to_visit.append((unit, rate_from_origin * rate)) return conversions conversions = {} for node in graph.get_nodes(): if node not in conversions: conversions_bfs(graph, node, conversions) return conversions

La structure de transformation est représentée par un dictionnaire de l'unité A en deux valeurs: la racine de la composante associée de l'unité A et le coefficient de conversion entre l'unité racine et l'unité A. Puisque nous insérons une unité dans ce dictionnaire à chaque visite, nous pouvons utiliser l'espace clé de ce dictionnaire comme un ensemble de visites au lieu d'utiliser un ensemble de visites dédiées. Notez que nous n'avons pas de nœud final et que nous parcourons plutôt les nœuds jusqu'à ce que nous ayons terminé.

En dehors de ce BFS, il existe une fonction d'assistance qui itère sur les nœuds d'un graphique. Chaque fois qu'il rencontre un nœud en dehors du dictionnaire de traduction, il démarre BFS à partir de ce nœud. , .

, , :

 def convert(conversions, start, end): 'Given a conversion structure, performs a constant-time conversion' try: start_root, start_rate = conversions[start] end_root, end_rate = conversions[end] except KeyError: return None if start_root != end_root: return None return end_rate / start_rate

« » . « » : , , BFS, , . , .

! O(V+E) ( , ), . , , ó , . , : O(V+E) , , O(V) , .

Résultats


, , , , - . - , . , .

( , , , ), « ». , : , , .

. , , , . — . , , Google ( , , ).

, . , , . , , , , - , .

. DFS, , , . , BFS DFS, , , .

, , «», . , , . . , . : , « » .

, !


, , , , . :

-, : , , . , , . , - , - . , , .

-, , , . — : — , A B — / . : , , , , , . .

Enfin, un vrai bijou: certaines unités sont exprimées comme une combinaison de différentes unités de base. Par exemple, un watt est défini dans le système SI comme kg • m² / s³. La dernière tâche consiste à étendre ce système pour prendre en charge la conversion entre ces unités, en ne prenant en compte que les définitions des unités SI de base.

Si vous avez des questions, n'hésitez pas à me contacter sur reddit .

Conclusion


, , . : , , , . , , , , : , . , , , .

J'espère que cet article vous a été utile. Je comprends qu'il peut ne pas y avoir autant d'aventures avec des algorithmes que dans certains articles précédents. Lors des entretiens avec les développeurs, il est habituel de discuter abondamment des algorithmes. Mais la vérité est que d'importantes difficultés surviennent lors de l'utilisation même d'une méthode simple et bien connue. Tout le code est dans le référentiel de cette série d'articles .

Source: https://habr.com/ru/post/fr467371/

More articles:


All Articles