Juste la division, ou comment créer une théorie mathématique et y gagner 400 000 $. Troisième série, finale

Dans les séries précédentes, nous avons examiné les nombres fractionnaires sous plusieurs angles inhabituels. Dans cette série, après l' introduction et quelques bases théoriques , nous allons essayer de tout rassembler sous une forme pratique et de bénéficier des informations disponibles.

Recherche simple

Après avoir parlé des propriétés du tableau des résidus, nous pouvons essayer d'appliquer les connaissances à ce sujet au gain. Ainsi, beaucoup dans le monde trouvent utile de rechercher de grands nombres premiers. Et même il existe des organisations prêtes à donner beaucoup d'argent à quelqu'un qui trouve un grand nombre premier. Mais le sujet de l'informatique quantique est également populaire dans le monde. Pourquoi? Parce qu'il promet de pirater un cryptosystème bien connu. C'est, pour ainsi dire, le slogan publicitaire de l'informatique quantique, qui permet de convaincre tout gestionnaire de prise de décision d'allouer de l'argent pour une leçon aussi intéressante. Par conséquent, nous parlerons également de ce sujet.

Nous allons d'abord vous montrer comment rechercher des nombres premiers. Le problème principal ici est la quantité. Pour les grands nombres, il n'y a tout simplement pas d'algorithmes qui vous permettent de vérifier rapidement si un nombre premier est devant nous ou un nombre composé. Par conséquent, le temps d'arrêt maximal pour aujourd'hui est inférieur à 25 millions de décimales. Cela ne représente que 10 mégaoctets, sur de telles baies, les processeurs modernes affichent des temps de traitement en millisecondes, mais pour vérifier si un nombre premier est dans notre baie, un processeur moderne consommera de l'électricité et bourdonnera avec un ventilateur pendant des décennies. Autrement dit, techniquement, la taille du processeur n'est pas bonne, mais le nombre d'opérations dans des algorithmes connus pour de si grands nombres est tout simplement énorme. Pourquoi cette situation?

Pour les tests de simplicité, par exemple, l'énumération des séparateurs est utilisée. Mais combien de diviseurs devez-vous répéter pour un nombre de dix mégaoctets? La réponse est que même des atomes avec des électrons dans l'univers entier ne suffiront que pour une infime partie de cette valeur. Autrement dit, nous avons besoin d'un grand nombre d'univers, juste pour y placer tous ces diviseurs. Trop? Par conséquent, l'énumération des diviseurs pour les nombres de dix mégaoctets est appliquée dans une mesure limitée (oui, l'univers nous laisse tomber ...), mais heureusement, il existe d'autres algorithmes. Nous pouvons distinguer des algorithmes qui n'utilisent pas l'énumération des diviseurs, et en même temps ils sont garantis pour donner une réponse - simple devant nous ou composite. Mais ce sont des algorithmes très lents. C'est-à-dire, bien sûr, qu'ils sont capables de broyer des nombres de cent ou deux cents bits de cette façon, mais dix mégaoctets pour eux, c'est la mort à la fois. Par conséquent, vous devez sortir des voies délicates.

Mais le problème avec tous les trucs, c'est qu'ils n'ont pas encore trouvé une théorie complète de la divisibilité. Après tout, si elle était complète, nous trouverions très rapidement la réponse - une prime ou non. Plus précisément, une théorie nous donnerait rapidement un algorithme de test qui ne nous ferait pas attendre la mort thermique de l'univers. C'est pourquoi ils donnent des bonus à ceux qui proposent un algorithme le plus rapidement possible, et, mieux encore, une théorie entière pour fournir des algorithmes pour toutes les occasions.

Dans l'intervalle, nous avons à notre disposition un test de Luc-Lemer spécifique, qui utilise la connexion de nombres de Mersenne très spécifiques avec une certaine séquence, mais pas le reste de la division, comme nous l'avons observé récemment, mais la somme des degrés de certains nombres irrationnels. Autrement dit, le test de simplicité a été fait de côté, disons, pas tout à fait évident, bien que certains ici puissent prendre des comparaisons plus compliquées. Mais pourquoi les degrés des nombres irrationnels se sont-ils avérés plus proches des tests de simplicité que toutes les autres réalisations de la théorie des nombres? Apparemment parce que les mathématiques ne connaissent pas de solutions simples. Et en conséquence, une méthode a été utilisée, bien qu'elle ne soit pas évidente mais fonctionne toujours, à partir de la région non la plus proche des calculs entiers, à peu près comment la transition des coordonnées cartésiennes aux coordonnées polaires aide à utiliser des méthodes supplémentaires qui sont très difficiles à implémenter en coordonnées cartésiennes.

En plus du test de Luc-Lemer, il existe également des tests probabilistes. Ils aident à éliminer les nombres composés garantis. Ainsi, l'un des tests probabilistes activement utilisés est un test basé sur la formule de Fermat, dont nous avons récemment parlé. Comment fonctionne-t-il? Très simple - rappelez-vous la colonne d'unités à droite dans le reste du tableau? C'est un signe garanti de la simplicité d'un nombre. Pour expliquer le contrôle en utilisant la formule de Fermat, les mathématiciens utilisent une terminologie spécifique que peu de gens comprennent sauf eux, donc nous n'entrerons pas dans ces jungles mathématiques, mais expliquons tout sur les doigts, ou plutôt, à partir du tableau des résidus. Pour comprendre ce que le reste sera dans la dernière colonne, vous devez soit diviser par une colonne et atteindre le reste à la position contenant 1, soit calculer ce reste en utilisant la formule qui vous permet d'obtenir le reste par le numéro de position et la base du système numérique. La première option pour les nombres de dix mégaoctets nécessitera un temps presque infini, car la largeur de la table est N-1, ce qui signifie que pour un nombre de l'ordre d'un million, il y aura au moins un million de colonnes dans la table. Pour un milliard, un milliard. Pour un billion, un billion. Mais un billion, ce n'est que 12 décimales. Et nous sommes intéressés par un nombre dans lequel moins de 25 millions de caractères. Même un billion de résidus par la méthode de division de la colonne, nous devons calculer à peine moins d'une demi-heure, et ce n'est que 12 décimales. Total! Par rapport à 25 millions. Pensez-vous que vous avez suffisamment de temps pour attendre le résultat de cette façon? C'est pourquoi il est préférable de calculer immédiatement la valeur souhaitée à l'aide de la formule. Et juste la formule de Fermat correspond à la formule de calcul du reste à la dernière position du tableau. De plus, si la période est plus courte que la largeur du tableau, les mathématiques ne savent pas encore comment la calculer, ce qui signifie qu'en tout cas, nous devons choisir la dernière colonne. Les mathématiciens du test vérifient simplement si le reste de la dernière colonne est égal à un pour le système numérique qu'ils ont choisi (bien que les mathématiciens n'utilisent pas le concept du système numérique, pour eux il n'y a qu'une base élevée à une puissance). Si le reste n'est pas égal à un, le nombre est garanti composite. Comme nous l'avons vu dans l'exemple du tableau du nombre 21, c'est l'absence d'une unité au bout de nombreuses lignes qui le distingue des tableaux des nombres premiers. Mais il y a un problème. Sur certaines lignes, il peut encore y avoir des unités, que nous pourrions également vérifier par l'exemple du tableau pour 21. C'est pourquoi les mathématiciens appellent le test basé sur la formule de Fermat probabiliste. Autrement dit, ils ne savent pas si le nombre est premier si le test de Fermat a trouvé un reste égal à un, car de telles fausses unités sont dans le tableau pour le nombre 21, et dans de nombreux autres tableaux, même pour les nombres de dix mégaoctets. Vous devez donc soit vérifier toutes les lignes d'affilée, ce qui est très long, car les lignes d'un nombre de dix mégaoctets, comme indiqué précédemment, sont beaucoup plus que tout ce que nous connaissons dans l'univers, ou tout simplement dire - il est probable que ce nombre soit premier. Voici la dernière méthode choisie par les mathématiciens. Heureusement, il y a peu de lignes se terminant par une dans la plupart des nombres composites. Certes, il y a aussi les soi-disant nombres de Carmichael, dans lesquels toutes les lignes, à l'exception des multiples des diviseurs d'un tel nombre, se terminent par une. Ainsi, sur les nombres de Carmichael, le test probabiliste de la formule de Fermat est pratiquement garanti d'être faux, car pour éliminer l'erreur, vous devez entrer dans un multiple du diviseur de nombre, et dix mégaoctets de diviseurs peuvent avoir seulement deux, et leur valeur peut être très grande, et donc la probabilité d'obtenir c'est dans une telle ligne qu'avec un choix aléatoire de la base du système numérique est pratiquement zéro. Mais d'un autre côté, les nombres de Carmichael sont relativement faibles, ce qui nous permet d'espérer un test probabiliste. Ce n'est que lors de la recherche de nombres premiers que l'espoir de probabilité est exclu. C'est pourquoi, après avoir sélectionné des candidats pour des candidats simples à l'aide de tests de probabilité, le test de Luc-Lemer est néanmoins appliqué.

Ajoutez un peu sur les nombres de Carmichael. Ils sont remarquables non seulement pour leur capacité à imiter les simples. Ainsi, le réseau a un site Web où vous pouvez apprendre différentes séquences de nombres . Si vous entrez le nombre 561 (le nombre minimum de Carmichael) dans le champ de recherche, vous pouvez constater qu'il participe à un très grand nombre de séquences. De quoi parle-t-on? Apparemment, certaines propriétés structurelles encore inconnues de nombres similaires sont très courantes dans notre monde. Fait très amusant.

Mais revenons aux tests de simplicité. Malgré un bon coefficient de filtrage avec des tests probabilistes, l'humanité passe des années à trouver le prochain nombre premier maximum. Pourquoi? Parce que la dépendance du temps d'exécution du test à la taille du nombre est quadratique. Autrement dit, pour les petits nombres, tout se passe bien et il n'y a pas de problème, mais lorsque les nombres augmentent un million de fois, le temps de calcul augmente d'un billion de fois. Par conséquent, sur un seul cœur de processeur, nous considérerions le test de Luc-Lemer pendant des décennies. Mais même un test par la formule de Fermat, nous considérerions à peu près la même chose. Autrement dit, dans les deux approches, le nombre de calculs a atteint les limites des capacités humaines. Vous devez faire quelque chose avec ça, non?

Quelles peuvent être les alternatives à un tel gaspillage informatique sur le chauffage de l'air pendant de nombreuses années? Très simple - vous devez prédire la simplicité par la nature du nombre, par son appartenance à une classe particulière. Les nombres de Mersenne sont donc devenus des leaders dans les tailles obtenues de nombres premiers prouvés précisément en raison de leur appartenance à une classe spécifique. Le test de Luke-Lemer fonctionne spécifiquement pour une classe aussi spécifique. Le nombre d'autres classes est à la traîne en raison de l'absence d'un test aussi coûteux que le test de Luc-Lemer pour les nombres de dix mégaoctets (bien que pour certains, ce test soit adapté). Nous avons donc besoin d'une classification des nombres qui nous permette de trouver des tests de simplicité simples, alors Dieu me pardonne pour un tel jeu de mots.

Comment créer une telle classification? Ce n'est pas non plus si difficile - vous devez étudier différents nombres et identifier les caractéristiques communes entre eux. En général, c'est exactement ce que les mathématiciens essaient de faire, mais jusqu'à présent aucune fleur de pierre n'est sortie. Par conséquent, nous essaierons de les aider.

L'approche décrite précédemment pour l'analyse des nombres sur la base de tableaux de résidus explore essentiellement la divisibilité des nombres de la forme 1000 ... 000. C'est-à-dire que les zéros de droite sont constamment affectés à l'unité, la multipliant ainsi par la base de chacun des systèmes numériques présents dans le tableau restant. À la suite de l'analyse, nous avons constaté que différents nombres divisent les nombres de la forme 1000 ... 000 de différentes manières. Ainsi, les nombres premiers ne peuvent généralement pas diviser un par des zéros. Mais les composants, et même, par exemple, de deux et / ou cinq, sont complètement divisés. Voici le tableau du numéro 8:



Comme vous pouvez le voir, dans les lignes qui sont des multiples de 2, après une entrée de résidus non nuls, il ne reste qu'un zéros. C'est exactement à quoi ressemblent tous les nombres liés à la classe des diviseurs d'unités avec des zéros, et la présence de zéros nous indique dans quels systèmes numériques nous réussirons. Mais voici le problème - du point de vue de la recherche de nombres premiers, une unité avec des zéros n'est pas du tout intéressante pour nous, car elle est garantie d'être divisée par la base du système numérique, ce qui nous donne tous ces zéros après un. Vous devez donc étudier la divisibilité des autres classes de nombres. Est-ce logique? C'est exactement ce que nous allons faire.

Pouvons-nous essayer la théorie de la divisibilité?

Plus tôt, nous avons pris connaissance des régularités des tables restantes pour l'opération de division, qui nous est relativement familière. Les motifs se sont avérés amusants, mais ils ont toujours le même problème - ils ne nous donnent pas d'algorithme rapide pour vérifier la simplicité. Pour un tel test, comme dans le test selon la formule de Fermat, nous devrons augmenter les nombres dans une très large mesure, puis trouver le reste de diviser le résultat par le nombre à l'étude. Ou simplement parcourir tous les restes en utilisant la méthode du «coin» (avant la mort thermique de l'univers, bien sûr). Voici les données - l'opération de montée en puissance avec la recherche du reste prend 15 minutes sur un cœur pour les nombres de commande $$$2 ^ {100000}$. Avec une augmentation de la taille du nombre de 1000 fois, nous obtenons une augmentation quadratique (plus les logarithmes, mais ce n'est pas tellement) au moins 1 000 000 fois, mais en réalité - plusieurs millions de fois. Supposons, par conséquent, que nous obtenions un million d'heures pour un test. Cela représente environ 40 000 jours ou sensiblement plus de cent ans. Si nous optimisons l'exécution du test à ses oreilles, effectuez-le en tenant compte de toutes les caractéristiques de l'architecture du processeur, alors peut-être qu'au lieu d'une centaine d'années nous en avons 10. Sur 10 cœurs - 1 an. Pour 1000 cœurs - 4 jours. Mais ce n'est qu'un test probabiliste, car il existe des masques comme de simples nombres composites. Vous devez donc encore vérifier. Mais le plus important est le fait que le nombre de candidats est de millions. Après toutes les filtrations possibles, il y en aura aussi beaucoup. Par conséquent, le monde joue toujours avec dix numéros mégaoctets.

Mais nous avons un outil. Le tableau restant fonctionne également pour d'autres types de nombres. Par exemple, prenez les chiffres de Mersenne. En binaire, c'est juste une séquence d'unités. Qu'est-ce qui nous empêche d'explorer une séquence d'unités au lieu d'une séquence de zéros? Oui, rien n'empêche. Et il s'avère que pour une telle séquence, notre méthode fonctionne assez bien et un certain nombre de modèles précédemment identifiés y sont conservés. Voici le résultat pour le nombre 7:



Comme nous pouvons le voir, le nombre premier 7 dans tous les systèmes numériques (à l'exception des multiples de sept) est un diviseur des nombres de Mersenne. Autrement dit, presque chaque ligne contient un zéro qui nous indique la divisibilité des nombres de la forme 111 ... 111 (dans le système binaire) par 7. Ainsi, lorsque vous travaillez avec le système de nombres binaires, nous voyons que le nombre 7 divise tous les nombres de Mersenne, la longueur qui est un multiple de 3. Ce résultat est évident sans tableau de résidus - le nombre 7 sous forme binaire se compose de trois unités (111), il divisera donc le nombre binaire de trois unités. Et s'il y a plus d'unités, alors la division ressemble à ceci:

111111 | 111 ------ 111 1001 111 111 111 

Autrement dit, nous avons simplement mis sept (sous forme binaire) sous le dividende. Et combien de fois les sept conviendront - autant d'unités triples dans un nombre divisible. Si en lui le nombre d'unités n'est pas un multiple de trois, alors un tel nombre n'est pas divisible par 7. Mais cela n'est évident que tant que nous étudions des nombres avec une structure identique (7 et 63, comme dans l'exemple). Et si la structure des nombres est plus compliquée, un tableau des résidus nous aidera. Donc, pour tout simple, nous obtenons un résultat similaire, mais avec une période de division légèrement plus longue. Voici un exemple du nombre 11 (le nombre est déjà en décimal):



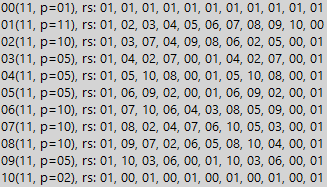
Nous voyons que dans le système binaire la distance à zéro (période de divisibilité) pour le nombre 11 est 10. C'est-à-dire que tout nombre de Mersenne contenant 10k unités, où k est un entier supérieur à zéro, est nécessairement divisible par 11. Il peut être facilement prouvé que les autres sont simples les nombres se comportent exactement de la même manière, sauf pour la taille de la période, bien sûr. Mais pour l'enceinte, la situation est à nouveau moins harmonieuse. Ci-dessous, nous voyons un exemple pour le nombre 8:



Apparemment, 8 ne peut pas diviser les nombres de Mersenne sous forme binaire. Ici, dans le ternaire - s'il vous plaît, mais les nombres de Mersenne se composent uniquement d'unités sous forme binaire. La situation est similaire avec d'autres nombres composés - ils ont tout de différentes manières. L'image mince et symétrique pour les nombres premiers ne se répète pas pour les nombres composés. Mais pour nous, ce sont précisément les simples qui sont importants, car si le nombre est divisé en nombre premier, il n'y a absolument aucun problème s'il est également divisé en un composé qui comprend ce simple. Mais si le nombre n'est pas divisé en un nombre simple, il sera impossible de le diviser en un composé aussi simple. Donc, nous ne devrions nous intéresser qu'aux nombres premiers.

Résumons maintenant. Nous savons que les nombres de Mersenne sont divisés en nombres premiers et que pour la divisibilité, les nombres de Mersenne ont besoin d'un nombre d'unités qui est un multiple de la période de divisibilité du nombre à l'étude. Mais nous savons aussi que les candidats aux nombres premiers de Mersenne ne sont que ceux dont le nombre d'unités est aussi un nombre premier. Autrement dit, ce montant n'est pas divisé en autre chose qu'une unité et lui-même. D'où la conclusion - nous avons besoin d'un tel nombre premier dont la période de divisibilité est égale à la longueur du nombre de Mersenne. Si pour une certaine longueur du nombre de Mersenne nous n'avons pas trouvé de diviseur avec une période appropriée, nous avons devant nous un nombre premier de Mersenne. Cela semble simple.

Mais de nouvelles difficultés commencent. Comment trouver un nombre dont la période coïncide avec la longueur du nombre de Mersenne? Pour répondre à cette question, vous devez résoudre une tâche modeste - trouver un moyen par des moyens simples de trouver la période pour un nombre premier arbitraire. Pour l'instant, nous ne pouvons partager un coin ou piquer à un endroit spécifique en utilisant une formule avec de grands degrés. Mais si nous pouvions calculer la période sans avoir besoin de longs calculs, nous trouverions rapidement le bon diviseur, ou nous nous assurerions qu'il n'y en a pas dans la nature. Exactement la même tâche modeste nous attend dans le cas de l'étude de la divisibilité des nombres de la forme 1000 ... 000. La période de divisibilité est donc très importante à tous égards.

Comment trouver une période?

Ici, les ordinateurs quantiques se précipitent à notre secours. Il était une fois, à une époque immémoriale, un certain connaisseur de la physique quantique du nom de Shor, a suggéré de trouver la période précisément à l'aide d'un ordinateur quantique. En fait, un ordinateur quantique ne donne qu'une valeur intermédiaire, à partir de laquelle un ordinateur ordinaire reçoit alors une période, mais le point n'est pas cela, mais que sans ordinateur quantique, les mathématiques ne sont pas en mesure de calculer la période. Mais en calculant la période, nous avons l'opportunité de calculer avec précision la valeur du reste strictement au milieu de la période. Pourquoi est-ce nécessaire? Pour le fait que vous pouvez en obtenir des facteurs qui contiennent nécessairement une certaine valeur qui est un multiple du diviseur du nombre à l'étude. Cela se fait en ajoutant au reste de l'unité et en soustrayant l'unité. Les deux nombres résultants peuvent être ignorés grâce à un algorithme rapide pour trouver le plus grand diviseur commun avec le nombre à l'étude. Dans au moins un cas, nous obtenons le diviseur du nombre sous enquête. Certes, tout n'est pas si parfait, car comme nous l'avons vu dans l'exemple du tableau des nombres premiers, au milieu de la ligne, il y a souvent un ajout au nombre étudié (N-1), sous cette forme, nous obtenons:

$$

$$N-1 + 1 = N$$

$$

$$N-1-1 = N-2$$

Il en résulte que dans un cas, nous avons le nombre étudié lui-même, et il n'a aucun sens de calculer le plus grand facteur commun, et dans le second cas, nous avons garanti qu'il n'a pas de diviseurs communs avec le nombre étudié. Il n'y a pas de diviseurs communs parce que ce nombre n'est que 2 de moins que le nombre étudié, ce qui signifie que peu importe le nombre qui correspond au nombre entier étudié (ce serait son diviseur), en le soustrayant du nombre étudié, nous obtenons une garantie inférieure valeur que $$$N-2$, ou en utilisant les formules:

$$

$$N / x = k$$

$$

$$(N-x) / x = k-1$$

$$

$$N-x <N-2 \ Rightarrow x> 2 \; \ & \; (N-2) / x \ ne m$$

Ici N est un nombre impair de test (impair parce qu'un multiple de deux est divisible par deux, et nous ne devons diviser par rien), x est un diviseur de N, k est le résultat entier de la division $$$N / x$, m est le résultat de la division $$$(N-2) / x$. Autrement dit, nous devons parfois changer le système numérique et demander à l'ordinateur quantique de trouver une nouvelle période, dans l'espoir qu'au milieu, il y aura un nombre plus approprié. Une limitation plus est la parité obligatoire de la valeur de la durée de la période. Mais tout cela n'est pas si effrayant, car de toute façon, un ordinateur quantique calculera la longueur (ou plusieurs longueurs) dont nous avons besoin beaucoup plus rapidement que la mort thermique de l'univers ne se produit, contrairement à d'autres algorithmes.

Bien que calculer la période d'obtention des diviseurs de nombre soit une tâche légèrement différente de la recherche de simples. Néanmoins, nous pouvons ajouter quelque chose ici en utilisant les tableaux restants. Ainsi, les tableaux montrent que le milieu des lignes de longueur paire est généralement un nombre qui satisfait la condition suivante:

$$

$$r ^ 2 \ pmod N = 1$$

Ici r est le reste souhaité, et N est le nombre sous enquête. Ainsi, il s'avère qu'il n'est pas nécessaire de rechercher une période pour obtenir les diviseurs d'un nombre, car une période est recherchée pour trouver le reste r, puis en ajouter et en soustraire un. Autrement dit, vous pouvez immédiatement trouver ce reste qui satisfait à la condition ci-dessus. Certes, la recherche d'une telle valeur n'est pas non plus triviale. Mais peut-être qu'un ordinateur quantique peut être emprisonné pour une telle chose? Les experts en informatique quantique doivent comprendre combien de qubits sont nécessaires pour cela (les qubits sont ces perroquets qui mesurent la "puissance" d'un ordinateur quantique). Bien que vous puissiez peut-être vous passer d'un ordinateur quantique. Pour ce faire, il vous suffit de comprendre quels modèles vous seront utiles. Certains des modèles sont visibles dans les tableaux de résidus, eh bien, et le reste des lecteurs devront le découvrir par eux-mêmes, et vous craquerez certainement la cryptographie basée sur RSA. Certes, il y a quelques difficultés - vous devez d'abord trouver ces modèles utiles, et ensuite ... Ensuite, ils ne vous paieront peut-être pas. Tout d'abord, les prix donnent pour les grands nombres premiers, pas pour le piratage de RSA. Et deuxièmement - eh bien, pensez par vous-même combien d'organisations sérieuses dans le monde sont intéressées à intercepter les données d'autres personnes de cette manière? Et certains FSB (CIA, Mossad, Mi-5, juste la mafia) ont découvert que vous savez quelque chose. Devinez ce qui va vous arriver? Par conséquent, en outre, vous agissez uniquement à vos propres risques et périls.

Certes, le sujet quantique lui-même est assez intéressant en ce qu'il contient l'incertitude quantique, les fluctuations du vide et d'autres darwinismes quantiques. Comment expliquer tout cela? Pour être honnête, je ne sais pas, mais je vois une analogie avec les autres tableaux. Par exemple, lorsque quelqu'un observe les valeurs dans le tableau résiduel et ne connaît pas les schémas mentionnés précédemment, alors pour lui, il n'y a que du bruit dans le tableau où les nombres se changent de manière aléatoire, comme certaines fluctuations du vide. Mais si vous comprenez que nous appliquons simplement le même algorithme à différentes paires de «séquence - nombre sous enquête», alors toute cette bouillie bouillante à partir des nombres devient instantanément compréhensible. Et de la même manière, il devient clair pourquoi, parmi l'énorme ensemble de valeurs possibles pour remplir la table, seules celles strictement définies y restent vraiment. Mais tant que nous n'obtenons pas l '«interaction» de la séquence avec le nombre étudié, nous ne pouvons pas prédire le contenu du tableau. Plus précisément, tout remplissage sera également probable. Mais après l '«interaction» - tout deviendra strictement logique, à partir du tout aussi probable une seule probabilité naîtra pour une seule option. Et pas parce qu'un certain darwinisme fonctionne, mais seulement à cause de l'application d'un certain algorithme à des données d'entrée spécifiques. Si vous ne connaissez pas l'algorithme, il peut sembler que les lignes du tableau sont en effet de style Darwin. Et si vous savez - tout est très simple. Peut-être qu'en physique quantique il faut rechercher non seulement les particules, mais aussi un algorithme pour leur «division»?

Et encore une fois sur la période

Cependant, la période est très importante pour nous. Oui, c'est ainsi qu'ils vous répondront sur la hot line sur les problèmes brûlants des mathématiques. Comme indiqué ci-dessus, la connaissance de la période permet de comprendre si un nombre a des diviseurs, ou d'une autre manière s'il est premier. Par conséquent, nous continuons sur la période. Jusqu'à présent, nous connaissons un certain nombre de propriétés de période (unicité des valeurs, symétrie avec une longueur paire, etc.), mais nous ne savons pas comment déterminer sa longueur. Bien qu'il y ait une limite supérieure et inférieure - la période ne peut pas être plus longue que le nombre sous enquête moins un, et aussi la période ne peut pas être plus courte que la période de croissance de la base du système numérique jusqu'à ce que le nombre à l'étude soit dépassé (pour sept c'est 3, pour 11 c'est 4, etc. .). Vous pouvez essayer d’appliquer les lois connues à partir des tableaux étudiés et en tirer de nouvelles, mais jusqu’à présent il y a pas mal d’orientations ici, dont la plupart ne mènent pas au succès, bien que jusqu’à ce que vous essayiez chacune, vous ne saurez pas.

Par conséquent, le moyen le plus prometteur est de créer une théorie améliorée de la divisibilité. Sur la base des séquences caractéristiques des résidus, il est possible de révéler les lois de divisibilité de nombreuses classes de nombres. Jusqu'à présent, seules deux classes ont été présentées (nombres de Mersenne et nombres égaux aux degrés du système numérique), mais en réalité il y en a un nombre infini. Comment traiter les connaissances sur toutes les classes de nombres? Seulement dans un travail parallèle massif, et non sous la forme de réchauffeurs d'air en fer, mais sous la forme de personnes travaillant ensemble sur une tâche aussi importante. Le résultat idéal serait la création d'une théorie générale de la divisibilité de toutes les classes de nombres. C'est pour les débutants, puis la divisibilité des polynômes et autres algèbres ira. Mais devrions-nous nous attendre à une telle merveilleuse masse d'esprits humains au cours de la tâche de trouver des nombres premiers? Je suppose que non. Par conséquent, malheureusement, nous avons encore besoin d'autres moyens.

Théoriquement, il existe un tel moyen

Si nous étudions des séquences divisibles alternatives, y compris des valeurs différentes, nous constatons que la période de division de ces séquences croît d'un multiple de la longueur des fragments répétitifs des séquences. Ci-dessous est un exemple d'une séquence divisible de la forme 1010 ... 1010, où zéro et un changent périodiquement. La séquence donnée est toujours divisée en la base du système numérique, mais dans ce cas, la simplicité de l'exemple d'étude des nombres de la classe périodique n'est importante que pour nous, donc nous ne prêtons pas attention à la divisibilité par construction.





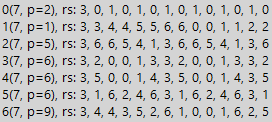
Ici, nous voyons deux tableaux pour le nombre 7 et la séquence indiquée ci-dessus, l'un est normal, et le deuxième tableau est multiplié par 3. D'après les modèles précédemment identifiés dans cet exemple, il y a encore moins, mais, néanmoins, pour les systèmes de nombres sur les bases 1 et 6, nous voyons augmenter la durée de la période $$ . Et pour les tables multipliées par 3, nous constatons une perte de divisibilité pour les bases des systèmes numériques 2 et 5, ce qui est assez amusant en soi (la propriété de divisibilité a changé par rapport à la multiplication). Mais plus important que ça. Il est important de comprendre la possibilité d'appliquer des tables de divisibilité à toutes les séquences. Mais pourquoi avons-nous besoin de séquences? Par exemple, pour augmenter la période minimale de divisibilité.

Si la période minimale peut être allongée, cela nous permet de procéder très simplement à la construction des nombres premiers. Oui, les nombres premiers ne peuvent pas être calculés, mais construits mathématiquement. Lorsque la période est longue, un petit nombre divise un grand, ce qui signifie que si tous les nombres ont des périodes grandes, alors pour les grands nombres, les diviseurs ne peuvent être que de petits nombres. Qu'est-ce que ça donne? Cela permet de retrouver tous les diviseurs d'un grand nombre par une simple recherche. Étant donné que les petits nombres divisent les grands nombres, la taille même de ces petits nombres aide nos ordinateurs à résoudre le problème qu'ils ne peuvent pas résoudre avec de grands diviseurs. Par conséquent, la direction de la recherche des nombres premiers devient claire - nous devons trouver une séquence qui nous donne de grandes périodes minimales. Pourquoi le minimum? Parce que nous ne savons toujours pas comment calculer une période sans énumérer tous les résidus ou élever à une puissance, et donc nous ne pouvons pas simplement trouver une période suffisamment longue si elle est supérieure au minimum, eh bien, nous connaissons la période minimale simplement par l'analyse des tables restantes, c'est-à-dire que nous n'avons pas besoin de la calculer . Eh bien, lorsque nous trouvons la séquence dont nous avons besoin (et juste pour cela, nous pouvons utiliser l'analyse de nombreuses classes de telles séquences), nous sélectionnons simplement la longueur de la séquence qui ne rentrera dans aucune des périodes minimales que nous connaissons. Autrement dit, nous allons ramasser un si grand nombre, qui n'a évidemment pas de diviseurs. Et si sa taille est importante, un prix nous attend. Dans le même temps, nous ne nous intéresserons pas à plus que les périodes minimales, car elles divisent déjà de très grands nombres, que nous atteindrons un peu plus tard.

Il ne reste plus qu'à trouver la bonne séquence. Qui va le prendre? Mais même si nous ne le trouvons pas, alors pour le cryptage mentionné ci-dessus, travailler avec des séquences alternatives permettra d'ajouter un autre terme au chiffrement qui augmente la force cryptographique - maintenant les crackeurs de chiffrement devront deviner la séquence que nous avons choisie, qui peut être un nombre infini. De plus, pour générer des séquences pseudo-aléatoires, nous obtenons la répétabilité des valeurs dans la série des résidus, et pas seulement dans la série de la période de fraction.

Et enfin - les prix!

L'Electronic Frontier Foundation est prête à payer n'importe qui d'abord 150 000 $, puis 250 000 $. Au total - 400 000 $ . Cela ne vous dérangerait-il pas? Alors au point! Mais la chose est simple - vous devez trouver un nombre premier de cent millions de décimales. Cela représente environ 300 millions de bits, soit 40 mégaoctets. Juste à gauche pour dépasser le record actuel 4 fois. Et puis vous avez besoin d'un milliard de chiffres décimaux. C'est déjà 400 mégaoctets. Et tout, pour deux chiffres - 400 000 dollars toujours verts.

En fait, ce ne sont pas des chiffres aussi terribles. Maintenant, si nous pouvions nous éloigner du calcul du reste de la division des grands degrés par le nombre étudié ... Pour les séquences simples de la forme 100 ... 00 et 111 ... 111, le degré est nécessairement présent. Mais peut-être y a-t-il des séquences pour lesquelles la formule de calcul du ième membre d'une série de résidus sera plus simple? Ou vous pouvez vraiment trouver une séquence avec une grande période minimale. Après tout, de quelle période avons-nous besoin? Seulement 300 millions (sous forme binaire). Si une certaine séquence nous donne une période minimale de la forme 100 * N, où N est le nombre sous enquête, alors jusqu'à 3 millions de nombres nous suffiront pour trouver un nombre valant 150k $. Et jusqu'à 30 millions pour un nombre de 250 000 $. Et maintenant, quand une courte période peut se produire en très grand nombre (pour les séquences 100..00 et 111 ... 111), nous n'avons pas de possibilités simples pour la trouver. Mais il y a de l'espoir et tout dépend du choix réussi de la direction de la recherche. Répéter les séquences une par une n'est apparemment pas réaliste pour une seule personne, mais vous pouvez essayer la foule.

Eh bien, lorsque vous trouverez les chiffres requis, une petite bureaucratie vous attend. Vous devez d'abord publier un article dans une revue mathématique aux États-Unis ou en Angleterre ou au Canada ou en Australie, et la revue doit provenir de la liste indiquée par l'Electronic Frontier Foundation (EFF) (ce sont des revues très réputées). Dans l'article, vous devez prouver que votre méthode permet vraiment de trouver le nombre premier souhaité. Ensuite, vous envoyez une lettre de bonheur à l'EFF (à une adresse spécifique), où vous pointez l'article publié et attendez ensuite les commandes de l'EFF. Les commandes peuvent concerner la vérification de tout ce que vous avez fait pour trouver le numéro. Il ne devrait y avoir aucun secret, ni aucune action illégale ou douteuse. Et c'est tout, après cela - votre prix.

Quelles embuscades peuvent vous attendre sur votre chemin? Eh bien, pour commencer - pour trouver un nombre premier et ne pas faire d'erreurs lors de sa recherche. Ensuite, vous devez écrire dans un journal solide. Le magazine étant solide, la réaction habituelle des éditeurs à la lettre du prochain inventeur de la machine à mouvement perpétuel est la suivante:

- Quoi? Un autre monstre? Au panier!

Mais il est possible que vous ayez de l'expérience dans la rédaction d'articles et que vous puissiez facilement faire face à ce problème. Et puis vous trouverez un chèque. Je ne sais pas ce que vos preuves seront étudiées par l'EFF, mais ils écrivent qu'ils peuvent être intéressés par tout, n'importe quoi. Ce sera particulièrement intéressant si les objectifs du FEP ne coïncident pas avec le résultat que vous fournissez. Ils déclarent donc leur objectif de développer des méthodes d'utilisation des ordinateurs personnels pour les mettre à distance temporairement pour l'informatique tierce.Le prix précédent avait été décerné uniquement pour la création et la promotion du programme, que les bénévoles ont téléchargé et ainsi fourni les terraflops nécessaires pour broyer les nombres premiers. Comment l'EFF se rapporte au calcul d'un nombre premier sans terraflops de masse - je ne sais pas. Théoriquement, il n'y a aucune restriction sur leurs exigences, donc le succès est tout à fait possible.

C'est tout, après avoir traversé les deux étapes indiquées (et sans oublier de trouver les numéros nécessaires à l'étape zéro), vous indiquez la banque et le numéro de compte où le prix vous revient. Une grosse somme. Vous traitez la taxe à vos propres frais.

Au lieu d'un épilogue

Il était une fois, Pierre Fermat, n'étant pas mathématicien, a découvert de nombreux modèles de théorie des nombres. L'homme se demandait juste, eh bien, il y avait du temps libre sous la main. Et voici les réalisations dont on se souvient encore. Un autre exemple est Evarist Galois. Il a commencé les mathématiques à l'âge de 16 ans, et à l'âge de 20 ans il est décédé en duel. Pendant 4 ans, il a essayé d'intéresser de nombreux mathématiciens avec ses trouvailles, mais n'a pas réussi. Après la mort, son travail a néanmoins été apprécié et c'est à eux que nous devons la création d'une branche des mathématiques comme la théorie des groupes, ainsi que le développement de l'algèbre. Encore une fois - c'était intéressant pour une personne de trouver les étoiles, mais organiser les œuvres selon les règles n'était pas pour lui. Mais heureusement, son travail a été officialisé par d'autres. Et un autre exemple - George Cantor, réfléchissant sur les concepts bien connus de l'ensemble et de son élément, on a apporté la théorie à la fin du 19ème siècle,que les mathématiciens exceptionnels ont accepté de considérer digne de devenir la base de la reine des sciences.

Pourquoi toutes ces histoires? Comme disait M. Obama, "vous le pouvez!" Oui, ce slogan américain convient parfaitement aux passionnés. Malgré le développement de la science aujourd'hui, elle n'est pas complète, elle n'est pas parfaite, et il y a des endroits où le pied d'un vrai scientifique n'a pas fait un pas. Allumons donc notre curiosité et essayons de rechercher de tels chemins sans entrave, et si vous réussissez?