La nouvelle preuve résout l'approximation de nombres tels que pi

Les anciens Grecs se demandaient s'il était possible d'exprimer grossièrement des nombres irrationnels en fractions. Prouvant l' hypothèse de longue date de Duffin-Schaffer , deux mathématiciens ont donné une réponse exhaustive.

La notation binaire π est infinie. Mais un nombre infini de fractions peut approcher ce nombre avec une précision toujours croissante.

Les creux profonds sur la droite numérique ne sont pas aussi imprenables que cela puisse paraître. C'est l'une des conséquences de nouvelles preuves significatives de la façon dont les nombres complexes se prêtent à de simples approximations.

La preuve résout le problème d'il y a près de 80 ans, connu sous le nom d'hypothèse de Duffin-Shaffer. Ainsi, il donne la réponse finale qui occupe les mathématiciens depuis l'Antiquité: dans quelles conditions est-il possible de représenter des nombres irrationnels d'une durée infiniment longue - comme pi - avec de simples fractions de type 22/7? La preuve établit que la réponse à cette question assez générale se trouve à la suite d'un seul calcul.

«Il existe un critère simple pour savoir si vous pouvez approximer presque n'importe quel nombre ou pratiquement aucun nombre», a déclaré James Maynard de l'Université d'Oxford, co-auteur de la preuve qu'il a faite avec Dimitris Cuculopoulos de l'Université de Montréal.

Les mathématiciens soupçonnent depuis plusieurs décennies que ce critère simple est essentiel pour comprendre quand une bonne approximation peut être obtenue - mais ils n'ont pas pu le prouver. Kukulopoulos et Maynard n'ont pu le faire qu'après avoir reformulé ce problème de nombres en termes de connexions entre les points et les lignes du graphique - un changement cardinal de perspective.

"Je dirais qu'ils étaient suffisamment confiants (et c'était évidemment justifié) pour emprunter la voie choisie", a déclaré Jeffrey Waaler de l'Université du Texas à Austin, qui a contribué aux premiers résultats liés à l'hypothèse Duffin-Schaffer. "Excellent travail."

Éther arithmétique

Avec des nombres rationnels, tout est simple. Ils comprennent des nombres pour compter les objets et tous les autres nombres qui peuvent être écrits en fractions.

En raison de cette capacité à être écrit, les nombres rationnels sont mieux connus de nous. Cependant, parmi tous les nombres réels, les nombres rationnels sont en fait assez peu nombreux. La plupart des nombres sont irrationnels , avec une notation décimale infinie, et ils ne peuvent pas être écrits en fractions. Certains d'entre eux se sont révélés suffisamment importants pour mériter une notation symbolique - pi, e, √2. Le reste ne peut même pas être appelé. Ils sont partout, mais inaccessibles - comme un éther arithmétique.

Par conséquent, il sera peut-être naturel de penser - si nous ne pouvons pas exprimer avec précision des nombres irrationnels, à quel point pouvons-nous nous rapprocher d'eux? Il s'agit d'un domaine d'approximation rationnelle. Les mathématiciens de l'antiquité ont réalisé que le rapport insaisissable de la circonférence au diamètre peut être assez bien approximé en utilisant la fraction 22/7. Plus tard, les mathématiciens ont découvert une approximation encore plus précise et presque identique à pi: 355/113.

«Écrire pi est très difficile», a expliqué Ben Green d'Oxford. «Les gens ont essayé de trouver l'approximation la plus précise de pi, et l'une des façons courantes de le faire était d'utiliser des nombres rationnels.»



En 1837, le mathématicien Peter Gustav Lejeune de Dirichlet a découvert une règle nous indiquant avec quelle précision les nombres irrationnels peuvent être approximés à l'aide de nombres rationnels. L'approximation est facile à trouver si vous ne définissez pas la valeur exacte de l'erreur. Mais Dirichlet a prouvé l'existence d'une relation claire entre les fractions, les nombres irrationnels et les erreurs qui les séparent.

Il a prouvé que pour tout nombre irrationnel, il y a une infinité de fractions qui l'approchent de plus en plus. Plus précisément, l'erreur de chaque fraction ne sera pas supérieure à 1 divisée par le carré du dénominateur. Par exemple, la fraction 22/7 exprime approximativement pi avec une précision de 1/7 ² ou 1/49. La fraction 355/113 n'est pas plus éloignée de pi que 1/113 ² , ou 1/12 769. Dirichlet a prouvé qu'il existe une infinité de fractions, se rapprochant de plus en plus de pi avec un dénominateur croissant.

«Une chose étonnante et remarquable est la capacité d'exprimer grossièrement un nombre réel à travers une fraction, avec une erreur ne dépassant pas une divisée par le carré du dénominateur», a déclaré Andrew Granville de l'Université de Montréal.


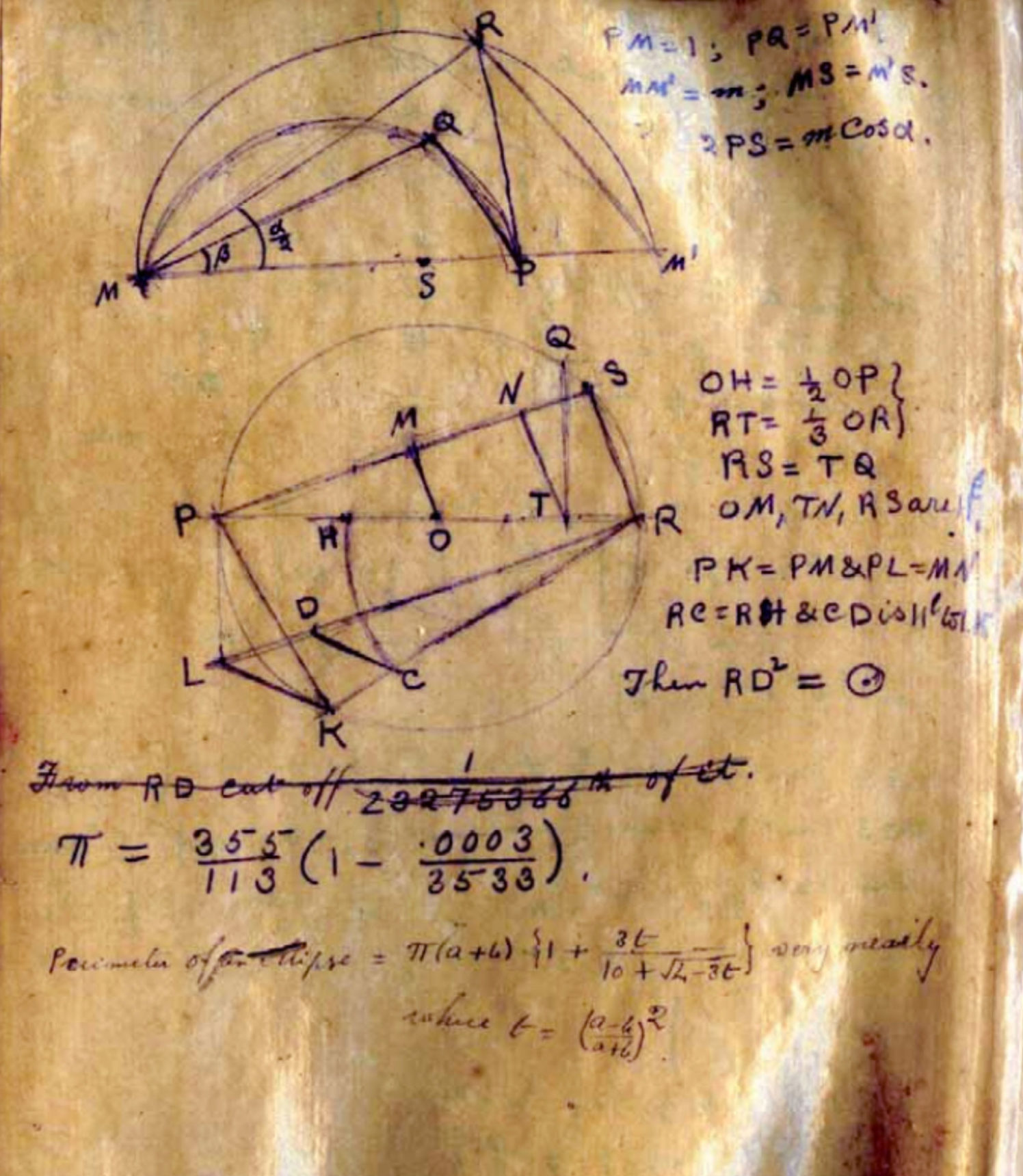Dans le manuscrit de 1913, le mathématicien Srinivasa Ramanujan Iyengor a utilisé la fraction 355/113 comme approximation rationnelle de pi.

La découverte de Dirichlet était une déclaration limitée sur l'approximation rationnelle. Il dit que pour tout nombre irrationnel, vous pouvez trouver une infinité de fractions approchant, si vous pouvez utiliser n'importe quel entier comme dénominateur, et que vous êtes satisfait de l'erreur dans la taille de son carré inverse. Mais que se passe-t-il si vous avez besoin que les dénominateurs appartiennent à un sous-ensemble (infini) d'entiers, par exemple, à l'ensemble des nombres premiers ou à l'ensemble des carrés pleins ? Que se passe-t-il si vous souhaitez que l'erreur d'approximation soit de 0,00001 ou toute autre valeur? Serez-vous capable de trouver une infinité de fractions approximatives précisément dans de telles conditions?

L'hypothèse de Duffin-Shaffer est une tentative de créer la plate-forme la plus généralisée pour travailler avec des approximations rationnelles. En 1941, les mathématiciens R.D.Duffin et A.S. Schafer a présenté le scénario suivant. Tout d'abord, choisissez une liste interminable de dénominateurs. Cela peut être tout ce que vous voulez: des nombres impairs, des nombres divisibles par 10, des nombres premiers.

Ensuite, pour chaque numéro de la liste, sélectionnez la précision avec laquelle vous devez approximer le nombre irrationnel. L'intuition nous dit que si nous choisissons des erreurs suffisamment importantes, nous aurons plus de possibilités d'approximation. Si vous choisissez une petite taille d'erreur, ce sera plus difficile. "N'importe quelle séquence fera l'affaire s'il reste assez de place", a déclaré Kukulopoulos.

Maintenant, étant donné les paramètres sélectionnés - une séquence de nombres et une certaine erreur - la question se pose: est-il possible de trouver une infinité de fractions approximant tous les nombres irrationnels?

L'hypothèse fournit une fonction mathématique pour évaluer cette question. Vos paramètres agissent comme entrée. Le résultat peut être l'une des deux options. Duffin et Schaffer ont suggéré que ces deux options correspondent précisément à la question de savoir si votre séquence peut approximer presque tous les nombres irrationnels avec la précision requise, ou pratiquement aucun d'entre eux («pratiquement» est mentionné parce que pour tout ensemble de dénominateurs, il y aura toujours un petit nombre des nombres irrationnels isolés qui peuvent ou ne peuvent pas être approximés assez bien).

«Vous obtenez presque tout ou presque rien. Il n'y a pas d'options intermédiaires », a déclaré Maynard.

C'était une déclaration extrêmement générale, essayant de caractériser l'approximation par des nombres rationnels le long et à travers. Le critère proposé par Duffin et Schaffer semblait correct aux mathématiciens. Cependant, pour prouver que la sortie binaire de la fonction contient tout ce dont vous avez besoin pour comprendre si votre approximation fonctionne ou non, c'était beaucoup plus difficile à faire.

Double comptage

La preuve de l'hypothèse Duffin-Schaffer est de comprendre quel bénéfice vous tirez de chacun des dénominateurs à votre disposition. Pour ressentir cela, il sera utile d'envisager une version plus petite de cette tâche.

Supposons que vous vouliez approximer tous les nombres irrationnels sur un segment de 0 à 1. Imaginez que tous les nombres naturels de 1 à 10 soient disponibles comme dénominateurs. La liste des fractions possibles est assez grande. D'abord 1/1, puis 1/2 et 2/2, puis 1/3, 2/3 et 3/3, et ainsi de suite, jusqu'à 9/10 et 10/10. Cependant, ils n'en retirent aucun avantage.

Par exemple, 2/10 est identique à 1/5, et 5/10 est identique à 1/2, 2/4, 3/6 et 4/8. Avant l'apparition de l'hypothèse Duffin-Schaffer, le mathématicien soviétique Alexander Y. Khinchin a formulé une hypothèse d'approximation rationnelle similaire en largeur. Cependant, son théorème ne tient pas compte du fait que les fractions équivalentes ne doivent être comptées qu'une seule fois.


Dimitris Cuculopoulos (à gauche) et James Maynard lors de la présentation de son témoignage lors d'une conférence en Italie

"En règle générale, les mathématiques pour la première année ne devraient pas affecter la résolution de problèmes", a déclaré Granville. "Mais dans ce cas, étonnamment, elle a influencé."

Par conséquent, l'hypothèse de Duffin-Shaffer a un terme qui compte le nombre de fractions uniques (ou de fractions réduites) pour chaque dénominateur. Ce membre est appelé la fonction φ d'Euler en l'honneur de son inventeur, le mathématicien du XVIIIe siècle, Leonard Euler. φ (10) est 4, car entre 0 et 1, il n'y a que quatre fractions réduites avec un dénominateur de 10: 1/10, 3/10, 7/10 et 9/10.

L'étape suivante consiste à calculer combien de nombres irrationnels peuvent être approximés en utilisant chacune des fractions données. Cela dépend de l'erreur de taille que vous êtes prêt à accepter. L'hypothèse de Duffin-Shaffer nous permet de choisir une erreur pour chacun des dénominateurs. Par exemple, pour les fractions avec un dénominateur de 7, vous pouvez prendre une erreur admissible de 0,02. Pour le dénominateur 10, vous pouvez prendre l'erreur 0,01.

Après avoir identifié les dénominateurs et les termes des erreurs, il est temps de mettre les réseaux sur des nombres irrationnels. Construisez vos fractions sur une droite numérique entre 0 et 1 et tracez des erreurs sous forme de réseaux s'étendant de la fraction de chaque côté. Nous pouvons dire que tous les nombres irrationnels qui tombent dans le réseau sont «approximativement satisfaisants» pour les termes donnés. La question est: combien de nombres irrationnels avez-vous capturés?



Dans n'importe quel intervalle de la ligne numérique contient un nombre infini de nombres irrationnels, donc le nombre exact de nombres irrationnels capturés ne peut pas être écrit. Au lieu de cela, les mathématiciens parlent de la proportion du nombre total de nombres irrationnels capturés par chaque fraction. Ils évaluent ces proportions en utilisant un concept tel que la «mesure» d'un sous-ensemble de nombres - c'est quelque chose comme estimer le nombre de poissons capturés en poids plutôt qu'en quantité.

L'hypothèse de Duffin-Schaffer suggère d'additionner toutes les mesures des sous-ensembles de nombres irrationnels capturés par chacune des fractions approximatives. Elle représente ce nombre comme une grande somme arithmétique. Puis elle fait sa prédiction principale: si cette somme va à l'infini, alors vous avez approximé presque tous les nombres irrationnels; si elle ne donne que la valeur finale, quel que soit le nombre de mesures que vous avez résumées, vous n'avez pas pu approximer presque n'importe quel nombre irrationnel.

Une question similaire, que la somme «diverge» à l'infini ou «converge» vers une valeur finie, se pose dans de nombreux domaines des mathématiques. L'énoncé principal de l'hypothèse de Duffin-Shaffer est que si vous voulez comprendre si vous pouvez approximer presque tous les nombres irrationnels en utilisant un ensemble donné de dénominateurs et d'erreurs, alors il vous suffit de savoir une chose: la somme infinie de mesures diverge-t-elle vers l'infini ou converge à la valeur finale.

"En fin de compte, quelle que soit la façon dont vous décidez d'évaluer l'approximation pour chaque dénominateur, votre succès dépend entièrement d'une seule chose: que la séquence sans fin diverge ou non", a déclaré Waaler.

Prise de décision

Vous vous demandez peut-être: et si les nombres approchés par une fraction se croisent avec des nombres approchés par une autre? Ne les prendrons-nous pas en compte deux fois dans le calcul des mesures?

Pour certaines séquences d'approximation, le double comptage n'a pas d'importance. Il y a plusieurs décennies, les mathématiciens ont prouvé que cette hypothèse était vraie pour les séquences d'approximation constituées de nombres premiers. Mais pour de nombreuses autres séquences d'approximation, le double comptage est un problème. Par conséquent, les mathématiciens n'ont pas pu traiter cette hypothèse pendant 80 ans.

Le degré auquel différents dénominateurs capturent des ensembles de nombres irrationnels qui se recoupent se reflète dans le nombre de diviseurs simples communs à tous les dénominateurs. Considérez les nombres 12 et 35. Les diviseurs premiers de 12 sont 2 et 3. Les diviseurs premiers de 35 sont 5 et 7. En d'autres termes, les facteurs premiers communs de 12 et 35 ne le font pas - par conséquent, il existe de nombreux nombres irrationnels qui peuvent être approximés par des fractions de les dénominateurs 12 et 35 ne se croisent pas particulièrement.

Qu'en est-il des dénominateurs 12 et 20? En 20, les diviseurs premiers sont 2 et 5 en intersection avec les diviseurs 12. De la même manière, les nombres irrationnels qui peuvent être approximés par des fractions avec un dénominateur de 20 se croisent avec ceux qui peuvent être approximés par des fractions avec un dénominateur de 12. L'hypothèse de Duffin-Shaffer est la plus difficile à prouver dans de telles situations - lorsque les nombres dans la séquence d'approximation ont de nombreux petits diviseurs premiers communs, et que l'intersection de nombreux sous-ensembles de nombres que chacun des dénominateurs approche se produit.

"Lorsque de nombreux dénominateurs parmi lesquels vous choisissez ont de nombreux petits diviseurs simples, ils commencent à interférer les uns avec les autres", a déclaré Sam Chau d'Oxford.

La clé pour résoudre l'hypothèse était de trouver un moyen de calculer avec précision les chevauchements mutuels de sous-ensembles de nombres irrationnels, qui sont approximés par des dénominateurs qui ont des diviseurs premiers communs. Depuis 80 ans, personne n'y est parvenu. Cuculopoulos et Maynard ont réussi, trouvant un point de vue complètement nouveau sur le problème.


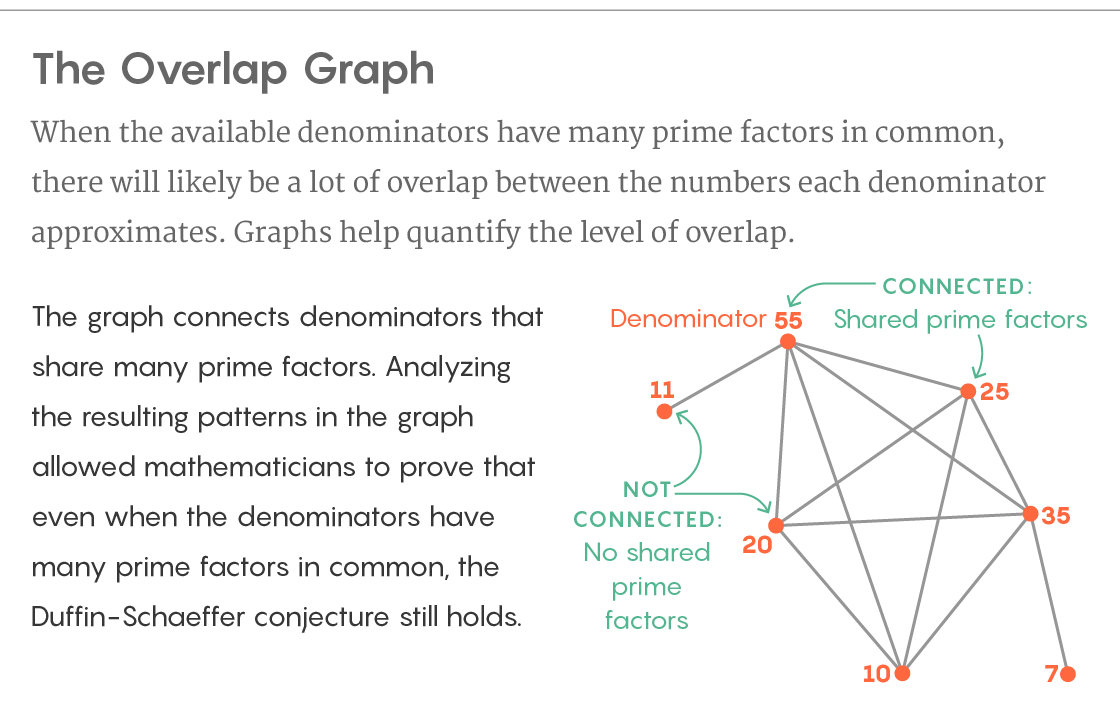Nombre de superpositions mutuelles

Dans leur nouvelle preuve, ils construisent un graphique à partir de leurs dénominateurs. Ils les construisent comme des sommets du graphe et relient les sommets avec une arête s'ils ont plusieurs diviseurs premiers communs. La structure du graphique décrit la superposition des sous-ensembles de nombres irrationnels que chacun des dénominateurs approche. Et bien que cette superposition soit difficile à étudier directement, Kukulopoulos et Maynard ont trouvé un moyen d'analyser la structure du graphique en utilisant des outils de la théorie des graphes - et les informations dont ils avaient besoin ont été trouvées de cette manière.

"Le graphique aide à comprendre visuellement la tâche, c'est une belle langue dans laquelle vous pouvez réfléchir au problème", a déclaré Kukulopulos.

Cuculopoulos et Maynard ont prouvé que l'hypothèse de Duffin-Schaffer est bien vraie: si on vous donnait une liste de dénominateurs avec des erreurs valides, vous pouvez déterminer s'il est possible d'approximer presque tous les nombres irrationnels, ou il est impossible de le faire simplement en vérifiant si la somme correspondante des mesures diverge à l'infini ou converge vers une valeur finie.

Il s'agit d'un test élégant, prenant la vaste question de la nature de l'approximation par des nombres rationnels et la réduisant à une seule valeur calculée. Ayant prouvé l'universalité des tests, Cuculopoulos et Maynard ont fait l'une des plus grandes choses pour les mathématiques: ils ont donné la réponse finale à une question fondamentale dans leur domaine.

"Leur preuve est devenue un résultat nécessaire et suffisant", a déclaré Green. "Je suppose qu'il marque la fin du prochain chapitre en mathématiques."