Le clustering est une partie importante du pipeline d'apprentissage automatique pour résoudre les problèmes scientifiques et commerciaux. Il aide à identifier des ensembles de points étroitement liés (une certaine mesure de distance) dans le nuage de données qui pourraient être difficiles à déterminer par d'autres moyens.

Cependant, le processus de clustering concerne pour la plupart le domaine de l'apprentissage automatique sans enseignant , qui se caractérise par un certain nombre de difficultés. Il n'y a pas de réponses ou de conseils sur la façon d'optimiser le processus ou d'évaluer le succès de la formation. C'est un territoire inexploré.

Par conséquent, il n'est pas surprenant que la méthode populaire de regroupement par la méthode k-average ne réponde pas complètement à notre question: «Comment découvrons-nous d'abord le nombre de clusters?» Cette question est extrêmement importante, car le clustering précède souvent le traitement ultérieur des clusters individuels, et la quantité de ressources informatiques peut dépendre de l'évaluation de leur nombre.

Les pires conséquences peuvent survenir dans le domaine de l'analyse commerciale. Ici, le clustering est utilisé pour la segmentation du marché, et il est possible que le personnel marketing soit affecté en fonction du nombre de clusters. Par conséquent, une estimation erronée de ce montant peut conduire à une allocation non optimale de ressources précieuses.

Méthode du coude

Lors du regroupement à l'aide de la méthode k-means, le nombre de regroupements est le plus souvent estimé à l'aide de la «méthode du coude» . Cela implique une exécution cyclique multiple de l'algorithme avec une augmentation du nombre de clusters sélectionnables, ainsi qu'un report ultérieur du score de clustering sur le graphique, calculé en fonction du nombre de clusters.

Quel est ce score, ou métrique, qui est retardé sur le graphique? Pourquoi est-elle appelée la méthode du coude ?

Un graphique typique ressemble à ceci:



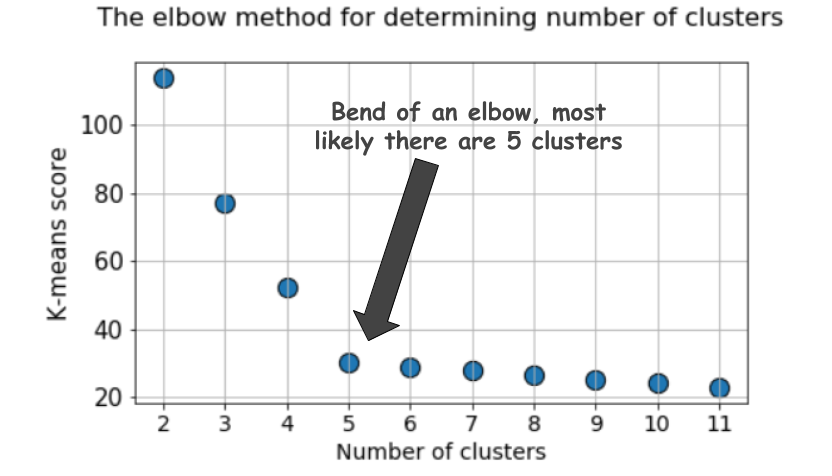
Le score, en règle générale, est une mesure des données d'entrée pour la fonction objective des k-moyennes, c'est-à-dire une certaine forme du rapport de la distance intracluster à la distance intercluster.

Par exemple, cette méthode de notation est immédiatement disponible dans l'outil de notation k-means de Scikit-learn.

Mais jetez un autre regard sur ce graphique. Ça fait quelque chose d'étrange. Quel est le nombre optimal de clusters que nous avons, 4, 5 ou 6?

Ce n'est pas clair, n'est-ce pas?

La silhouette est une meilleure métrique

Le coefficient de silhouette est calculé en utilisant la distance intracluster moyenne (a) et la distance moyenne au cluster (b) le plus proche pour chaque échantillon. La silhouette est calculée comme (b - a) / max(a, b) . Je m'explique: b est la distance entre a et le cluster le plus proche auquel a n'appartient pas. Vous pouvez calculer la valeur de silhouette moyenne pour tous les échantillons et l'utiliser comme métrique pour estimer le nombre de grappes.

Voici une vidéo expliquant cette idée:


Supposons que nous ayons généré des données aléatoires en utilisant la fonction make_blob de Scikit-learn. Les données sont réparties en quatre dimensions et autour de cinq centres de grappes. L'essence du problème est que les données sont générées autour de cinq centres de cluster. Cependant, l'algorithme k-means ne le sait pas.

Les grappes peuvent être affichées sur le graphique comme suit (signes par paires):



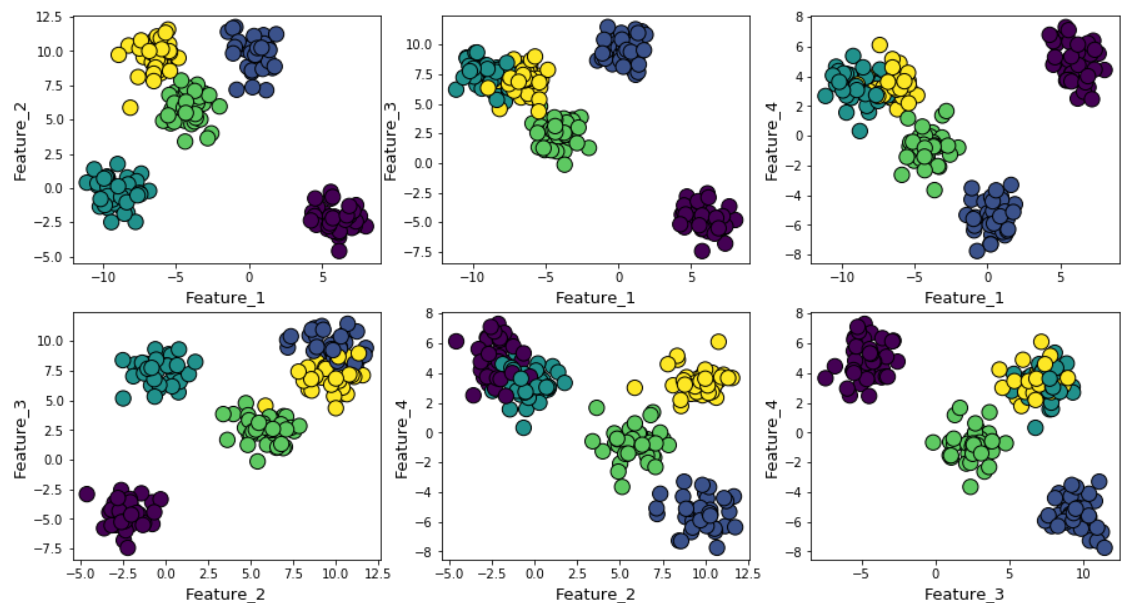
Ensuite, nous exécutons l'algorithme k-means avec des valeurs de k = 2 à k = 12, puis nous calculons la métrique par défaut de k-means et la valeur de silhouette moyenne pour chaque analyse, avec les résultats affichés dans deux graphiques adjacents.



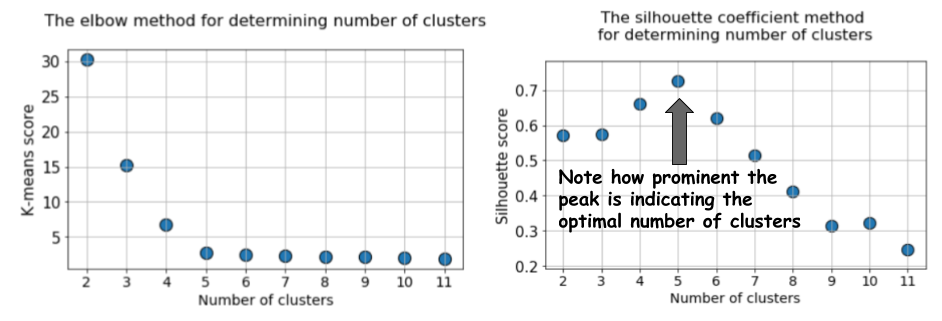
La différence est évidente. La valeur moyenne de la silhouette augmente à k = 5, puis diminue fortement pour des valeurs plus élevées de k . Autrement dit, nous obtenons un pic prononcé à k = 5, c'est le nombre de clusters générés dans l'ensemble de données d'origine.

Le graphique de la silhouette a un caractère de pointe, contrairement au graphique légèrement incurvé lors de l'utilisation de la méthode du coude. Il est plus facile de visualiser et de justifier.

Si vous augmentez le bruit gaussien pendant la génération des données, les clusters se chevaucheront plus fortement.



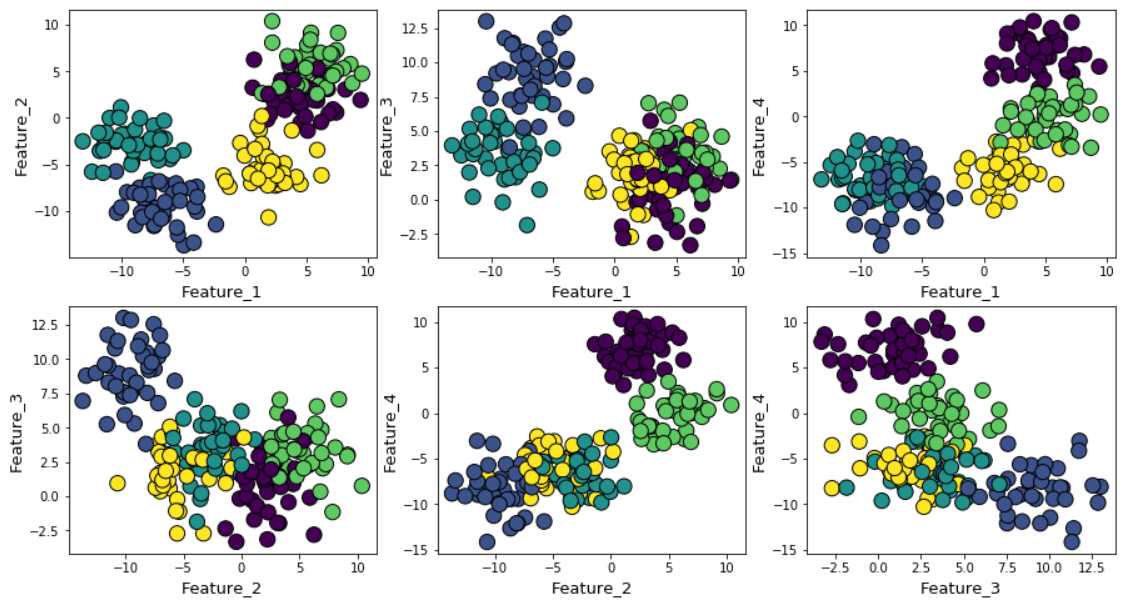
Dans ce cas, le calcul des k-moyennes par défaut en utilisant la méthode du coude donne un résultat encore plus incertain. Voici un graphique de la méthode du coude, où il est difficile de choisir un point approprié auquel la ligne se plie réellement. Est-ce 4, 5, 6 ou 7?



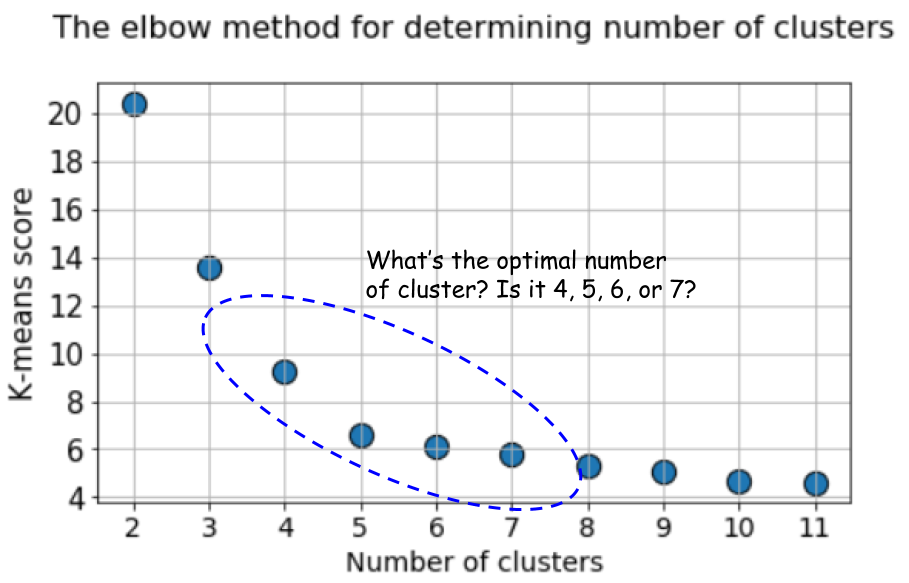
Dans le même temps, le graphique de silhouette montre toujours un pic dans la région de 4 ou 5 centres de cluster, ce qui facilite grandement notre vie.

Si vous regardez les clusters qui se chevauchent, vous verrez que, malgré le fait que nous ayons généré des données autour de 5 centres, en raison de la forte dispersion, seuls 4 clusters peuvent être structurellement distingués. La silhouette révèle facilement ce comportement et montre le nombre optimal de clusters entre 4 et 5.

Score BIC avec un modèle de mix de distribution normal

Il existe d'autres excellentes mesures pour déterminer le nombre réel de clusters, comme le critère d'information bayésien (BIC). Mais elles ne peuvent être appliquées que si nous devons passer de la méthode k-means à une version plus généralisée - un mélange de distributions normales (Gaussian Mixture Model (GMM)).

GMM considère le nuage de données comme une superposition de nombreux ensembles de données avec une distribution normale, avec des valeurs moyennes et des variances distinctes. Et puis GMM utilise un algorithme pour maximiser les attentes afin de déterminer ces moyennes et variances.

BIC pour régularisation

Vous avez peut-être déjà rencontré BIC dans l'analyse statistique ou lors de l'utilisation de la régression linéaire. Le BIC et l'AIC (Akaike Information Criterion) sont utilisés dans la régression linéaire comme techniques de régularisation pour le processus de sélection des variables.

Une idée similaire s'applique au BIC. Théoriquement, les grappes extrêmement complexes peuvent être modélisées comme des superpositions d'un grand nombre d'ensembles de données avec une distribution normale. Pour résoudre ce problème, vous pouvez appliquer un nombre illimité de telles distributions.
Mais cela revient à augmenter la complexité du modèle en régression linéaire, quand un grand nombre de propriétés peuvent être utilisées pour faire correspondre des données de toute complexité, pour ne perdre la possibilité de généralisation, car un modèle trop complexe correspond au bruit, et non à un modèle réel.

La méthode BIC inflige une amende à de nombreuses distributions normales et essaie de garder le modèle suffisamment simple pour décrire un modèle donné.

Par conséquent, vous pouvez exécuter l'algorithme GMM pour un grand nombre de centres de cluster, et la valeur BIC augmentera jusqu'à un certain point, puis commencera à diminuer à mesure que l'amende se développe.

Résumé

Voici le carnet Jupyter pour cet article. N'hésitez pas à bifurquer et à expérimenter.

Chez Jet Infosystems, nous avons discuté de quelques alternatives à la méthode populaire du coude en termes de choix du bon nombre de grappes lors de l'apprentissage sans professeur utilisant l'algorithme k-means.

Nous nous sommes assurés qu'au lieu de la méthode du coude, il est préférable d'utiliser le coefficient de «silhouette» et la valeur BIC (de l'extension GMM pour k-means) pour déterminer visuellement le nombre optimal de grappes.