Salut

Ici, nous décrivons le travail d'un certain domaine et faisons ensuite quelques belles fonctionnalités (tout est TRÈS simple ici).

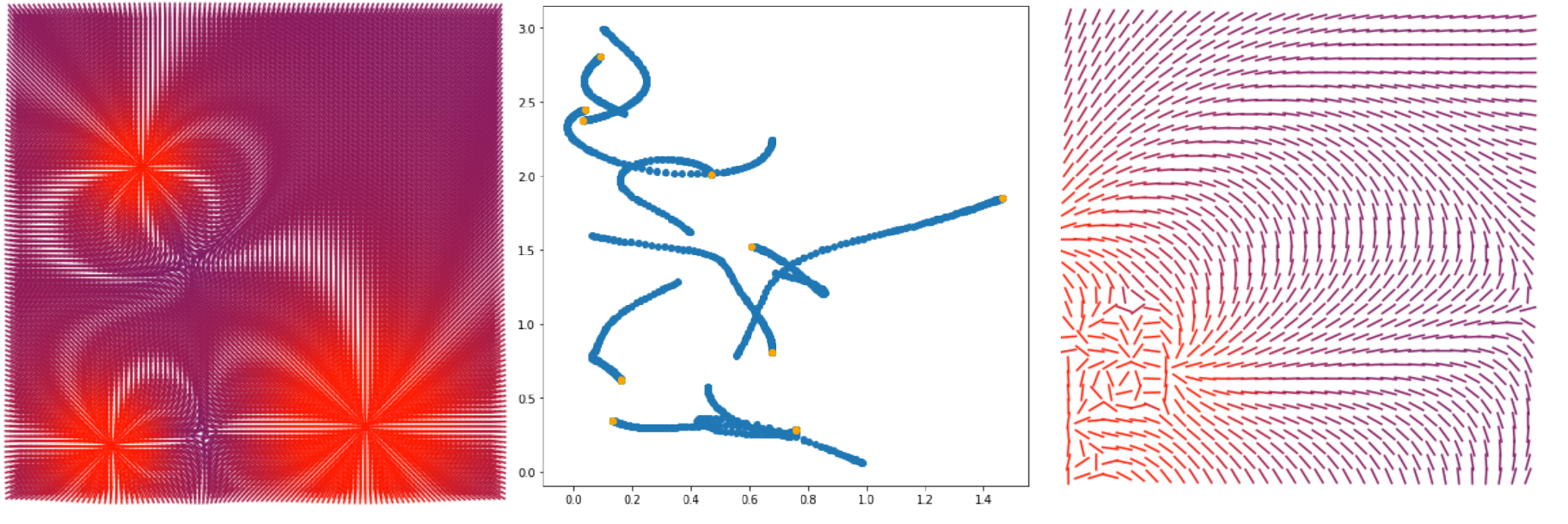
Que se passera-t-il dans cet article.

Cas général:

Nous décrivons la base, à savoir, travailler avec des vecteurs (un vélo pour ceux qui n'ont pas de numpy sous la main)
Nous décrivons le point matériel et le champ d'interaction

Cas particulier (basé sur général):

Faisons une visualisation du champ vectoriel de l'intensité du champ électromagnétique (première et troisième images)
Nous allons visualiser le mouvement des particules dans un champ électromagnétique

Rencontrez-moi sous la coupe!

Programmation théorique de base

Vecteur

La base de toutes les fondations est un vecteur (surtout dans notre cas). C'est donc avec la description du vecteur que nous allons commencer. De quoi avons-nous besoin? Opérations arithmétiques sur un vecteur, une distance, un module et quelques éléments techniques. Le vecteur dont nous hériterons de la liste. Voici à quoi ressemble son initialisation:

class Vector(list): def __init__(self, *el): for e in el: self.append(e)

Autrement dit, maintenant nous pouvons créer un vecteur avec

 v = Vector(1, 2, 3)

Définissons l'addition de l'opération arithmétique:

 class Vector(list): ... def __add__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] + other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self + other

Super:

 v1 = Vector(1, 2, 3) v2 = Vector(2, 57, 23.2) v1 + v2 >>> [3, 59, 26.2]

Nous définissons également toutes les opérations arithmétiques (le code complet du vecteur sera inférieur). Maintenant, vous avez besoin de la fonction de distance. Je pourrais faire une dist rustique (v1, v2) - mais ce n'est pas beau, alors redéfinissez l'opérateur%:

 class Vector(list): ... def __mod__(self, other): return sum((self - other) ** 2) ** 0.5

Super:

 v1 = Vector(1, 2, 3) v2 = Vector(2, 57, 23.2) v1 % v2 >>> 58.60068258988115

Nous avons également besoin de quelques méthodes pour une génération de vecteur plus rapide et une belle sortie. Il n'y a rien de compliqué ici, alors voici le code entier de la classe Vector:

Tous les codes de classe vectorielle

 class Vector(list): def __init__(self, *el): for e in el: self.append(e) def __add__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] + other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self + other def __sub__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] - other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self - other def __mul__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] * other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self * other def __truediv__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] / other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self / other def __pow__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] ** other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self ** other def __mod__(self, other): return sum((self - other) ** 2) ** 0.5 def mod(self): return self % Vector.emptyvec(len(self)) def dim(self): return len(self) def __str__(self): if len(self) == 0: return "Empty" r = [str(i) for i in self] return "< " + " ".join(r) + " >" def _ipython_display_(self): print(str(self)) @staticmethod def emptyvec(lens=2, n=0): return Vector(*[n for i in range(lens)]) @staticmethod def randvec(dim): return Vector(*[random.random() for i in range(dim)])

Point matériel

Ici, en théorie, tout est simple - le point a des coordonnées, de la vitesse et de l'accélération (pour plus de simplicité). De plus, elle a une masse et un ensemble de paramètres personnalisés (par exemple, pour un champ électromagnétique, une charge ne nous fait pas de mal, mais personne ne vous dérange pour régler au moins un spin).

L'initialisation sera la suivante:

 class Point: def __init__(self, coords, mass=1.0, q=1.0 speed=None, **properties): self.coords = coords if speed is None: self.speed = Vector(*[0 for i in range(len(coords))]) else: self.speed = speed self.acc = Vector(*[0 for i in range(len(coords))]) self.mass = mass self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys()) self.q = q for prop in properties: setattr(self, prop, properties[prop])

Et pour déplacer, immobiliser et accélérer notre propos, nous écrirons les méthodes suivantes:

 class Point: ... def move(self, dt): self.coords = self.coords + self.speed * dt def accelerate(self, dt): self.speed = self.speed + self.acc * dt def accinc(self, force): #        self.acc = self.acc + force / self.mass def clean_acc(self): self.acc = self.acc * 0

Bien joué, le point lui-même est fait.

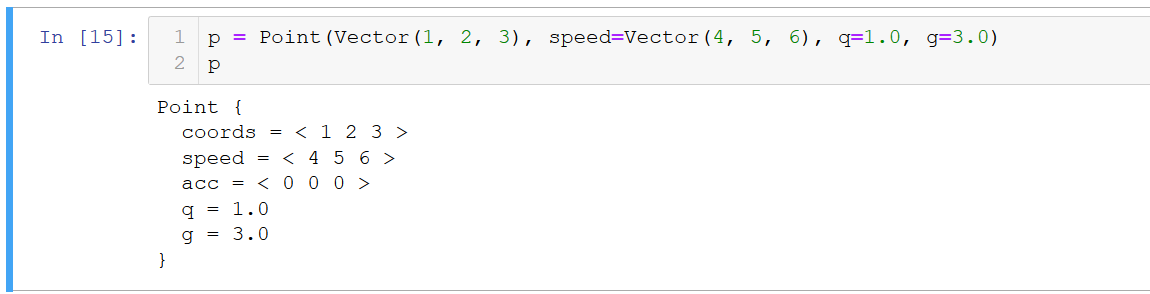
Code de point (avec une belle sortie)

 class Point: def __init__(self, coords, mass=1.0, q=1.0 speed=None, **properties): self.coords = coords if speed is None: self.speed = Vector(*[0 for i in range(len(coords))]) else: self.speed = speed self.acc = Vector(*[0 for i in range(len(coords))]) self.mass = mass self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys()) self.q = q for prop in properties: setattr(self, prop, properties[prop]) def move(self, dt): self.coords = self.coords + self.speed * dt def accelerate(self, dt): self.speed = self.speed + self.acc * dt def accinc(self, force): self.acc = self.acc + force / self.mass def clean_acc(self): self.acc = self.acc * 0 def __str__(self): r = ["Point {"] for p in self.__params__: r.append(" " + p + " = " + str(getattr(self, p))) r += ["}"] return "\n".join(r) def _ipython_display_(self): print(str(self))

Résultat:

Champ d'interaction

Nous appelons le champ d'interaction un objet qui comprend l'ensemble de tous les points matériels et exerce une force sur eux. Nous considérerons un cas particulier de notre merveilleux univers, nous aurons donc une interaction personnalisée (bien sûr, c'est facile à développer). Déclarez un constructeur et ajoutez un point:

 class InteractionField: def __init__(self, F): # F -   , F(p1, p2, r), p1, p2 - , r -    self.points = [] self.F = F def append(self, *args, **kwargs): self.points.append(Point(*args, **kwargs))

Maintenant, la partie amusante consiste à déclarer une fonction qui renvoie la «tension» à ce point. Bien que ce concept se réfère à l'interaction électromagnétique, dans notre cas, c'est un vecteur abstrait le long duquel nous déplacerons le point. Dans ce cas, nous aurons la propriété du point q, dans le cas particulier - la charge du point (en général - tout ce que nous voulons, même le vecteur). Alors, quelle est la tension au point C? Quelque chose comme ça:

v e c E (v e c C) = s u m v e c F_{i} (v e c C)

$\ vec E (\ vec C) = \ sum {\ vec F_i (\ vec C)}$

Autrement dit, la tension au point

v e c C

$\ vec C$ égal à la somme des forces de tous les points matériels agissant sur un point unitaire.

 class InteractionField: ... def intensity(self, coord): proj = Vector(*[0 for i in range(coord.dim())]) single_point = Point(Vector(), mass=1.0, q=1.0) #       (   ,       F,      ) for p in self.points: if coord % p.coords < 10 ** (-10): #      ,        ,   ,     (  ) continue d = p.coords % coord fmod = self.F(single_point, p, d) * (-1) #    -  proj = proj + (coord - p.coords) / d * fmod #  return proj

À ce stade, vous pouvez déjà dessiner un champ vectoriel, mais nous le ferons à la fin. Maintenant, faisons un pas dans notre interaction

 class InteractionField: ... def step(self, dt): self.clean_acc() for p in self.points: p.accinc(self.intensity(p.coords) * pq) p.accelerate(dt) p.move(dt)

Ici, tout est simple. Pour chaque point, nous déterminons la tension dans ces coordonnées, puis déterminons la force finale sur le point matériel ETU:

v e c F = v e c E * q

$\ vec F = \ vec E * q$

Définissez les fonctions manquantes.

Tous les codes InteractionField

 class InteractionField: def __init__(self, F): self.points = [] self.F = F def move_all(self, dt): for p in self.points: p.move(dt) def intensity(self, coord): proj = Vector(*[0 for i in range(coord.dim())]) single_point = Point(Vector(), mass=1.0, q=1.0) for p in self.points: if coord % p.coords < 10 ** (-10): continue d = p.coords % coord fmod = self.F(single_point, p, d) * (-1) proj = proj + (coord - p.coords) / d * fmod return proj def step(self, dt): self.clean_acc() for p in self.points: p.accinc(self.intensity(p.coords) * pq) p.accelerate(dt) p.move(dt) def clean_acc(self): for p in self.points: p.clean_acc() def append(self, *args, **kwargs): self.points.append(Point(*args, **kwargs)) def gather_coords(self): return [p.coords for p in self.points]

Un cas particulier. Mouvement des particules et visualisation du champ vectoriel

Nous sommes donc arrivés au plus intéressant. Commençons par ...

Modélisation du mouvement des particules dans un champ électromagnétique

 u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 2 + 0.1)) for i in range(3): u.append(Vector.randvec(2) * 10, q=random.random() - 0.5)

En fait, le coefficient k devrait être égal à une sorte de milliards (9 * 10 ^ (- 9)), mais comme il sera éteint au moment t -> 0, j'ai immédiatement décidé de faire des deux des nombres adéquats. Par conséquent, dans notre physique k = 300'000. Et avec tout le reste, je pense que c'est clair.

r ** 2 + 0,1

- c'est éviter de diviser par 0. Nous pourrions, bien sûr, être confus, résoudre un grand système de diffours, mais d'une part il n'y a pas d'équation de mouvement pour plus de 2 corps, et d'autre part cela n'est clairement pas inclus dans le concept d '«article pour débutants»

Ensuite, nous ajoutons dix points (espace bidimensionnel) avec des coordonnées de 0 à 10 le long de chaque axe. De plus, nous donnons à chaque point une charge de -0,25 à 0,25. Faites maintenant une boucle et dessinez des points en fonction de leurs coordonnées (et traces):

 X, Y = [], [] for i in range(130): u.step(0.0006) xd, yd = zip(*u.gather_coords()) X.extend(xd) Y.extend(yd) plt.figure(figsize=[8, 8]) plt.scatter(X, Y) plt.scatter(*zip(*u.gather_coords()), color="orange") plt.show()

Ce qui aurait dû arriver:

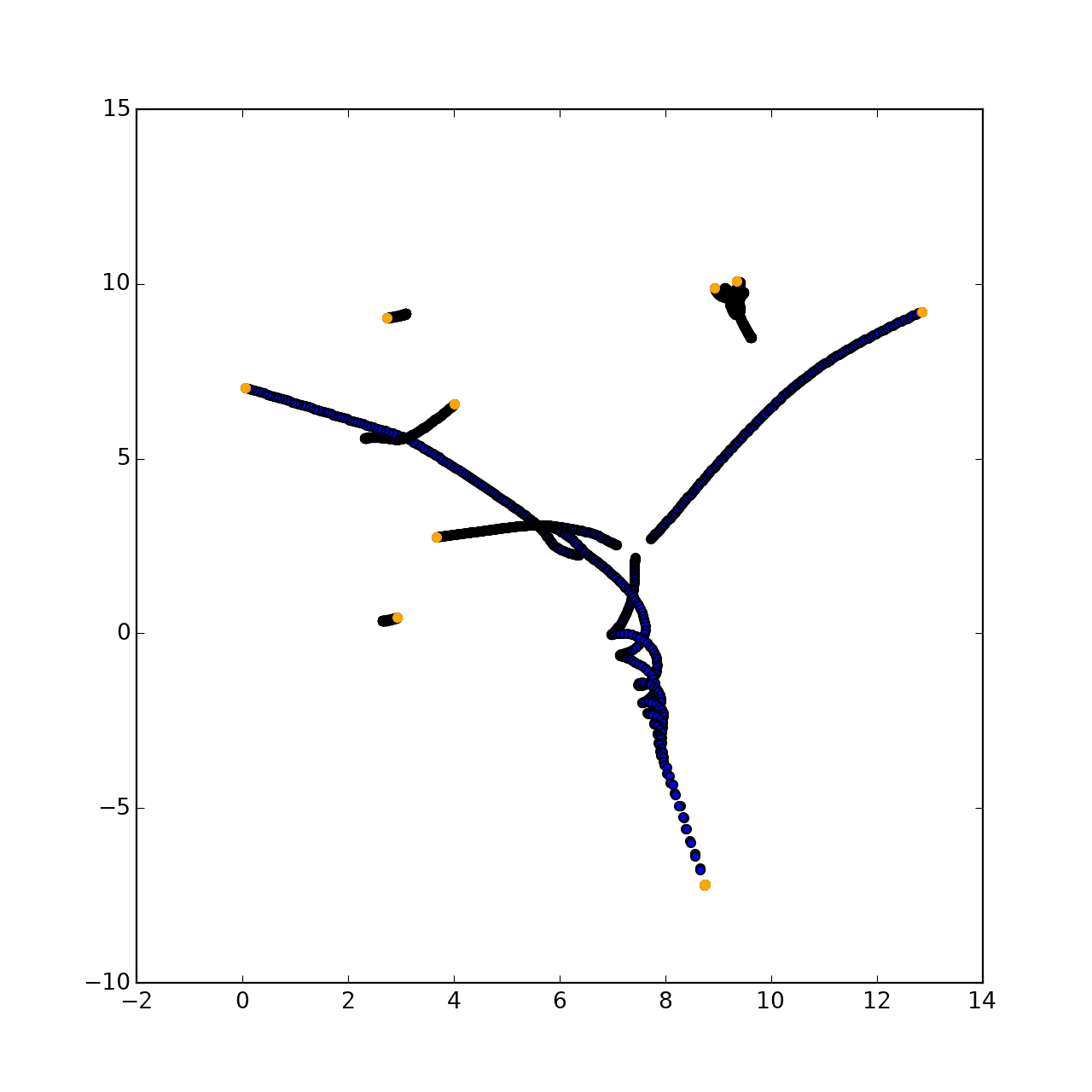
En fait, le dessin y sera complètement aléatoire, car la trajectoire de chaque point est imprévisible au moment du développement de la mécanique.

Visualisation de champ vectoriel

Ici, tout est simple. Nous devons parcourir les coordonnées avec un certain pas et dessiner un vecteur dans chacun d'eux dans la bonne direction.

 fig = plt.figure(figsize=[5, 5]) res = [] STEP = 0.3 for x in np.arange(0, 10, STEP): for y in np.arange(0, 10, STEP): inten = u.intensity(Vector(x, y)) F = inten.mod() inten /= inten.mod() * 4 #     res.append(([x - inten[0] / 2, x + inten[0] / 2], [y - inten[1] / 2, y + inten[1] / 2], F)) for r in res: plt.plot(r[0], r[1], color=(sigm(r[2]), 0.1, 0.8 * (1 - sigm(r[2])))) #        plt.show()

Environ cette conclusion aurait dû être obtenue.

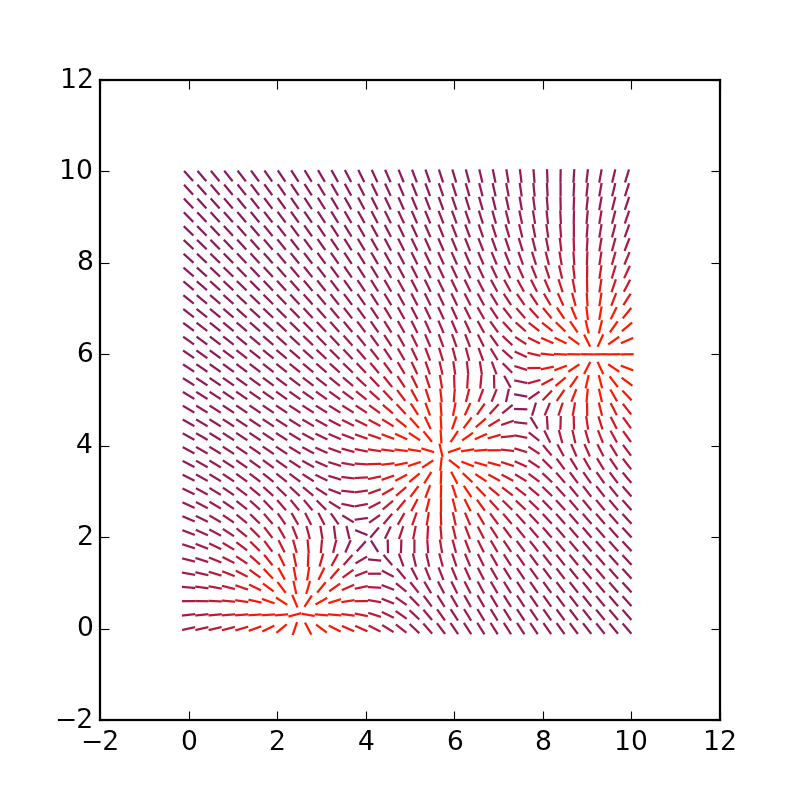
Vous pouvez allonger les vecteurs eux-mêmes, remplacer * 4 par * 1.5:

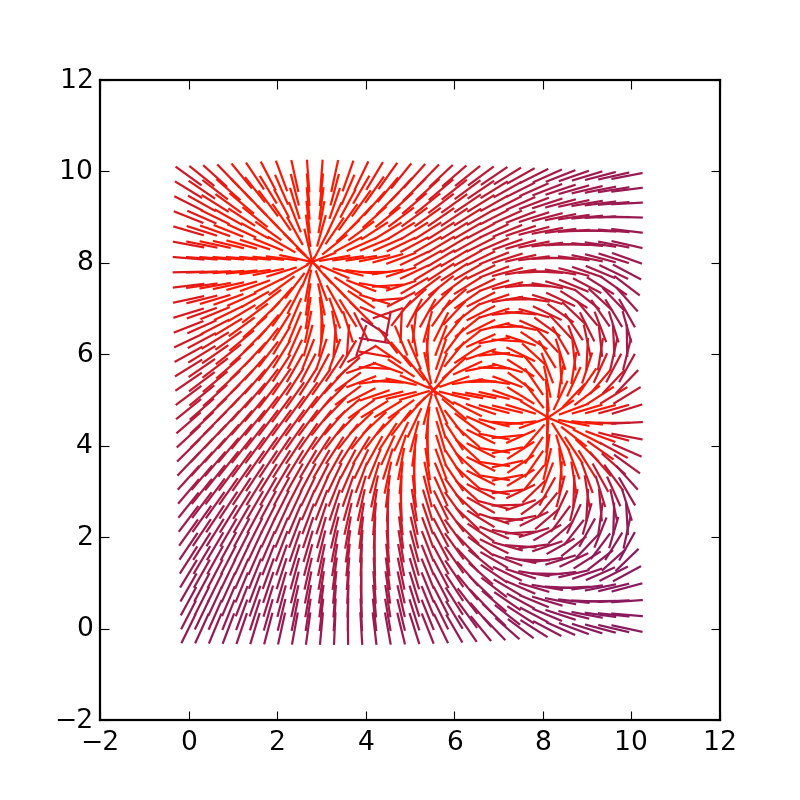
Nous jouons avec la dimensionnalité et la modélisation

Créez un espace à cinq dimensions avec 200 points et une interaction qui ne dépend pas du carré de la distance, mais du 4e degré.

 u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 4 + 0.1)) for i in range(200): u.append(Vector.randvec(5) * 10, q=random.random() - 0.5)

Désormais, toutes les coordonnées, vitesses, etc. sont définies en cinq dimensions. Maintenant, modélisons quelque chose:

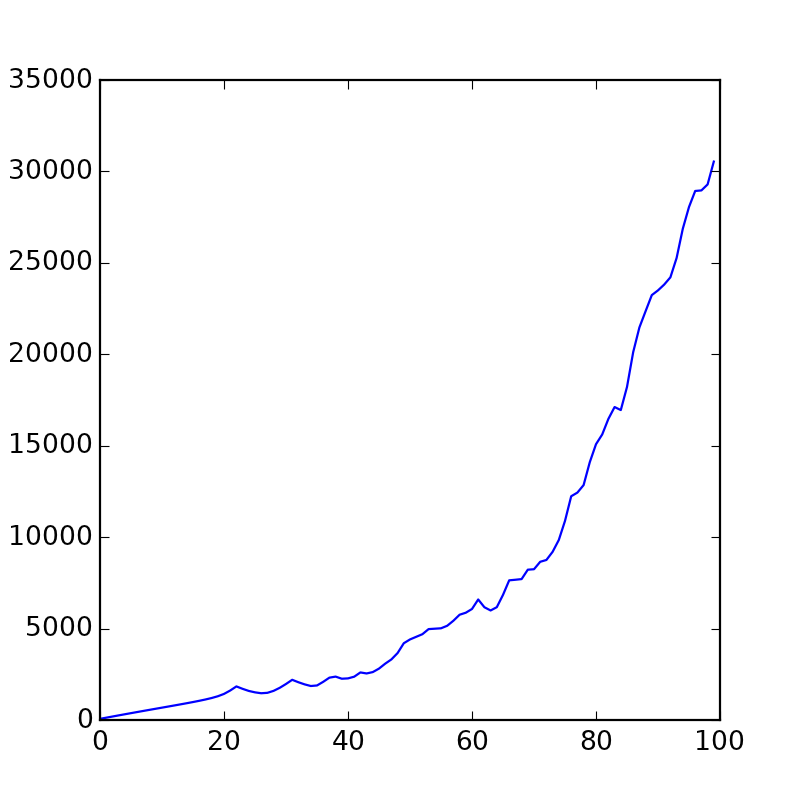
 velmod = 0 velocities = [] for i in range(100): u.step(0.0005) velmod = sum([p.speed.mod() for p in u.points]) #       velocities.append(velmod) plt.plot(velocities) plt.show()

Il s'agit d'un graphique de la somme de toutes les vitesses à un moment donné. Comme vous pouvez le voir, au fil du temps, ils accélèrent lentement.

Eh bien, c'était une courte instruction sur la façon de faire une chose aussi simple. Mais que se passe-t-il si vous jouez avec des fleurs:

Tout le code avec démo

 import random class Vector(list): def __init__(self, *el): for e in el: self.append(e) def __add__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] + other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self + other def __sub__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] - other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self - other def __mul__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] * other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self * other def __truediv__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] / other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self / other def __pow__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] ** other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self ** other def __mod__(self, other): return sum((self - other) ** 2) ** 0.5 def mod(self): return self % Vector.emptyvec(len(self)) def dim(self): return len(self) def __str__(self): if len(self) == 0: return "Empty" r = [str(i) for i in self] return "< " + " ".join(r) + " >" def _ipython_display_(self): print(str(self)) @staticmethod def emptyvec(lens=2, n=0): return Vector(*[n for i in range(lens)]) @staticmethod def randvec(dim): return Vector(*[random.random() for i in range(dim)]) class Point: def __init__(self, coords, mass=1.0, q=1.0, speed=None, **properties): self.coords = coords if speed is None: self.speed = Vector(*[0 for i in range(len(coords))]) else: self.speed = speed self.acc = Vector(*[0 for i in range(len(coords))]) self.mass = mass self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys()) self.q = q for prop in properties: setattr(self, prop, properties[prop]) def move(self, dt): self.coords = self.coords + self.speed * dt def accelerate(self, dt): self.speed = self.speed + self.acc * dt def accinc(self, force): self.acc = self.acc + force / self.mass def clean_acc(self): self.acc = self.acc * 0 def __str__(self): r = ["Point {"] for p in self.__params__: r.append(" " + p + " = " + str(getattr(self, p))) r += ["}"] return "\n".join(r) def _ipython_display_(self): print(str(self)) class InteractionField: def __init__(self, F): self.points = [] self.F = F def move_all(self, dt): for p in self.points: p.move(dt) def intensity(self, coord): proj = Vector(*[0 for i in range(coord.dim())]) single_point = Point(Vector(), mass=1.0, q=1.0) for p in self.points: if coord % p.coords < 10 ** (-10): continue d = p.coords % coord fmod = self.F(single_point, p, d) * (-1) proj = proj + (coord - p.coords) / d * fmod return proj def step(self, dt): self.clean_acc() for p in self.points: p.accinc(self.intensity(p.coords) * pq) p.accelerate(dt) p.move(dt) def clean_acc(self): for p in self.points: p.clean_acc() def append(self, *args, **kwargs): self.points.append(Point(*args, **kwargs)) def gather_coords(self): return [p.coords for p in self.points] #  import matplotlib.pyplot as plt import numpy as np import time #     if False: u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 2 + 0.1)) for i in range(10): u.append(Vector.randvec(2) * 10, q=(random.random() - 0.5) / 2) X, Y = [], [] for i in range(130): u.step(0.0006) xd, yd = zip(*u.gather_coords()) X.extend(xd) Y.extend(yd) plt.figure(figsize=[8, 8]) plt.scatter(X, Y) plt.scatter(*zip(*u.gather_coords()), color="orange") plt.show() def sigm(x): return 1 / (1 + 1.10 ** (-x/1000)) #    if False: u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 2 + 0.1)) for i in range(3): u.append(Vector.randvec(2) * 10, q=random.random() - 0.5) fig = plt.figure(figsize=[5, 5]) res = [] STEP = 0.3 for x in np.arange(0, 10, STEP): for y in np.arange(0, 10, STEP): inten = u.intensity(Vector(x, y)) F = inten.mod() inten /= inten.mod() * 1.5 res.append(([x - inten[0] / 2, x + inten[0] / 2], [y - inten[1] / 2, y + inten[1] / 2], F)) for r in res: plt.plot(r[0], r[1], color=(sigm(r[2]), 0.1, 0.8 * (1 - sigm(r[2])))) plt.show() #    5-  if False: u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 4 + 0.1)) for i in range(200): u.append(Vector.randvec(5) * 10, q=random.random() - 0.5) velmod = 0 velocities = [] for i in range(100): u.step(0.0005) velmod = sum([p.speed.mod() for p in u.points]) velocities.append(velmod) plt.plot(velocities) plt.show()

Le prochain article portera probablement sur une modélisation plus complexe, et peut-être sur les fluides et les équations de Navier-Stokes.
UPD: Un article écrit par mon collègue ici

Merci à MomoDev d' avoir aidé à rendre la vidéo.

Simulation élémentaire d'interaction physique personnalisée en python + matplotlib