Et pourtant, pourquoi Posit est une alternative valable à IEEE 754

Le mois de la position sur Habré a été déclaré ouvert, ce qui signifie que je ne peux pas passer outre et ignorer les critiques qui leur sont adressées. Dans la série précédente:

Une nouvelle approche peut nous aider à nous débarrasser des calculs en virgule flottante
Posit-arithmétique: vaincre un point flottant dans son propre champ. Partie 1
Posit-arithmétique: vaincre un point flottant dans son propre champ. 2e partie
Défis posés par les adultes

Je pense que beaucoup d'entre vous se souviennent immédiatement d'au moins un cas de l'histoire où les idées révolutionnaires au moment de leur formation ont été rejetées par une communauté d'experts. En règle générale, la faute d'un tel comportement est le vaste bagage de connaissances déjà accumulées qui ne permet pas de regarder l'ancien problème sous un nouveau jour. Ainsi, la nouvelle idée perd en termes de caractéristiques par rapport aux approches établies, car elle n'est évaluée que par les paramètres jugés importants au stade de développement précédent.

C'est précisément le type d'aversion auquel le format Posit est confronté aujourd'hui: les critiques se contentent souvent de «regarder dans la mauvaise direction» et utilisent même la Posit dans leurs expériences de la mauvaise manière. Dans cet article, je vais essayer d'expliquer pourquoi.

Les avantages de Posit ont déjà été assez mentionnés: élégance mathématique, grande précision sur les valeurs à faible exposant, large éventail de valeurs, une seule représentation binaire de NaN et zéro, absence de valeurs subnormales, lutte contre les débordements / débordements. Beaucoup de critiques ont été exprimées: une précision inutile pour des valeurs très grandes ou très petites, un format de représentation binaire complexe et, bien sûr, un manque de support matériel.

Je ne veux pas répéter les arguments que j'ai déjà mentionnés; je vais plutôt essayer de me concentrer sur l'aspect qui, en règle générale, est négligé.

Les règles du jeu ont changé

La norme IEEE 754 décrit les nombres à virgule flottante implémentés dans Intel 8087 il y a près de 40 ans. Selon les normes de notre industrie, c'est un moment incroyable; tout a changé depuis: les performances du processeur, le coût de la mémoire, les volumes de données et l'échelle des calculs. Le format Posit a été développé non seulement comme la meilleure version de l'IEEE 754, mais comme une approche pour travailler avec des nombres qui répond aux nouvelles exigences de l'époque.

La tâche de haut niveau est restée la même - nous avons tous besoin de calculs efficaces dans le domaine des nombres rationnels avec une perte de précision minimale. Mais les conditions dans lesquelles la tâche est résolue sont radicalement modifiées.

Premièrement, les priorités d'optimisation ont changé. Il y a 40 ans, les performances des ordinateurs dépendaient presque entièrement des performances des processeurs. Aujourd'hui, les performances de la plupart des ordinateurs reposent sur la mémoire. Pour vérifier cela, il suffit de regarder les principaux domaines de développement des processeurs des dernières décennies: la mise en cache à trois niveaux, l'exécution spéculative, le pipelining des calculs, la prédiction de branche. Toutes ces approches visent à atteindre des performances élevées dans des conditions de calcul rapide et d'accès lent à la mémoire.



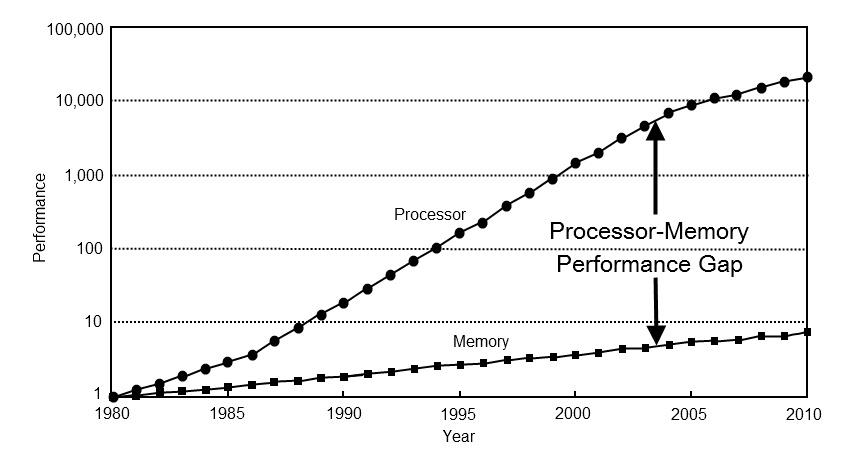
Deuxièmement, une nouvelle exigence est apparue: la consommation effective d'énergie. Au cours des dernières décennies, la technologie de mise à l'échelle horizontale de l'informatique a tellement progressé que nous avons commencé à nous préoccuper moins de la vitesse de ces calculs, mais de la facture d'électricité. Ici, je dois souligner une partie importante à comprendre. Du point de vue de l'efficacité énergétique, les calculs sont bon marché, car les registres du processeur sont très proches de ses ordinateurs. Il sera beaucoup plus cher de payer pour le transfert de données, à la fois entre le processeur et la mémoire (x100), et sur de longues distances (x1000 ...).



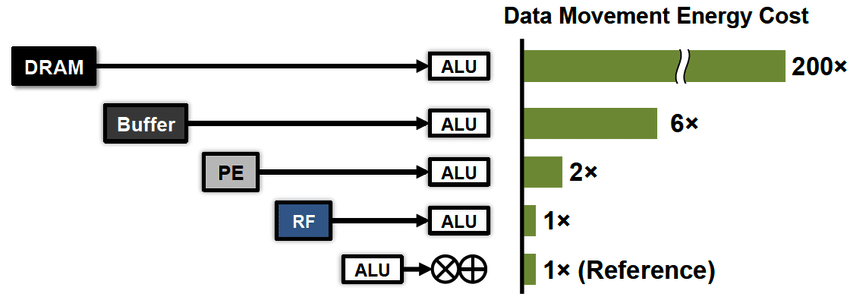
Voici un exemple de projet scientifique que Posit prévoit d'utiliser:



Ce réseau de télescopes génère 200 pétaoctets de données par seconde, dont le traitement prend la puissance d'une petite centrale électrique - 10 mégawatts . De toute évidence, pour de tels projets, la réduction des données et de la consommation d'énergie est critique.

Au tout début

Alors, que propose la norme Posit? Pour comprendre cela, vous devez revenir au tout début de la discussion et comprendre ce que signifie la précision des nombres à virgule flottante.

Il y a en fait deux aspects différents liés à la précision. Le premier aspect est la précision des calculs - dans quelle mesure les résultats des calculs s'écartent pendant diverses opérations. Le deuxième aspect est la précision de la présentation - à quel point la valeur d'origine est déformée au moment de la conversion du champ des nombres rationnels au champ des nombres à virgule flottante d'un format particulier.

Maintenant, il y aura un moment important de sensibilisation. La position est principalement un format pour représenter des nombres rationnels, pas un moyen d'effectuer des opérations sur eux. En d'autres termes, Posit est un format de compression rationnel avec perte. Vous avez peut-être entendu l'affirmation selon laquelle la position 32 bits est une bonne alternative au flottant 64 bits. Nous parlons donc de diviser par deux précisément la quantité de données requise pour stocker et transmettre le même ensemble de chiffres. Deux fois moins de mémoire - près de 2 fois moins de consommation d'énergie et des performances élevées du processeur en raison des attentes plus faibles d'accès à la mémoire.

Deuxième extrémité du bâton

Ici, vous devriez avoir une question logique: quel est l'intérêt de représenter efficacement des nombres rationnels s'il ne permet pas d'effectuer des calculs avec une grande précision.

En fait, il existe un moyen de faire des calculs exacts, et cela s'appelle Quire. Il s'agit d'un autre format de représentation des nombres rationnels, inextricablement lié à Posit. Contrairement à Posit, le format Quire est conçu spécifiquement pour les calculs et pour le stockage des valeurs intermédiaires dans les registres, et non dans la mémoire principale.



En bref, le Quire n'est rien de plus qu'une large batterie entière (arithmétique à virgule fixe). L'unité, en tant que représentation binaire de Quire, correspond à la valeur positive minimale de Posit. La valeur Quire maximale correspond à la valeur Posit maximale. Chaque valeur Posit a une représentation unique dans Quire sans perte de précision, mais toutes les valeurs Quire ne peuvent pas être représentées dans Posit sans perte de précision.

Les avantages de Quire sont évidents. Ils vous permettent d'effectuer des opérations avec une précision incomparablement plus élevée que Float, et pour les opérations d'addition et de multiplication, il n'y aura aucune perte de précision. Le prix à payer est de larges registres de processeur (Posit 32 bits avec es = 2 correspond à Quire 512 bits), mais ce n'est pas un problème sérieux pour les processeurs modernes. Et si, il y a 40 ans, le calcul de plus de 512 bits entiers semblait un luxe inacceptable, c'est aujourd'hui plutôt une alternative adéquate au large accès à la mémoire.

Assembler le puzzle

Ainsi, Posit offre non seulement une nouvelle norme sous la forme d'une alternative à Float / Double, mais plutôt une nouvelle approche pour travailler avec les nombres. Contrairement à Float - qui est une représentation unique essayant de trouver un compromis entre précision et efficacité de stockage et efficacité de calcul, Posit propose deux formats de présentation différents, l'un pour le stockage et la transmission des nombres - Posit lui-même, et l'autre pour les calculs et leur intermédiaire Valeurs - Quire.

Lorsque nous résolvons des problèmes pratiques en utilisant des nombres à virgule flottante, du point de vue du processeur, travailler avec eux peut être représenté comme un ensemble des actions suivantes:

1. Lisez les valeurs des nombres de la mémoire.
2. Effectuez une séquence d'opérations. Parfois, le nombre d'opérations est assez important. Dans ce cas, toutes les valeurs intermédiaires des calculs sont stockées dans des registres.
3. Écrivez le résultat des opérations dans la mémoire.

Avec Float / Double, la précision est perdue à chaque opération. Avec Posit + Quire, la perte de précision lors du calcul est négligeable. Elle n'est perdue qu'à la dernière étape, au moment de la conversion de la valeur Quire en Posit. C'est pourquoi la plupart des problèmes «d'accumulation d'erreurs» pour Posit + Quire ne sont tout simplement pas pertinents.

Contrairement à Float / Double, lorsque vous utilisez Posit + Quire, nous pouvons généralement offrir une représentation plus compacte des nombres. Résultat: un accès plus rapide aux données de la mémoire (meilleures performances) et un stockage et une transmission des informations plus efficaces.

Ratio de Mueller

À titre de démonstration visuelle, je ne donnerai qu'un exemple - la relation de récurrence classique de Muller, inventée spécifiquement pour démontrer comment l'accumulation d'erreurs dans les calculs en virgule flottante déforme radicalement le résultat des calculs.



Dans le cas de l'utilisation de l'arithmétique avec une précision arbitraire, la séquence de récurrence doit être réduite à la valeur 5. Dans le cas de l'arithmétique à virgule flottante, la question est uniquement de savoir sur quelle itération les résultats du calcul commenceront à avoir une déviation insuffisante.

J'ai mené une expérience pour IEEE 754 avec une précision simple et double, ainsi que pour Posit + Quire 32 bits. Les calculs ont été effectués en arithmétique Quire, mais chaque valeur du tableau a été convertie en Posit.


Comme vous pouvez le voir dans le tableau, Float 32 bits se rend déjà à la septième valeur et Float 64 bits a duré jusqu'à la 14e itération. Dans le même temps, les calculs de Posit utilisant Quire donnent un résultat stable jusqu'à 58 itérations!

Moral

Pour de nombreux cas pratiques, et s'il est utilisé correctement, le format Posit vous permettra vraiment d'économiser de la mémoire d'une part, en compressant les nombres mieux que Float, et d'autre part fournir une meilleure précision de calcul grâce à Quire.

Mais ce n'est qu'une théorie! Quand il s'agit de précision ou de performance, faites toujours des tests avant de faire confiance aveuglément à une approche ou à une autre. En effet, dans la pratique, votre cas particulier se révélera exceptionnel beaucoup plus souvent qu'en théorie.

Eh bien, n'oubliez pas la première loi de Clark (interprétation gratuite): lorsqu'un expert respecté et expérimenté prétend qu'une nouvelle idée fonctionnera, il a presque certainement raison. Quand il prétend que la nouvelle idée ne fonctionnera pas, alors il est très probable qu'il se trompe. Je ne me considère pas comme un expert expérimenté pour vous permettre de vous fier à mon opinion, mais je vous demande de vous méfier de critiquer même des personnes expérimentées et respectées. Après tout, le diable est dans les détails, et même les personnes expérimentées peuvent les manquer.